2. 中国空气动力研究与发展中心, 四川 绵阳 621000
2. China Aerodynamics Research and Development Center, Mianyang Sichuan 621000, China
为了提高作战半径及突防能力,先进飞行器往往把高速与隐身作为其重要技战指标,而为了实现上述指标,飞行器所携带的武器通常会采用内埋式装载方式,如美国的F-22/F-35、俄罗斯的T-50以及中国的歼-20等均采用了内埋式武器装载方式。武器内埋式装载在带来显著收益的同时也引发了许多新的空气动力学/气动声学问题:如舱门开启或武器投放瞬间可能产生较大的动态冲击载荷;某些几何布局的弹舱压力梯度较大,武器分离时存在机/弹相互碰撞的危险;舱门开启后,武器舱内部及周围产生强烈的气动噪声,可引发结构振动并造成结构疲劳;处于复杂流场且快速运动的武器舱舱门可能发生振动及变形,严重时甚至存在舱门被撕裂或吹飞的危险。
自20世纪50年代以来,内埋武器舱系统引发的复杂流动[1-2]、气动声学[3-4]以及武器分离安全性[5-6]等问题一直是空气动力学界研究的热点。美国国家航空航天局以及阿诺德工程发展中心两家单位对内埋武器舱系统进行了系统而深入的研究,为F-22/F-35战斗机内埋武器舱关键气动及声学问题的解决提供了有力的技术支持,但涉及到高度机密,其公开发表的文献很少。为改善内埋武器舱系统的气动特性,国外学者进行了多种流动控制方法研究[7-9],但从公开发表的文献看,利用多种试验手段进行综合研究的文献很少。
国内在内埋武器舱系统方面研究起步较晚,相关的试验设备及技术尚不完备,目前仅开展了少量的试验研究[10-12],研究的深度及广度都有待进一步深入。本文以静压测量、脉动压力测量以及网格测力等手段,对弹舱流场稳态压力分布特性、气动声学特性以及内埋武器分离特性等进行了分析,同时研究了在弹舱前缘施以流动控制对上述特性的影响。
1 风洞及试验模型 1.1 试验风洞在中国空气动力研究与发展中心高速所FL-21风洞进行本项试验研究,FL-21风洞为亚跨超三声速风洞,试验段开口尺寸为0.6m×0.6m,试验段长度为1.775m,马赫数范围为0.4~3.5。
1.2 弹舱模型弹舱模型安装在矩形平板上,试验模型整体安装于试验段侧壁,图 1为试验模型安装于风洞中的照片。

|
| 图 1 试验模型照片 Fig. 1 Sketch of testing model |
风洞侧壁与平板上表面的间距为0.040m,弹舱长度(L)为0.267m、宽度(W)为0.104m,深度(D)可在0~0.06m范围内调节。弹舱底板沿中轴线上等间隔分布有27个脉动压力测点和26个静压测点,X/L表示弹舱底部上的相对位置,零点位于弹舱底板与前壁相交位置,顺气流方向为正。
1.3 武器模型图 2给出了武器模型简图。

|
| 图 2 武器模型 Fig. 2 Sketch of weapon model |
武器为细长体导弹模型,武器模型全长0.232m,等直段直径(d)为0.011m,武器分离平面距弹舱中轴面距离为0.015m。武器模型采用尾支撑方式,利用电机驱动机构带动武器模型在垂直方向上运动,利用5分量内式天平测量武器模型的气动力。以Zs/d表示武器模型与平板的相对距离,Zs为正时武器模型在舱外,为负时武器模型在舱内。
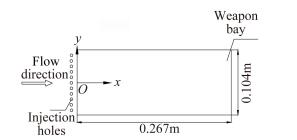
1.4 流动控制器件本文设计了一种主动控制措施——质量射流。在弹舱前缘0.006m处设计一排射流孔,共11个,射流孔直径为0.0025m,射流气源为高压氮气瓶,通过流量计测量射流流量,文中给出了射流流量为27.3kg/h条件下的部分试验结果。
|
| 图 3 流动控制器件 Fig. 3 Sketch of flow control model |
1.5 试验测量设备
静态压力传感器单通道采样频率为100Hz,量程为103kPa,精确度为±0.15%。动态压力传感器为8514-10型压阻式传感器,量程为10Psi,固有频率为200kHz,名义灵敏度为4.35×10-3mv/Pa.。武器模型的力和力矩采用气动中心高速所研制的2N5-6DC天平进行测量,测量不确定度为5‰。
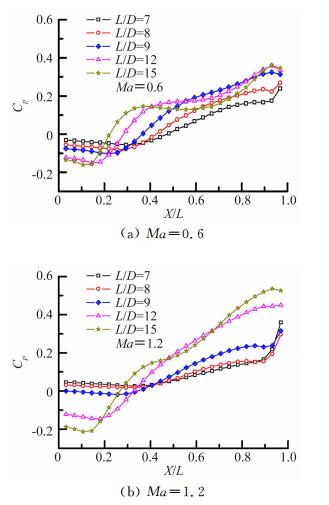
2 试验结果分析 2.1 弹舱流场稳态压力分布特性图 4给出了亚跨声速条件下,舱底稳态压力分布随弹舱长深比L/D变化。
|
| 图 4 舱底静压分布曲线 Fig. 4 Static pressure distributions of cavity floor |
图 4表明,弹舱长深比变化均对舱底稳态压力分布影响明显,随L/D增大,外流向舱内扩张的幅度逐渐增强,当弹舱长深比大于某一值时,气流不仅进入弹舱并且在弹舱底部形成附着区域,在到达弹舱后壁之前气流向舱外分离并向弹舱后方流动。随弹舱长深比增大,舱底稳态压力分布变化规律为,当L/D较小时,弹舱中前段压力分布较平直,量值在0附近,后段压力由于气流撞击及压缩增大,随L/D增大,气流在弹舱前缘向舱内扩张趋势增大,舱底前壁附近稳态压力逐渐降低,气流在弹舱后壁附近撞击及压缩强度增大,弹舱后部稳态压力进一步升高,当L/D达到某一值时,气流开始撞击弹舱底部并形成附着区,位于弹舱中段的稳态压力曲线上开始一个近似平台区,舱底前壁附近稳态压力达到最小值,之后,随L/D进一步增大,弹舱前壁附近最小压力值以及弹舱后壁之前的最大压力均无明显变化,弹舱中部的近似压力平台区长度增大,且沿X/L增大方向,稳态压力有降低的趋势,理论上讲,如果舱底附着区域足够长,稳态压力应降低至0附近。
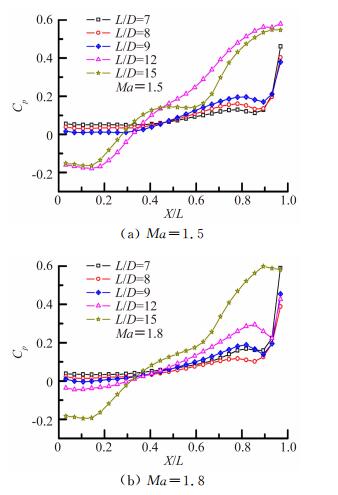
图 5给出了超声速条件下,舱底稳态压力分布随弹舱长深比L/D变化。
|
| 图 5 舱底静压分布曲线 Fig. 5 Static pressure distributions of cavity floor |
超声速时的情况略有不同,差异在于:随L/D增大过程中,舱底稳态压力梯度的增大不是逐渐增大的过程,而是一个突变的过程。如Ma=1.5时,L/D=9时舱底稳态压力梯度较小,对应流场类型为开式流动,而L/D=12时,流场类型对应为过渡/闭式流动,舱内稳态压力梯度大大升高,Ma=1.8时,L/D=12时舱底稳态压力梯度较小,对应流场类型为过渡/开式流动,而L/D=15时,流场类型对应为闭式流动。
通过上述分析可知:L/D变化对舱内稳态压力分布影响明显,该参数是决定弹舱流场类型主要参数;对应每个马赫数均可确定两个临界长深比(L/Dcr),当L/D<L/Dcr1时,随长深比减小,弹舱流场类型将保持为开式流动而不发生变化,而当L/D>L/Dcr2时,随长深比增大,弹舱流场类型均保持为闭式流动。
2.2 弹舱流场气动声学特性气动噪声本质上是由压力脉动产生的[13],因此本文利用动态压力数据对流场气动声学特性进行分析是合适的,文中给出了舱底总声压级分布以及X/L=0.99处的测点声压频谱曲线。
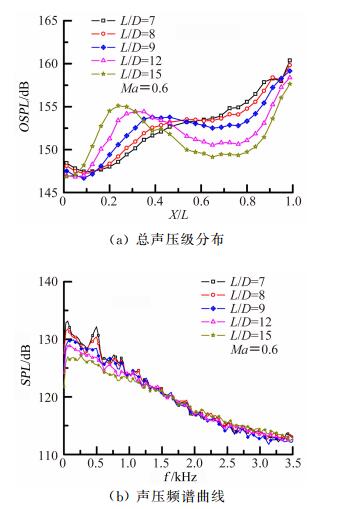
图 6为亚声速(Ma=0.6)时的试验结果。图中表明,随L/D减小,弹舱底部最大总声压级强度增大,声压频谱曲线上开始出现峰值单调声。从静压分布可知,该马赫数下,随L/D减小,弹舱流场类型从闭式流动向过渡式流动转变,对应闭式流动时(L/D=12、15),气流在舱底再附,阻碍声波前传,舱内不存在产生自持振荡的机制,舱内最大总声压级较小,声压频谱曲线上无能量尖峰。
|
| 图 6 气动声学特性曲线(Ma=0.6) Fig. 6 Curves of aero-acoustic characteristics(Ma=0.6) |
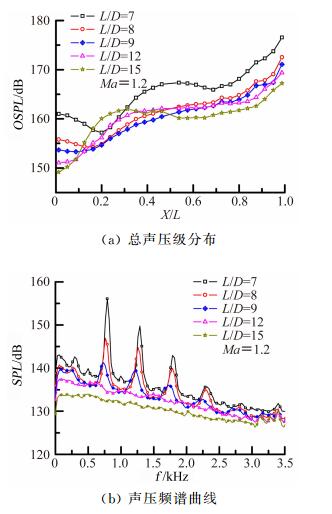
图 7为跨声速(Ma=1.2)时的试验结果。
|
| 图 7 气动声学特性曲线(Ma=1.2) Fig. 7 Curves of aero-acoustic characteristics(Ma=1.2) |
图 7表明,L/D减小过程中,典型测点声压频谱曲线上逐渐开始出现峰值单调声,随L/D减小,对应相同模态的峰值单调声幅值增大,但其对应频率基本不变,这与Rossiter半经验公式一致[14]。弹舱长深比L/D从15减小至7时,舱内最大总声压级增大近10dB,典型测点声压能量明显增大并出现了四处明显的峰值单调声,这显示弹舱流场形成了较强烈的自持振荡。
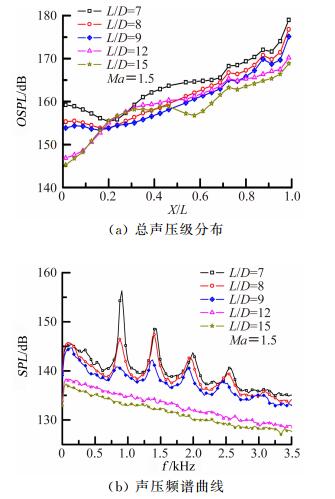
图 8为超声速(Ma=1.5)时的试验结果。
|
| 图 8 气动声学特性曲线(Ma=1.5) Fig. 8 Curves of aero-acoustic characteristics(Ma=1.5) |
图 8表明,Ma=1.5时,弹舱流场气动声学特性随L/D变化规律与Ma=1.2时的情况相似,在此不加赘述。
综上所述,相对闭式弹舱流场,开式弹舱流场气动声学环境较恶劣,舱内最大声压级可高出近10dB,且声压频谱曲线上存在多个明显的能量尖峰。笔者认为,对于开式弹舱流场,弹舱前缘的剪切层在形成初期包含有多种扰动因子,有多种尺度的白噪声扰动在涡卷起阶段被放大,放大的扰动有很宽的频谱,该阶段扰动因子对外部激励很敏感,在某一外在激励作用下,将存在一个功率谱峰值,其对应的频率fn可称之为弹舱自然频率,它与弹舱几何参数以及来流参数关系密切,此时扰动的动力学特性不是内禀的,流动本身将起到扰动放大器的作用,此后流动逐步为此优势模态所主导,并形成频率与弹舱自然频率一致的K-H涡,弹舱后壁可看成是噪声放大器,气流在该处撞击形成强烈的压力脉动,诱发产生强气动噪声的同时并产生声辐射,声辐射以一定频率向前传播,亚声速时其在整个空间流场内传播,超声速时在剪切层以及舱内向前传播,声辐射传播到弹舱前缘时将对剪切层产生激励,在该激励作用下,对应弹舱自然频率的扰动因子被放大,从而再次产生K-H涡,形成了自持振荡回路[15]。
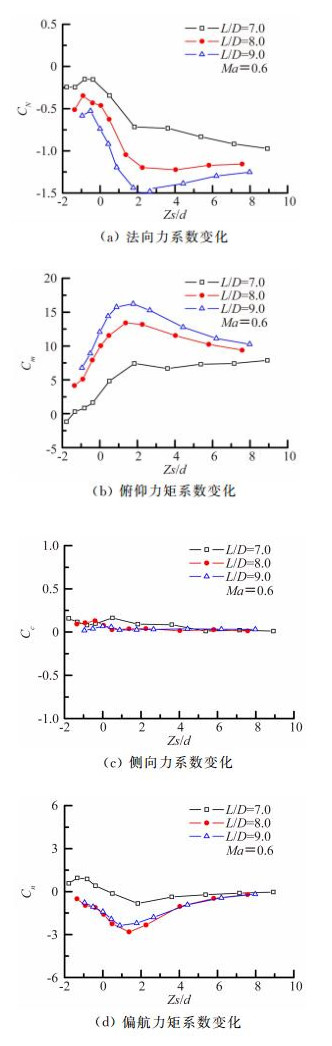
2.3 内埋武器分离气动力特性图 9给出了亚声速(Ma=0.6)时的试验结果。法向力系数(CN)及俯仰力矩系数(Cm)曲线表明,随L/D增大,曲线波动逐渐增大,最大俯仰力矩系数明显增加,这主要是因为L/D变化影响了弹舱流场压力分布,随L/D增大,舱内压力梯度逐渐升高,弹舱流场类型逐渐向闭式流动转变,舱内压力梯度主要影响武器纵向气动力特性,使武器在出舱段产生抬头力矩,L/D=9时,武器模型最大俯仰力矩出现在其离开弹舱约两倍弹径位置处,整体来讲,在所研究的分离区域内,弹舱流场对武器模型始终有一定影响;随L/D增大,侧向力系数(Cc)曲线波动有所降低,造成这种现象的原因是,武器侧向力主要源自弹舱前后端与自由来流垂直方向(Z轴方向)的横流作用,且弹舱前后端横流作用产生Cc方向相反,L/D较小时,弹舱前缘附近气流分离不明显,Cc主要由弹舱后端横流作用而产生,随L/D增大,弹舱前缘气流分离加剧,这样部分平衡了弹舱后端的横流作用,故Cc曲线波动降低;而对于偏航力矩系数(Cn)曲线,弹舱前后端横流作用产生的效果一致,因此,随L/D增大,Cn曲线波动增加。
|
| 图 9 武器分离时气动力特性曲线(Ma=0.6) Fig. 9 Weapon separation characteristics graphs |
跨声速时的试验结果与亚声速时相似,文中不再给出。
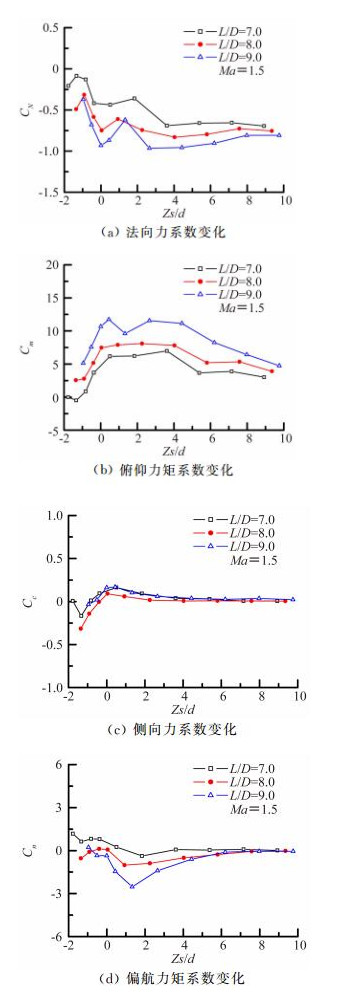
图 10为超声速(Ma=1.5)时的试验结果。图中表明,与亚、跨声速相比,超声速时,L/D变化对武器模型纵向气动力特性影响减弱,这主要是因为该马赫数下,对应L/D=7、8、9时弹舱流场类型均为开式流动,舱内压力梯度差异较小,值得注意的是,在Zs/d≈0~3.0范围内,CN曲线出现了向上的跳动点,而Cm曲线出现了向下的跳动点(L/D=9时表现的最明显),造成这种现象的原因可能是,武器模型离开弹舱到达某一位置时,其头部产生的激波在弹舱下方剪切层上发生反射,形成膨胀波并作用于武器模型后端,从而使该处压力降低,故产生正法向力和低头力矩;由于该马赫数下,上述三种长深比弹舱流场均具有开式流动特征,因此,弹舱前端气流的三维效应不明显,武器模型横、航向气动特性差异主要源自弹舱后端横流作用效果不同,随L/D增大,弹舱后端横流作用明显,Cn曲线在出舱段波动较大。
|
| 图 10 武器分离特性曲线(Ma=1.5) Fig. 10 Weapon separation characteristics graphs |
2.4 流动控制效果
鉴于篇幅,本节仅给出射流流量为27.3kg/h、Ma=1.5时的试验结果。
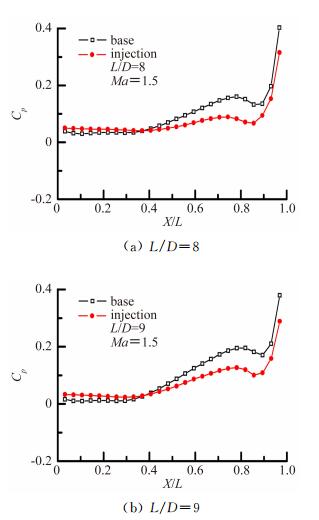
图 11给出了前缘射流对舱内静态压力分布影响。
|
| 图 11 舱底静压分布曲线 Fig. 11 Static pressure distributions of cavity floor |
图 11表明,采用流动控制后,弹舱前壁附近压力略有增大,舱内压力上升点相对位置后移,弹舱中后段压力明显降低,舱底压力分布更具开式流动特征。
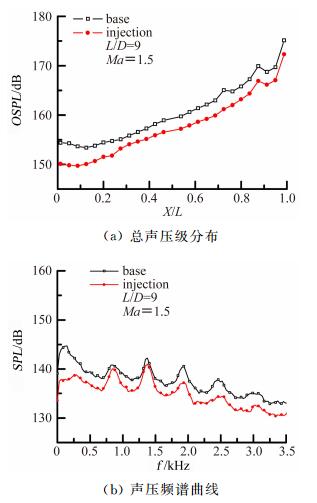
图 12给出了L/D=9时,前缘射流对弹舱流场气动声学特性影响。
|
| 图 12 射流对气动声学特性影响 Fig. 12 Curves of aero-acoustic characteristics |
图 12表明:采用该措施进行流动控制后,舱内所有测点的总声压级强度均有所降低,最大降低约4dB;分析频域范围内,典型测点声压能量均有所降低,声压频谱曲线上的峰值单调声均得到不同程度的抑制,第三峰值单调声降低超过3dB,弹舱流场气动声学环境得到较明显的改善。造成上述现象的原因有两方面,一方面射流改变了弹舱前缘来流方向,气流在到达弹舱之前将先压缩后扩张,上述作用将首先引发大范围的对流混合,进而产生小尺度涡导致小范围的对流混合,并最终因分子扩散而导致分子层次的混合,通过上述混合作用,流动中的不稳定因子被消除,流动的感受性大大降低,因此,当反馈信号激励弹舱前缘流动时,该处流动基本不会产生反映,故弹舱流场自持振荡机制完全被破坏,另外,该流动控制方法还将使弹舱前缘边界层厚度增大,来流抬升,气流在弹舱后缘撞击强度也有一定程度减弱,因此,反馈信号强度有所降低,这对弹舱流场气动噪声回路亦有一定破坏作用。
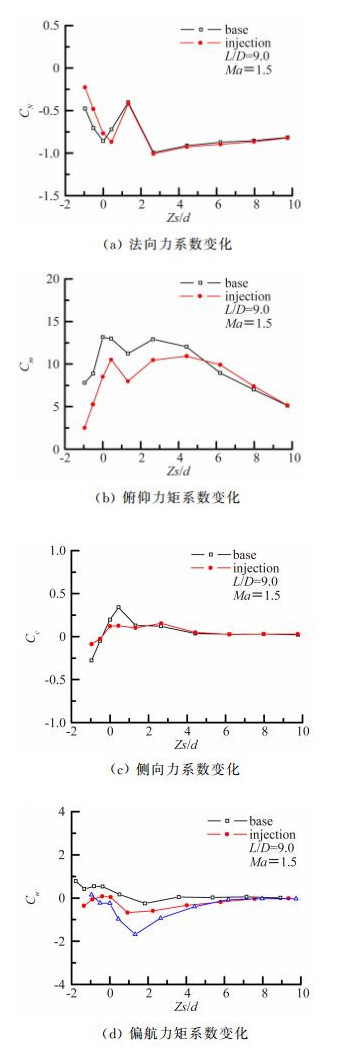
图 13给出了L/D=9时,前缘射流对内埋武器分离特性影响。
|
| 图 13 前缘射流对武器分离时气动力特性影响 Fig. 13 Weapon separation characteristics graphs |
图 13表明,采用前缘射流进行流动控制后,CN、 Cm曲线变化均更平缓,初离弹舱的附近区域内,武器模型产生的抬头力矩显著降低,Cc、Cn曲线波动也一定程度降低。造成上述现象的原因可能是,前缘射流将产生垂直来流方向的速度,两者合成后形成一股斜向外的气流,为改变气流方向,在弹舱前缘将产生一道斜激波,武器模型离开弹舱的一段区域内,该激波打在弹头上表面,产生低头力矩,另外,该斜激波还削弱了武器模型头部激波与弹舱流场剪切层的相互干扰,从而降低了出舱段武器模型法向力及俯仰力矩的波动;另外,该流动控制措施使弹舱前缘边界层厚度增加,这有利于减弱弹舱后端三维效应,从而使武器模型横航向气动特性得到改善。
3 结论1)舱内静压分布变化明显,随L/D减小,舱内压力梯度降低,弹舱流场类型向开式流动转变;
2)开式弹舱流场气动声学环境恶劣,最大总声压级强度可达170dB以上,且频谱曲线上存在多个明显的能量尖峰;
3)武器从舱内分离过程中可能产生较大的抬头力矩,影响机/弹安全分离;
4)在弹舱前缘施加射流能降低舱内静压梯度、抑制气动噪声,且有利于改善武器分离特性。
| [1] | Charwat A F, Roos J N, Dewey F C, et al. An investigation of separated flow-Part I: The pressure field[J].Aero. Sciences, 1960, 28:457–470. |
| [2] | Stallings R L, Wilcox F J. Experimental cavity pressure distributions at supersonic speeds[R]. NASA TP-2683, 1987. |
| [3] | Krishnamuty K. Acoustic radiation from two-dimensional rectangular cutouts in aerodynamic surface[R]. NACA TN-3487, 1955. |
| [4] | Long D F. An examination of pressure fluctuations in open cavities at transonic speeds[R]. AIAA 2003-3100. |
| [5] | Brooks D L, Hinckley E C. F-111A predicted weapon separation characteristics[R]. Pt.I, Weapons Loading Priorities I thru Ⅳ, Weapon Bay Separation. General Dynamics, Fort Worth Div., Rept. FZM-12-4520, Oct. 1966. |
| [6] | Stallings R L. Store separation from cavities at supersonic speeds[R]. AIAA 1982-0372. http://cn.bing.com/academic/profile?id=2160977572&encoded=0&v=paper_preview&mkt=zh-cn |
| [7] | Wilcox F J. Passive venting system for modifying cavity flow-fields at supersonic speeds[J].AIAA Journal, 1988, 26(3):374–376.DOI:10.2514/3.9902 |
| [8] | Sarpotdar S, Panickar P, Raman G. Cavity tone suppression using a rod in cross flow-investigation of shear layer stability mechanism[R]. AIAA 2009-700.. http://cn.bing.com/academic/profile?id=2153260104&encoded=0&v=paper_preview&mkt=zh-cn |
| [9] | Grove J, Shaw L. USAF/RAAF F-111 flight test with active separation control[R]. AIAA 2003-9. |
| [10] |
Wu Jifei, Luo Xinfu, Fan Zhaolin. Experimental investigation of cavity flow characteristics at subconic, transonic and super-sonic speeds[J].Journal of Experiments in Fluid Mechanics, 2008, 22(1):71–75. (in Chinese) 吴继飞, 罗新福, 范召林. 亚、跨、超声速下空腔流场特性实验研究[J]. 实验流体力学, 2008, 22(1) : 71–75. |
| [11] |
Luo baihua, Hu Zhangwei, Dai Changhui. Experimentalstudy on suppression of cavity oscillation by means of acoustic excitation[J].Journal of Nanjing University of Aeronautics & Astronautics, 1999, 31(1):1–5. (in Chinese) 罗柏华, 胡章伟, 戴昌晖. 声激励抑制空腔流激振荡的实验研究[J]. 南京航空航天大学学报, 1999, 31(1) : 1–5. |
| [12] |
Yang Dangguo, Wu Jifei, Luo Xinfu. Investigation on suppression effect of zero-net-mass-flux jet on aerodynamic noise inside open cavties[J].Acta Aeronautica Sinica, 2011, 32(6):1007–1014. (in Chinese) 杨党国, 吴继飞, 罗新福. 零质量射流对开式空腔气动噪声抑制效果分析[J]. 航空学报, 2011, 32(6) : 1007–1014. |
| [13] |
Muning A г. Aeroacoustic[M]. Cao Chuanyun translated. Beijing: Beihang University Press, 1993. (in Chinese) A.г.穆宁著, 曹传钧译.航空声学[M].北京航空航天大学出版社, 1993. |
| [14] | Rossiter J E. Wind-tunnel experimental on the flow over rectangular cavities at subsonic and rransonic speeds[R]. R. & M. No. 3438, 1964. |
| [15] |
Wu Jifei. Investigation on aerodynamiccharacteristics of internal weapons bay system[D]. PHD thesis. Mianyang: China aerodynamic research and development centre, 2013. (in Chinese) 吴继飞.内埋弹舱系统气动特性研究[D].博士学位论文.绵阳:中国空气动力研究与发展中心, 2013. |

