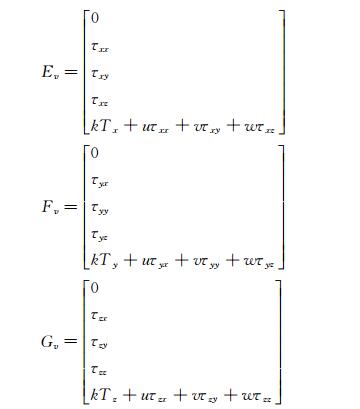风轮叶片的气动设计是风力机设计的重要环节,风轮叶片的气动外形直接影响到风力机的结构安全和气动性能。与常规飞行器的翼型相比,风轮叶片的翼型更为复杂,在叶片外形上,风轮叶片翼型后缘相对于常规飞行器的翼型更钝、相对厚度更大,且风轮叶片多工作在大迎角和低雷诺数状态下,因此风轮叶片的翼型既要有高升阻比,又要平稳的静态失速特性[1-2]。另外,围绕风轮叶片的流动是十分复杂的三维非定常过程,需要对风力机三维非定常流动进行深入研究。
随着计算机技术的不断发展,关于水平轴风力机的计算方法逐步由动量理论、叶素理论和涡流理论发展到动量-叶素方法和Euler/N-S数值模拟方法。黎作武[3]等采用正、反问题设计方法,设计完成了大型风力机组叶片的专用翼型族。刘雄[4]等研究了不同风力机叶片翼型后缘厚度对气动性能的影响情况,得到了翼型厚度对气动性能的影响规律;Srensen[5]等采用三维EllipSys3D程序对NREL Phase VI风力机风洞模型进行了带洞壁干扰的模拟研究,并采用动、静两个计算域以及周期性边界方法对风力机进行计算。许建华[6]等采用嵌套动网格对NREL Phase VI风力机进行了模拟研究,得到了叶片尾涡结构等流场细节;刘磊[7]等详细研究了湍流模型对风力机的典型截面压力分布和气动力系数的影响,部分湍流模型计算结果与实验值吻合较好。
在风力机叶片的数值模拟方法上,三维非定常数值计算逐渐成为风力机气动问题研究的重点。本文基于自主研发的大型“亚跨超CFD软件平台”(TRIP3.0)[8],开发了针对旋转类机械的非定常求解模块,对NREL Phase VI风力机模型[5, 9]进行了非定常数值模拟影响因素研究,影响因素主要包括时间步长、湍流模型、刚性动网格技术和动态拼接网格技术的影响三个方面。
1 计算方法 1.1 控制方程假设OXYZ是惯性笛卡儿坐标系,忽略彻体力,则Navier-Stokes方程可表达为:
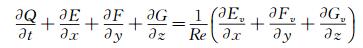 (1)
(1) 式中:
其中,ρ、u、v、w、p、e和h分别代表密度、x、y、z方向的绝对速度分量、压力、总能和总焓。
1.2 时间离散非定常时间离散采用双时间步方法,其中直角坐标系下的N-S方程可表达为:
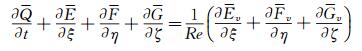 (2)
(2) 采用二阶后向差分,将上式在时间方向上展开:
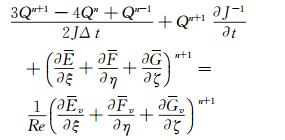 (3)
(3) 这是一个关于Qn+1的非线性方程,可通过引入一个伪时间步Δτ来求解Qn+1。
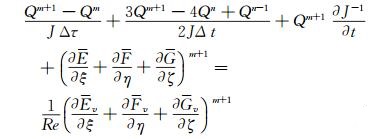 (4)
(4) 无粘通量的离散采用二阶精度的MUSCL-ROE格式,粘性通量的离散采用二阶中心格式。当m→∞,Qm+1=Qn+1,在伪时间步上变成一个定常问题,而且在伪时间上没有时间精度要求,可以采用定常求解方法迭代计算,多重网格技术、并行计算技术等各种加速收敛的措施也可以继续使用。只要伪时间上的定常问题收敛,真实时间上的求解精度仍然是二阶的。
2 研究模型计算对象为NREL Phase VI风力机模型,该风力机模型由美国国家可再生能源实验室(NREL)设计,采用双叶片方案,叶片半径为5.03m,主要采用S809翼型进行缩放和扭转得到,叶根由圆柱段和过渡段组成,在建模过程中,加入了简化后的机舱。来流风速v=10m/s,转速为72r/min。
本文分别生成了动态拼接网格和刚性运动网格,动态拼接网格是部分区域(旋转域)网格旋转,其他区域(静止域)网格静止,而刚性运动网格则是整个计算域网格均旋转。
2.1 动态拼接网格拼接网格又称面搭接网格,其特点是在网格块与块之间通过公共面进行连接,网格线不需要对接,网格块之间的拓扑关系被交界面切开,因此,网格块之间的拓扑关系相互独立,并通过交界面进行信息传递。其优点是复杂外形网格生成相对简单,网格量较小;计算中采用通量守恒的交界面传值,保证计算精度。动态拼接网格方法是在每一个真实时间步长中,将旋转域网格旋转一个固定角度,并重新定义网格拼接关系;通过旋转域的网格旋转,实现风力机标模的非定常数值模拟。
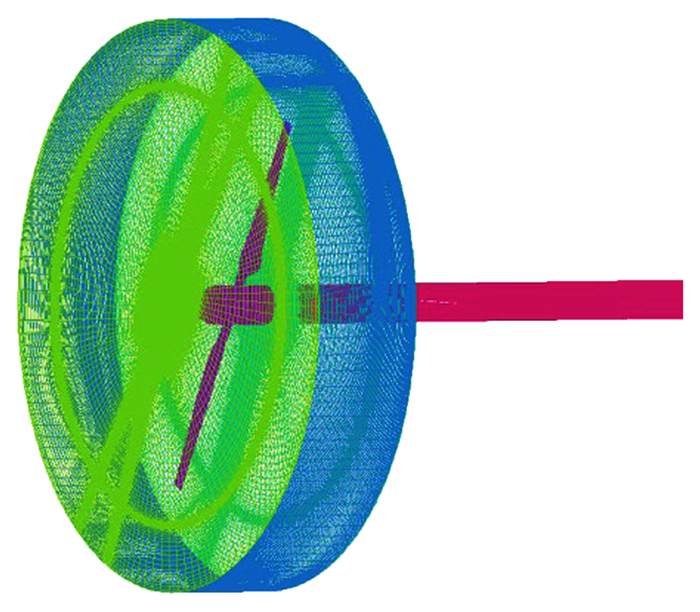
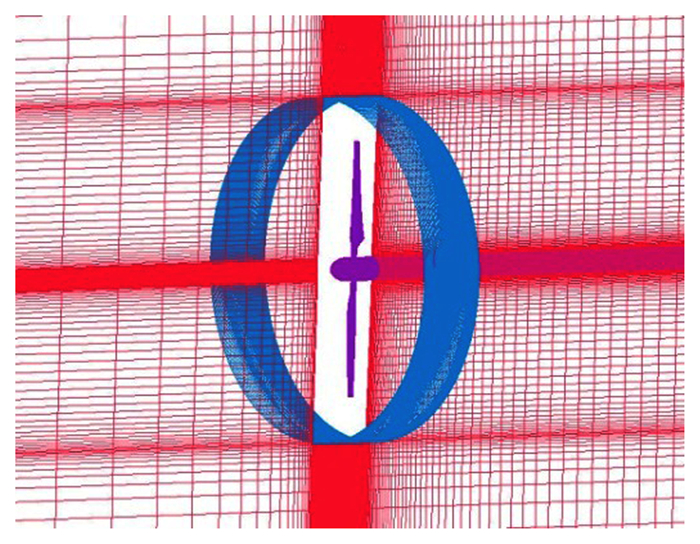
本文动态拼接网格的网格规模为680万,其中旋转部分半径为叶片长度的1.3倍,网格量为460万。图 1和图 2给出了旋转域网格以及拼接处网格示意图。根据流动的特点,远场选取采用上下游均延伸30倍叶高,径向延伸15倍叶高的圆柱计算域。
|
| 图 1 旋转域网格示意图 Fig. 1 Mesh slice of the rotational subzone |
|
| 图 2 拼接处网格示意图 Fig. 2 Mesh slice of the cross subzone |
2.2 刚性运动网格
刚性运动网格技术,即整个网格随物体一起作刚体运动,如单独风轮网格,由于风轮叶片的旋转运动为轴对称,故可以采用整个网格的定轴旋转来模拟风轮叶片的非定常运动。刚性动网格技术的优点是:在整个非定常计算过程中,计算网格无需重新生成,直接通过运动关系给出,因此该方法计算量较小,且网格质量能保证,计算结果更为精细。不足之处是:该方法仅适用于单个刚性物体的非定常运动,对于组合体或者多体分离甚至变形体等复杂问题而言,这类方法不能适用。其次,远场网格距离网格中心较远,网格的位移和速度变化较大,在边界处理上有诸多不便[10]。
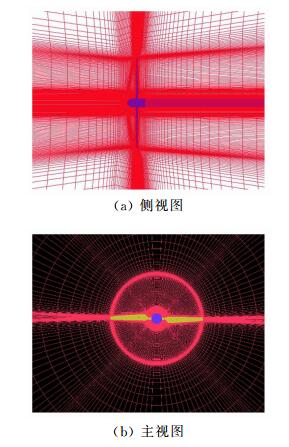
本文刚性运动网格采用点点对接方式生成,网格规模为1028万,网格块数为172块,远场选取与拼接网格大小相同。图 3给出了局部网格的侧视图和主视图。本文通过在求解器中自动更新每个真实时间步下网格节点坐标和速度等参数值,实现对风力机标模的非定常数值模拟。
|
| 图 3 刚性运动网格主视图 Fig. 3 Mesh slice of the dynamic patched grid |
3 计算结果分析
本节首先基于刚性运动网格的非定常方法,分析了不同真实时间步长、不同湍流模型对计算结果的影响,其次结合动态拼接网格进行了不同动网格技术的非定常计算结果对比。基于刚性运动网格和动态拼接网格的数值模拟分别采用48核和24核并行,每个计算状态风轮旋转两圈,每个真实时间步网格旋转3°时的计算周期约为96小时。
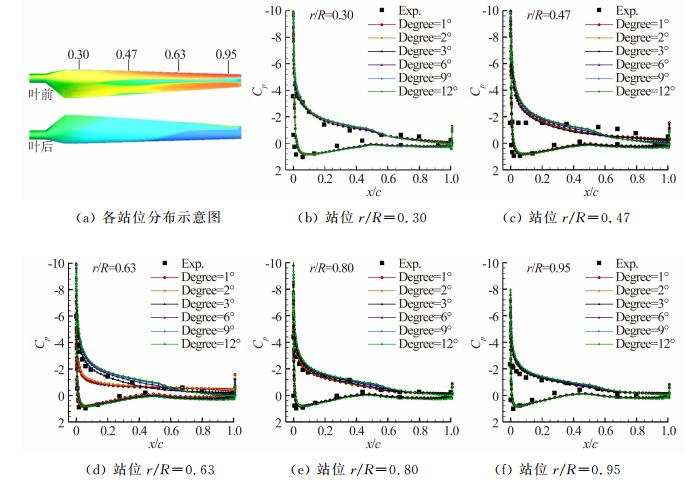
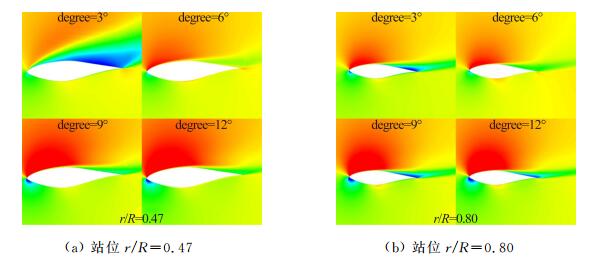
3.1 时间步长对数值模拟结果的影响计算采用SA湍流模型,对风力机进行了刚性运动网格下的非定常模拟,来流风速v=10m/s。图 4给出了每个真实时间步网格分别旋转Degree=1°、2°、3°、6°、9°、12°时,叶片各站位的压力分布情况。可以看出:采用不同的时间步长,对靠近叶根和叶梢站位上的压力分布影响不明显,而对叶片中间站位(r/R=0.63)影响显著,当Degree=3°时,计算结果更接近实验值。从图 5中周向速度云图可以看出,在r/R=0.47站位上,每个真实时间步网格旋转3°的叶偏后出现明显分离,且分离泡较其他情况更大。在r/R=0.80站位上,四种真实时间步长计算结果相近,四种真实时间步长下分离泡大小基本一致。
|
| 图 4 不同真实时间步长各站位压力分布 Fig. 4 Pressure distribution on different suctions with different real time steps |
|
| 图 5 站位r/R=0.47和0.80处周向速度云图(来流风速v=10m/s) Fig. 5 Circumferential speed distribution on r/R=0.47 and 0.80 |
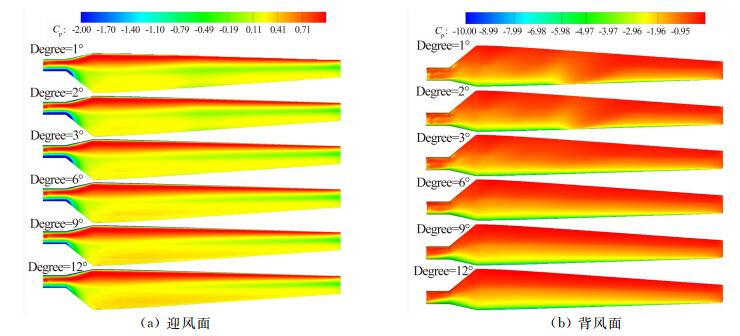
图 6给出不同真实时间步长叶片迎风/背风面压力分布云图,发现Degree=6°~12°压力云图相似,Degree=1°~2°压力云图相似,其中Degree=3°处于临界状态,且在叶片中间站位压力分布与实验值更接近。
|
| 图 6 不同时间步长叶片迎风/背风面压力云图(来流风速v=10m/s) Fig. 6 Pressure distribution on up/down suctions with different real time steps |
3.2 湍流模型对数值模拟结果的影响
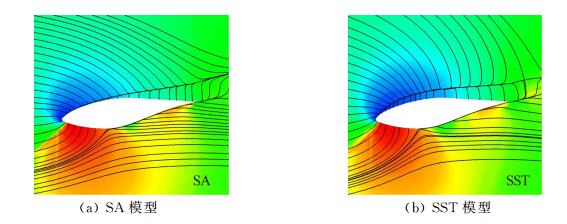
为了比较不同湍流模型对数值模拟结果的影响,本节分别采用SA和SST湍流模型,基于刚性运动网格方法对风力机标模进行了非定常模拟,并比较了叶片上流动参数。图 7给出了来流风速v=10m/s时各站位压力分布情况。通过与实验结果对比发现,采用SA湍流模型得出的结果与实验值吻合较好;两种湍流模型对压力面Cp分布的基本没有影响,但对吸力面Cp分布影响较大,SA较SST模型更接近实验值。图 8给出了站位r/R=0.30处压力云图和空间流线图,可以看出,两种模型计算的结果都出现分离,SST得到的分离泡较SA大。

|
| 图 7 不同湍流模型各站位压力分布 Fig. 7 Pressure distribution on different suctions with different turbulence models |
|
| 图 8 站位r/R=0.30处压力云图和空间流线图 Fig. 8 Pressure distribution and streamlines on r/R=0.30 |
计算结果显示,采用SA湍流模型得到的计算值与实验值吻合良好,且略优于SST模型,故以下计算采用SA湍流模型。
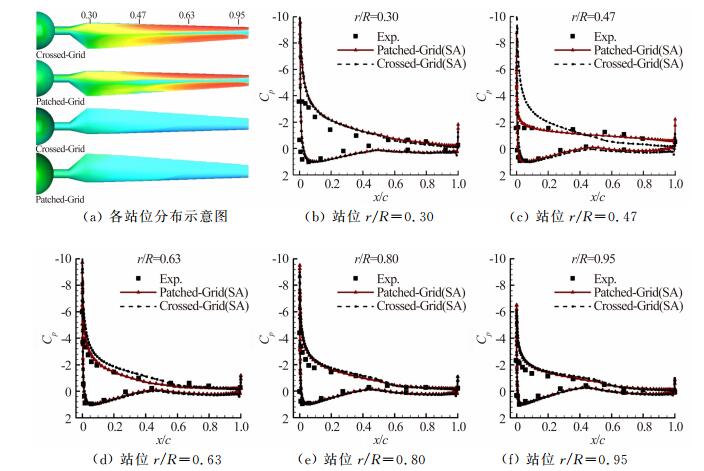
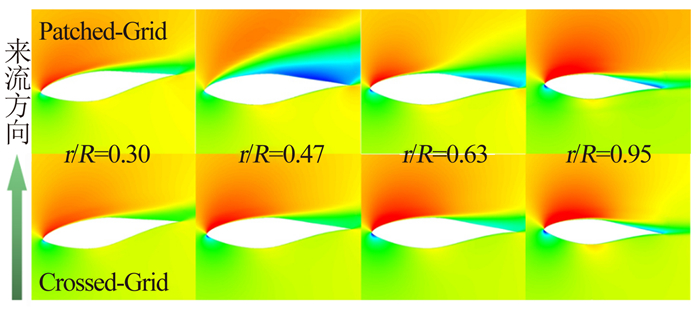
3.3 不同动网格技术对数值模拟结果的影响在上述研究工作的基础上,本节分别采用刚性运动网格(Patched-Grid)和动态拼接网格(Crossed-Grid)对风力机进行了非定常对比计算。图 9给出了不同网格技术下,来流风速v=10m/s时,采用SA湍流模型得到的叶前、后压力云图和各站位压力分布情况。从图 9可以看出,动态拼接网格计算的压力分布趋势与刚性运动网格的基本相同。从压力分布的结果可以得出,采用刚性运动网格的计算结果与实验值更接近。图 10为采用SA湍流模型和两种网格方式得到的叶片各典型站位的周向速度云图,可以看出,采用动态拼接网格得到的分离泡较刚性运动网格的小,特别是在r/R=0.47站位处,刚性运动网格计算的分离区很明显,压力分布与实验结果相吻合,而动态拼接网格计算的分离点后移。
|
| 图 9 不同动网格技术各站位压力分布 Fig. 9 Pressure distribution on different suctions with dynamic patched-grid/crossed-grid |
|
| 图 10 不同站位下周向速度云图 Fig. 10 Circumferential speed distribution on different suctions |
4 结论
本文基于自主研发的软件平台TRIP3.0,建立了旋转类机械的非定常求解模块。采用NREL Phase VI风力机模型,开展了时间步长、湍流模型、刚性动网格技术和动态拼接网格技术等因素对该数值模拟结果的影响研究。主要结论如下:不同的时间步长、湍流模型和网格生成策略主要影响风力机叶片吸力面的流动结构,进而影响到吸力面的压力分布,而对压力面的流动结构和压力分布基本没有影响;采用刚性运动网格结合SA湍流模型所得到的压力分布更接近实验值。
致谢: 本文是在TRIP软件开发小组的共同努力下完成的,在此对课题组成员洪俊武研究员、王光学副研究员、李伟研究实习员、孙岩助理研究员、李松工程师表示衷心的感谢!| [1] |
He D X. The status and vista of wind engineering studies in China[J].Mechanics and Engineering, 2002, 24(4):10–19. (in Chinese) 贺德馨. 我国风工程研究现状与展望[J]. 力学与实践, 2002, 24(4) : 10–19. |
| [2] |
He D X.
Wind engineering and industrial aerodynamics[M]. Beijing: National Defence Industry Press, 2006 : 81 -96.
(in Chinese) 贺德馨. 风工程与工业空气动力学[M]. 北京: 国防工业出版社, 2006 : 81 -96. |
| [3] |
Li Z W, Chen J, Chen B, et al. Design of advanced airfoil families for wind turbines[J].Acta Aerodynamica Sinica, 2012, 30(1):130–136. (in Chinese) 黎作武, 陈江, 陈宝, 等. 风力机组叶片的先进翼型族设计[J]. 空气动力学学报, 2012, 30(1) : 130–136. |
| [4] | Sørensen N N, Michelsen J A, Schreck S. Navier-Stokes predictions of the NREL Phase VI rotor in the NASA Ames 80-by-120 wind tunne[R]. AIAA-2002-14498. |
| [5] |
Xu J H, Song W P, Han Z H. Simulation of flow fields around wind turbine blade based on chimera-grid methodology[J].Acta Engergiae Solaris Sinica, 2010, 31(1):91–95. (in Chinese) 许建华, 宋文萍, 韩忠华. 基于嵌套网格技术的风力机叶片绕流数值模拟[J]. 太阳能学报, 2010, 31(1) : 91–95. |
| [6] |
Liu L, Xu J Z. The effects of turbulence model on the aerodynamic performance prediction of wind turbine blade[J].Journal of Engineering Thermophysics, 2009, 30(7):1136–1139. (in Chinese) 刘磊, 徐建中. 湍流模型对风力机叶片气动性能预估的影响[J]. 工程热物理学报, 2009, 30(7) : 1136–1139. |
| [7] |
Liu X, Chen Y, Ye Z Q. Research on the aerodynamic performance prediction model forhor-izontal axis wind turbine[J].Acta Engergiae Solaris Sinica, 2005, 26(6):792–800. (in Chinese) 刘雄, 陈严, 叶枝全. 水平轴风力机气动性能计算模型[J]. 太阳能学报, 2005, 26(6) : 792–800. |
| [8] |
Wang Y T, Wang G X, Zhang Y L. Drag prediction of DLR-F6 configuration with TRIP2.0 software[J].Acta Aerodynamica Sinica, 2009, 27(1):108–113. (in Chinese) 王运涛, 王光学, 张玉伦. 采用TRIP2.0软件计算DLR-F6构型的阻力[J]. 空气动力学学报, 2009, 27(1) : 108–113. |
| [9] | Hand M M, Simms D A, Fingersh L J, et al. Unsteady aerodynamics experiment phase VI: wind tunnel test configurations and available data campaigns[R]. NREL/TP-500529955, NREL, Golden, CO, 2001. |
| [10] |
Zhang L P, Deng X G, Zhang H X. Reviews of moving grid generation techniques and numerical methods for unsteady flow[J].Advances in Mechanics, 2010, 40(4):424–447. (in Chinese) 张来平, 邓小刚, 张涵信. 动网格生成技术及非定常计算方法进展综述[J]. 力学进展, 2010, 40(4) : 424–447. |