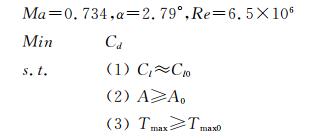2. 北京宇航系统工程研究所, 北京 100076
2. Beijing Institute of Aeronautical Systems Engineering, Beijing 100076, China
数值优化方法能够为设计人员提供满足约束要求的计算结果和相应的设计参考,因而在气动设计中得到了广泛应用。然而一般在气动数值优化设计过程中需要进行大量的气动分析,耗时较长,大大降低了设计的效率,如果在气动优化设计中,合理地引入代理模型,在保证一定计算精度的条件下可以有效的减少计算周期[1]。而为了减少建立代理模型的时间进一步提高设计的效率,可以运用有效的插值和选样方法,同时这样也可以在样本点相同时,有效地提高代理模型预测精度[2]。因此,本文建立了采用自适应选样的Kriging自适应代理模型和支持向量回归(Support Vector Regression, SVR)自适应代理模型,并与优化算法相结合进行气动优化设计。对这两种自适应代理模型进行了函数测试,并且对比分析了这两种自适应代理模型的特点,然后应用到翼型减阻优化问题中。
1 自适应代理模型代理模型是指通过数学手段构造的计算量小、但计算结果与数值分析或物理试验结果相近的近似数学模型,以替代原分析模型或物理试验用于优化设计[3]。代理模型也被称为“模型的模型”,具有结构简单,计算量小的优点,适用于气动优化设计中构建气动分析模型。
1.1 Kriging自适应代理模型Kriging方法[4]对非线性模型有很好的逼近能力,不仅可以很好地解决各向同性问题,而且还可以良好地解决各向异性问题。因此本文首先采用Kriging方法来构建代理模型。在构建代理模型时,样本决定着代理模型在整个设计空间的精度[5]。由于大多数代理模型在预测点附近存在不确定性,当样本点较少,模型精度较低时,会出现局部收敛问题。同时,在整个设计空间内,样本选取方法一般为有序的离散分布,却无法依据实际问题在极值点处集中分布,以反映问题特性[6]。比如采用拉丁超立方方法[7]和Kriging方法构建的Kriging代理模型,其稳健性较好,能利用其预测能力来对所求问题的解空间进行预估,可以在一定程度上减少计算时间[8]。然而,该Kriging代理模型依然存在当样本点稀疏、模型精度低时,可能无法找到全局最优解的问题。
如果能通过一种系统的方法来保证目标函数预测值的不确定性最小,就可以保证或者提高代理模型的预测精度。为了最小化不确定部分,需要加强样本点在非线性区域的分布。可以采用EI函数[9]来实现。EI函数是合理地加强样本非线性部分而发展的选样标准,它通过权衡现有样本的密度概率在当前预测值的极值处,得到最大值。其中,EI函数为:
 (1)
(1) 上式中ymin是当前样本点中的最小值Φ是标准正态分布函数,ϕ是标准分布概率密度函数,ŷ和s是x处的预测值和预测标准差。选择EI函数的最大值处添加样本点,可以平衡Kriging方法中不同样本点间的距离,并驱使空间样本点自适应分布,从而实现根据求解问题的特性来自适应选择样本点。
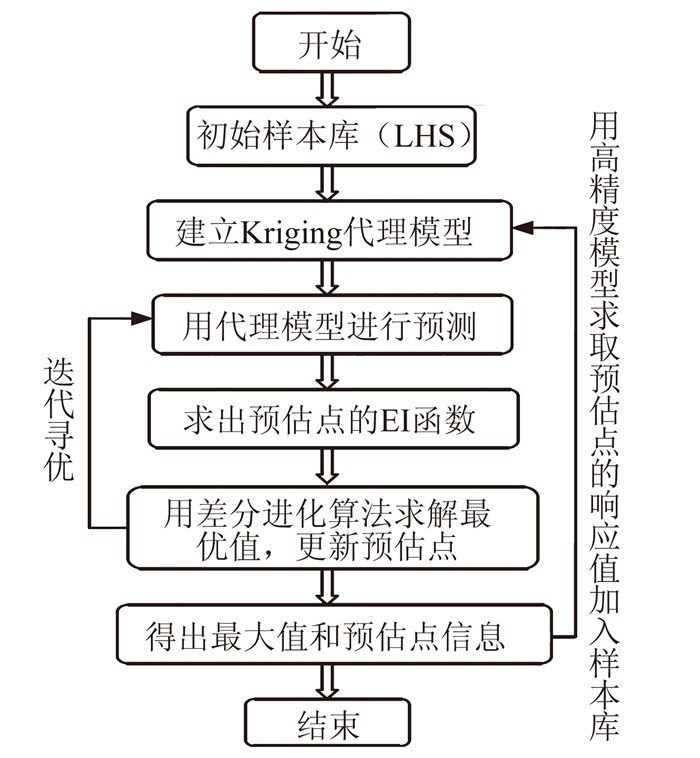
将自适应选样和Kriging方法结合起来,即可构建出Kriging自适应代理模型。Kriging自适应代理模型的流程如图 1所示:
|
| 图 1 Kriging自适应代理模型的流程 Fig. 1 Sketch of Kriging adaptive surrogate model |
1)在设计空间内,用拉丁超立方方法(LHS)建立初始样本库;
2)采用Kriging方法建立设计变量和目标变量的近似映射关系;
3)以EI函数为目标函数,用Kriging模型进行预测,求出初始预估点种群x的响应值y;
4)本文采用差分进化算法(DE)进行迭代寻优,找出使EI函数值最大的点作为添加的样本点;
5)将寻优得到的样本点采用高精度模型来计算目标变量值,添加到样本库中;
6)更新Kriging自适应代理模型,重复步骤2至步骤5,直到添加完所需要的自适应样本点。
1.2 支持向量回归(SVR)自适应代理模型在构建代理模型时,包括Kriging方法在内的大多数近似方法都基于经验最小化原则,样本影响着代理模型在整个设计空间的精度。为了提高优化设计效率,训练代理模型的样本数目需要尽可能的少。尤其是针对于耗时较长的气动优化问题。SVR能够通过有限的样本信息寻求模型的复杂性和学习能力间的最佳折中,在处理小样本、非线性和高维模型识别等问题上具有突出的优势[10]。因此本文在Kriging自适应代理模型基础上构建SVR自适应代理模型。
Kriging自适应选样的原理就是利用EI函数最小化Kriging代理模型不确定部分(不确定部分与误差密切相关),通过添加样本点加强样本点在非线性区域的分布。可以看出在自适应选样中,代理模型的不确定部分常用来指出将要添加选样点的位置,然而不是每一种代理模型都能够明确定义不确定部分,例如径向基神经网络和支持向量回归[11]。缺少这方面信息的代理模型在自适应选样方面会受到限制。如果我们借鉴可以明确定义不确定部分的代理模型,将其添加样本点位置的信息输入给没有这方面信息的代理模型,例如将Kriging中的不确定部分给支持向量回归,这样SVR方法也可以进行自适应选样。
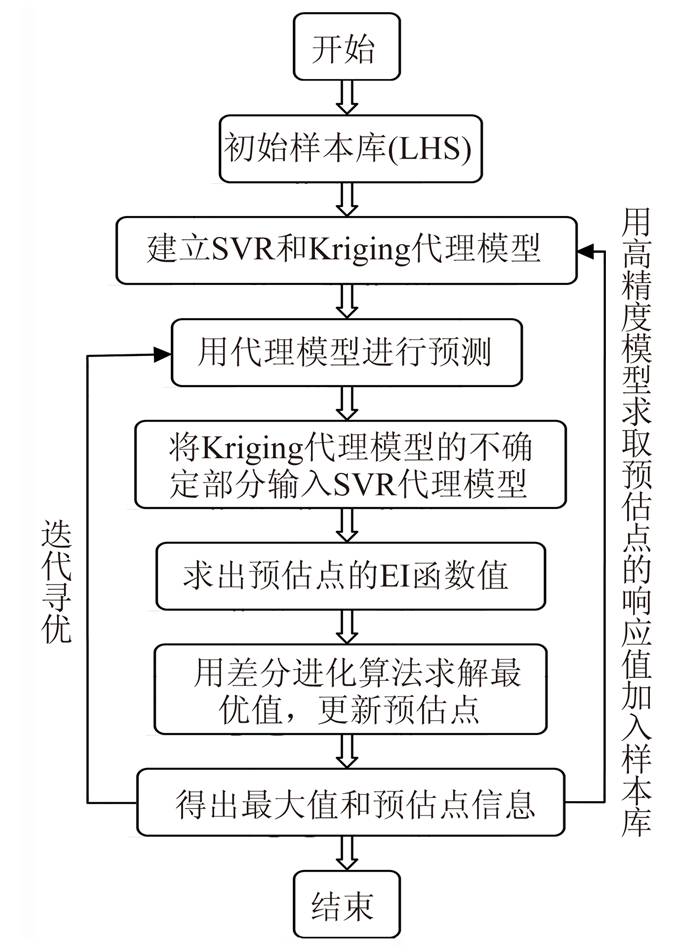
将SVR自适应选样和SVR方法结合起来,即可构建出SVR自适应代理模型,本文采用的SVR方法使用径向基核函数将输入向量映射到高维空间进行线形回归[12]。SVR自适应代理模型的流程如图 2所示:
|
| 图 2 SVR自适应代理模型的流程 Fig. 2 Sketch of SVR adaptive surrogate model |
1)在设计空间内,用拉丁超立方方法(LHS)抽样建立初始样本库;
2)采用SVR方法和Kriging方法同时建立设计变量和目标特性数据的近似映射关系;
3)将Kriging代理模型的不确定部分输入给SVR代理模型,以EI函数为目标函数,用已建成的SVR模型进行预测,求出初始预估点种群x的响应值y;
4)用DE优化算法进行迭代寻优,找出使EI函数值最大的点作为添加的样本点;
5)将寻优得到的样本点采用高精度模型来计算目标变量值,添加到样本库中;
6)更新SVR自适应代理模型,重复步骤2至步骤5,直到添加完所需要的自适应样本点。
2 函数测试分析为了分析自适应代理模型的性能,本文选用两种典型的测试函数——Sphere函数、Ackley函数来进行测试分析。本文所用到的典型测试函数为:
1) Sphere函数:
 (2)
(2) 搜索范围:-100≤xi≤100
全局最小值:min(f1)=f1(0, …, 0)=0
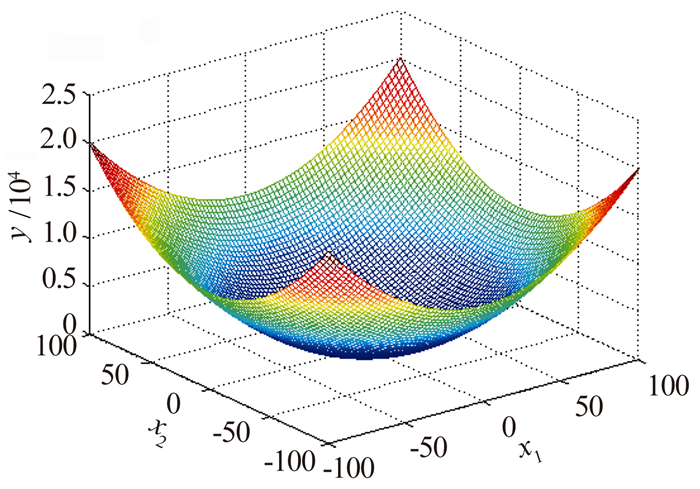
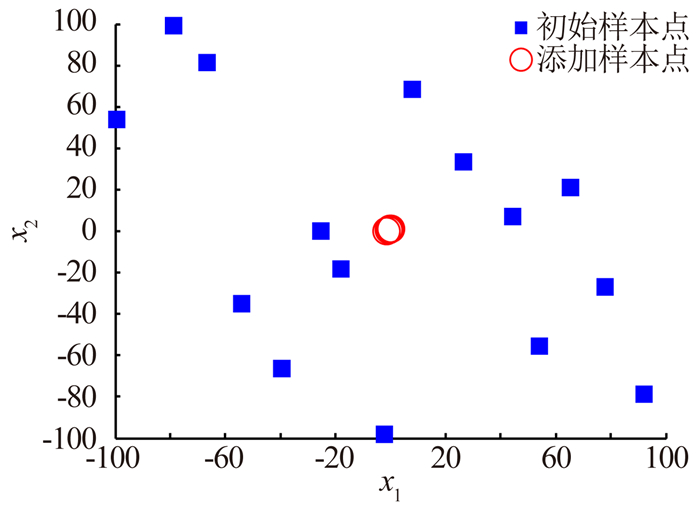
该函数又称DeJong函数,是一个非线性的对称单峰函数,其二维函数示意图见图 3。
|
| 图 3 二维Sphere函数示意图 Fig. 3 Schematic diagram of 2-D Sphere function |
2) Ackley函数:
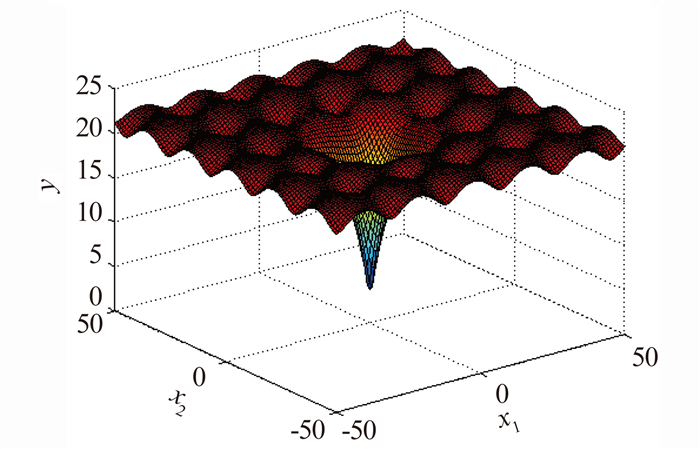
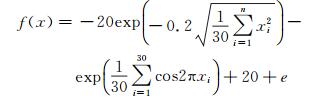 (3)
(3) 搜索范围:-50≤xi≤50
全局最小值为:min(f2)=f2(0, …, 0)=0
该函数是一个连续、旋转、不可分离的多峰函数,存在大量的局部最优点,其二维函数示意图见图 4。
|
| 图 4 二维Ackley函数示意图 Fig. 4 Schematic diagram of 2-D Ackley function |
Sphere二维函数中,初始样本点个数为15个,自适应代理模型选样添加样本点个数为5个。
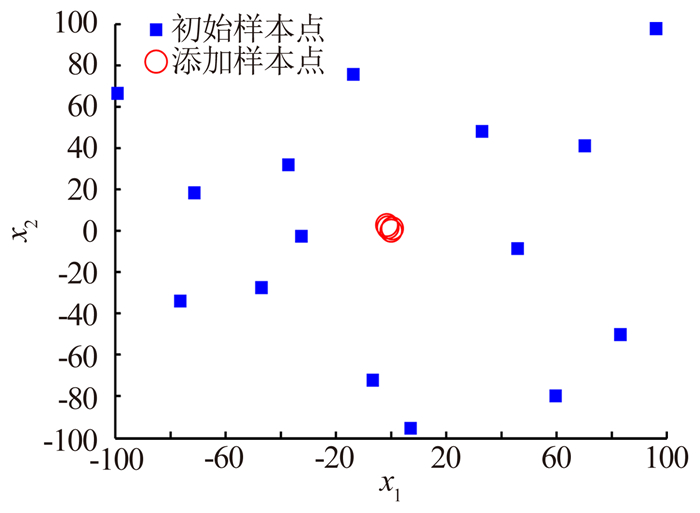
Ackley二维函数中,初始样本点个数为50个,自适应代理模型选样添加样本点个数为25个。
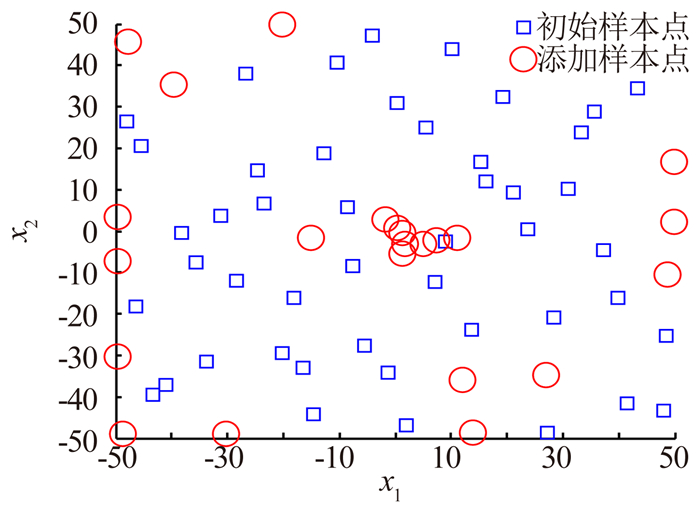
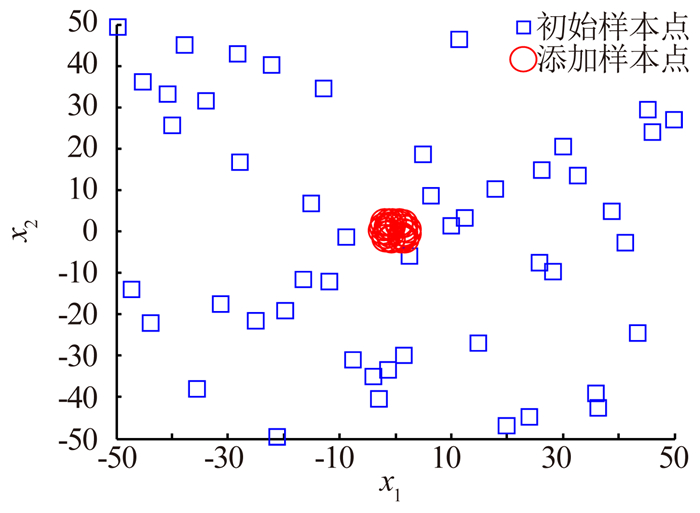
从图 5、图 6、图 7、图 8可以看出对于简单的单峰Sphere函数和复杂的多峰Ackley函数,Kriging自适应代理模型结果显示添加的样本点会明显集中在最小值和边界附近,而SVR自适应代理模型添加的样本点主要集中在最小值附近,并且比Kriging自适应代理模型添加的样本点更加集中,因此对函数极值的趋势描述更为准确。
|
| 图 5 Kriging自适应代理模型选样分布示意图 Fig. 5 Sampling distribution of Kriging adaptive surrogate model |
|
| 图 6 SVR自适应代理模型选样分布示意图 Fig. 6 Sampling distribution of SVR adaptive surrogate model |
|
| 图 7 Kriging自适应代理模型选样分布示意图 Fig. 7 Sampling distribution of Kriging adaptive surrogate model |
|
| 图 8 SVR自适应代理模型选样分布示意图 Fig. 8 Sampling distribution of SVR adaptive surrogate model |
一维Sphere函数中,一般代理模型样本点为20个;自适应代理模型初始样本点为15个,添加样本点为5个。一维Ackley函数中,一般代理模型样本点为75个;自适应代理模型初始样本点为50个,添加样本点为25个。表 1为测试函数结果比较。
| 测试 函数 |
取10次选样样本点最小值的平均值 | |||
| Kriging 代理模型 |
Kriging自适应 代理模型 |
SVR 代理模型 |
SVR自适应 代理模型 |
|
| 一维Sphere | 2.6486 | 7.9816×10-5 | 0.5405 | 0.0139 |
| 一维Ackley | 1.8566 | 0.0861 | 0.5612 | 0.0025 |
从表 1可以看出,自适应代理模型能够选出更靠近最小值处的样本点,从而在样本点数一致的情况下,自适应代理模型与真实值的误差较小,更能真实的反映设计空间。对于一维Sphere函数,两种自适应代理模型的初始样本点和添加样本点数目和比例一致时,Kriging自适应代理模型选样点最小值的均值比SVR自适应代理模型选样点最小值的均值更接近最小值。因此对于简单问题当样本点选取的足够多时,Kriging自适应代理模型预测精度高于SVR自适应代理模型选样精度。而对于一维Ackley函数,SVR自适应代理模型选样点最小值的均值比Kriging自适应代理模型选样点最小值的均值更接近最小值,因此对于非线性较高的问题,则是SVR自适应代理模型预测精度高于Kriging自适应代理模型预测精度。
3 翼型算例测试为了验证代理模型对气动性能的预测能力,本文选取翼型升力及阻力作为预测目标进行代理模型的测试。并对Kriging自适应代理模型和SVR自适应代理模型的预测能力及误差进行验证。选取150个初始样本点,添加50个样本点建立Kriging和SVR自适应代理模型;为了进行比较,另选取200个点建立Kriging和SVR代理模型。其中,翼型参数化方法为HicksHenne型函数方法[13],设计变量个数为14个,使用拉丁超立方设计生成初始样本数据。样本的气动分析方法,采用RANS方程数值解法,离散方法为中心格式的有限体积法,湍流模型采用SA模型。翼型计算状态为Ma=0.734,α=2.79°,Re=6.5×106。代理模型在非样本点的预测误差分别取平均绝对误差(Average Absolute Error, AAE),平均相对误差(Average Relative Error, ARE),均方差(Mean Relative Square Error, MRSE),以及最大绝对误差(Max Absolute Error, MAE),测试结果如下:
1) Kriging自适应代理模型翼型气动力预测结果
2) SVR自适应代理模型翼型气动力预测结果
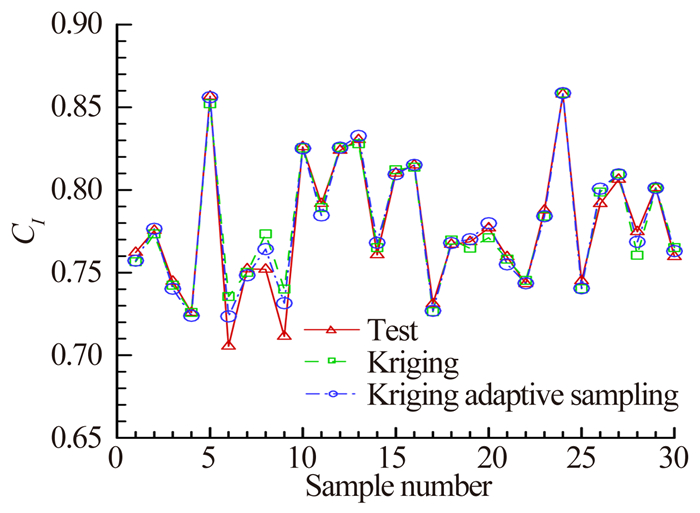
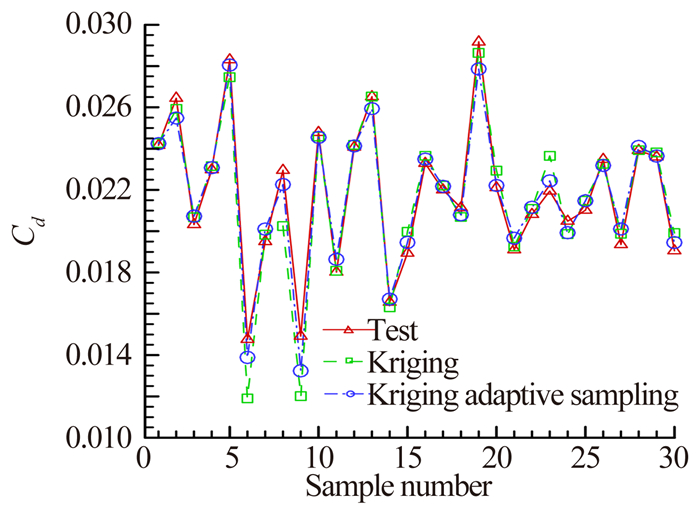
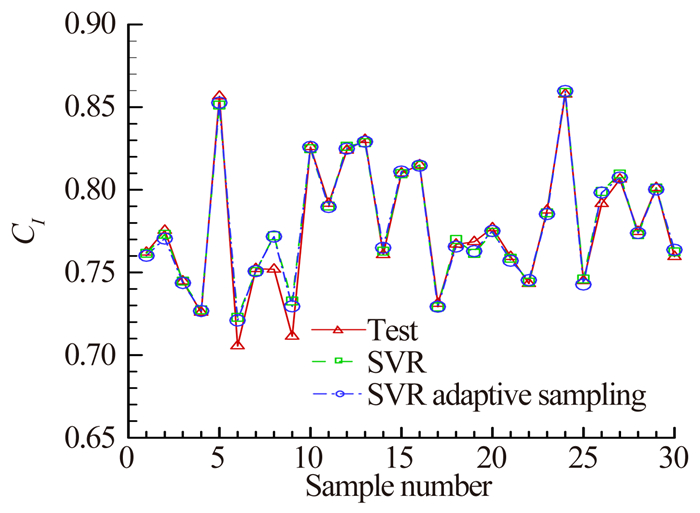
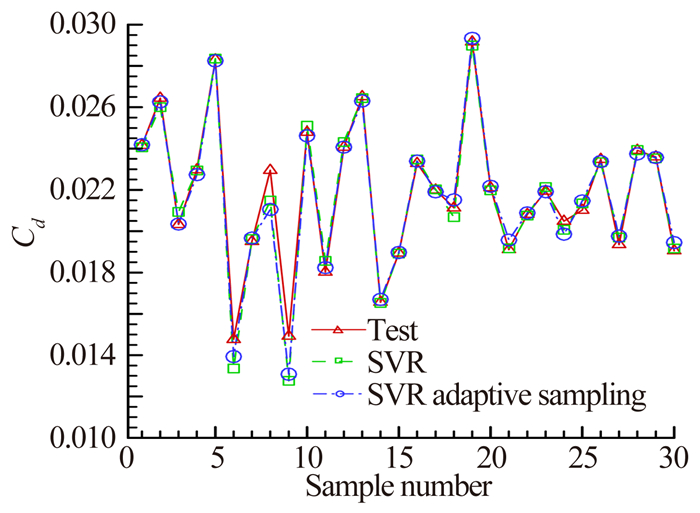
从表 2和表 3可以看出,由于平均绝对误差、平均相对误差以及最大绝对误差是反映代理模型的预测精度,所以从这三种误差中可以看出两种自适应代理模型比一般代理模型的预测误差小。均方差反映着样本点的离散程度,因为自适应代理模型的添加样本点都集中在目标问题的极值附近,因此离散程度小,均方差也较小。从图 9至图 12可以看出200个样本点时,两种自适应代理模型预测升力系数和阻力系数趋势与测试数据一致,预测精度较高。而一般代理模型预测升力系数和阻力系数趋势的准确度也比较准确。
| 误差 | Kriging代理模型 | Kriging自适应代理模型 | |
| Cl | AAE | 0.005429 | 0.005188 |
| ARE | 0.007248 | 0.006900 | |
| MRSE | 0.037349 | 0.035938 | |
| MAE | 0.028679 | 0.022302 | |
| Cd | AAE | 0.000648 | 0.000602 |
| ARE | 0.032025 | 0.030341 | |
| MRSE | 0.003849 | 0.003478 | |
| MAE | 0.003812 | 0.002683 |
| 误差 | SVR代理模型 | SVR自适应代理模型 | |
| Cl | AAE | 0.003899 | 0.003732 |
| ARE | 0.005185 | 0.004968 | |
| MRSE | 0.036745 | 0.036636 | |
| MAE | 0.021317 | 0.019805 | |
| Cd | AAE | 0.000344 | 0.000321 |
| ARE | 0.018293 | 0.016725 | |
| MRSE | 0.003646 | 0.003565 | |
| MAE | 0.002163 | 0.001895 |
|
| 图 9 翼型升力系数分析结果比较 Fig. 9 Results of lift coefficient |
|
| 图 10 翼型阻力系数分析结果比较 Fig. 10 Results of drag coefficient |
|
| 图 11 翼型升力系数分析结果比较 Fig. 11 Results of lift coefficient |
|
| 图 12 翼型阻力系数分析结果比较 Fig. 12 Results of drag coefficient |
通过SVR自适应代理模型、Kriging自适应代理模型的气动性能预测结果相比,SVR自适应代理模型的四种预测误差明显较小,这是主要是因为SVR方法比较适用于求解高维度小样本的问题,这里小样本不是指样本的绝对数量小,而是在问题的同等复杂程度时,SVR方法所需的样本数相对其他方法是比较少的。在气动力预测结果中相对建模误差较大的测试点主要是因为气动力系数绝对值较小,因此相对误差会较大。
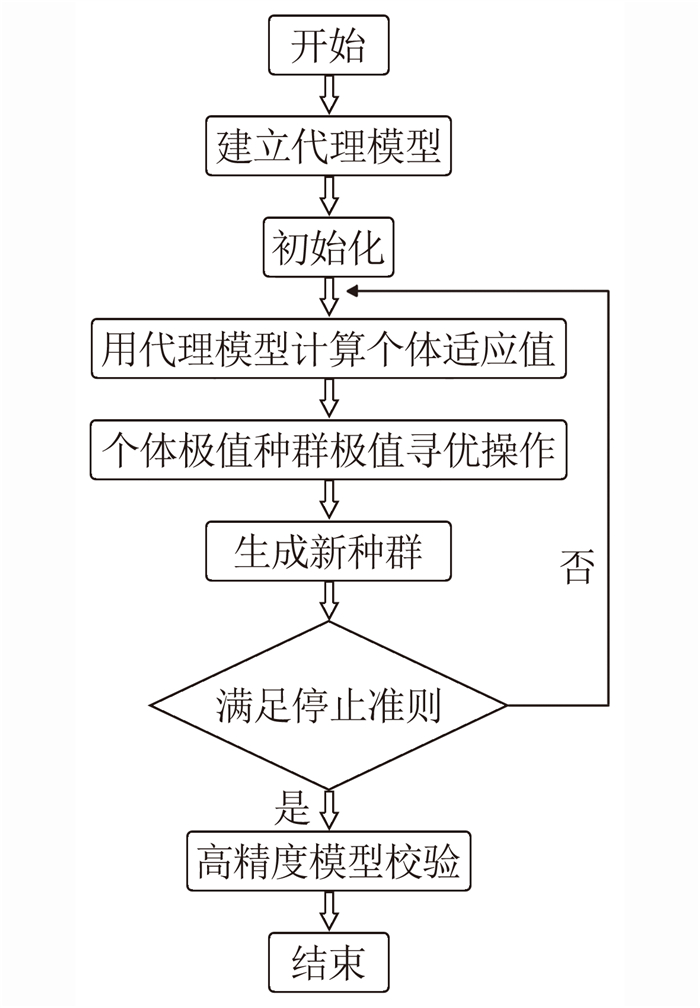
4 基于自适应代理模型的优化算法本文的代理模型和优化算法结合采用松耦合方式[14],分别将一般代理模型和自适应代理模型与粒子群优化算法相结合形成基于代理模型的优化方法。这种优化方法是将代理模型作为一种对真实目标函数的代理,在优化算法搜索过程中使用代理模型求解种群中每个个体的适应度值,最终得到优化目标解。两种代理模型和优化算法松耦合方式的流程如图 13所示。
|
| 图 13 优化流程图 Fig. 13 Sketch of surrogate model optimization |
5 气动优化算例
以RAE2822翼型为初始翼型,考虑其在11000m高空的巡航性能,对其进行减阻优化设计。设计状态为:
优化目标为最小化翼型阻力系数,约束条件为升力系数保持不变,翼型的面积和最大厚度不减小。翼型几何参数化采用Hicks-Henne参数化方法,选取14个设计变量来确定翼型,其中7个设计变量表示翼型厚度分布,另外7个设计变量表示翼型弯度分布。气动特性分析计算的高精度模型采用N-S雷诺平均方程计算绕翼型流场,湍流模型为S-A,网格采用非结构网格。为了比较气动优化结果,分别将Kriging代理模型与粒子群优化算法结合、Kriging自适应代理模型与粒子群优化算法结合、SVR代理模型与粒子群优化算法结合、SVR自适应代理模型与粒子群优化算法结合以及高精度模型与粒子群优化算法结合。其中,种群规模为40,进化代数为30代。粒子群优化算法中惯性权重因子采用线性递减策略[15],从0.9递减到0.4,c1=c2=2。选取150个初始样本点,添加50个样本点建立Kriging和SVR自适应代理模型;为了进行比较,另选取200个点建立Kriging和SVR代理模型。气动优化结果如下所示:
1)基于Kriging自适应代理模型的翼型气动优化设计结果
2)基于SVR自适应代理模型的翼型气动优化设计结果
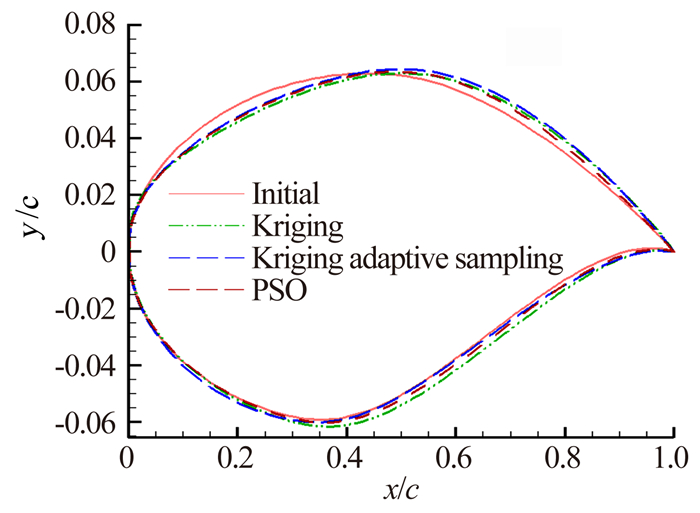
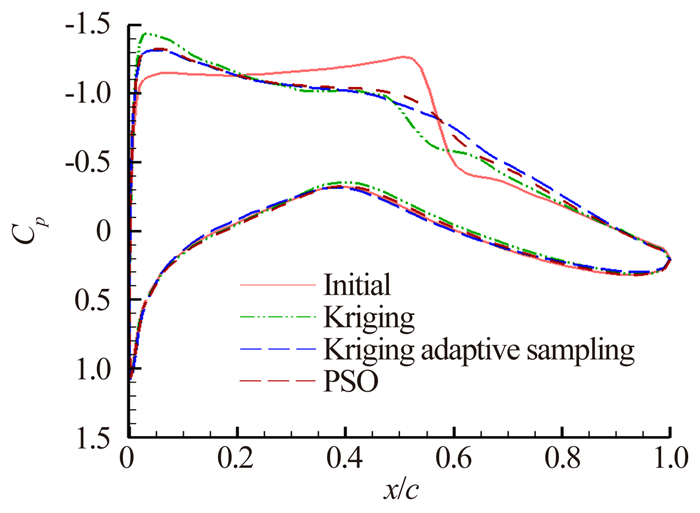
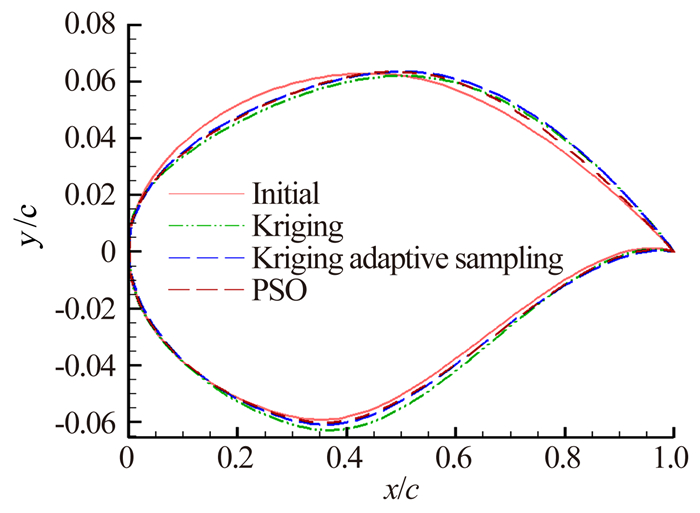
从图 14至图 17可以看出,在几何外形上,与初始翼型相比,优化翼型最大厚度位置均向后移,在气动特性上,优化翼型前缘吸力峰值增大,上表面激波强度明显减弱,采用自适应代理模型优化方法得到的翼型压力分布比一般代理模型优化方法得到的翼型压力分布更平缓一些,与高精度模型优化方法得到的翼型压力分布更相似。从表 4和表 5可以看出,基于Kriging代理模型优化方法的阻力系数减少了15.3%,基于Kriging自适应代理模型的减少了24.9%;而基于SVR代理模型的减少了19.6%,基于SVR自适应代理模型的减少了23.4%,采用高精度模型的减少了25.3%。以上结果表明,基于自适应代理模型的优化方法与基于一般代理模型的优化方法相比,在相同的样本点下,可以得到更高精度的代理模型,使得优化算法表现出较好的寻优性能,其优化结果更好。在完成翼型优化的时间上,采用代理模型花费的时间大致是使用高精度模型的一半,显著减少了气动优化设计的时间,并且能够得到与高精度模型相近的优化结果。在样本点数相同时,基于SVR代理模型的优化结果优于基于Kriging代理模型的优化结果。而在初始样本点同为150、添加样本点同为50时,基于SVR自适应代理模型的优化结果略差于基于Kriging自适应代理模型的优化结果,这可能是由于建立的这两种自适应代理模型预测能力相近,所以寻优结果没有明显差别。
| 初始 翼型 |
Kriging 代理模型 |
Kriging自适应 代理模型 |
高精度 模型优化 |
|
| Cl | 0.80 | 0.80 | 0.80 | 0.80 |
| Cd | 0.0209 | 0.0177 | 0.0157 | 0.0156 |
| tmax | 0.121 | 0.122 | 0.121 | 0.121 |
| A | 0.0778 | 0.0800 | 0.0798 | 0.0786 |
| 初始 翼型 |
SVR 代理模型 |
SVR自适应 代理模型 |
高精度 模型优化 |
|
| Cl | 0.80 | 0.80 | 0.80 | 0.80 |
| Cd | 0.0209 | 0.0168 | 0.0159 | 0.0156 |
| tmax | 0.121 | 0.122 | 0.121 | 0.121 |
| A | 0.0778 | 0.0796 | 0.0798 | 0.0786 |
|
| 图 14 优化结果翼型几何形状 Fig. 14 Optimization results of geometric shape |
|
| 图 15 优化结果翼型压力分布 Fig. 15 Optimization results of pressure distribution |
|
| 图 16 优化结果翼型几何形状 Fig. 16 Optimization results of geometric shape |

|
| 图 17 优化结果翼型压力分布 Fig. 17 Optimization results of pressure distribution |
6 小结
本文对自适应代理模型进行了详细的研究,并用典型函数对所建立的代理模型进行测试,结果表明在相同的样本点数下,自适应代理模型有更好地拟合精度,能够较好构造出实际问题相似的数学模型。并用基于自适应代理模型的优化方法对翼型进行气动优化设计,并且和基于一般代理模型的优化方法、采用高精度模型的优化方法进行了对比,结果显示基于自适应代理模型的优化方法结果与高精度模型的优化方法结果十分接近,减阻优化中阻力系数都减少10%~25%左右,比基于一般代理模型的优化方法优化效果好。由于飞机气动优化问题的复杂性,自适应代理模型的泛化能力与预测精度仍然需要提高,以及发展更加快速的算法,将成为提高优化设计效率的重要方向。
| [1] | Jouhaud J C, Sagaut P, Montagnac M, et al. A surrogate-model based multidisciplinary shape optimization method with application to a 2D subsonic airfoil[J].Computers & Fluids, 2007(36):520–529. |
| [2] |
Wang D, Xia L. Aerodynamic optimization design based on the adaptive surrogate model[D]. Xi'an: Northwestern Polytechnical University, master's thesis, 2012.(in Chinese) 王丹, 夏露.基于自适应代理模型的气动优化方法研究[D].西安:西北工业大学硕士论文, 2012. |
| [3] |
Yu Jianqiao, Wen Zhonghui, Mei Yuesong.
Tactical missile design[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2010 .
(in Chinese) 于剑桥, 文仲辉, 梅跃松, 等. 战术导弹总体设计[M]. 北京: 北京航空航天大学出版社, 2010 . |
| [4] | Sacks J, Welch W J, Michell T J, et al. Design and analysis of computer experiments[J].Statistical Science, 1989, 4(4):409–435.DOI:10.1214/ss/1177012413 |
| [5] |
Wang Xiaoguang, Xi Guang. Airfoil aerodynamic performance optimization based on kriging surrogate model[J].Acta Aeronautica Et Astronautica Sinica, 2005, 26(5):545–549. (in Chinese) 王晓锋, 席光. 基于Kriging代理模型的翼型气动性能优化设计[J]. 航空学报, 2005, 26(5) : 545–549. |
| [6] |
Zeng Huihua, Yu Xiongqing. An approach to aerodynamic shape optimization using surrogate models[J].Aeronautical Computing Technique, 2005, 35(4):84–87. (in Chinese) 曾会华, 余雄庆. 基于代理模型的气动外形优化[J]. 航空计算技术, 2005, 35(4) : 84–87. |
| [7] | McKay M D, Beckman R J, Conover W J. Acomparison of three methods for selecting values of input variables in the analysis of output from a computer code[J].Technometrics, 1979, 21(2):239–245. |
| [8] |
Li D, Xia L. Aerodynamic optimization design based on intelligent algorithms[D]. Xi'an: Northwestern Polytechnical University, master's thesis, 2011. (in Chinese) 李丁, 夏露.智能优化算法及其在气动优化设计中的应用研究[D].西安:西北工业大学硕士论文, 2011. http://mall.cnki.net/magazine/Article/YHXB200906003.htm |
| [9] | Jones D R, Schonlau M, Wilch W J. Efficient global optimization of expensive black-box functions[J].Journal of Global Optimization, 1998, 13(4):409–435. |
| [10] | Vapnik V, Chervonenkis A. A note on one class of perceptrons[J].Automation and Remote Control, 1964, 25(3):103–109. |
| [11] |
Xia L, Wang D. Aerodynamic optimization method based on Kriging adaptive surrogate model[J].Aeronautical Computing Technique, 2013, 43(1):13–17. (in Chinese) 夏露, 王丹. 基于Kriging自适应代理模型的气动优化方法[J]. 航空计算技术, 2013, 43(1) : 13–17. |
| [12] | Athanassia C, Bernhaed S, Alex J S. Experimentally optimal V in support vector regression for different noise models and parameter settings[J].Neural Networks, 2004, 17:127–141.DOI:10.1016/S0893-6080(03)00209-0 |
| [13] | Hicks R M, Henne P A. Wing design by numerical optimization[J].Journal of Aircraft, 1978, 15:407–412.DOI:10.2514/3.58379 |
| [14] |
Bai Junqiang, Wang Bo, Sun Zhiwei, et al. Developing optimization design of subsonic wing with losse type of agent model[J].Journal of Northwestern Polytechnical University, 2011, 29(4):515–519. (in Chinese) 白俊强, 王波, 孙志伟, 等. 基于松散式代理模型管理框架的亚音速机翼优化设计方法研究[J]. 西北工业大学学报, 2011, 29(4) : 515–519. |
| [15] |
Duan Xiaodong, Wang Cunrui, Liu Xiangdong.
Particle swarm optimization and its application[M]. Shenyang: Liaoning University Press, 2007 .
(in Chinese) 段晓东, 王存睿, 刘向东. 粒子群算法及其应用[M]. 沈阳市: 辽宁大学出版社, 2007 . |