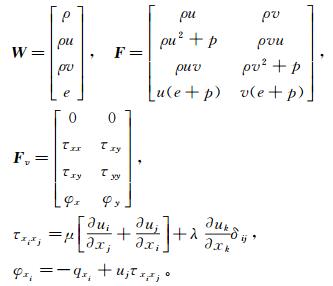由于浸没边界法(Immersed Boundary, IB)[1-4]、直角网格法[5-6]等数值模拟技术可以应用于非贴体网格,在处理复杂外形或运动边界问题时可以大大简化网格生成步骤,因而在研究和工程应用中受到越来越广泛的关注。
浸没边界法最早由Peskin[1]提出,在其发展初期,研究者借助连续力法[1]、反馈力法[3]等获得物面附近体积力的解析表达式,再借助分布函数将体积力分布在物面附近的网格单元上,通过这种间接的方式模拟物体对流动的影响。但此类方法往往受到计算稳定性的限制,且若考虑的物形为刚性物体,难以获得有效的、解析的力源项表达式。Yusof等[4]提出的离散力法扩展了浸没边界法的应用范围,提高了计算效率,大大地推进了浸没边界法的发展,尤其是在固壁问题中的应用。Fadlun等[7]研究表明,在计算浸没单元的离散力源项时,若不采用任何插值或仅采用体积分数加权平均,物面边界仅具有零阶或一阶精度;而通过插值方式获取边界附近单元的流动变量,可有效提高计算的精度。随着离散力法在研究中受到越来越广泛的关注,各种边界插值法也逐渐涌现,如线性插值[7]、双线性插值[8]、样条函数插值[4]等。
目前,离散力法研究和应用的热点主要集中在低马赫数、低雷诺数区域,这是由于常规的插值方法,如线性插值法,符合这类流动的边界层特性,因而在这类流动的模拟中应用较为成功[10];而将离散力法向可压缩流动区域推广,需要对边界附近插值法做相应的改进。Choi等[10]针对高雷诺数湍流边界层提出了考虑切向速度二次修正的指数插值法,Keistler[11]将其发展应用到超声速流动中,这也是目前较为少见的浸没边界法在可压缩流动中的应用[11-14]之一。王强等[15]采用结合了Level-Set方法的直角网格法对超声速流动问题开展了数值模拟,其中在处理物面边界时,将速度沿法向和切向分解,分别进行计算,以避免物面附近切向速度被抹平而形成数值边界层,此方法与Choi[10]用不同的插值法处理切向和法向速度的思路一致。
浸没边界法大多采用生成简便的直角网格,因而有研究者将直角网格法等采用直角非贴体网格的计算方法也归类于浸没边界法。通常所说的直角网格法,如虚拟网格法[6]、切割网格法[5]等,往往需要对边界处切割网格进行繁复处理,因此在复杂外形问题中应用较为困难。但直角网格法中某些边界处理方式,如基于虚拟网格法的曲率修正对称技术[9](Curvature Corrected Symmetry Technique, CCST)等,对浸没边界法中物面内流动变量的确定有很好的借鉴意义。
本文以离散力法为基础,从Choi等[10]提出的指数插值法出发,发展了适用于可压缩流动数值模拟的浸没边界法。文中采用NACA0012翼型在亚、跨声速段绕流问题以及超声速圆柱绕流算例对本文发展的方法进行了验证,并对该方法的模拟能力和计算精度等开展了分析。
1 数值方法 1.1 控制方程考虑体积力后,积分形式的二维可压缩N-S方程可表示为:
 (1)
(1) 其中:
式中变量ρ、p、e、T和k分别表示流体密度、静压、内能、温度和热传导系数;u、v分别为速度矢量V在直角坐标系下的速度分量;而根据Stokes假设,λ=-2μ/3;热传导项满足qxi=-k∂T/∂xi;粘性系数μ由Sutherland公式给出。
1.2 离散方法为了方便将此方法推广至三维复杂外形绕流,特别是三维复杂外形动边界问题,本文采用基于格心的有限体积法对控制方程进行离散。从后面的分析可以知道,当得到物面附近网格体积力的离散表达形式后,可在全场所有矩形网格上统一求解流动控制方程。本文计算中,采用线性MUSCL格式对网格单元内流动变量进行重构,而单元面通量采用AUSM系列格式或Roe格式计算;时间离散可采用多步Rung-Kutta方法或LU-SGS方法。
1.3 直接力法本文发展的方法基于Mohd-Yusof[4]提出的直接力方法。直接力法与Peskin[1]最初提出的连续力法不同,其主要特性是对离散后的动量方程中施加力源项,使得边界附近网格流动速度与物面的速度保持一致。
若单元i中半离散的控制方程可表示为:
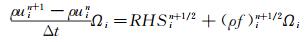 (2)
(2) 其中RHSi包含对流通量和粘性通量。根据Yusof的直接力法,体积力fi可表示为:
 (3)
(3) 这里的uBi表示根据附近流动速度和物面速度插值得到的目标点流动速度。
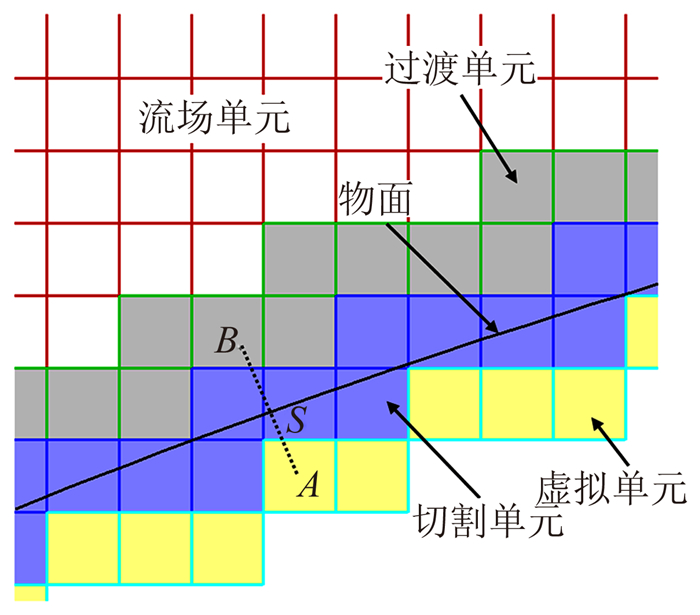
1.4 单元划分本文计算中网格体系采用直角网格,根据网格所处位置可以将计算域内的网格单元分为四种类型:流场单元、过渡单元、与物面相交的切割单元以及物面内紧邻切割单元的虚拟单元,且切割单元又被物面分为流场内和流场外两部分,图 1中所示为不同类型单元分布示意图。流场单元中直接求解不考虑体积力的流动控制方程(ρfi=0);而求解过渡单元和切割单元前,需通过插值的方式获得计算体积力所需的uBi。
|
| 图 1 单元类型示意图 Fig. 1 Schematic illustrating classification of cells |
由于切割单元被物面分割为流场内和物面内两部分,因此插值时这两部分将被区别对待。切割单元的流场内区域以及过渡单元中的速度uBi直接从邻近单元中插值(见1.6节);而切割单元物面内的部分及虚拟单元中的uBi,则需要借助虚拟网格法(见1.5节)确定。
在获得切割单元流场内区域和物面内区域两部分的流动变量后,通过体积分数确定切割单元中各参数的平均值:
 (4)
(4) 其中,q表示各流动参数,下标I和O分别表示切割单元流场内、外部分;ϕ为切割单元中流场内部分占整个网格的体积百分数。
1.5 虚拟网格法在虚拟网格法中,将各物面内节点向物面投影,找出此节点在流场中的投影点,原节点上各流动变量值根据此投影点确定。如图 1中A点位于虚拟单元的格心,B点处于流场中,且与A点关于物面对称。在本文发展的方法中,先通过插值的方式获得B点处流动速度的值,再借助Dadone等[9]提出CCST方法获得A点的值。在CCST方法中,考虑曲率影响的压力边界条件为:
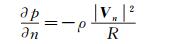 (5)
(5) 这里R是有向局部曲率半径,曲率中心在物面内部时为正,反之为负;Vn为切向速度。此外,还假设物面附近存在一个满足熵与总焓局部对称的涡流场,此时可以根据投影点B处的流动变量计算得到物面内节点A处的值:
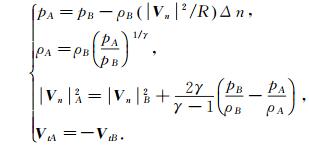 (6)
(6) 式中:Δn为线段AB的距离;Vn和Vt分别表示速度在物面法向和切向的分量。
1.6 插值方法高效、高精度的插值方式是IB方法重点关注的问题。常见的插值方法有双线性插值(三维情况为三线性插值)、最小二乘插值等;而本文研究中采用的是Choi等[10]提出的指数插值。
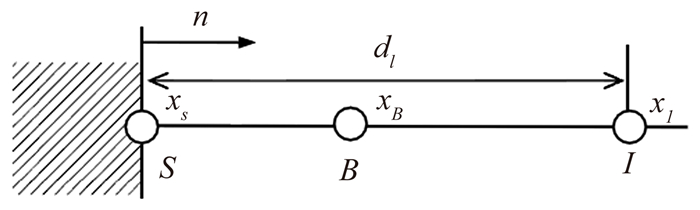
图 2中给出了插值的模版,xB为目标点,xS为目标点在边界上的投影点,xI为插值依赖点。在Choi的指数插值法中,将待求点流动速度分解为沿物面切向的速度ut, B和法向速度un, B,因而目标点处的流动速度可以用如下通用形式表示:
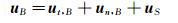 (7)
(7) 假设物面附近流动的切向速度成指数分布,而法向速度成线性分布。目标点的速度在物面切向的分量可表示为节点距物面法向距离的函数:
 (8)
(8) 其中,k为指数次数,l=dB/dI为距离参数。中括号中第二项为二阶精度的切向修正项。而目标点法向速度为:
 (9)
(9) 显然,在此方法中,指数函数的次数k的取值是与问题相关的,Choi等[10]认为,在极低雷诺数流动中Re < 1000,流动速度剖面几乎成线性分布,可以取k=1;而对于高雷诺数流动Re > 10000,可以取k=1/7或k=1/9,以避免大的流动分离。
在计算虚拟网格/切割单元物面内部分的流动变量时,还需要通过插值获得流动压力、密度等物理量。对于压力的插值,采用如下多项式关系:
 (10)
(10) 其中b=dp/dn|n=0,是与物面加速度相关的量。而目标点温度与插值依赖点温度关系根据Crocce-Busemann关系式[16]确定:
 (11)
(11) 式中:Tw为壁温,r是温度恢复因子,在层流边界层中可取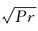
在此插值过程中,关键的插值依赖点xI的位置以及流动变量是未知的。xI点的位置在过xB的壁面法线上选取,根据各点在此方向的投影距离确定;而xI处流动变量值则通过临近单元反距离插值[10]获得。选取临近单元时,优先选择流场单元,在必须的情况下可选则过渡单元,但不选取切割单元或虚拟单元。
2 算例验证为了对本文发展方法进行验证,这里采用本文方法发展的程序对二维圆柱、翼型等外形在亚、跨、超声速阶段典型绕流算例开展了数值模拟。
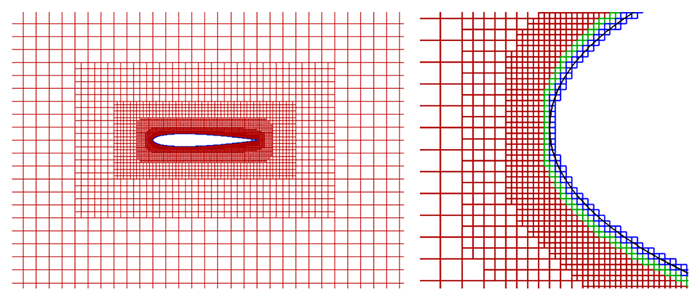
2.1 翼型绕流图 3中所示为本文中NACA0012算例计算采用的网格,在前缘细节图中可清晰分辨出流场单元(红色)、过渡单元(绿色)、切割单元(蓝色)以及物面(黑色实线)。本文计算采用的网格是经过分层加密的直角网格,计算中共采用了五套网格,以对计算结果进行网格收敛性分析。下文分析给出的流场云图及数据都来源于最密的网格。
|
| 图 3 NACA 0012翼型计算网格及前缘细节图 Fig. 3 Computational mesh and close-up for NACA0012 |
首先对NACA 0012在亚、跨声速两个状态进行了模拟,分别为Case Ⅰ: Ma=0.5,α=3.51°,Re=2×105;Case Ⅱ: Ma=0.703,α=3.22°,Re=3.75×106。
图 4中所示为Case Ⅰ算例在插值指数k=1/15时模拟得到的压力云图与马赫云图。本状态中流动处于亚声速阶段,来流绕过翼前缘后,在背风面膨胀,形成一个小的低压区。

|
| 图 4 Case Ⅰ压力云图与马赫云图 Fig. 4 Pressure and Mach contour of Case Ⅰ(k=1/15) |
图 5中给出了该算例表面压力系数分布数值模拟结果与实验数据的对比,图中黑色圆点表示实验结果,而各曲线表示切向速度分布指数k取不同值时,数值模拟得到的结果。从比较图可以清晰地看出,当k值较大(如k=1/7)时,背风面由于气流膨胀形成的吸力峰值(绝对值)明显偏小;而随着k值的不断减小,膨胀区的吸力峰值不断增大,趋近于实验结果。从图中不同k值模拟结果与实验结果的对比看,当k=1/15时,采用本文方法模拟得到的结果与实验结果最为接近。

|
| 图 5 表面压力系数数值结果与实验数据比较 Fig. 5 Comparison of CaseIpressure distribution |
图 6中给出的是当k取1和1/7时模拟得到的Case Ⅰ马赫云图。通过对不同k值模拟结果的对比容易发现,当k值较大时,背风区更容易出现分离区;而随着k值的减小,流动的分离逐渐被抑制。文献[10]中的分析认为,当k取1时,指数插值退化为线性插值,采用此指数次数模拟边界层内速度可近似为线性分布的小雷诺数流动更为合理。当采用线性分布假设边界层内速度分布时,此时流动抗逆压梯度的能力较低,更容易出现分离。

|
| 图 6 k=1和1/7时Case Ⅰ马赫云图 Fig. 6 Case ⅠMach contour at k=1 and k=1/7 |
Choi等[10]提出采用指数插值的方式近似高雷诺数边界层,文献分析认为当k=1/7或1/9时,其研究的不可压算例数值模拟结果与实验结果最为接近。我们在早期的相关研究中也有相似的结论[17];但从前面的分析可以发现,采用本文方法发展的程序在k=1/7时的模拟结果在翼型背风区会出现明显的分离区。本文方法与我们早期的研究中采用的方法主要差别在于边界附近温度分布的近似方法,在研究的早期,壁面温度分布采用等熵关系式求取;而在本文对壁面附近温度分布进行假设时,引入了Crocce-Busemann关系式。从最终的结果对比看,Crocce-Busemann关系式的引入(温度分布关系的改变),对模拟结果的影响较为显著。文献[17]中采用等熵关系式时,采用较大的k值(如1/5)仍能模拟得到较为准确的结果,显然采用此温度分布近似时对流动分离过程会有一定的抑制作用;而本文采用Crocce-Busemann关系式时,在较大k值的各模拟状态中,背风区流动分离较为明显。从前文的分析可以发现,不同温度分布近似对流动分离过程的影响还值得深入的研究。
Case Ⅱ状态为跨声速状态,虽然来流马赫数处于亚声速,但由于来流相对翼型具有一定的迎角,在翼型的背风区由于流动的膨胀出现超声速区,且在翼型背部有明显的激波存在。图 7给出了采用本文方法模拟得到的Case Ⅱ在插值指数次数k取1/15时的压力云图与马赫云图。

|
| 图 7 Case Ⅱ压力云图与马赫云图(k=1/15) Fig. 7 Pressure and Mach contour of Case Ⅱ(k=1/15) |
从图 8中k取不同值时,数值模拟结果与实验数据的对比可以发现,对于Case Ⅱ这种跨声速算例,仍是当k=1/15时数值结果与实验数据最为接近,此时模拟得到的机翼背风面激波的位置和强度与实验数据都极为吻合。

|
| 图 8 Case Ⅱ壁面压力分布数值结果与实验数据对比 Fig. 8 Comparison of the Case Ⅱ pressure distribution |
从图 9中不同k值时模拟得到的Case Ⅱ马赫云图可以发现,当k取值较小时,与Case Ⅰ中情况类似,在翼型背风区后缘会出现明显的流动分离。由于分离的出现,使得背风区前部膨胀流动的膨胀角减小,膨胀区下游的主流流动速度降低,进而使得流动膨胀引起的激波强度减弱甚至消失。因而在图 8中可以观察到,当k取1/7时,机翼背风区的吸力峰值变化光滑,此时膨胀区没有形成激波;而在k=1/9时,吸力峰值后部开始出现跳跃;在k为1/11的状态,出现了明显的激波,但此时激波强度比实验结果要弱,且位置靠前。

|
| 图 9 k=1/7和1/11时Case Ⅱ马赫云图 Fig. 9 Case Ⅱ Mach contour at k=1/7 and k=1/11 |
2.2 网格收敛性
这里选用NACA 0012翼型算例对本文方法的网格收敛性开展研究。如前所述,本文研究过程中共采用了五套计算网格。第一套(最粗)网格计算域为100c×100c,第一层网格为50×50,之后在物面附近进行了七次分层加密。第二~五套网格由前一套网格进行一分为四的四叉树加密得到。图 3中所示即为第五套网格的细节图。五套网格总的网格数及最小网格的尺度如表 1所示。
| 编号 | 网格数 | 最小网格尺度 |
| 1 | 6300 | 1.56×10-2 |
| 2 | 16 000 | 7.8 1×10-3 |
| 3 | 49766 | 3.9 1×10-3 |
| 4 | 177 750 | 1.95×10-3 |
| 5 | 674410 | 9.77×10-4 |
在开展网格收敛性研究时,根据第四和第五套网格的模拟结果, 采用Richardson外推法[18]插值获得“精确”解。外推过程中, 以最密两套网格的数值解为基础, 对于任意的流动变量φ, 其外推解φe计算方法如下:
 (12)
(12) 这里ϕ 4是将第四套网格模拟结果通过反距离加权平均映射到第五套网格上的流场; ϕ 5即第五套网格上的模拟结果。
将“精确”解通过插值再映射到各套网格上, 可求得每套网格下模拟结果与外推“精确”解之间的误差。图 10 0中给出了两状态各流动变量误差的1范数变化曲线, 其中黑色点线和虚线为示意斜率k=1和k=2的辅助线。从各曲线与斜率辅助线的对比可以看出, 两状态中各变量在密网格情况下都能达到二阶精度。

|
| 图 10 各变量误差的1范数曲线 Fig. 10 Norm-1 curves of the variables in the two cases |
2.3 圆柱绕流
为检验本文方法对超声速流动的模拟能力,采用来流条件为Re∞=2×105,M∞=1.3和1.7的二维圆柱绕流算例进行验证。计算仍采用分层加密的非均匀直角网格。根据相关文献[13, 19]的实验和计算结果可知,这两状态中圆柱尾迹为对称的稳定涡结构,因此采用半模进行计算。计算域大小为[100d×50d](半模),第一层网格(800×400),在物面附近进行七次加密,总的计算网格约为36万。
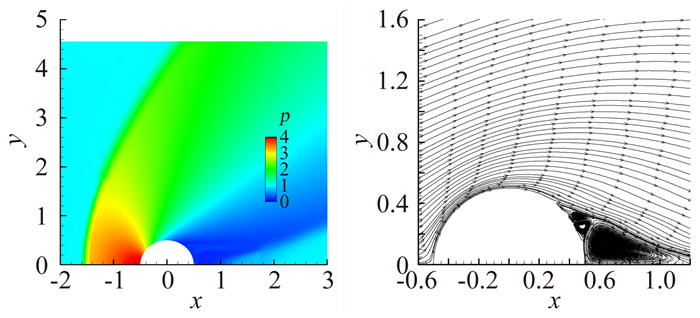
图 11和图 12分别为采用本文方法模拟得到的Ma=1.3和1.7两状态在k=1时的空间压力云图与流线图。从图中可以观察到清晰的脱体激波、流动绕过圆柱时形成的膨胀区以及尾迹区尾部拖出的膨胀激波。从图中可以看出,在超声速条件下,来流马赫数越高,其脱体激波的脱体距离越小,但波后压力越高;圆柱后尾涡的长度也随着马赫数的增大而减小。总体来说,本文方法成功地捕捉到了超声速条件圆柱绕流的各种典型流动特征。

|
| 图 11 Ma=1.3状态空间压力云图与流线图(k=1) Fig. 11 Pressure contour and streamline at Ma=1.3(k=1) |
|
| 图 12 Ma=1.7状态空间压力云图与流线图(k=1) Fig. 12 Pressure contour and streamline at Ma=1.7(k=1) |
图 13中所示是两状态在指数次数k取不同值时模拟得到的圆柱表面压力分布于实验数据的对比图。从图中可以看出,在圆柱迎风面,选取不同k值时模拟结果几乎相同,且数值模拟结果与实验结果基本吻合;但在尾迹区,尤其是分离起始位置附近,不同k值的模拟结果存在一定差异。

|
| 图 13 不同k值时圆柱表面压力分布与实验数据对比 Fig. 13 Comparison of the pressure distribution |
通过对比可以发现,在尾迹区,不同k值的模拟结果之间的差异主要在于分离起始位置的子午角不同。在分离之前,不同k值模拟结果几乎相同;如果分离时子午角增大,分离前流动速度也增大,壁面压力越低;但在分离后壁面的压力分布都将恢复到几乎恒定的水平。从对比图中可以明显看出,当k的取值较小时,其分离明显靠后;而较大k值对应的分离角明显靠前。且从两状态的模拟结果与实验数据对比看,当k=1时模拟结果与实验结果最为接近。从前文的分析可知,k取1时速度插值相当于线性近似,有利于分离流动的模拟;而k取值较小时,则会抑制分离的出现。显然,从本算例的模拟结果中可以得出类似的结论。在这种低速大分离的尾迹区域,采用线性近似的效果更好。
但从本算例的研究中又引出了新的问题,即当前方法插值次数k的取值为全场统一,这在某些流场结构相对单一的情况,如前述NACA 0012翼型绕流问题,可以得到很好的应用。但当面对的问题为混合了高/低速流动时,如何进行动态的指数插值,是需要进一步研究的课题。
3 结论本文发展了一种基于指数插值的浸没边界法。此方法在壁面附近根据速度、压力和温度等流动量自身特性,分别引入了不同的插值方式,实现了在非贴体网格上对流场进行求解的算法。
采用亚、跨声速段翼型绕流和超声速圆柱绕流算例对本文方法进行了验证,结果显示在选定插值次数k的条件下,本文方法能很好的模拟亚、跨、超声速流动问题。显然本文方法具有很强的可压缩流动模拟能力。从本文的验证过程可以发现,当k取值较大时,插值过程接近线性近似,此时在尾流等存在流动分离或低速流动区域模拟效果更佳;而k取值较小时,对激波等强压缩性区域的模拟效果更好。
从本文的分析也可以发现,在流动变量插值关系式的理论分析,以及此方法在强压缩性和大分离流动混合的复杂流动问题的应用方面还需要开展相关研究。
| [1] | Peskin C S. Flow patterns around heart valves: A numerical method[J].Journal of Computational Physics, 1972, 10:252–271.DOI:10.1016/0021-9991(72)90065-4 |
| [2] | Mittal R, Iaccarino G. Immersed boundary methods[J].Annu. Rev. Fluid Mech, 2005, 37:239–261.DOI:10.1146/annurev.fluid.37.061903.175743 |
| [3] | Goldstein D, Handler R, Sirovich L. Modeling a no-slip flow boundary with an external force field[J].Journal of Computational Physics, 1989, 105:354–366. |
| [4] | Mohd-Yusof J. Combined immersed boundaries/B-Splines methods for simulations of flows in complex geometries[R]. CTR Annual Research Briefs, NASA Ames/Stanford University, 1997. |
| [5] | Udaykumar H S, Mittal R, Rampunggoon P, et al. A sharp interface Cartesian grid method for simulating flows with complex moving boundaries[J].J. Comput. Phys, 2001, 174:345–380.DOI:10.1006/jcph.2001.6916 |
| [6] | Majumdar S, Iaccarino G, Durbin P A. RANS solver with adaptive structured boundary non-conforming grids[R]. Annu. Res. Briefs, Cent. Turbul. Res. 353-364. |
| [7] | Fadlun E A, Verzicco R, Orlandi P, et al. Combined immersed-boundary finite-difference methods for 3D complex flow simulations[J].J. Comput. Phys, 2000, 161:25–60. |
| [8] | Kim J, Kim D, Choi H. An immersed boundary finite volume method for simulations of flow in complex geometries[J].Journal of Computational Physics, 2001, 171:132–150.DOI:10.1006/jcph.2001.6778 |
| [9] | Dadone A, Grossman B. An immersed body methodology for inviscid flows on Cartesian grids[R]. AIAA-2002-1059. |
| [10] | Choi J I, Oberoi R C, Edwards J R, et al. An immersed boundary method for complex incompressible flows[J].Journal of Computational Physics, 2007, 224:757–784.DOI:10.1016/j.jcp.2006.10.032 |
| [11] | Keistler P G. An immersed boundary method for supersonic flow[R]. AIAA-2008-529. http://cn.bing.com/academic/profile?id=2321717991&encoded=0&v=paper_preview&mkt=zh-cn |
| [12] | Cho J, Chopra J, Morris P J. Immersed boundary method for compressible high-reynolds number viscous flow around moving bodies[R]. AIAA-2007-125. |
| [13] | De Palma P, De Tullio M D, Pascazio G, et al. An immersed Boundary method for compressible viscous flows[J].Computers & Fluids, 2006, 35:639–702. |
| [14] |
Liu J M. The immersed boundary method in compressible flows and its applications[D]. Nanjing university of aeronautics and astronautics, 2010. (in Chinese) 刘剑明.可压缩流体计算中的浸入边界方法及其应用[D].南京航空航天大学, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10287-1011291507.htm |
| [15] |
Wang Q, Hu X Y, Jiang Z L. A Cartesian mesh algorithm for supersonic flows around arbitrary moving bodies[J].Chinese Journal of Computational Physics, 2009, 26(4):517–526. (in Chinese) 王强, 胡湘渝, 姜宗林. 一种含运动固壁超声速流动的Descartes网格算法[J]. 计算物理, 2009, 26(4) : 517–526. |
| [16] |
Chen M Z.
Fundamentals of viscous fluid dynamics[M]. Higher education press, 2006 .
(in Chinese) 陈懋章. 粘性流体动力学基础[M]. 高等教育出版社, 2006 . |
| [17] | He Y L, Li D, Liu S, et al. An immersed boundary method based on volume fraction[C]//Asia-Pacific International Symposium on Aerospace Technology, 2014, Shanghai. |
| [18] |
Chen J Q, Zhang Y R. Verification and validation in CFD based on the Richardson extrapolation method[J].Acta Aerodynamica Sinica, 2012, 30(2):176–183. (in Chinese) 陈坚强, 张益荣. 基于Richardson插值法的CFD验证和确认方法的研究[J]. 空气动力学学报, 2012, 30(2) : 176–183. |
| [19] | Bashkin V A, Vaganov A V, Egorov I V, et al. Comparison of calculated and experimental data on supersonic flow past a circular cylinder[J].Fluid Dynamics, 2002, 37(3):473–482.DOI:10.1023/A:1019675027402 |