噪声是民用飞机适航取证的重要内容,也是目前航空领域研究的热点。随着发动机噪声的持续降低,机体噪声成为了民机噪声控制的关注重点[1-3]。襟翼边缘噪声作为机体噪声的重要组成,它的产生机理与襟翼边缘区域复杂的涡结构紧密相关[4-6]。由于上下表面压差作用,机翼下表面的边界层发生分离并上卷,形成脱落涡,并与襟翼边缘的相互作用,产生噪声[7-9]。基于对襟翼边缘噪声产生机理的分析,发展了多种通过改变襟翼边缘涡结构的降噪措施,如襟翼端板、微型片以及侧缘吹气等[10-11]。
襟翼端板作为一种简单的流动控制装置,是以小型平板的形式,安装在襟翼边缘。襟翼端板的作用原理类似于翼梢小翼,通过阻止气流在襟翼上下表面压差作用下上卷并形成强烈的上卷涡,进而降低上卷涡的强度以及上卷涡与襟翼的相互作用,抑制襟翼边缘噪声[10]。相对于其他的襟翼边缘降噪措施,襟翼端板具有结构简单、可以随襟翼展开/收起、对机翼气动外形与性能的干扰小等特点,具有较好的工程应用前景。现有的风洞试验研究已经确认[12],襟翼端板只会改变局部流动,对襟翼乃至增升装置总的升力特征不会产生显著影响。针对基于襟翼端板的多段翼噪声控制,国外开展了一些试验以及计算研究,对襟翼端板的降噪机理以及降噪效果进行了研究[13-14]。而在国内,尚未开展过相关的技术研究。
为了验证襟翼端板对襟翼边缘噪声的控制效果,设计了三种不同形式的襟翼端板,并在声学风洞中进行了试验,对有/无襟翼端板下的襟翼边缘噪声进行了测量。
1 试验模型 1.1 多段翼模型试验采用的多段翼模型为L1T2翼型[15]。模型由前缘缝翼、主翼以及后缘襟翼三部分组成,弦长为250mm,展长为375mm。为了进行襟翼边缘噪声的测试,模型的襟翼从中心分成两段,每段长度为187.5mm。试验时,通过将上半段收起、下半段展开,形成“剪刀差”构型,实现对襟翼边缘的模拟。

|
| 图 1 L1T2翼型 Fig. 1 L1T2 aerofoil |
在模型表面平齐安装两个蜂鸣器,如图 2所示,共同作为试验的校准声源对传声器阵列进行校准。蜂鸣器在额定工作电压下能够产生4800Hz、95.4dB(测量距离1m)的噪声。

|
| 图 2 多段翼模型 Fig. 2 Model of multi element wing |
1.2 襟翼端板
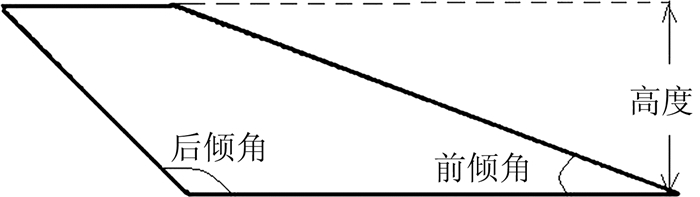
共设计有三种不同形状和尺寸的襟翼端板,如图 3所示。襟翼端板采用螺钉安装在下半段襟翼靠近中心的一端。这三种襟翼的基本尺寸参数如表 1所示。端板的厚度为2mm,前缘和边缘做倒圆处理,后缘则进行了削尖处理。

|
| 图 3 襟翼端板外形图 Fig. 3 Shape of the flap fecnes |
| 端板 | 后倾角/(°) | 前倾角/(°) | 高度/mm |
| F1 | 135 | 10 | 10 |
| F2 | 135 | 20 | 30 |
| F3 | 135 | 50 | 5 |
|
| 图 4 襟翼端板尺寸参数定义 Fig. 4 Definition of the flap fence parameters |
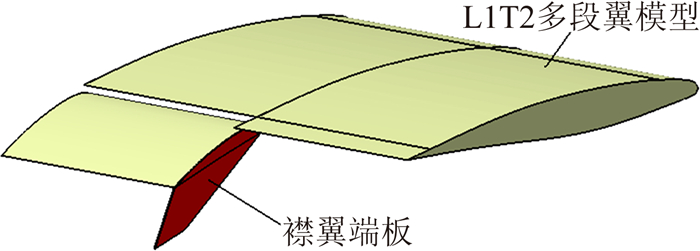
襟翼端板在模型上的安装如图 5所示,图中红色区域为襟翼端板,黄色区域为L1T2多段翼试验模型。试验过程中,模型的缝翼收起,上半段襟翼收起,下半段襟翼展开,展开角度分别为15°、30°共两个偏角。模型迎角分别为0°、3°、6°,试验风速为40m/s、60m/s、80m/s。
|
| 图 5 襟翼端板安装效果示意图 Fig. 5 Scheme of the flap fence installation |
2 试验设施与设备 2.1 声学风洞
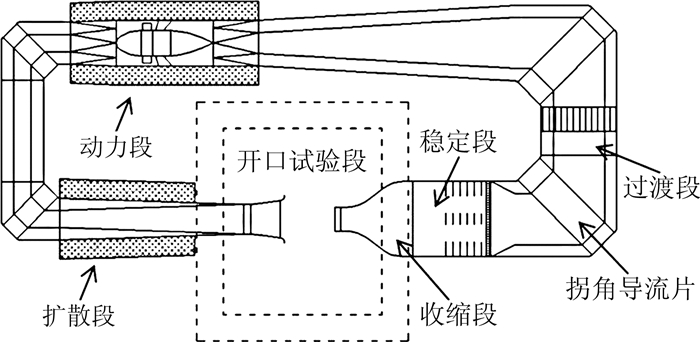
试验在中航工业空气动力研究院0.5m航空声学风洞中进行。该风洞为开口回流式风洞,试验段尺寸0.5m(宽)×0.375m(高)×1.575m(长),风速范围20~85m/s。风洞配有净空间尺寸为3.125m(长)×3.25m(宽)×2.263m(高)的全消声室,如图 6所示。消声室自由场截止频率为200Hz,风洞背景噪声≤76.8dB(A)(风速80m/s)。
|
| 图 6 0.5m航空声学风洞结构示意图 Fig. 6 Scheme of 0.5m Aeroacoustic Wind Tunnel |
2.2 翼型试验支撑装置
多段翼模型安装在翼型试验支撑装置上。支撑装置主要由支撑架、上下端板、转盘等组成,如图 7所示。上下端板的前端与试验段喷口相连,并实现对气流的约束。多段翼模型固定在上下转盘中间,通过角度块实现襟翼、缝翼偏角的变换,采用电动转盘实现迎角的自动调整。

|
| 图 7 翼型试验支撑装置 Fig. 7 Support rig of aerofoil noise testing |
2.3 测试设备
试验采用了传声器阵列以及远场传声器线阵对翼型的噪声进行测量。
试验采用自主设计的63通道传声器相位阵列进行声源定位。阵列直径1m,共有9条旋臂,每条旋臂上布置7个B&K4954传声器,如图 8所示。阵列布置在距试验段中心1.5m处,阵列面与流场方向平行。阵列中心指向风洞中心,与风洞水线等高。

|
| 图 8 63通道传声器相位阵列 Fig. 8 63-channel microphones phased array |
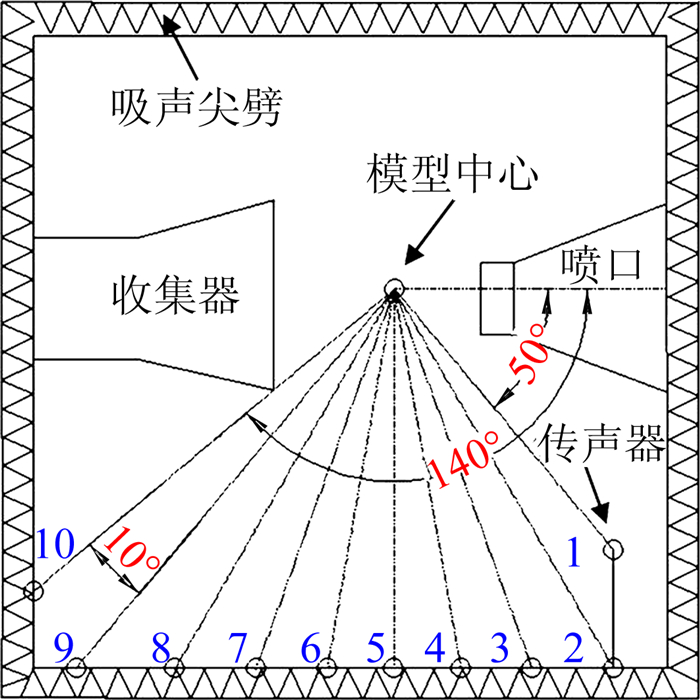
试验采用10通道传声器线阵对多段翼远场噪声进行测量,如图 9所示。传声器按等角度间隔布置,角度间隔为10°,角度范围为50°~140°(来流方向为0°),高度方向与风洞水线等高。
|
| 图 9 10通道传声器线阵 Fig. 9 10-channel microphones line array |
3 数据分析与处理方法 3.1 噪声源定位算法
试验采用基于延时-求和的波束形成算法进行噪声源定位。
传声器阵列的采样方程的向量形式为[16]:
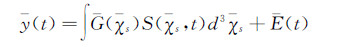 (1)
(1) 式中:y(t)为第m个阵元的采样值,G(χs)为第m个阵元确定的格林函数,E(t)为噪声项。
各个通道的采样序列将被附加一个特定的相移再进行同相叠加,使得阵列聚焦到了某一格点上。对于一个格点χb,经典算法给出的声压估计表达式如下[9]:
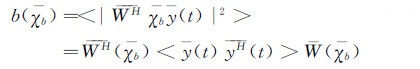 (2)
(2) 对于观测面上的每个格点分别计算上述声压估计值,利用这些数据画出的色阶图就能对主要噪声源进行定位。
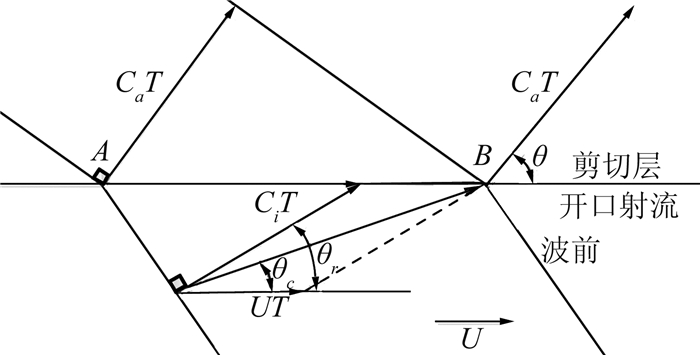
3.2 剪切层影响修正方法声波穿过开口试验段的射流剪切层时会发生折射,导致传声器阵列测得的声源位置以及远场传声器测得的指向性发生变化。为了得到正确的声源位置和指向性,需要对信号进行剪切层修正。基于Amiet理论对剪切层进行建模,假设它是无穷薄的涡流层且在两侧介质均匀,进而构建声折射的Snell定律[16]可得:
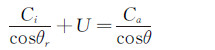 (3)
(3) 式中:Ci、Ca分别为气流内部和外部声速,θ为折射角,θr为修正角,U为开口试验段射流速度,如图 10所示。结合传播路径之间的几何关系,可以得出:
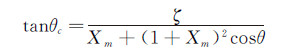 (4)
(4)
|
| 图 10 射流剪切层构建Snell定律 Fig. 10 Scheme of Snell law in the shear-layer |
其中,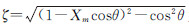
采用对指定区域进行声压级积分的方法来分析襟翼端板对襟翼边缘噪声的影响。声压级积分结果能够反映整个积分区域噪声级的强弱,排除其他声源的干扰,有利于对襟翼端板的降噪效果进行分析。图 11中虚线框所包含区域则为积分区域。整个区域为边长150mm的正方形区域,包含了襟翼边缘及襟翼端板区域。
在进行声源定位时,是将整个区域离散成多个方格进行处理的。假设积分区域中共有N个方格,其中第n个方格的声压为SPLn,可反推出对应的声压为p′n,则该区域的声压级积分方法为:
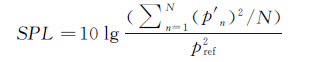 (5)
(5)
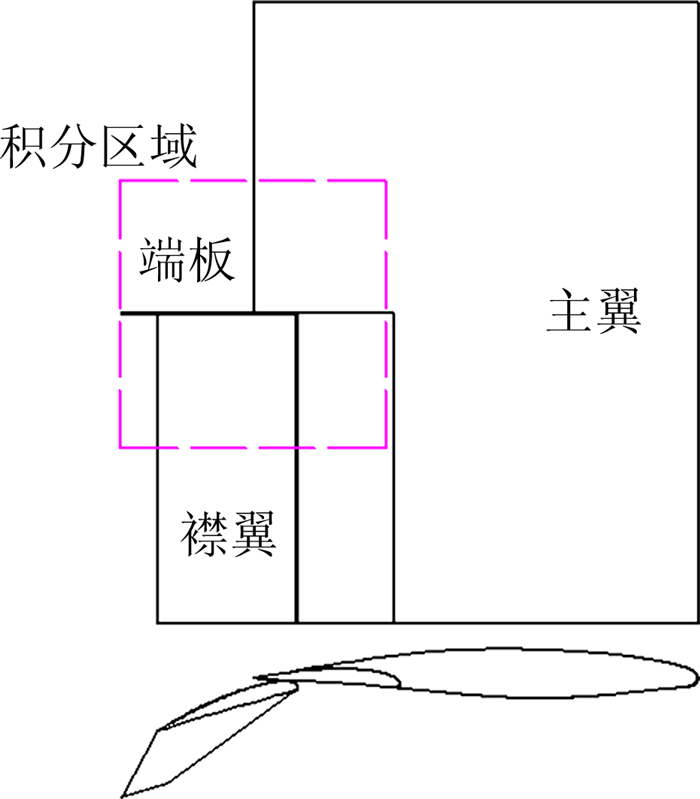
|
| 图 11 襟翼积分区域 Fig. 11 Integration area of the flap side edge |
通过对不同频率下的声源定位结果进行积分,可以得出声压级积分结果随频率的变化曲线。声压级积分结果能够反映整个积分区域噪声级的强弱,排除其他声源的干扰,有利于分析襟翼端板的降噪效果。
4 试验结果分析 4.1 剪切层影响修正试验前,采用模型表面的两个校准蜂鸣器进行传声器阵列校准以及剪切层影响修正。校准时,缝翼和襟翼均收起,以突出蜂鸣器噪声。图 12为剪切层修正前/后波束形成计算结果,黑色矩形框代表模型的实际位置,两个黑色圆点代表两个校准蜂鸣器的实际位置,红色区域代表经过波束形成分析得到的“噪声源”位置。结果表明未经过剪切层修正分析得到的“噪声源”偏向流场下游,修正后的定位结果与真实位置吻合很好,说明本文的剪切层影响修正方法可行。
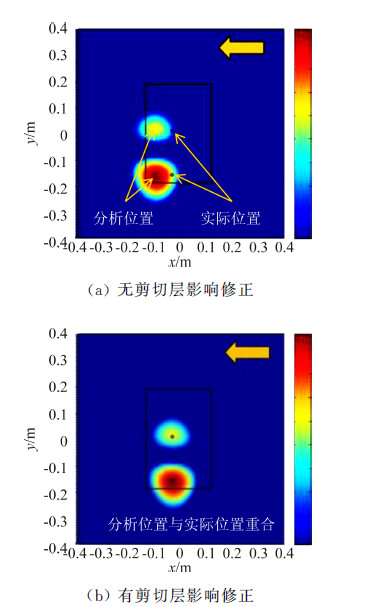
|
| 图 12 剪切层影响修正结果(U=60m/s,f=4800Hz) Fig. 12 Results of the correction of shear-layer(U=60m/s,f=4800Hz) |
4.2 远场噪声分析
多段翼模型远场噪声频谱曲线如图 13所示,测量指向角为90°。图 13中,BG为有翼型试验支撑装置时的风洞背景噪声,F0表示未安装襟翼端板,F1~F3对应前文所述的各型襟翼端板。
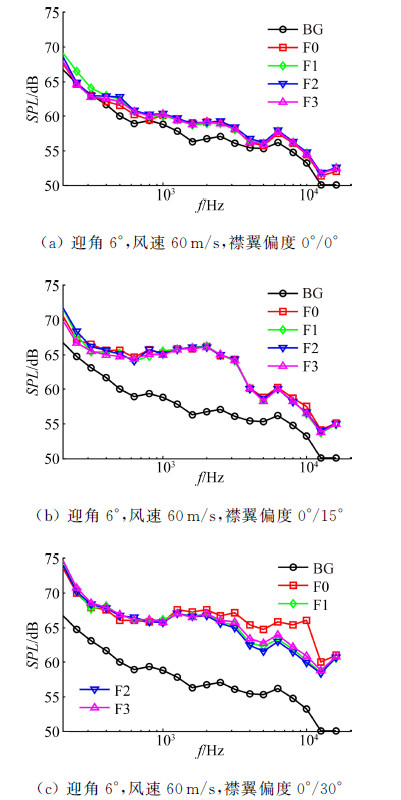
|
| 图 13 多段翼模型远场噪声频谱曲线 Fig. 13 Spectrum curves of far-filed noise |
图 13(a)是风速60m/s、多段翼襟翼全部收起时的噪声,即干净构型。分析可知,干净构型下的模型气动噪声与背景噪声相近,襟翼端板对干净构型下的模型噪声影响很小。
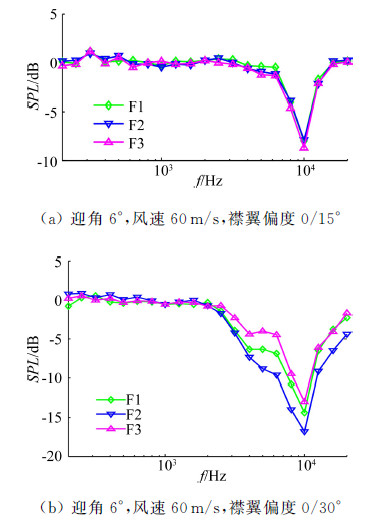
图 13(b)给出了风速60m/s、襟翼偏角为0°/15°(斜线前后分别表示上、下襟翼的偏角,下同)时远场噪声的频谱曲线。分析可知,下襟翼展开后,多段翼模型的噪声急剧增大,部分频段相对背景噪声的增量达10dB。但在该偏角下,襟翼端板的降噪效果并不明显,只在10kHz附近略有效果。
图 13(c)给出了风速60m/s、襟翼偏角为0°/30°时远场噪声的频谱曲线。相对于0°/15°襟翼偏角,F0构型的噪声增大约3dB。此时,襟翼端板产生了明显的降噪效果,在2~20kHz均有较好的降噪效果,在10kHz附近的降噪效果最好。同时,对比不同类型的襟翼端板,发现F2端板降噪效果最好,F1端板次之,F3端板最差。
以F0构型和F2构型为对象,进一步分析不同风速(40m/s、60m/s、80m/s)下的襟翼端板的降噪效果,如图 14所示。图 14(a)给出了襟翼偏角为0°/15°不同风速下的噪声频谱,可以看出多段翼模型的噪声随着风速增大而增大,而在该襟翼偏角下,F2襟翼端板在各个风速下的降噪效果均不明显。图 14(b)给出了襟翼偏角为0°/30°下的噪声频谱。在该襟翼偏度下,F2端板的降噪效果显著提升,在2~20kHz的范围内均有着一定的降噪效果。从图中可以看出,不同风速下襟翼端板的降噪量相差不大,不同频率上的最大降噪量约6dB。
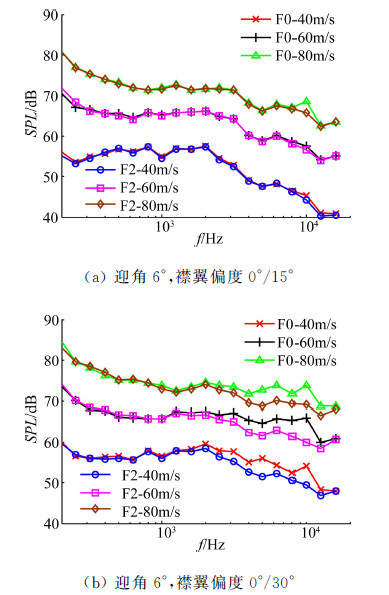
|
| 图 14 不同风速下F2端板的降噪效果 Fig. 14 Noise reduction of F2 fence under different speeds |
4.3 噪声源定位结果分析
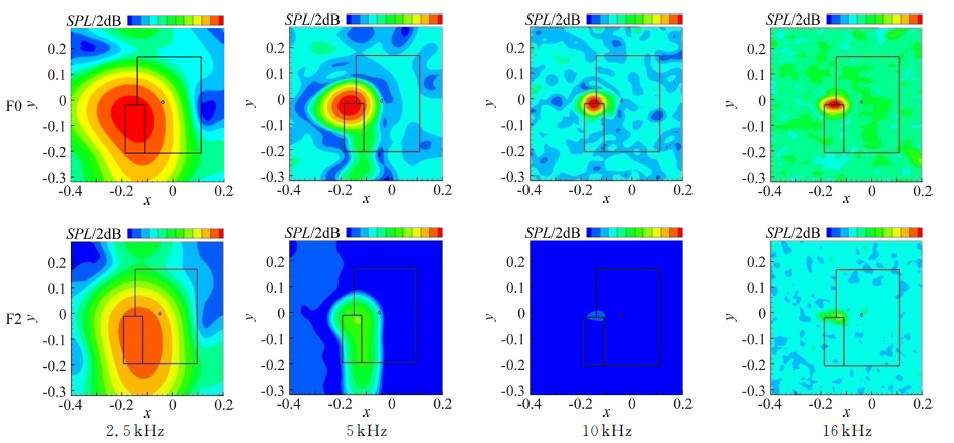
选取风速60m/s、迎角6°、襟翼偏角为0°/15°和0°/30°时F0和F2构型的声源定位结果进行对比分析,如图 15、图 16所示。图中给出了2.5kHz、5kHz、10kHz以及16kHz下1/3倍频程声源定位结果,声压级云图的动态范围均为20dB。
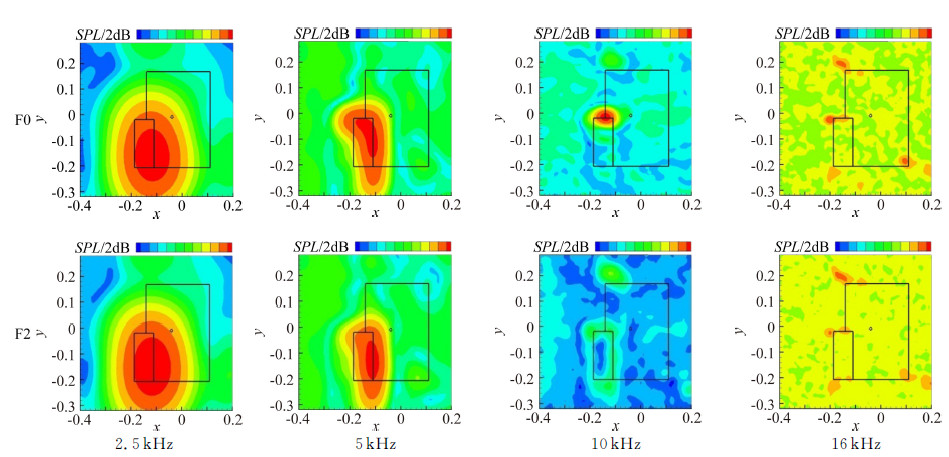
|
| 图 15 多段翼模型F0与F2构型声源定位结果(迎角6°,风速60m/s,襟翼偏角0°/15°) Fig. 15 Source location results of F0 and F2 configuration(α=6°, U=60m/s, δ=0°/15°) |
|
| 图 16 多段翼模型F0与F2构型声源定位结果(迎角6°,风速60m/s,襟翼偏角0°/30°) Fig. 16 Source location results of F0 and F2 configuration(α=6°, U=60m/s, δ=0°/30°) |
分析F0构型的声源定位结果,噪声源主要分布在襟翼腔以及襟翼边缘。频率较低时,以缝翼腔噪声为主。频率较高时,则以襟翼边缘噪声为主。其中襟翼边缘噪声主导的频率范围与襟翼偏角相关。15°襟翼偏角时,襟翼边缘噪声主导的频率范围较小,只在10kHz时是主要声源。而在30°襟翼偏角时,从5kHz到16kHz,襟翼边缘噪声均是主要声源。这也解释了15°襟翼偏角时各种襟翼端板降噪效果不明显的现象。
对比F0与F2构型声源定位结果,可以看出采用襟翼端板能够显著降低襟翼边缘区域的噪声源强度。15°襟翼偏角时,在5kHz与10kHz上显著降低襟翼边缘区域噪声,其他两个频率上襟翼边缘噪声为小量,降噪效果无法体现。30°襟翼偏角时,从2.5kHz到16kHz,襟翼端板均能显著降低襟翼边缘区域声源强度,且在总噪声上得以体现。
4.4 声压级积分结果分析对图 8所示的襟翼边缘区域进行声压级积分,得到四种构型下积分结果随频率的变化曲线,将F1、F2以及F3构型的积分结果与F0构型积分结果做差,得出了声压级积分结果降噪量随频率的变化,如图 17所示。由图 17中可以看出,襟翼端板产生的降噪量主要集中2kHz到20kHz的频率范围内,具体的频率范围与降噪量则与襟翼偏角大小相关。0°/15°偏角时,降噪频率范围是(5~16)kHz,降噪量在10kHz上达最大,约9dB,各种不同形状的襟翼端板降噪性能相近。0°/30°偏角时,降噪频率范围为2kHz到20kHz,降噪量在10kHz上达最大,约17dB,且F2端板降噪量最大,F1端板次之,F3端板降噪量最小,这也与前文所述的远场噪声降噪量相对应。
|
| 图 17 襟翼边缘区域声压级积分结果对比 Fig. 17 SPL integration results of flap side edge area |
5 结论
采用风洞试验的方法,对基于襟翼端板的襟翼边缘噪声抑制技术的降噪效果进行了验证。研究结果表明:
1) 襟翼端板能够显著降低襟翼边缘噪声,且对干净构型下的噪声影响很小,具有较好的工程应用前景。
2) 不同襟翼偏度下,由襟翼边缘产生的噪声频率范围不同,襟翼端板的降噪效果也在相应的频率范围内。襟翼偏角为0°/15°时,降噪效果集中在(5~16)kHz内;襟翼偏角为0°/30°时,降噪效果集中在(2~20)kHz内。
3) 襟翼端板降噪效果与襟翼偏角以及端板外形相关。襟翼偏角越大,降噪效果越明显;当前三种端板中,端板的尺寸越大,降噪效果越明显。
4) 由于襟翼端板自身结构简单,且只影响到翼尖的局部流动,对多段翼气动性能的影响较小。由于试验模型尺寸较小且未设计气动力测量装置,导致无法测量襟翼端板对气动性能的影响,将在后续的研究进一步完善。
| [1] | Homer G Morgan. Airframe noise-the next aircraft noise barrier[J].AlAA, :74–94. |
| [2] | Robert G Rackl. Airframe noise studies- review and future direction[R], NASA/CR 2005-213767. |
| [3] | Casalino D. Aircraft noise reduction technologies: a biblio-graphic review[J].Aerospace Science and Technology, 2008(12):1–17. |
| [4] | Hardin J C. Noise radiation from the side edges of flaps[J].American Institute of Aeronautics and Astronautics Journal, 1980, 18(5):549–552. |
| [5] | Sonya T Smith. Flap side-edge vortex bursting and airframe noise[J].AIAA, :2000–1999. |
| [6] | Crighton D G. Airframe noise, aeroacoustics of flight vehicles: theory and practice[R]. NASA RP 1258. |
| [7] | Guo Y P. Prediction of flap edge noise[J].AIAA, 1999:99–1999. |
| [8] | Brooks T F, Humphreys W M. Flap-edge aeroacoustic measurements and predictions[J].Journal of Sound and Vibration, 2003, 261:31–74. |
| [9] | Streett C L. In search of the physics: the interplay of experiment and computation in airframe noise researche- flap-edge noise[R]. AIAA 2003-979. |
| [10] | Guo Y P. On noise reduction by flap side edge fences[J].Journal of Sound and Vibration, 2004, 277:369–390. |
| [11] | Koop L, Ehrenfried K. Reduction of flap side edge noise by active flow control[R]. AIAA 2002-2469. |
| [12] | Storms B L, Takahashi T T. Flap-tip treatments for the reduction of lift-generated noise[R]. NASA CDTM-21006, 1996. |
| [13] | Ross J C, Storms B L, Kumaga H. Aircraft flyover noise reduction using lower-surface flap-tip fences[R]. NASA CDTM-21006, 1995. |
| [14] | Koop L, Ehrenfried K. Reduction of flap side-edge noise: passive and active flow control[J].AIAA, :2004–2803. |
| [15] | Balaji R, Bramkamp F, Hesse M, et al. Effect of flap and slat riggings on 2-D high-lift aerodynamics[J].Journal of Aircraft, 2006, 43(5):1259–1271. |
| [16] | Mueller T J(Ed). Aeroacoustic measurements. Springer-Verlag[M]. 2002 . |


