目前,有关格子Boltzmann方法的文献数量是十分巨大的,出现了许多中文、英文的专著[1-11],特别还有一些在该领域中有重要影响的综述性论文[12-22],估计这种势头还会持续,在这种情况下,有必要再撰写一篇有关格子Boltzmann方法的历史性简介论文吗?这是我们写作此文首先要面对的问题。回答是肯定的,因为阅读该领域研究一些研究文献的历史评述,给作者留下的初步印象并不令人十分乐观。这里特别想强调的是:这个问题的客观存在性,并且在中文文献中更为显出。我们想详细地分析出现这种混乱现象的原因所在。事实上,目前这种不健康的状态,对于整个学科的发展是十分不利的。试想:一个初入该领域的研究者如果在总体的历史信息都不准确的情况下,能做出真正具有创新意义的工作吗?
在这种情况下,我们希望选择该领域几个具体的发展故事,厘清一些概念性的东西,试图从个人的角度强调哪些作者的工作真正是具有开创性的意义。限于篇幅,这里仅仅给出一些概貌性的介绍,放弃了一些细节,感兴趣的读者可以通过原始文献的学习得到完整的通读[23-34]。
从历史角度看,尽管格子气自动机的原型可以追溯到20世纪60年代,Broadwell离散速度模型对于气体激波结构的模拟[23],但是使得格子气自动机研究真正进入公众视野的事件却是与美国华盛顿邮报有关。在科学史上,这无疑是一件有趣的事。1985年11月19日,美国华盛顿邮报在头版报道,“在Los Alamos工作的美国和法国科学家发展了一种计算流动的新方法,初期的试验表明这种新方法比传统方法快1000倍到100万倍,专家们还说需要一些时间试验才能完成[35-36]”。
我们知道,流体力学计算特别是计算空气动力学是与原子弹、飞机导弹等国防科技研究密切相联系的,所以一般公众也会关注,这很正常。后来,我们还知道,这件事还一直为20世纪人类天才的物理学家Richard Phillips Feynman所关注。实际上从事该领域的一些顶级科学家一直与Richard Phillips Feynman有所互动[35-36]。当Stephen Wolfram等人向Richard Phillips Feynman寻求学术指教时,这位天才说了如下一段话[36]:
"We have noticed in nature that the behavior of a fluid depends very little on the nature of the individual particles in that fluid. For example,the flow of sand is very similar to the flow of water or the flow of a pile of ball bearings. We have therefore taken advantage of this fact to invent a type of ima-ginary particle that is especially simple for us to simulate. This particle is a perfect ball bearing that can move at a single speed in one of six directions. The flow of these particles on a large enough scale is very similar to the flow of natural fluids. "
上述Feynman的论断基本上从物理本质概述了该研究领域后来发展的真谛所在。
其实我们认识流体世界可以有两个极端的方式,一种是经典力学的场的方式(宏观),另一种则完全是从由Maxwell发展的分子角度去认识(微观)[37]。格子Boltzmann方法却是介于两者之间的一种认识方法,是一种介观方法。这个基本出发点使得格子Boltzmann方法与传统计算流体力学方法完全不同,并且具有如下显著的优点:
1) 内在稳定;
2) 边界条件易处理;
3) 易于并行处理,或具有天然的并行性。
正因为上述的诸多原因,使得一些人对这一新的研究领域持非常乐观的态度。比如华盛顿邮报报道的那篇论文就是以“代替Navier-Stokes方程的格子气自动机”为标题的[26],非常引人眼球。另一个令学术界关注的原因在于有人直接将这一进展与经典物理的最后一个难题——湍流的解决相关联。同样是前面提到的这篇论文,在最后作者写道:Wolfram S激起了我们的兴趣,他指出了把格点自动机作为研究湍流的一种新的可能方法。甚至有人宣称找到了湍流的Ising模型。
这种新闻媒体与科学界的互动,最终吸引各国学者对该研究领域的关注,使得该领域研究论文的引用率一直攀升,形成国际学术界的研究热点,并迅速地应用到产业界。因此,学术界需要从源头厘清格子Boltzmann方法的发展历程。在这里,我们将选择关键性的几个理论概念,希望从源头上给出简要的理论发展的脉络。
1 格子气自动机的理论结构首先理论上讨论的最重要的结构是,认为所有的格子气假想弹性碰撞粒子位于所谓的Bravais格子节点上[3-5]。这种平面Bravais格子实际上是六边形平面格子,具有较高的几何对称性,能保证四阶张量是各向同性的,这是1986年Frisch等人采用这种格子的主要原因[26]。与物理实际问题相对应的是每个节点的空间位置标识为r,而物理时间为t,只是在研究中认为它们只取离散的值。在每个节点上,应用元胞自动机的思想引入一个赋予了数学物理内容的元胞自动机,并且关键性地认为问题中包含N个全同的元胞自动机结构。每个元胞赋予一个标识其节点上对应粒子运动状态的数学结构,下面可以由此建立Boolean场量,每个通道只具有两个可能的状态:0或1,分别表示该通道要么是空的,要么被一个粒子所占有,这里需要进一步引入Pauli不相容原理:每条通道只能最多被一个粒子占有。通过这种关系建立该研究节点与邻域节点之间的关系,实际上这是相互作用的表示。
现在我们观察每个节点,引入
 (1)
(1) 这样一个b-字节的符号来表示该节点的状态。这个b-字节称为节点的Boolean状态,实际上也就是单节点的相空间。
根据前面的几何构型,在整个物理空间中,存在一个有关的b-字节的N集合,这个集合存在Nb个Boolean量,记为
 (2)
(2) 称为格子的Boolean构型。而所有的可能Boolean构型的集合Γ,称为全局相空间。
为进行数值分析,还必须给几何结构赋予一定的数据结构。实际上,对应每一个离散时间,可以通过所有节点上的通道的状态集合,可以建立节点到一个集合{0,1}的映射,这个映射称为Boolean场,并标识为n。
 (3)
(3) 对每个节点,可以写成
 (4)
(4) 这里ni(r,t)表示位于r的i通道的占有数。进一步我们想研究空间节点上占有数的时间演化行为。
对于Boolean场,引入演化算子E,定义
 (5)
(5)  (6)
(6) 这里ξ(t)表示随机量。
一般将演化算子分解成两个算子的作用:
 (7)
(7) 这里T是平移算子,C是碰撞算子,后者则是需要特别研究的对象。
为了得到一个具体的格子气碰撞算子的具体表示,首先认为对于所有节点,这种碰撞算子是等同的。这实际上是采用了同步的假设[4]。另外,理论上还要引入碰撞矩阵的概念,来标识这里的局域相互作用。碰撞矩阵记为:
 (8)
(8) 它包含了所有碰撞的信息。由于每个通道存在两个状态,而对一个节点有b个通道,所以这是一个2b×2b的方阵。每个矩阵元素表示从Boolean状态s,到另一个Boolean状态
 (9)
(9) 在上述假设下,可以得到格子气流体碰撞算子的具体表达式:
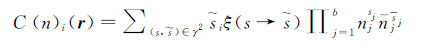 (10)
(10) 这里
特别应该注意的是上述量必须在时间t、空间r处取值,公式中没有写出。公式中的ξ(s→ )是一个2b×2b的方阵的Bernoulli随机变量(其取值为0或1),而其平均值是A(s→
)是一个2b×2b的方阵的Bernoulli随机变量(其取值为0或1),而其平均值是A(s→
 (11)
(11) 这即是格子气微观动力学基本方程。它对应于经典力学中相互作用系统的Hamilton方程,这里没有任何近似,是所有格子气动力学理论研究的出发点。
由前面的碰撞矩阵可以给出对应的细致平衡条件:
粒子碰撞过程是微观可逆的,这可以通过下面的公式表示:
 (12)
(12) 数学上讲矩阵A(s→
另一个必须给出精确定义的是系统的守恒量。
设q是所谓的观测量,如果它又是系统碰撞不变量,则有:
 (13)
(13) 使用Boolean场变量则可以表示为:
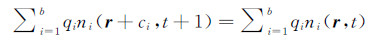 (14)
(14) 由于整个研究对象是宏观物理问题,我们必须研究整个格子网格的集团行为。而整个网格的相空间是Γ,S是一个子集,S∈Γ,由此可以引入类似于Gibbs建立的系综的概念结构,从而实现对于格子气的系综平均计算。对于每个S∈Γ,建立一种对应关系:
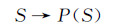 (16)
(16) 满足归一化关系
 (17)
(17) 这实际上是单粒子的概率分布函数。由此可以建立物理观测量的系综平均:
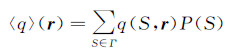 (18)
(18) 如果研究常规的观测量
 (19)
(19) 在节点r处的测量值是
 (20)
(20) 其系综平均值为:
 (21)
(21) 最后,利用前面建立的这些概念可以得到格子Liouville演化方程。当格子气系统引入概率结构后,其概率分布函数应该是时间的函数,从而构成系统的概率演化。对于格子气系统宏观的概率演化方程可以是所谓的Chapman-Kolmogorov方程:
 (22)
(22) 这个方程与连续动力学中的Liouville方程相对应。并且是严格成立的,在学术界称为格子Liouville方程。
上述的方程尽管严格成立,但是是整体性的,需要得到在每个格点上相应的概率演化方程,这个目标可以通过格点占有数的系综平均而得到。
前面占有数的演化方程(11)取系综平均可以有
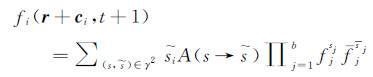 (23)
(23) 这里有
这个方程对应于连续动力学中的Boltzmann方程,不过后者是微分积分方程。经典的连续Boltzmann方程是两体碰撞的单体分布函数演化方程,公式(23)得到类似的两体相互作用的单体分布函数演化方程,所以,人们将这种离散的动力学演化方程称为格子Boltzmann方程(Lattice Boltzmann Equation,简称LBE)。
逻辑上讲,完整的对应关系还应该包括连续动力学中的细致平衡,碰撞守恒量和所谓的H-定理。
在大多数物理问题中,我们关心系统在平衡态附近的性态,这就需要研究格子气系统的平衡分布问题。在连续动力学中这是对应的Maxwell分布。可以证明:对应于格子气则平衡态分布为Fermi-Dirac分布。
平衡态的宏观态由平衡分布函数fi(eq)确定是一个重要的理论问题,一般可以采用约束变分方法,事实上在后面Koelmann的进展中实际也采用的这种方法。物理条件是在守恒量约束条件下,系统的全局熵最大[3-5]。
对格子气Liouville方程平衡解的分析表明:细致平衡条件最终可以表示为:
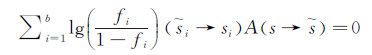 (24)
(24) 这证明观测量
设格子气系统的碰撞不变量集合为(q[k],k=1,2,…,δ),则存在如下的线性组合关系:
 (25)
(25) 从而得到平衡态分布函数:
 (26)
(26) 从统计力学我们知道上面实际是Fermi-Dirac分布。但是这里的组合系数是需要确定的,还有一个最为重要的理论问题是如何确定格子气系统的守恒量。
下面我们研究只保持质量和动量守恒的系统,宏观的变量取为密度和动量密度,即
 (27)
(27)  (28)
(28) 基本的状态选择为:所有通道为等概率的占有态,
 (29)
(29) 参数d满足
这种平衡称为低速平衡分布。
将由上述方法得到的待定系数代入分布函数的展开式,可以得到[3-5]
 (30)
(30) 其中的密度影响因子为:
从后面宏观方程的分析可以知道,这个因子引起格子气不满足Galilean不变性,其中参数的定义可以参见有关文献。
2 格子Boltzmann方法的提出从微观动力学方程通过Chapman-Enskog展开,可以得到宏观方程,这个过程一般文献中都有比较详细的过程,可以直接参考。这里我们想详细讨论有关微观动力学方程的线性化问题。这个问题所以重要的原因在于:
1) 动理学线性化本身是具有物理背景的一个问题;
2) 线性化将引入所谓的散射矩阵,其结构将直接与数值计算的稳定性相关联;
3) 对格子气系统的输运系数的计算依赖于线性化结构。
到目前为止,讨论还限于格子气流体力学的问题范畴。那么格子Boltzmann方程的概念是如何引入的呢?
我们知道对于格子气自动机,存在如下的内在缺陷:
1) 统计噪声;
2) 非Galilean不变;
3) 状态方程依赖于宏观速度,存在非物理振荡;
4) 对于单粒子格子气模型,没有独立的能量方程式。
对于格子气统计噪声问题消除,1988年McNamara和Zanetti[29],首先提出直接使用平均粒子数或粒子数分布函数代替Boolean变量进行演化,即直接按照格子Boltzmann方程计算粒子分布函数。尽管早期人们在格子气的输运系数计算中已经使用过这一方程,但是直接将此方程用于数值计算是从1988年开始的,这开创了一个新的研究方向。但是,尽管1988年McNamara和Zanetti的工作克服了格子气模型的统计噪声问题,其他问题并没有得到合理解决。1989年,Higuera和Jimenez对其进行了改进[30],他们的工作表明:计算量很大的复杂碰撞算子可以通过线性化算子逼近。线性化的手段大大地提高了计算效率,并为后来的发展奠定了重要的基础,成为了这一研究领域的一个里程碑。
从前面的分析可以得到,在引入Boltzmann假设条件下,格子气可以有Boltzmann碰撞算子
 (31)
(31) 这个算子可以在平衡态附近进行线性化处理,这里的平衡态定义如下:
 (32)
(32) 由此可以引入Boltzmann碰撞矩阵
 (33)
(33) 这个矩阵对于格子气的输运系数计算和计算的稳定性起关键性作用。可以证明,对于单粒子的格子气模型
 (34)
(34) 这里
当满足细致平衡条件时,可以写成对称的形式:
 (35)
(35) 基于对上述线化矩阵的研究,1989年Higuera,Succi和Benzi提出一种新的格子Boltzmann方程模型[31],即所谓的强化碰撞模型。他们研究的出发点是线化的格子Boltzmann方程:
 (36)
(36) 与前面的严格碰撞矩阵不同的是这里的矩阵是参数可调。
他们选取与格子气相类似的平衡态分布函数。主要的思想是希望碰撞矩阵较少地依赖于微观动力学,也就是希望更多地依赖于宏观量,使得这种选择能最终得到流体运动正确的宏观方程。
在构造强化碰撞矩阵模型时,Higuera,Succi和Benzi提出如下约束(称为HSB模型):
1) Kij是对称矩阵。
2) 各向同性,即矩阵元素仅与两个粒子速度之间的夹角有关。
3) 满足质量和动量守恒。
4) Kij是对称负定矩阵。
与前面微观动力学引入的Boltzmann碰撞矩阵比较,可以看出这里想法的合理性。首先条件1)恢复了微观碰撞矩阵的对称条件;条件2)和条件3),使得强化碰撞矩阵与微观动力学具有相同的对称。
这种方法在Frisch(1991)的建议下[34],可以通过所谓的方程投影得到宏观的流体力学方程,但是并没有使完整的Navier-Stokes方程得到恢复。这个本质困难直到1991年,才由Koelmann提出的一系列研究得到了新进展[32]。
到此,目前流行最广的LBGK方法的确立应该是呼之欲出了。实际上仔细分析,不难看到前面的HSB模型的整个理论构架实际上已经具备了LBGK方法的基本特征,唯一需要进一步挖掘的地方是碰撞矩阵。在数值计算中,对于满矩阵的处理,可以采用矩阵对角化的方法,另外在取对角化后,矩阵元取对角元的最大值也是实际应用中常用的一种快速算法。这里使用这种思维,即
 (37)
(37) 其中τ是一个无量纲参数。这种模型的碰撞算子特别简单,可以表示为
 (38)
(38) 其中fieq是一个待定的平衡分布函数。此时的碰撞算子方程即是LBGK模型所采用的形式,也称单松弛模型,τ是一个松弛时间,从而大大提高了计算效率。到此为止,可以看出还剩下一个核心问题:如何选择合适的平衡态分布函数,从该模型能推导出正确的流体运动基本方程?这个领域中这个极为关键性的一步是由Koelman(1991)完成的,因此,Koelman在1991年的工作具有开创意义,他本人应该是LBGK方法的创始人。
3 Koelman的工作一种完整的LBM至少应该包含有三种因素:1) 离散格子结构;2) 平衡分布函数;3) 动理学演化律。目前大多使用了BGK近似[32]。1991年,Koelman首次在以下的离散格子系统实现了上述的几个目标;这使得他的研究具有开创性。正如该论文中指出的那样,这里给出的是一种理论框架,而非特殊的算法。
格子速度ci的取法如下:
 (39)
(39)  (40)
(40)  (41)
(41)  (42)
(42) 这里a、b是常数,满足条件:
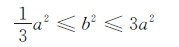 (43)
(43) 为了使用D2Q9离散格子(这种格子属性的记法是由钱跃竑等人首先引入的[33])说明问题,这里取
此时将Koelman(1991)使用的格子旋转45°,则得到标准的D2Q9离散格子,其中
 (44)
(44)  (45)
(45)  (46)
(46) 物理上的质量密度ρ,动量密度 J ,则可以由分布函数确定
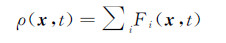 (47)
(47)  (48)
(48) 定义零速度的全局平衡分布函数Wi,则对于低马赫数流动,可以看成分布函数是对这一平衡分布的小的偏离,即有
 (49)
(49) 这里
 (50)
(50) 下面的的分析中,选择平衡态分布为Maxwell型:
 (51)
(51) 这里D是空间维度,ρ0是质量密度,m是质量,v是粒子速度,kB是Boltzmann常数,T是温度。这里对问题的四阶矩结构有
 (52)
(52)  (53)
(53)  (54)
(54)  (55)
(55)  (56)
(56) 对于D2Q9格子模型,可以得到非负解
 (57)
(57)  (58)
(58) 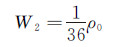 (59)
(59)  (60)
(60) 分布函数的演化按照BGK动理学方式进行,
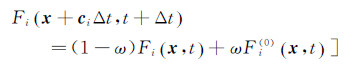 (61)
(61) 这里τ是碰撞时间,
 (62)
(62) 从上面的过程我们知道,整个的LBGK方法,将涉及到两个关键性的步骤,即权函数的计算,平衡分布函数的确定,这些理论方面的进展在Koelman(1991)开创性的工作中,都得到了具体的回答,正如作者自己所说,该论文不仅仅是给出一种具体的计算方法,而是建立了一套系统理论。令人遗憾的是,这关键性的进展在后续的大多数学者的评述中没有得到客观的体现。
问题一:权函数的计算
这里我们使用的是D2Q9几何模型,在格点上具有三个不同的速度,表 1给出详细的几何结构,以及权。
根据格点速度偶阶矩方程,可以有
零阶矩:
 (63)
(63) 二阶矩:
 (64)
(64) 四阶矩:
 (65)
(65) 由此可以得到权函数的解。
问题二:平衡分布函数的确定
Koelman首先引入了格子相对熵密度
 (66)
(66) 对于该力学系统存在两个守恒约束条件
 (67)
(67)  (68)
(68) 根据一般约束系统变分原理,可以定义系统的泛函数
 (69)
(69) 系统平衡分布函数可以从变分条件得到
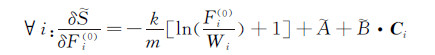 (70)
(70) 令上述变分为0,则可得到这个方程的解为
 (71)
(71) 利用动理学中的多重尺度展开,可以得到标准的Navier-Stokes方程。
从上面的工作,可以看到存在以下的不足:
1) 标准的Navier-Stokes方程仅仅是连续性方程和动量方程,而能量方程的恢复并没有得到预期的结果,使得热力学理论结构并不完善;
2) 确实Koelmann(1991)的工作,消除了影响伽利略不变性的因子,但是必须清楚地知道这里仅是针对连续性和动量方程而言的,建立在严格的群分析基础上的理论是否支持上述的结论?
在后续的论文中,我们将继续就这两个方面的问题进行探讨。
致谢: 作者对审稿人的改进意见表示衷心的感谢!| [1] | Rothman D, Zaleski S. Lattice gas cellular automata: simple models of complex hydrodynamics[M]. Cambridge University Press, 1997 . |
| [2] | Chopard B, Droz M. Encyclopedia of complexity and systems science[M]. Cambridge University Press, 1998 . |
| [3] | Wolf G D. Lattice-gas cellular automata and lattice Boltzmann models[M]. Berlin: Springer-Verlag, 2000 . |
| [4] | Rivet J P, Boon J P. Lattice gas hydrodynamics[M]. Cambridge University Press, 2001 . |
| [5] | Succi S. Lattice Boltzmann equation for fluid dynamics and beyond[M]. Oxford: Clarendon Press, 2001 . |
| [6] | Sukop M C, D.T Thorne J. Lattice Boltzmann modeling: an introduction for geoscientists and engineers[M]. Berlin: Springer, 2005 . |
| [7] | Tsutahara M, Takada N, Kataoka T. Lattice gas and lattice boltzmann methods: new methods of computational fluid dynamics[M]. Tokyo: Corona Publishing Co. Ltd, 1999 . |
| [8] |
Li Y X, Kan L S, Chen Y P.
Lattice gas automaton[M]. Beijing: Press of Qin Hua University, Press of Guangxi Keji, 1994 .
(in Chinese) 李元香, 康立山, 陈毓屏. 格子气自动机[M]. 清华大学出版社, 广西科学技术出版社, 1994 . |
| [9] |
Guo Z L, Zheng C G.
Principal and applications of the lattice Boltzmann methods[M]. Beijing: Science Press, 2009 .
(in Chinese) 郭照立, 郑楚光. 格子Boltzmann方法的原理及应用[M]. 北京: 科学出版社, 2009 . |
| [10] |
Guo Z L, Zheng C G, Li Q.
Lattice Boltzmann methods in fluid dynamics[M]. Wuhan: Press of Hubei Science and Technology, 2002 .
(in Chinese) 郭照立, 郑楚光, 李青, 等. 流体动力学的格子Boltzmann 方法[M]. 武汉: 湖北科学技术出版社, 2002 . |
| [11] |
He Y L, Wang Y, Li Q.
Theory and appllications of lattice Boltzmann methods[M]. Beijing: Science Press, 2009 .
(in Chinese) 何雅玲, 王勇, 李庆. 格子Boltzmann 方法的理论及应用[M]. 北京: 科学出版社, 2009 . |
| [12] | Benzi R, Succi S, Vergassola M. The lattice Boltzmann equation: theory and applications[J].Physics Reports, 1992, 222(3):145–197. |
| [13] | Qian Y H, Succi S, Orszag S. Recent advances in lattice Boltzmann computing[J].Annu. Rev. Comput. Phys, 1995, 3:195–242. |
| [14] | Chen S, Doolen G D. Lattice Boltzmann method for fluid flows[J].Annu.Rev.Fluid Mech, 2003, 30(5):329–364. |
| [15] | Nourgaliev R R, Dinh T N, Theofanous T G, et al. The lattice Boltzmann equation method: theoretical interpretation, numerics and implications[J].International Journal of Multiphase Flow, 2003, 29:117–169. |
| [16] |
Zhu Z X. Lattice gas automata[J].Mechanics in Engineering, 1987, 9:1–6. (in Chinese) 朱照宣. 点格自动机[J]. 力学与实践, 1987, 9 : 1–6. |
| [17] |
Hu S Y. Linear lattice gas automata[J].Mechanics in Engineering, 1988, 10:34–37. (in Chinese) 胡守信. 线性点格自动机[J]. 力学与实践, 1988, 10 : 34–37. |
| [18] |
Qian Y H, D d'Humieres, Y Pomeau, et al. The newest development of lattice gas automaton dynamics[J].Mechanics in Engineering, 1990, 12(1):7–16. (in Chinese) 钱跃竑, D d'Humieres, Y Pomeau, 等. 格子气流体动力学及其最新进展[J]. 力学与实践, 1990, 12(1) : 7–16. |
| [19] |
Li Y X. Discrete kinetic models for simulating fluid dynamics[J].Numerical Simulations and Computer Applications, 1995(3):233–240. (in Chinese) 李元香. 模拟流体力学的离散运动论模型[J]. 数值计算与计算机应用, 1995(3) : 233–240. |
| [20] |
Cheng X L, Hu F, Zhao S N, et al. The application of lattice Boltzmann method in the atmospheric turbulence study[J].Advances in Earth Science, 2007, 22(3):29–40. (in Chinese) 程雪玲, 胡非, 赵松年, 姜金华. 格子玻尔兹曼方法在大气湍流研究中的应用[J]. 地球科学进展, 2007, 22(3) : 29–40. |
| [21] |
He Y L, Li Q, Wang Y, et al. Lattice Boltzmann method and its applications in engineering thermal physics[J].Chinese Science Bulletin, 2009(18):2638–2656. (in Chinese) 何雅玲, 李庆, 王勇, 等. 格子Boltzmann方法的工程热物理应用[J]. 科学通报, 2009(18) : 2638–2656. |
| [22] |
Xu A G, Zhang G C, Li Y J, et al. Modeling and simulation of nonequilibrum and multiphase complex systems—lattice Boltzmann kinetic theory and application[J].Progress in Physics, 2014, 34(3):136–167. (in Chinese) 许爱国, 张广财, 李英骏, 等. 非平衡与多相复杂系统模拟研究——Lattice Boltzmann动理学理论与应用[J]. 物理学进展, 2014, 34(3) : 136–167. |
| [23] | Broadwell J E. Shock Structure in a simple discrete velocity gas[J].Physics of Fluids, 1964, 7(8):1243–1247. |
| [24] | Hardy J, Pomeau Y, O de Pazzis. Time evolution of a two-dimensional model system (Ⅰ): Invariant states and time correlation functions[J].Journal of Mathematical Physics, 1973(12):1746–1759. |
| [25] | Hardy J, Pomeau Y, O de Pazzis. Molecular dynamics of a classical lattice gas: Transport properties and time correlation functions[J].Phys. Rev. A, 1976, 13:1949–1961. |
| [26] | Frisch U, Hasslacher B, Pomeau Y. Lattice-gas automata for the Navier-Stokes equation[J].Physical Review Letters, 1986, 56(14):1505–1508. |
| [27] | Wolfram S. Cellular automaton fluids I: Basic theory[J].Journal of Statistical Physics, 1986, 45:471–529. |
| [28] | Frisch U, D d'Humieres, Hasslacher B, et al. Lattice gas hydrodynamics in two and three dimensions[J].Complex Systems, 1987(4):649–707. |
| [29] | McNamara G R, Zanetti G. Use of the Boltzmann equation to simulate lattice gas hydrodynamics[J].Phys. Rev. Lett, 1988, 61:2332–2335. |
| [30] | Higuera, Jiménez. Boltzmann approach to lattice gas simulation[J].Europhys Lett, 1989, 9:663–668. |
| [31] | Higuera F J, Succi S, Benzi R. Lattice gas dynamics with enhanced collisions[J].Europhysics Letters, 1989, 9(4):345–349. |
| [32] | Koelman J M V A. A simple lattice boltzmann scheme for Navier-Stokes fluid flow[J].Europhysics Letters, 1991(6):603–607. |
| [33] | Qian Y H, D d'Humieres, Lallemand P. Lattice BGK models for Navier-Stokes equation[J].Europhysics Letters, 1992, 17(6):479–484. |
| [34] | Frisch U. Relation between the lattice Boltzmann equation and the Navier-Stokes equations[J].Physica D Nonlinear Phenomena, 1991:231–232. |
| [35] | Feynman R P. Simulating physics with computers[J].International Journal of Theoretical Physics, 1982, 21(6-7):467–488. |
| [36] | Hillis W D. Richard Feynman and the connection machine[J].Physics Today, 2008, 42(2):78–83. |
| [37] | Maxwell J C. Scientific papers Ⅱ[M]. Cambridge University Press, 1890 . |










