尽管从20世纪20年代开始,航空界就已经对结冰问题开始了研究[1],但至今飞机结冰仍然是威胁飞行安全的一个重要因素。根据美国国家运输安全委员会(NTSB)的统计,从1998至2007年间,与结冰有关的飞行事故共计564起,造成229人遇难[2]。
结冰导致飞行事故的致灾机理复杂多样,单纯地依靠风洞试验和飞行试验来研究结冰对飞行的影响无疑需要消耗大量的时间和资源。通过仿真手段对结冰后的飞行动力学特性进行研究,对于研究结冰致灾机理与防护等问题显得尤为重要。
结冰后飞行动力学仿真的关键在于结冰后气动参数的获取和估算。精度最高的是直接利用飞机结冰后的风洞试验数据和试飞过程中的参数辨识结果来得到结冰飞机在不同状态下的气动参数,再通过插值算法来获取仿真所需要的气动数据,但这种方法的工作量十分巨大,而且数据的获取需要大量的试验。
当前运用较为广泛的结冰影响模型为Bragg等[3]提出的η法,其物理意义明显、结构简单,可用于估算结冰后飞机的气动参数。Lampton等[4]提出了参数fice应用于对结冰飞机气动、操纵导数的描述。该方法欠缺精度,随意性较大,但是,可方便地应用于不同类型的飞机结冰后导数的估算。文献[5]通过对Convair 580飞机的建模研究指出,结冰气象条件的微观物理参数与结冰后气动导数的变化具有建立联系的趋势,去量纲化的参数γ有希望作为一个指标参数,去体现结冰后配平以及稳定性和操纵性导数的变化。文献[6]使用神经网络方法预测了冰型对翼型气动性能的影响,指出该方法具备替代目前的η法的潜力,能体现结冰对飞机的影响。
上述结冰后的气动力模型,对于结冰后的动力学特性研究具有重要的参考价值。但这些方法都是基于线性气动力模型的基础上进行计算的,当需要对结冰后的非线性动力学特性进行研究时,特别是针对大迎角飞行区域,则需要建立结冰对非线性气动力的影响模型。而这也正是国内外结冰研究中比较缺乏的。
文中提出了一种对结冰后非线性气动力进行建模的结冰影响模型。该模型基于η法,只是模型中针对特定气动参数的影响参数的k值并不像线性模型中那样为一个常数,而是与迎角等状态参数有关。该模型的建立,能够较为合理地反映飞机在结冰状态下的动力学特性,对于利用非线性气动力模型进行动力学仿真具有一定的指导意义。
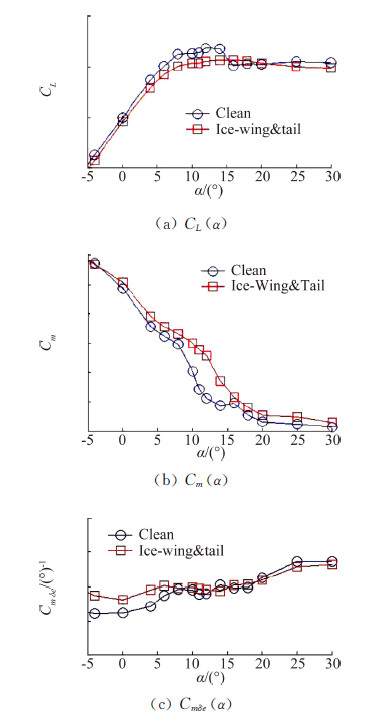
1 大迎角范围飞机结冰前后气动特性分析从公开的文献中来看,目前对飞机结冰后气动特性改变的研究大部分集中在失速前的线性阶段,对于大迎角范围内的结冰后气动力的改变,只有NASA联合部分高校和相关机构针对该领域开展了一系列的研究[7],而国内尚未有过相关的报道。本文主要在NASA典型运输机缩比模型风洞试验的结果的基础之上,对非线性结冰气动模型进行研究。图 1所示为双水獭飞机从小迎角范围到过失速区域的整个迎角范围内的结冰气动参数变化情况[8]。
|
| 图 1 结冰前后纵向气动参数的改变 Fig. 1 Changes of longitudinal aerodynamic parameters for a wide range of angle of attack |
从图 1中所示结冰前后气动参数变化情况来看,在失速前的迎角范围内,结冰后飞机的气动参数发生了明显的改变,升力系数减小,俯仰刚度Cmα及俯仰操纵力矩系数增大。而对于过失速区域,结冰前后的气动参数没有明显不同。此外在失速区域,升力系数的升力线斜率变化相对较为平坦,俯仰力矩突变开始的点右移。文献[9]中模拟翼型在不同结冰程度下的气动参数改变情况也得出了类似的结论。
从气动的角度来看,结冰对气动参数的影响主要是由于结冰破坏了翼型表面的流场[1],冰形的存在导致脱体涡的产生和耗散。然而在过失速后的飞行区域,由于迎角过大导致气流早已分离,结冰的存在与否对气动性能的影响变得不再明显。尽管公开的文献中并没有涉及飞机在大迎角范围内阻力系数的变化情况,但可以根据现有的一些小迎角范围内的数据,综合上述分析得出阻力系数在不同迎角范围内的变化[10]。
2 结冰线性气动力模型在对飞机在结冰后的动力学特性进行研究,结冰前后,运动方程的形式并没有变,只是由于结冰影响了飞机的气动特性,使得方程中的力和力矩发生了变化,此时需要将结冰对气动参数的影响考虑在内。
现有的公开文献中,对结冰气动力模型的估算,一般是基于线性稳定性导数与操纵导数进行的,即将气动力和力矩视为飞行状态和控制输入的线性函数。以纵向气动参数为例,结冰前的气动参数可表示为:
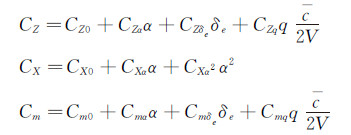 (1)
(1) 进而可得到升力系数与阻力系数:
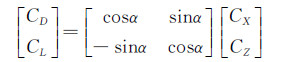 (2)
(2) 结冰对气动参数的影响主要靠改变气动导数的值体现。在众多的结冰对气动参数的影响模型中,最著名的是Bragg等人提出的结冰影响模型。按照其理论,结冰前后气动导数的关系如下:
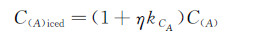 (3)
(3) 其中,C(A)与C(A)iced分别表示任意的结冰前/后飞机的性能、稳定性与控制参数或其导数。η为飞机结冰程度参数,取决于飞机的固有参数和结冰条件,具体的估算方法可参照文献[3]。对于特定的飞机,η表示飞机遭遇的结冰严重程度,其值越大,结冰后气动参数的变化也就越大,表明飞机结冰情况越严重。kCA表示结冰对飞机气动参数的影响参数,对于某架特定的飞机来说为一常值,其值可以通过数值仿真计算或飞行试验获得。
3 结冰非线性气动力模型只考虑飞机的纵向运动时,飞机的非线性气动力模型可表示为[11-12]:
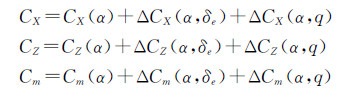 (4)
(4) 式中,C*(α)、ΔC*(α,δe)、ΔC*(α,q)等都是通过插值计算得出的。
对比第2节中的线性气动力模型,可以发现,线性气动力模型与非线性气动力模型形式上是一致的,以CZ为例,线性气动力模型中的CZ0+CZαα与非线性气动力模型中的CZ(α)对应,可粗略地认为:
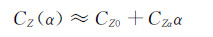 (4)
(4) 同时,线性气动力模型中的CZδe、CZq与非线性气动力模型中的ΔCZ(α,δe)、ΔCZ(α,q)对应。
因此,式(3)的结冰影响模型同样可以用来对结冰后的非线性气动力模型进行建模。对CZ,用非线性气动力模型表示的结冰后气动力可表示为:
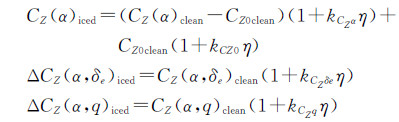 (5)
(5) 其中,下标iced表示结冰后飞机的气动参数,下标clean表示干净外形飞机的气动参数,CZ0为迎角为0°、Z轴方向的气动参数。结冰程度参数η的计算参照结冰后线性气动力模型[3,13]。
对于结冰非线性气动力模型中的kCA值,在失速区域前的取值同结冰线性气动力模型一致[3];在失速区附近kCA值应参考图 1中的变化情况进行适当的修正;当迎角大于某一阈值,kCA值取为0,即认为结冰前后的气动参数在该迎角范围视为不变。
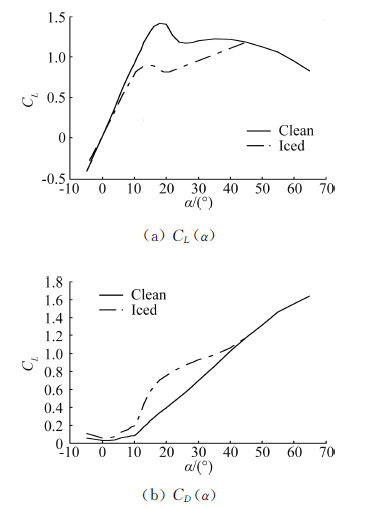
通过上述提出的结冰非线性气动力模型,得到结冰前后的升力系数、阻力系数对比曲线如图 2所示。参照文献[7,9]中风洞试验结果,与文中提出的“结冰后非线性气动力模型计算得到的结果具有相同的变化趋势”,该模型计算的结果能够满足结冰条件下飞机进入大迎角飞行区域的动态特性。
|
| 图 2 非线性气动力模型计算出的气动系数变化 Fig. 2 Comparison between clean and iced aerodynamic coefficients calculated by nonlinear icing effect model |
4 飞机纵向动力学模型
在进行飞机纵向动力学仿真时,采用以下动力学模型[11]:
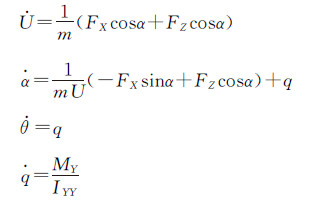 (6)
(6) 式中,U、α、θ、q分别表示来流速度、迎角、机体俯仰角、俯仰角速率。FX、FZ、MY是气动力、推力、重力的合力(矩),其计算表达式为:
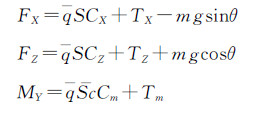 (7)
(7) 式中:q为飞机的动压,S表示机翼参考面积,c为气动弦长。TX、TZ、TM是发动机推力在机体坐标系X、Z轴方向的力以及对飞机俯仰方向力矩的分量。
5 仿真案例采用所建立的结冰后非线性气动力模型,对某型无人机在H=500m处,速度V=45m/s时,其配平特性以及飞机升降舵脉冲的动态响应来对模型的准确性进行验证。
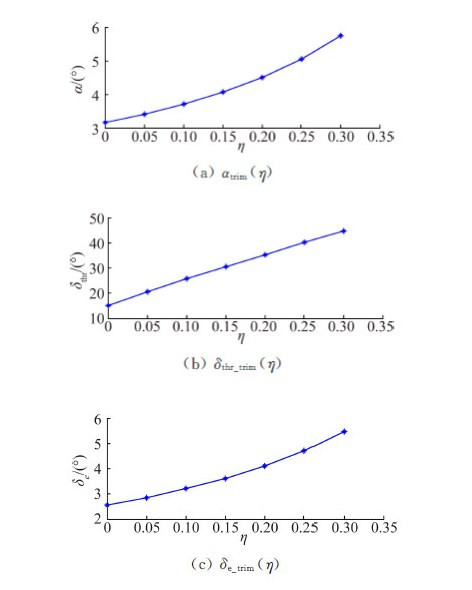
5.1 飞机结冰后配平特性分别取飞机结冰程度参数η=0、0.05、0.1、0.15、0.2、0.25、0.3,计算飞机在上述结冰程度情况下的配平状态参数及操纵输入。其计算结果如图 3所示。
|
| 图 3 飞机在不同结冰严重程度下的配平特性 Fig. 3 Trim characteristics of different icing severities |
根据仿真结果,飞机在未结冰时,平飞状态下配平参数α=3.16°,δe=2.57°;随着结冰严重程度的增大,配平迎角、油门偏度、升降舵偏角都增大。结冰后由于飞机的升力系数减小、阻力系数增大,导致飞机必须以比正常干净外形的飞机更大的迎角来维持升力,同时发动机推力必须增大以克服飞行阻力。加上结冰后升降舵的操纵效能降低,升降舵配平的偏转角度也比干净构型的飞机要大。从飞机结冰前后配平结果来看,所建立的结冰非线性气动力影响模型能够在一定程度上反映飞机在结冰后的特性。
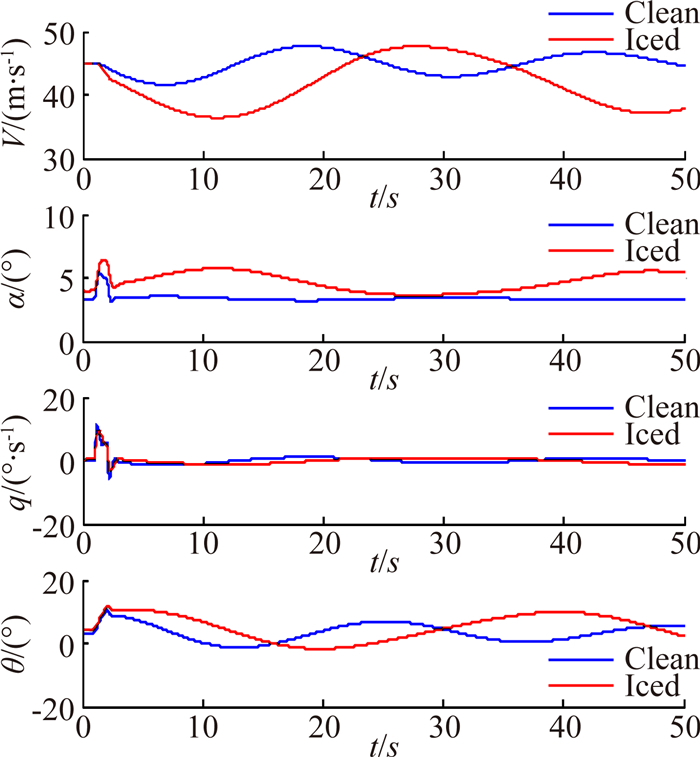
5.2 飞机结冰后纵向动态特性以飞机结冰后,巡航状态下升降舵脉冲信号作用下的动态响应,来判断结冰非线性气动力模型的正确性。假定某结冰气象条件下η=0.3,经估算,飞机的失速迎角由干净构型时的18°降低为14°。飞机保持水平直线飞行,t=5s时升降舵施以持续1s的脉冲激励,当升降舵偏度增量为-2°时,飞机的动态响应如图 4所示。
|
| 图 4 飞机在升降舵脉冲信号下的动态响应(Δδe=-2°) Fig. 4 Time history of dynamic response of elevator impulse input (Δδe=-2°) |
图 4所示的仿真结果表明,在该升降舵输入情况下,短周期模态参数迎角和俯仰角速率迅速衰减,然而结冰后飞机收敛至平衡点的速度明显下降;对于长周期模态参数速度和机体俯仰角而言,它们变化周期和幅值都有所增大。
飞机结冰后,当飞行状态处在失速区域前时,其俯仰刚度变差,加上升降舵效率下降,同样的升降舵输入舵量下,飞机的响应速度变慢[14-15],恢复至原平衡状态的能力也就越差。另一方面,结冰后会导致飞机的长周期运动模态阻尼减小,从而导致长周期模态参数的变化周期增大。从飞机动态响应的仿真结果来看,结冰会严重影响飞机的纵向操稳特性。
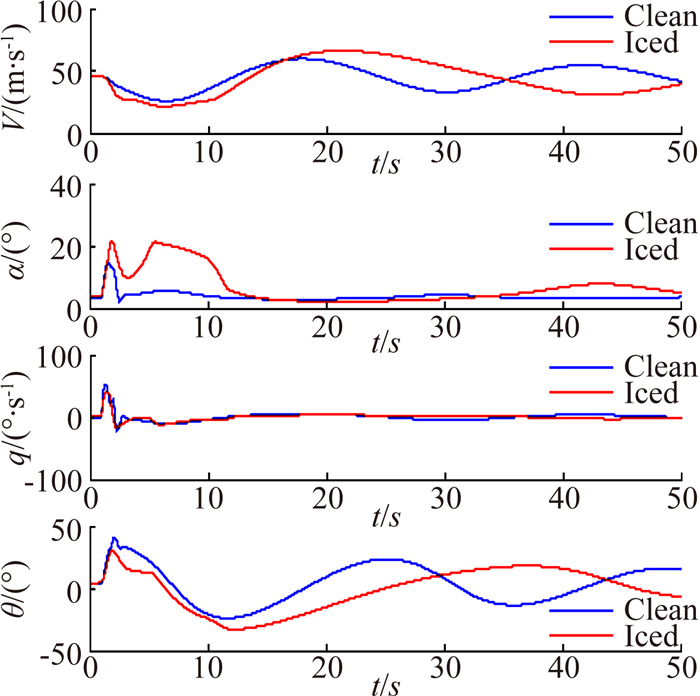
上述仿真结果,飞机动态响应的最大迎角仍处在失速迎角范围内。为研究飞机在结冰后失速及过失速区域的动态响应,将升降舵偏度增量变化为-8°,此时飞机的动态响应如图 5所示。
|
| 图 5 飞机在升降舵脉冲信号下的动态响应(Δδe=-8°) Fig. 5 Time history of dynamic response of elevator impulse input(Δδe=-8°) |
从仿真结果来看,该升降舵输入下,t=1.48s后,飞行迎角超过结冰后的失速迎角,迎角的动态响应不再是一个稳定的收敛过程,出现了不规律的波动。对于结冰线性气动力模型而言,由于其模型的有效范围仅限于失速区前的区域,当飞机迎角大于失速迎角时,线性模型已变得不再适用。此时,非线性气动力模型的作用就变得十分必要。
6 结论本文对飞机结冰非线性气动力建模和飞行动态响应特性进行了研究。建立了结冰后的气动力模型。通过对结冰后飞机的配平特性和动态响应特性分析,得出所建立的气动力模型能够反映出飞机在结冰后的飞行特性的变化,对于结冰后非线性动力学分析具有一定的借鉴意义。
需要指出的是,文中模型只是对结冰后大迎角范围气动力的一个估算模型,对于进行初步的结冰后动力学特性分析是可行的。若需要更加精确地分析动力学特性,就需要利用试验数据来进行补充。
| [1] | Bragg M B, Broeren A P, Blumenthal L A. Iced-airfoil aerodynamics[J].Progress in Aerospace Sciences, 2005, 41:323–362. |
| [2] | Dillingham G L. Preliminary information on aircraft icing and winter operations[R]. GAO-10-441T. United States Government Accountability Office, 2010. |
| [3] | Bragg M B, On T H, Merret J, et al. Effect of ice accretion on aircraft flight dynamics[R]. AIAA 2000-0360. |
| [4] | Lampton A, Valasek J. Prediction of icing effects on the lateral/directional stability and control of light airplanes[R]. AIAA 2006-6487. |
| [5] | Hui K, Wolde M, Brown A. Flight dynamics model of turboprop transport aircraft icing effects based on preliminary flight data[R]. AIAA 2005-1068. |
| [6] | Pokhariyal D, Bragg M B, Hutchison T, et al. Aircraft flight dynamics with simulated ice accretion[R]. AIAA 2001-0541. |
| [7] | Ratvasky T P, Barnhart B P, Lee S. Current methods modeling and simulating icing effects on aircraft performance, stability, control[J].Journal of Aircraft, 2010, 47(1):201–211. |
| [8] | Gingras D R. Requirements and modeling of in-flight icing effects for flight training[R]. AIAA 2013-5075. |
| [9] | Bragg M B. Aerodynamics of supercooled- large-droplet ice accretions and the effect on aircraft control[C]//Proceedings of the FAA International Conference on Aircraft Inflight Icing. Springfield, VA: 1996, 387-400. |
| [10] | Bragg M, Broeren A, Addy H, et al. Airfoil ice-accretion aerodynamics simulation[R]. AIAA 2007-085. |
| [11] | Pandita R, Chakraborty A, Seiler P, et al. Reachability and region of attraction analysis applied to GTM dynamic flight envelope assessment[C]//AIAA Guidance, Navigation, and Control Conference. AIAA 2009-6258. |
| [12] | Deters R W, Dimock G A, Selig M S. Icing encounter flight simulator[J].Journal of Aircraft, 2006, 43(5):1528–1537. |
| [13] | Pokhariyal D, Bragg M B, Hutchison T, et al. Aircraft flight dynamics with simulated ice accretion[R]. AIAA 2001-0541. |
| [14] |
Zhou L, Xu H J, Min G L, et al. Effects of ice accretion on aircraft dynamic response[J].Flight Dynamics, 2011, 29(4):32–36. (in Chinese) 周莉, 徐浩军, 闵桂龙, 等. 结冰对飞机动态响应特性的影响[J]. 飞行力学, 2011, 29(4) : 32–36. |
| [15] |
Wang M F, Wang L X, Huang C T. Computational effects of ice accretion on aircraft longitudinal stability and control[J].Journal of Beijing University of Aeronautics and Astronautics, 2008, 34(5):592–595. (in Chinese) 王明丰, 王立新, 黄成涛. 积冰对飞机纵向操稳特性的量化影响[J]. 北京航空航天大学学报, 2008, 34(5) : 592–595. |



