具有内热源的多层介质传热分析是飞机防除冰系统设计领域常见的问题。比较典型的如层合电加温风挡工作过程中内埋薄膜热源在加温控制规律作用下的非稳态传热过程分析、翼面电加热除冰系统工作过程中多层介质翼面在内埋加热电阻作用下的非稳态传热过程分析[1]。工程上可将这一类问题归结为具有内热源的多层介质非稳态传热过程分析问题。这一类问题具有以下特点:
1) 研究对象均为多层介质结构;
2) 研究对象具有时间相关的内热源;
3) 对流换热参与研究对象传热过程。
美国Keith T G、Wright W B和Yaslik A D等人在20世纪80年代到90年代结合电加热除冰系统除冰过程传热分析,对这一类问题进行了系统的试验和数值仿真研究[2-4]。国内方面,常士楠等依据电加热除冰系统结构开展具有周期性体热源的多层介质传热数值研究,并取得了一系列成果[5-7]。肖春华等对电热除冰传热特性进行了结冰风洞实验研究[8-10]。
上述学者所选择的研究对象,其热源厚度数量级通常大于10-4m,因此在热平衡方程中可以将热源定义为体积热源[2-4]。这样,热源在热平衡方程中仅需施加时间相关的加温控制规律即可方便地进行传热过程求解。对于类似于电加温风挡这类具有薄膜热源的多层介质传热问题,其热源厚度数量级通常在10-9~10-7m[11],同时热源面功率较大(如A330前风挡面功率为7450W/m2),若将其转化为体热源,则体积功率数量级可达1010~1012W/m3,导致进行数值仿真时出现非物理解。因此,无法直接依据文献[2-4]中给出的方法进行具有薄膜热源的多层介质传热特性数值仿真。
为此,本文针对某型飞机层合电加温风挡多层介质构型,构建了一种热流密度-温度边界条件。该边界条件能够依据薄膜热源的温度,实时设定薄膜热源向多层介质内外表面传递的热流,从而实现具有薄膜热源的多层介质非稳态传热耦合过程数值仿真,为具有薄膜热源的多层介质传热问题分析提供了一种可行方法 。
1 数值计算方法 1.1 计算模型图 1给出了某型飞机电加温风挡多层介质结构。各层材料名称及厚度见表 1,各材料热力参数见表 2。
|
| 图 1 电加温风挡典型构型 Fig. 1 Typical configuration of electro-thermal windshield |
| Layers | Materials | Thickness/mm |
| 1 | Glass | 3.00 |
| 2 | PU | 4.35 |
| 3 | Glass | 15.00 |
| 4 | PU | 1.50 |
| 5 | Glass | 5.00 |
| Material | k/(W·m-1K-1) | Cp/(J·kg-1K-1) | ρ/(kg·m-3) |
| Glass | 1.22 | 900 | 2490 |
| PU | 0.22 | 2080 | 1080 |
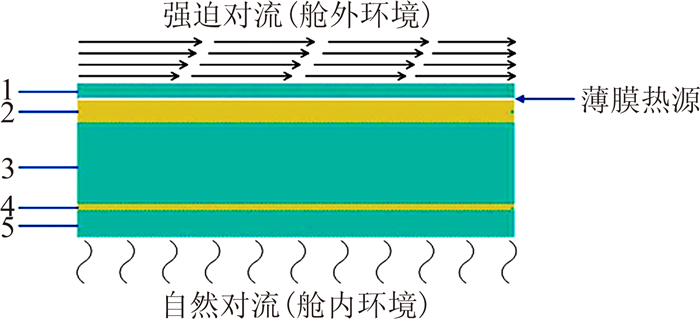
参见图 1,飞机在飞行过程中风挡主要经历舱外高速气流产生的强迫对流和舱内温差驱动的自然对流作用。风挡加温系统开启后,薄膜热源按加温控制规律将电能转化为内能,并通过图 1所示的各层介质分别向风挡外表面和内表面传递,平衡由舱外环境强迫对流换热和舱内自然对流换热带走的热量,同时保证风挡外表面温度不低于1.7℃,风挡内表面温度不低于座舱露点温度[12]。因此,电加温风挡的工作过程实质上是一种具有薄膜热源的多层介质非稳态传热过程。
在给定来流参数的条件下,风挡外表面对流换热系数主要与风挡外表面温度有关。由于风挡第1层介质热惯性很大,因此薄膜热源温度的小范围变化,对风挡外表面温度影响很小,进而对风挡外表面对流换热系数影响很小。因此,可通过给定薄膜热源的温度,采用稳态流场和传热计算确定风挡外表面对流换热系数。为减小计算误差,计算时设定风挡薄膜热源温度为其控制温度范围的平均值。风挡外表面对流换热系数确定后,将其作为边界条件施加于风挡固体区域外表面,通过非稳态传热计算确定风挡的传热特性。
本文用于进行流场计算的网格模型对应的飞机机头局部壁面网格见图 2。风挡固体区域传热计算网格模型见图 3。对流换热系数按式(1)计算[13]。
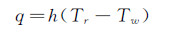 (1)
(1)
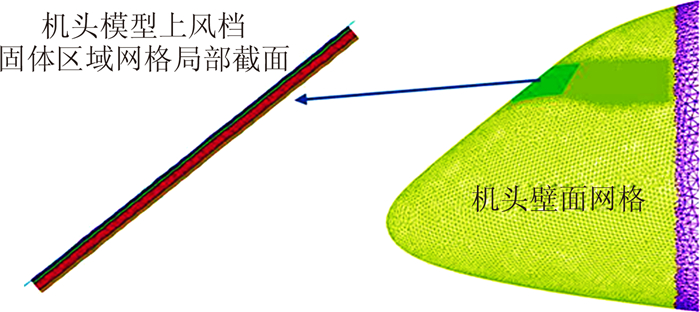
|
| 图 2 飞机机头壁面网格 Fig. 2 Wall mesh of the aircraft nose |

|
| 图 3 风挡固体区域网格模型 Fig. 3 Solid mesh of electro-thermal windshield |
1.2 控制方程
本文选用Spalart-Allmaras湍流模型结合 Navier-Stocks方程实现流体区域流场和传热的求解。输运形式的Navier-Stocks方程见式(2)[14]。式(2)中各参数含义及其数值离散和求解方法见文献[14] 。
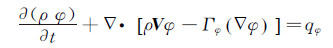 (2)
(2) 固体区域各层介质考虑为各向同性介质,其控制方程见式(3)[4]。式中脚标i表示第i层介质,见表 1。
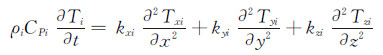 (3)
(3) 控制方程求解应用商用软件FLUENT进行,采用压力-速度耦合求解器求解,离散格式选用二阶迎风格式。
1.3 边界条件流体区域流动和传热边界见图 4,模型参考长度为43m,远场边界距模型中心为10倍参考长度。
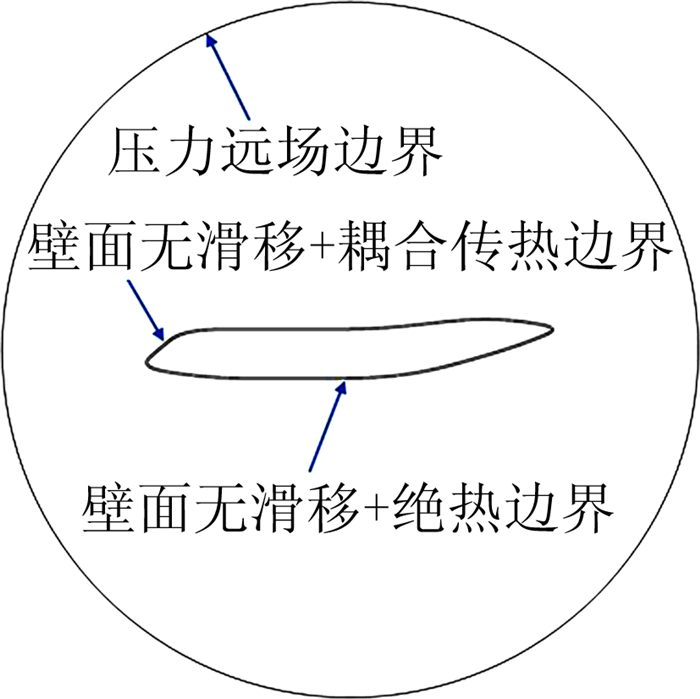
|
| 图 4 流体区域流动和传热边界示意图 Fig. 4 Boundary condition for the fluid zone |
固体区域边界设置时考虑以下假设[6]:
1) 各层介质均为各项同性介质;
2) 各层介质物性参数不随温度变化;
3) 各层介质间完全接触,不存在间隙;
4) 各层介质厚度一定。
在此基础上,薄膜热源两侧各层介质间均采用耦合传热边界[3],边界条件设置见式(4)。n表示界面的法向。
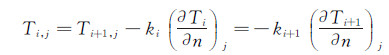 (4)
(4) 式中j表示表 1中不同介质的交界面序号,由外至内依次为0,…,5。其中第0个交界面表示固体区域外表面和流体区域的交界面,第5个界面表示固体区域内表面。
对于薄膜热源,本文构建了一种热流密度-温度边界条件,具体定义如下:
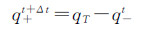 (5)
(5) 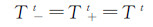 (6)
(6) 式(5)中,q-t表示t时刻薄膜热源向舱内传递的热流密度;qT表示薄膜热源的总面功率;q+t+Δt表示下一时间步(t+Δt时刻)薄膜热源向舱外传递的热流密度。式(6)中,Tt表示t时刻薄膜热源的温度;T+t表示t时刻薄膜热源靠近风挡外表面一侧的温度;T-t表示t时刻薄膜热源靠近风挡内表面一侧的温度。
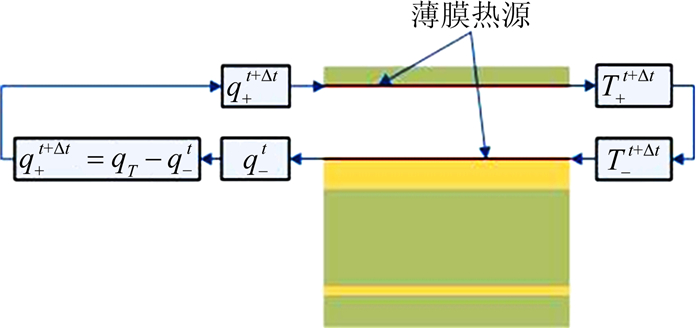
热流密度-温度边界条件的具体实施流程见图 5。在t时刻,薄膜热源的膜温为Tt,据此结合风挡内表面对流换热边界条件,可确定该时刻薄膜热源向座舱传递的热流q-t;然后依据热平衡方程,可确定t+Δt时刻薄膜热源通过外层风挡向舱外环境传递的热流q+t+Δt;在q+t+Δt和外层风挡外表面强迫对流作用下,薄膜热源获得t+Δt时刻的膜温Tt+Δt。以此类推 。
|
| 图 5 热流密度-温度边界条件 Fig. 5 HEAT FLUX-TEMPERATURE boundary condition for thin film heat source |
q-t的确定见式(7)和式(8)[1]。
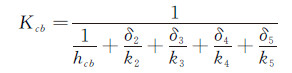 (7)
(7) 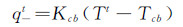 (8)
(8) 式(7)中Kcb表示薄膜热源向舱内的总传热系数;hcb表示风挡内表面自然对流换热系数,其典型值为11.375W/m2[1]。δ2、δ3、δ4、δ5分别对应表 1中2~5层介质的厚度;k2、k3、k4、k5分别对应表 1中2~5层介质的导热系数。式(8)中Tc b表示舱内温度,取舱内的最低温度21℃[12]。
2 计算条件本文选取的计算条件见表 3。薄膜热源面功率为8000W/m2,风挡各层介质初始温度设定为环境温度,攻角为0°。在风挡工作过程中,加温控制规律依据给定薄膜热源的温度范围,在薄膜热源温度上升到控温范围的上限时停止加热,在薄膜热源温度下降到控温范围的下限时启动加热。温度控制上限为43℃,温度控制下限为35℃。
| H/m | P/Pa | T/℃ | Ma | Tr/℃ | |
| Case 1 | 3000 | 70121.4 | -4.99 | 0.25 | 2.01 |
| Case 2 | 3000 | 70121.4 | -4.99 | 0.7 | 18.4 |
3 计算结果及分析
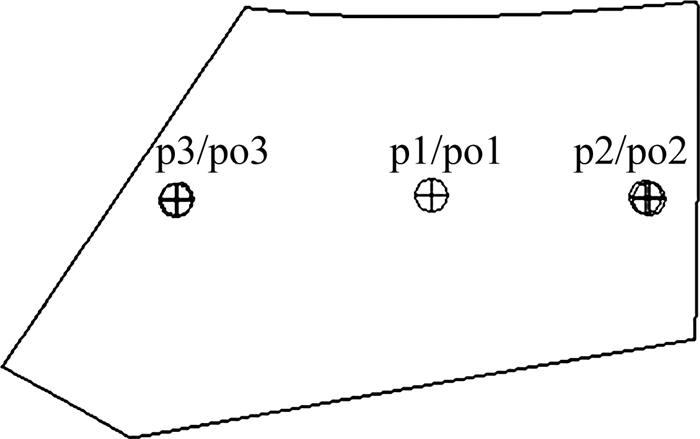
为确定风挡外表面和薄膜热源温度随时间的变化规律,分别在风挡外表面和薄膜热源所在曲面上设置3个监测点,监测点分布及编号见图 6。编号p1~p3表示薄膜热源上的监测点;编号po1~po3表示风挡外表面上的监测点。
|
| 图 6 监测点在风挡外表面和薄膜热源上的分布 Fig. 6 Probe points distribution on the outer surface and the thin film heat source |
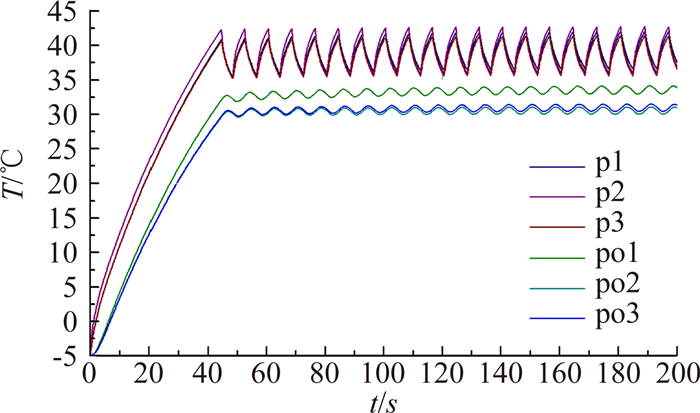
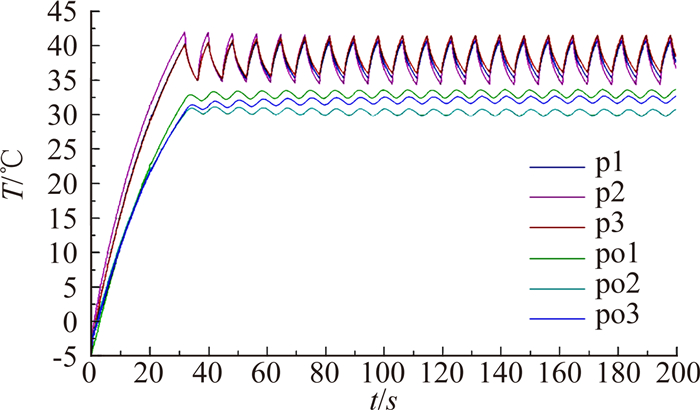
依据本文给出的方法并结合加温控制规律对表 3给出的计算状态进行仿真,得到各状态下薄膜热源监测点(p1~p3)和风挡外表面监测点(po1~po3)温度随时间的变化规律,见图 7和图 8。
1) 风挡外表面温度随薄膜热源温度波动而波动。在文中给出的薄膜热源温度控制范围内,受风挡第1层介质热惯性的影响,风挡外表面温度处于稳定波动状态后,其温度最大值和最小值之差小于1℃。
2) 在给定来流温度条件下,来流速度越大,风挡外表面壁面恢复温度越高,风挡薄膜热源温度达到稳定波动的时间越短。
对比徐佳佳等对某型飞机电加温风挡的试验结果[15]可知,本文仿真确定的温度随时间的变化曲线趋势与文献[15]中给出的试验结果相同。
4 结论本文针对某型飞机电加温风挡多层介质构型,构建了一种热流密度-温度边界条件,实现了具有薄膜热源的多层介质在对流换热作用下的非稳态传热过程数值仿真,并得到以下结论:
1) 由于薄膜热源温度在一定范围内波动可导致临近介质温度的波动,因此在分析具有非稳态工作特征的薄膜热源作用下的多层介质传热问题时,必须通过非稳态传热计算确定多层介质表面温度。
2) 在给定来流温度条件下,来流马赫数越大,壁面恢复温度越高,多层介质结构薄膜热源温度达到稳定波动的时间越短。
3) 本文构建的热流密度-温度边界条件能够有效求解具薄膜热源的多层介质传热问题。
| [1] | 裘燮纲, 韩凤华. 飞机防冰系统[M]. 北京: 航空专业教材编审组, 1985 . |
| [2] | Keith T G, DeWitt K J. Overview of numerical codes developed for predicted electrothermal de-icing of aircraft blades[R]. AIAA 1988-0288. |
| [3] | Wright W B, Keith T G. Transient two-dimensional heat transfer through a composite body with application to deicing of aircraft components[R]. AIAA 1988-0358. |
| [4] | Yaslik A D, DeWitt K J. Three-dimensional numerical simulation of electrothermal deicing systems[R]. AIAA 1991-0267. |
| [5] | 常士楠, 候雅琴, 袁修干. 周期电加热控制律对除冰表面温度的影响[J]. 航空动力学报, 2007, 22(8) : 1247–1251. |
| [6] | 常士楠, 艾素霄, 霍西恒, 等. 改进的电热除冰系统仿真[J]. 航空动力学报, 2008, 23(10) : 1753–1758. |
| [7] | 傅见平, 庄伟亮, 杨波, 等. 直升机旋翼防/除冰电加热控制律仿真[J]. 北京航空航天大学学报, 2014, 40(9) : 1200–1207. |
| [8] | 肖春华, 桂业伟, 杜雁霞, 等. 电热除冰传热特性的结冰风洞实验研究[J]. 实验流体力学, 2010, 24(4) : 21–24. |
| [9] | 肖春华, 林贵平, 桂业伟, 等. 电热除冰的热力耦合特性及其对冰层的影响研究[J]. 实验流体力学, 2012, 26(2) : 24–28. |
| [10] | 肖春华, 林贵平, 桂业伟, 等. 冰脱落对电热除冰传热特性的影响研究[J]. 空气动力学学报, 2012, 30(4) : 551–556. |
| [11] | 吴玉韬, 翁小龙, 邓龙江. 低温沉积ITO膜的透光率及电磁屏蔽特性的研究[J]. 真空科学与技术学报, 2006, 26(5) : 372–376. |
| [12] | GJB 1193-91.飞机环境控制系统通用规范[S]. |
| [13] | SAE飞机空气调节系统设计手册[M]. 北京: 国防工业出版社, 1969. |
| [14] | 易贤. 飞机积冰的数值计算与积冰试验相似准则研究[D]. 绵阳: 中国空气动力研究与发展中心, 2007. |
| [15] | 徐佳佳. 飞机风挡电加热防冰研究[D]. 南京: 南京航空航天大学, 2011. |