2. 中国航空工业第一集团公司 沈阳发动机设计研究所, 辽宁 沈阳 110015
2. Shenyang Engine Design Institute, China Aviation Industry Corporation I, Shenyang 110015, China
飞机在含有大量过冷水滴的云层中飞行时,其迎风表面会发生结冰现象。发动机进口旋转帽罩作为飞机的迎风部件,也会发生结冰现象。旋转帽罩结冰会降低发动机入口气流品质,使发动机性能降低。而且,其表面的冰如果发生脱落,被吸入发动机内部,可能会导致发动机损毁,造成重大飞行事故[1]。因此对旋转帽罩进行防冰研究很有必要。
目前飞机防冰数值模拟研究一般为稳态计算,分为空气流场求解、水滴轨迹及撞击特性求解、防冰表面热平衡分析、固体导热计算4个部分,忽略了防冰初期蒙皮表面温度较低时的防护区域的结冰及冰脱落等动态因素。但在实际过程中,为了防止系统温度过高,电加热防冰系统往往会采用间断加热的方式进行防冰[2]。因此电加热防冰是一个动态的过程,本文对旋转帽罩电热防冰瞬态过程研究,考虑了帽罩旋转以及防冰初期结冰和冰脱落对系统传热量和防冰表面温度的影响。
目前国内外对旋转帽罩防冰研究主要包括水滴撞击特性计算[3, 4]、防冰热载荷计算[5]、结冰实验和仿真计算[6-9]以及防冰实验和仿真计算[10, 11]。文献[10]对旋转帽罩热气防冰系统进行了实验及仿真研究,但其将旋转帽罩当作静止部件进行研究,没有考虑旋转对其防冰性能的影响。文献[11]对旋转帽罩热管防冰系统进行了数值计算研究,考虑了帽罩的旋转因素,但其采用的防冰传热模型中没有进行外部空气-水滴流场的计算,并且在计算外部对流换热系数时,采用的是文献[12]中的实验拟合结果,但文献[12]中的实验拟合公式只在低来流雷诺数情况下适用,对于高速飞行的飞机上的旋转帽罩并不适用。
本文基于欧拉法,建立旋转部件表面水滴撞击特性计算模型[4],求解旋转帽罩表面水滴收集系数。基于边界层积分法[13, 14]及实验拟合结果[15, 16]对旋转帽罩表面对流换热进行计算,获得旋转帽罩表面换热系数;根据改进Messinger[17] 模型建立考虑壁面热传导的传热传质方程,通过Fluent二次开发,模拟出旋转帽罩电加热防冰动态过程。
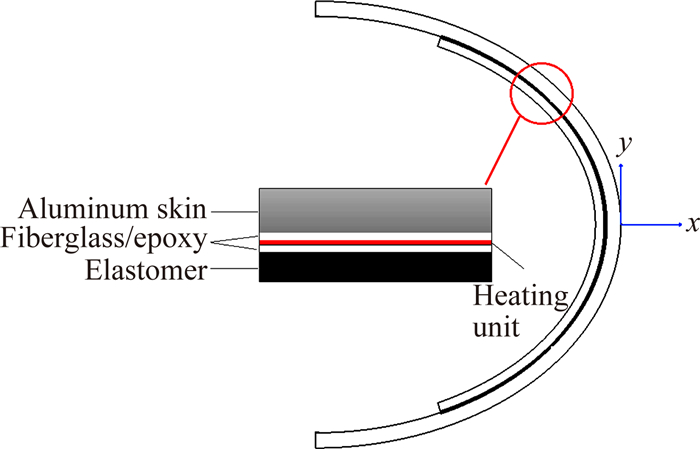
1 物理模型旋转帽罩为长轴直径0.6m,短轴直径0.44m的半椭球回转体。蒙皮为铝合金材料,厚度5mm。如图 1所示,在其内表面贴有电加热器供热,电加热器采用无间隔的加热单元。电加热器主要由环氧有机玻璃层、电加热单元、橡胶层组成,厚度分别为0.3mm、0.08mm、2.6mm。
|
| 图 1 电加热防冰物理模型示意图 Fig. 1 Electric heating anti-icing physical model |
旋转帽罩的电加热范围是在平均有效直径为40μm的水滴撞击范围的基础上,适当扩展得到的[1]。电加热防护区域在x方向(图 1中坐标系)的范围为-0.18m~0m。
2 数学模型 2.1 水滴相数学模型在结冰条件下,水滴直径一般在10-5m量级,水滴相体积分数在10-6量级。在计算中,可以对水滴场计算进行合理的假设:①水滴是球形,不发生变形和破碎;②水滴撞击到壁面之后,即被壁面捕获,不发生飞溅反弹;③水滴在空气场中处于热质平衡状态;④由于水滴所受的离心力对水滴撞击特性影响很小,忽略水滴的离心力[4]。水滴相控制方程如下[4]。
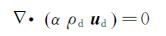 (1)
(1)  (2)
(2) 式(1)和式(2)分别为水滴相的连续性方程和动量方程,其中α是水滴体积分数;ρd 和 ud为水滴的密度和速度; ua为空气速度;K为水滴惯性系数。
水滴惯性系数表达式为:
 (3)
(3) 旋转帽罩表面局部水滴收集系数β为旋转帽罩实际水撞击量与最大可能撞击量之比,计算公式为[4]:
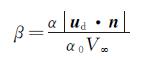 (4)
(4) 式中n为旋转帽罩壁面单元的法向单位向量,α0为远场中的水滴相体积分数。
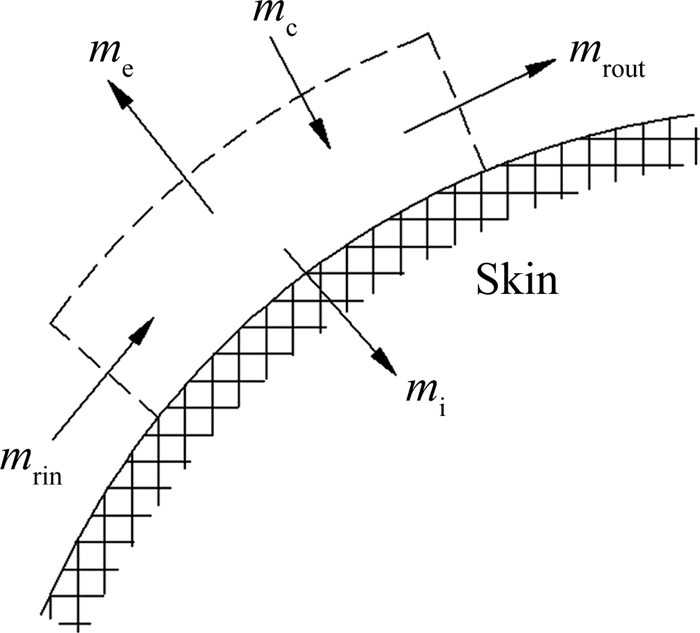
2.2 帽罩表面传热传质模型旋转帽罩表面微元控制体的质量流入流出如图 2所示,mc为微元体内收集到的水量;mrin为从上一个控制体流入的水量;me为蒸发带走的水量;mi为冻结成冰的水量(在防冰系统启动初期,帽罩表面温度低于273.15K时需要考虑,在帽罩表面温度大于273.15K时,不会发生结冰);mrout为流入到下一个控制体的水量。控制单元的质量控制方程为:
 (5)
(5)
|
| 图 2 微元体内质量平衡 Fig. 2 Mass balance in micro-unit |
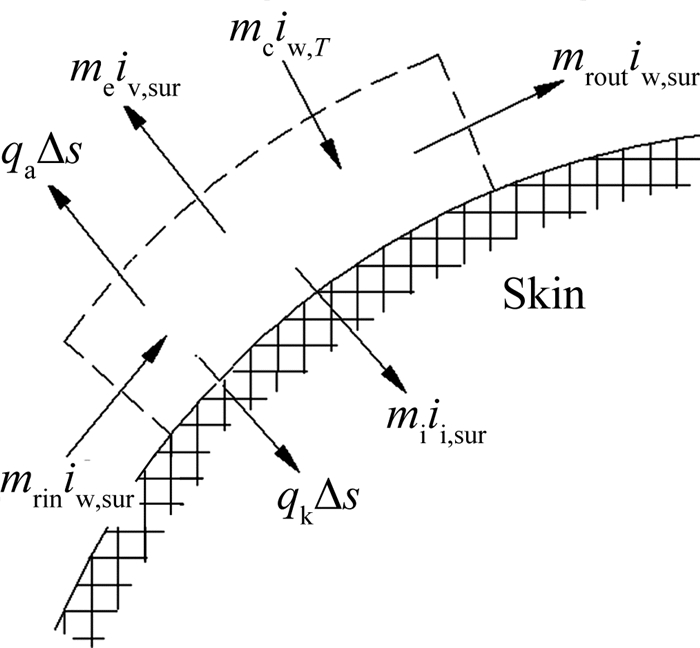
微元体内的能量的流入流出如图 3所示,mciw,T为收集的水带入的焓;mriniw,sur 为上一个控制体流入的水带入的焓;meiv,sur为蒸发的水的焓及蒸发吸热;miii,sur为冻结水的焓及冻结放热,mroutiw,sur为流出控制体水的焓。qa为对流换热热流,qk为向蒙皮导热热流,Δs为微元体的面积。其控制方程为:
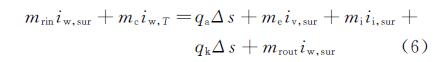 (6)
(6)
|
| 图 3 微元体内的能量平衡 Fig. 3 sEnergy balance in micro-unit |
在能量平衡方程中,水冻结放热热流的值很大,而冻结水的量主要由冻结系数决定。所谓冻结系数是指控制体中水的冻结量与控制体内总液态水量之比,如果冻结系数求解存在误差,容易导致计算发散。所以计算出准确的冻结系数很重要。
本文采用对分法迭代法求解冻结系数,在每一个防冰的计算时间步长内,都进行对分迭代,直到求出准确的冻结系数。对于某一个控制体的计算流程为:
1) 首先设定两个变量a、b,其初始值分别为0和1;
2) 令冻结系数等于b,根据上一时刻的控制体温度Tw,i-1,j,及上一个控制体流出的水量mrout,i,j-1求解质量及能量平衡方程,最终求解出当前时刻当前控制体的温度Tw,i,j;
3) 若Tw,i,j小于273.15K,则冻结系数f=1,结束迭代;若Tw,i,j大于273.15K,则令f=0.5(a+b),重新计算Tw,i,j;
4) 若Tw,i,j小于273.15K,则令a=0.5(a+b),否则令b=0.5(a+b)。
5) 令f=0.5(a+b),重新计算Tw,i,j;
6) 计算|Tw,i,j-273.15|的大小,若其大小小于微小量ε,则认为迭代收敛,退出迭代,输出冻结系数大小;若其大小大于微小量ε,则重复步骤4)、5)、6)。
本文使用Fluent软件对旋转帽罩进行固体导热计算。使用Fluent自定义函数功能将防冰表面传热传质方程写入到Fluent[18]中,在进行固体导热计算的每一步,都会进行防冰热载荷、水膜流动及结冰更新计算,并将计算得到的热载荷作为下一步固体表面计算的热边界条件,从而实现外部环境和固体热传递功能。
与静止部件相比,旋转帽罩外部是受旋转影响的复杂流场。表面附近气流在帽罩旋转作用下会发生偏转,偏转的气流又会受到离心力的影响,起到增强换热的作用[19]。针对这种复杂流动,下面将提出对流换热的计算方法。
由过增元院士提出的场协同理论[20]可知,流体的流动对于换热并不一定起到增强作用,而是与其流动方向和热传递方向的夹角有关,换热增强的能力与两者夹角的余弦值正相关。当夹角小于90°时,夹角越小,换热强度越大,当两者方向一致时达到最大。若两者速度夹角为90°时,流场的流动并不能起到增强换热的作用。
对于旋转帽罩,在其旋转时,在壁面摩擦力的作用下,帽罩壁面附近气流只会产生切向速度。而旋转帽罩表面的热传递方向为帽罩法线方向,两者的夹角为90°,由上面介绍的场协同理论可知,流体的切向速度并不能起到增强换热的作用。而旋转帽罩周围的气流所受的离心力会使气流产生径向速度,其与热传递方向的夹角在0°到90°之间,能够起到增强换热的作用。可见帽罩旋转的增强换热作用主要是由离心力引起的。所以可以认为旋转换热是具有体积力的自然对流换热[13],文献[21]中的研究也证明了这一点。
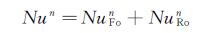 (7)
(7) 其中Nu为综合努塞尔数,NuFo、NuRo分别为强迫对流及自然对流的努塞尔数。
强迫对流换热系数的计算方法主要有雷诺比拟法及边界层积分方法。本文采用文献[13]中的边界层积分方法计算远离驻点区域的换热系数,文中不再进行介绍。由于边界积分法在对边界层厚度计算时采用的假设在驻点附近不成立,故驻点附近的换热系数采用圆柱换热公式[23]进行计算:
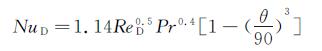 (8)
(8) 式中ReD是以旋转帽罩前缘直径为特征尺寸的雷诺数 。 由于目前没有针对旋转帽罩外形的旋转换热研究,旋转对流换热的努塞尔数近似采用圆柱旋转换热实验拟合公式[15, 16]来计算:
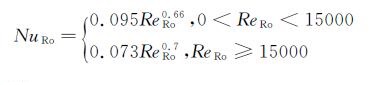 (9)
(9) 为了验证研究方法的正确性,将该方法计算的帽罩表面对流换热系数、水滴收集系数及温度结果分别与成熟的商业软件Fluent、FENSAP-ICE计算结果进行比较。计算中采用的环境温度为263.15K,环境压力101kPa,飞行速度60m/s,液态水含量1g/m3水滴直径20μm,电加热功率密度为3W/cm2。
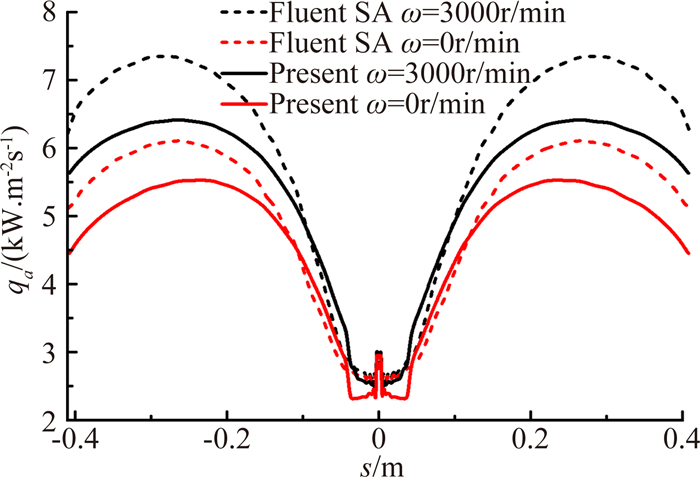
首先对对流换热热流计算结果进行比较验证,见图 4。s为驻点到表面上任一点的弧长,旋转帽罩表面为288.15K定温边界条件。从图中可以看出,本文计算结果和Fluent数值计算结果沿帽罩弧长分布趋势一致。由于冲击作用,对流换热热流在驻点处为极大值;从驻点往后,帽罩表面先为层流,后来发生转捩为湍流,换热量急剧增加;随着湍流发展,边界层厚度增厚,换热量又逐渐减小。
|
| 图 4 帽罩表面对流换热热流分布 Fig. 4 Nose cone surface convective heat transfer of heat flow distribution |
从数值计算结果和本文计算结果来看,旋转会使帽罩表面对流换热明显增强,特别是在旋转帽罩后缘,帽罩直径增大,帽罩表面附近的空气所受到的离心力增加,导致较强的换热增强。但由于方法不同,有一定的误差。
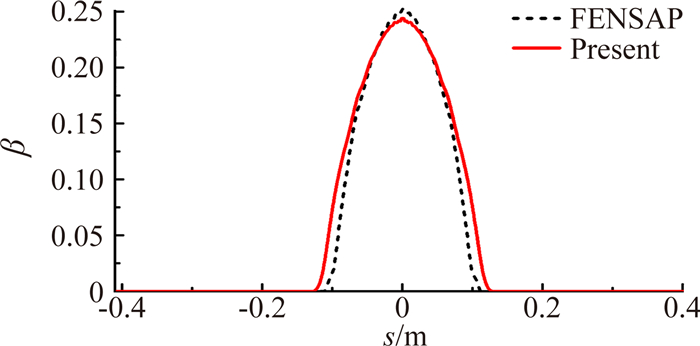
图 5是旋转帽罩表面局部水滴收集系数计算结果。可以看出,本文的计算结果与FENSAP计算结果基本吻合,说明本文的水滴收集系数计算结果是合理的。
|
| 图 5 帽罩表面局部收集系数分布 Fig. 5 Nose cone surface local collection coefficient distribution |
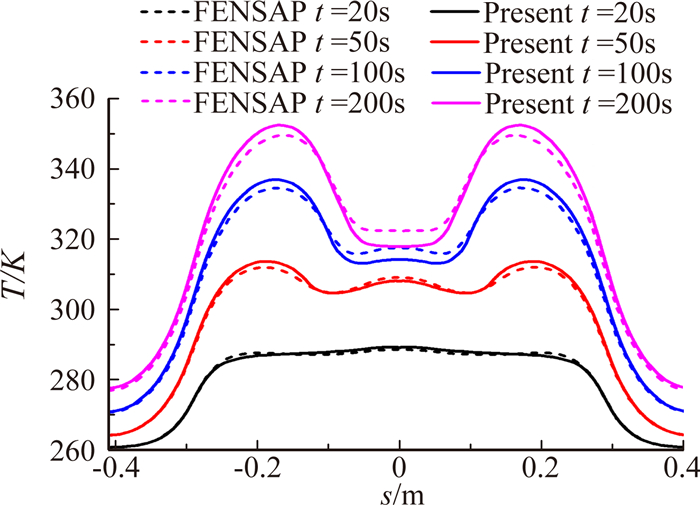
图 6是不同时间点帽罩表面温度分布情况。可以看出本文计算的表面温度分布趋势与FENSAP计算结果一致。在驻点附近,由于收集的水较多,防冰热载荷较大,其温度较低;往后推移,表面温度逐渐升高;防护区以外的表面温度最低。由于在计算热质平衡时,采用的方法不同,存在一定的误差。
|
| 图 6 帽罩表面温度分布 Fig. 6 Nose cone surface temperature distribution |
4 结果分析 4-1 电加热防冰启动特性
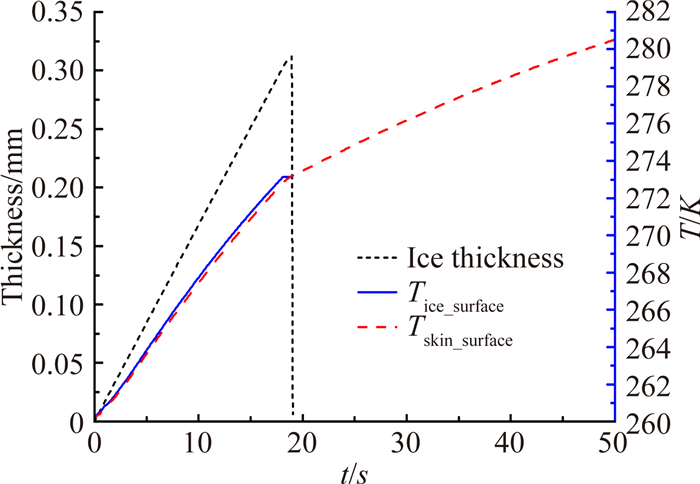
在电热防冰系统启动初期,旋转帽罩表面温度低于冰点温度,旋转帽罩表面会发生结冰,且当帽罩表面温度高于0℃时会发生冰脱落现象[24, 25, 26]。所以旋转帽罩电热防冰启动阶段是带有相变的复杂的传热传质过程。图 7为电加热防冰启动时,旋转帽罩驻点处的结冰厚度、冰层外表面温度及冰和蒙皮之间温度变化情况。
加热功率密度为1W/cm2,转速3000r/min,其他条件如环境温度、来流速度、来流压力、水滴直径、液态水含量等采用与第三节的相同数值。从图 7中可以看出,在前19s,驻点处表面温度在0℃以下,会发生结冰。在前18s,由于驻点冰表面温度较低,撞击到表面的水全部冻结,会结霜冰;当冰表面温度达到0℃时,收集的水部分冻结,结明冰,冰表面温度维持在冰点。但由于电加热器的加热作用,冰层底部和旋转帽罩表面温度很快达到0℃以上,发生冰脱落,帽罩表面进入无冰状态。
|
| 图 7 电热防冰启动过程 Fig. 7 Boot process of electro-thermal deicing |
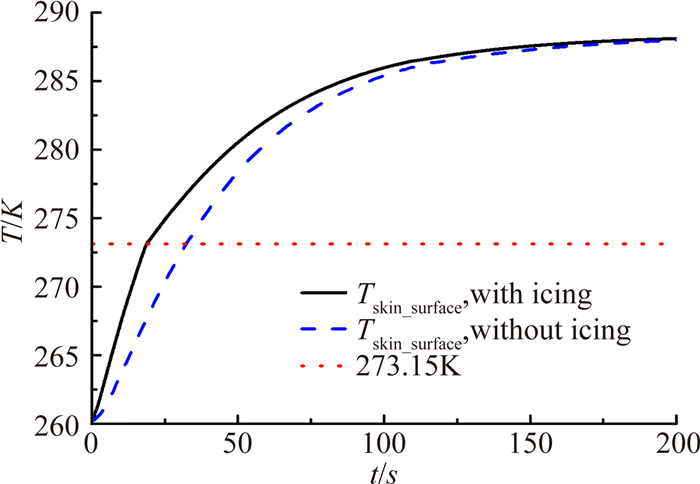
图 8为考虑结冰和不考虑结冰两种计算方法下,帽罩表面温度变化情况。可以明显看出当考虑帽罩表面结冰时,帽罩表面温度更快地达到0℃,这主要是由结冰潜热对帽罩加热引起的。这说明帽罩表面结冰加快了防冰系统的启动。但当时间足够长,帽罩表面温度达到稳定时,两种方法计算的稳定温度相同。这说明对于连续加热稳态防冰研究,可以不考虑结冰对旋转帽罩表面温度的影响,但对动态防冰进行研究时,则不能忽略。
|
| 图 8 两种电热防冰计算方法结果对比 Fig. 8 esults contrast of two calculation methods of electric heating anti-icing |
4.2 旋转对防冰表面温度的影响
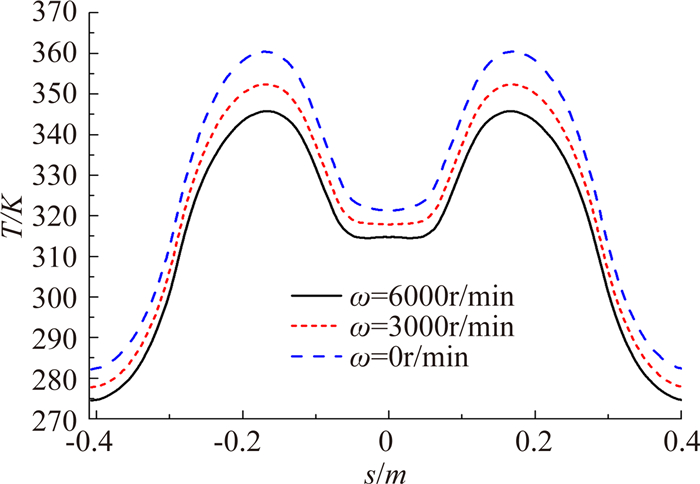
为了研究旋转对旋转帽罩电热防冰性能的影响,选取了三种转速进行计算,电加热功率密度为3W/cm2。由第3节可知,旋转转速越大,帽罩表面换热系数越大,这也就增大帽罩表面的防冰热载荷需求。图 9的结果也显示帽罩转速越大,在同等电加热防冰功率情况下,帽罩表面温度越低。
|
| 图 9 转速对防冰表面温度的影响 Fig. 9 nfluence of rotating speed on the anti-icing surface temperature |
4.3 两种加热方式的比较
与连续电加热防冰相比,一般认为周期性电加热除冰在节能和快速响应方面更有优势[27]。所谓周期性电加热除冰[28]是指除冰系统周期性地通电和断电进行除冰。电加热防冰同样可以使用周期性电加热。在通电加热时,帽罩表面温度会快速升高,而在断电时,表面温度会下降,但始终维持表面温度在0℃以上,从而实现防冰。
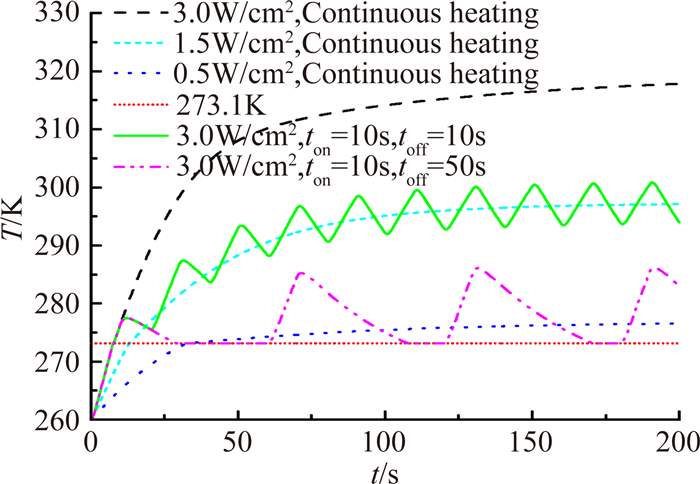
当加热器功率相同时,周期性电加热时,由于防冰系统并不是一直加热,在断电阶段并不消耗能量,所以周期性电热防冰具有节能效果。如图 10所示,在3W/cm2的加热功率下,驻点温度在周期电加热防冰情况下更低,不容易过热,在实现防冰功能的同时,耗能更少。
|
| 图 10 两种电加热方式的驻点温度对比 Fig. 10 Stagnation temperature contrast with two kinds of electric heating mode |
当能耗相同时(例如在图 10中,加热器功率3W/cm2,加热时间10s,断电时间10s时的防冰耗能与加热功率1.5W/cm2但连续加热时的防冰能耗是相同的)。启动防冰系统初期,周期电加热防冰的表面温度响应更快,能够更早地达到0℃以上。在后期,连续加热的表面温度会稳定在某一温度值,而周期性电加热的表面温度则会围绕这一温度值稳定波动。
由于周期电加热表面温度的谷值小于相同能耗下连续加热的稳定温度,所以其发生结冰的可能性更大。特别是在能耗较低时,如图 10所示,加热功率为0.5W/cm2,连续加热的表面稳定温度略大于0℃,能够实现防冰。加热器功率3W/cm2,加热时间10s,断电时间50s的能耗与之相同,但在断电冷却阶段,温度会降到0℃,发生结冰。由于其结的冰为明冰,故冰表面维持在0℃,帽罩驻点温度也维持在0℃左右,当加热再次启动时,驻点温度才开始上升,发生冰脱落。
通过以上分析可知,当电加热功率相同时,周期电加热防冰更为节能;当电加热能耗相同时,周期电加热系统启动响应更快,但相应增加了结冰的风险。
5 结 论旋转运动对帽罩表面对流换热起到增强作用,从而会导致防冰热载荷增加。旋转速度越大,帽罩防冰表面温度越低,所需要的防冰热载荷越大。
电热防冰启动阶段是复杂的传热传质过程,考虑表面结冰情况会缩短表面温度响应时间。在对动态防冰进行研究时,不能忽略结冰的影响。
当电加热功率相同时,周期电加热防冰更为节能;当电加热能耗相同时,周期电加热系统启动响应更快,结冰风险增加。
| [1] |
Qiu X G, Han F H.
Aircraft deicing system[M]. Beijing: Aviation Industry Press, 1985 : 196 -222.
(in Chinese) 裘燮纲, 韩风华. 飞机防冰系统[M]. 北京: 航空工业出版杜, 1985 : 196 -222. |
| [2] | Heinrich A, Ross R, Zumwalt G, et al. Aircraft icing handbook[R]. FAA Technical Center, 1991. |
| [3] |
Zhao Q Y, Dong W, Zhu J J. Water droplets collision characteristics of motor rotating rectifier cap analysis[J].Journal of Gas Turbine Test and Research, 2011, 24(4):32–35. (in Chinese) 赵秋月, 董威, 朱剑鋆. 发动机旋转整流帽罩的水滴撞击特性分析[J]. 燃气涡轮试验与研究, 2011, 24(4) : 32–35. |
| [4] |
Wu M L, Chang S N, Leng M Y, et al. Simulation of droplet impingement characteristics of spinner based on Eulerian method[J].Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(9):1263–1267. (in Chinese) 吴孟龙, 常士楠, 冷梦尧, 等. 基于欧拉法模拟旋转帽罩水滴撞击特性[J]. 北京航空航天大学学报, 2014, 40(9) : 1263–1267. |
| [5] |
Liu h, Guo W, Yang J, et al. The engine air intake cap anti-icing numerical simulation study of thermal load[J].Journal of Gas Turbine Test and Research, 2012, 25(1):44–48. (in Chinese) 刘华, 郭文, 杨军, 等. 发动机进气帽罩防冰热载荷的数值模拟研究[J]. 燃气涡轮试验与研究, 2012, 25(1) : 44–48. |
| [6] |
Wang J, Hu Y P, Ji H H, et al. Rotary fairing ice growth and loss in the process of the experiment[J].Journal of Aerospace Power, 2014, 29(6):1352–1357. (in Chinese) 王健, 胡娅萍, 吉洪湖, 等. 旋转整流罩积冰生长与脱落过程的实验[J]. 航空动力学报, 2014, 29(6) : 1352–1357. |
| [7] |
Hu Y P, Ji H H, Wang J, et al. The impact of cone angle on rotating fairing icing simulation[J].Journal of Aerospace Power, 2014, 29(3):495–503. (in Chinese) 胡娅萍, 吉洪湖, 王健, 等. 锥角对旋转整流罩积冰影响的模拟实验[J]. 航空动力学报, 2014, 29(3) : 495–503. |
| [8] |
Li X Y. Rotating parts freezing shrinkage than similarity experiment research[D]. Beijing: Beihang University, 2010. (in Chinese) 李西园. 旋转部件结冰缩比试验相似性研究[D]. 北京: 北京航空航天大学,2010. |
| [9] |
Wu M L. Rotating parts ice numerical simulation study[D]. Beijing: Beihang University, 2014. (in Chinese) 吴孟龙. 旋转部件结冰数值模拟研究[D]. 北京: 北京航空航天大学, 2014. |
| [10] | Dong W, Zhu J, Zheng M, et al. Thermal analysis and testing of nonrotating cone with hot-air anti-icing system[J].Journal of Propulsion and Power, 2015, 31(3):896–903. |
| [11] | Gilchrist S, Ewing D, Ching C Y. On the design of an aero-engine nose cone anti-icing system using a rotating heat pipe[J].Journal of Thermal Science and Engineering Applications, 2009(2):022002. |
| [12] | Axcell B P, Thianpong C. Convection to rotating disks with rough surfaces in the presence of an axial flow[J].Experimental Thermal and Fluid Science, 2001, 25(1):3–11. |
| [13] | KaysW M, CrawfordM E, WeigandB. Convective heat and mass transfer[M]. Tata McGraw-Hill Education, 2012 . |
| [14] |
Chang S N, Su X M, Qiu Y F. 3D wing icing simulation[J].Acta Aeronautica et Astronautica Sinica, 2011, 32(2):212–222. (in Chinese) 常士楠, 苏新明, 邱义芬. 三维机翼结冰模拟[J]. 航空学报, 2011, 32(2) : 212–222. |
| [15] | Dropkin D, Carmi A. Natural convection heat transfer from a horizontal cylinder rotating in air[J].Trans. ASME, 1957, 79(4):741–749. |
| [16] | Kays W M, Bjorklund I S. Heat transfer from a rotating cylinder with and without crossflow[J].Trans. ASME, 1958, 80(1):70–78. |
| [17] | Messinger B L. Equilibrium temperature of an unheated icing surface as a function of air speed[J].Journal of the Aeronautical Sciences, 2012, 20(1):29–34. |
| [18] |
Bu X Q, Lin G P, Peng Y X, et al. A new method to compute the deicing thermal load[J].Acta Aeronautica et Astronautica Sinica, 2006, 27(2):208–212. (in Chinese) 卜雪琴, 林贵平, 彭又新, 等. 防冰热载荷计算的一种新方法[J]. 航空学报, 2006, 27(2) : 208–212. |
| [19] |
Shi M H, Wang H, Hao Y L. Under the action of centrifugal force field research of forced convection heat transfer in porous media[J].Journal of Engineering Thermal Physics, 2002, 23(4):473–475. (in Chinese) 施明恒, 王海, 郝英立. 离心力场作用下多孔介质中强制对流换热的研究[J]. 工程热物理学报, 2002, 23(4) : 473–475. |
| [20] |
Guo Z Y. The physical mechanism of convective heat transfer and its control: synergy of velocity field and heat flow field[J].Chinese Science Bulletin, 2000, 45(19):2118–2122. (in Chinese) 过增元. 对流换热的物理机制及其控制: 速度场与热流场的协同[J]. 科学通报, 2000, 45(19) : 2118–2122. |
| [21] | Zeng Y G, Chao M Z. Thermal drive in centrifugal fields—mixed convection in a vertical rotating cylinder[J].International Journal of Heat and Mass Transfer, 1992, 35(7):1635–1644. |
| [22] |
Sheeran Del. Heat exchanger design handbook: Heat exchanger principle[M]. Mechanical Industry Publishing House, 1987. (in Chinese) 施林德尔,换热器设计手册: 换热器原理[M]. 机械工业出版社, 1987 |
| [23] |
Zhu J J, Dong W. Anti-icing parts surface flow heat transfer and temperature calculation analysis[J].Journal of Gas Turbine Test and Research, 2011(1):15–18. (in Chinese) 朱剑鋆, 董葳. 防冰部件表面流动换热与温度计算分析[J]. 燃气涡轮试验与研究, 2011(1) : 15–18. |
| [24] |
Chang S N, Yi S X, Huo X H, et al. To improve the electro-thermal deicing system simulation[J].Journal of Air Power, 2008, 23(10):1753–1758. (in Chinese) 常士楠, 艾素霄, 霍西恒, 等. 改进的电热除冰系统仿真[J]. 航空动力学报, 2008, 23(10) : 1753–1758. |
| [25] | Scavuzzo R J, Chu M L. Structural prosperities of impact ices accreted on aircraft structures[R]. NASA CR179580, 1987 |
| [26] | Scavuzzo R J, Chu M L, Ananthaswamy V. Influence of aerodynamic forces in ice shedding[J].Journal of Aircraft, 1994, 31(3):526–530. |
| [27] |
Xiao CH, Gui Y W, Du Y X, et al. Heat transfer characteristics of electro-thermal deicing icing wind tunnel experimental study[J].Journal of Experimental Fluid Mechanics, 2010, 24(04):21–24. (in Chinese) 肖春华, 桂业伟, 杜雁霞, 等. 电热除冰传热特性的结冰风洞实验研究[J]. 实验流体力学, 2010, 24(04) : 21–24. |
| [28] |
Chang S N, Hou Y Q, Yuan X G. Periodic electric heating control law of the deicing surface temperature[J].Journal of Air Power, 2007, 22(8):1247–1. (in Chinese) 常士楠, 候雅琴, 袁修干. 周期电加热控制律对除冰表面温度的影响[J]. 航空动力学报, 2007, 22(8) : 1247–1. |



