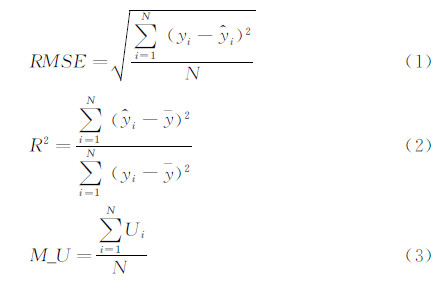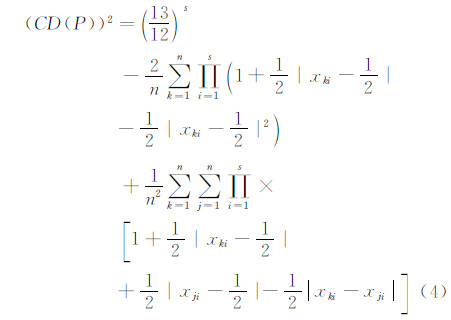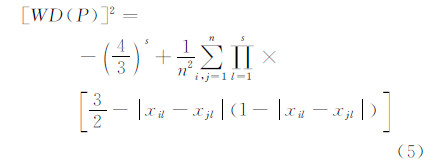0 引 言
现代风洞实验测试系统的构成越来越复杂,增加了实验中各环节的微弱变化所导致的系统误差来源,使得风洞实验误差的控制难度加大,同飞行器设计不断提高的数据质量要求之间的矛盾越来越突出。传统的单因子实验方法(OFAT方法)对实验环境变化导致的误差缺少控制和消除能力[1],且生产效率过低[2]。现代实验设计(MDOE)领域的研究表明通过改进实验设计,能够有效地减小甚至消除实验环境中不可控因素对实验结果的影响。风洞MDOE实验方法就是将现代实验设计理论应用于风洞实验产生的新技术,它能够用相对少量的实验次数,获得更高质量的数据。
MDOE方法通过建立统计模型来获取气动规律。统计模型有方差分析模型、参数回归模型、非参数回归模型和稳健回归模型等。形式实验设计方法是MDOE的重要组成,是对测量样本点数量和取值进行设计的方法。不同的统计模型需要不同的形式实验设计方法。方差模型适用于因素线性效应的研究,采用具有合适分辨力的部分因子设计[3],可以通过较全因子设计更少的实验次数,计算出主因素的效应和交互效应,并且有效避免主因素与交互作用及交互作用间出现混淆(Confounded)现象。参数回归模型能够给出气动力系数随姿态角、马赫数、控制面偏转角等自变量变化的非线性规律,在风洞MDOE中被广泛应用[4]。基于参数回归模型的MDOE的形式实验设计方法有中心复合设计(Center Composite Design,CCD)、面心复合设计(Face-centered Central Composite Design,FCD)和最优回归设计(Optimum Design)等[5, 6]。这些设计方法都属于回归设计,在进行设计前要确定气动模型的结构形式。
随着现代战斗机和导弹对机动性要求的不断提高,飞行器气动力规律通常是非线性和多变量耦合的,基于参数回归模型的MDOE方法已经不能满足要求。当气动规律的非线性较强时,基于多项式的响应面模型难以很好地对全局气动规律进行拟合[7, 8]。由于非参数模型较多项式模型有更强的非线性建模能力,所以基于非参数模型的MDOE方法逐渐被人们所关注[9]。非参数模型的形式实验设计一般采用拉丁超立方设计(Latin Hypercube Sampling,LHS)和均匀设计(Uniform Design),在风洞MDOE中还没有相关的研究。本文针对风洞非参数模型MDOE的形式实验设计方法开展研究,采用Kriging方法进行建模,对拉丁超立方设计和均匀设计应用于风洞实验的适用性进行比较,并根据风洞实验的特点发展相应的优化方法。
1 研究方法为了深入分析研究不同的实验设计方法的优缺点,本文通过建立标模实验气动模型,进行“虚拟”风洞实验。“虚拟”实验是实验设计方法研究中常用的方法,实验设计方法研究中需要频繁地对各种设计进行比较和优化,真实的风洞实验周期长、成本高,而虚拟风洞实验可以及时地获得结果,采用这种方法能够高效、低成本地进行实验设计方法的研究[10]。本文所采用的实验气动模型是利用在中国航天十一院FD-06风洞已有的大量标模实验数据构建的。输入一组新的设计样本点,就可以获得该样本对应的六分量气动数据和不确定度,完成一次“虚拟”的风洞实验过程。然后根据虚拟风洞实验结果,进行建模和数据分析,通过和实验气动模型(即标准响应面)相比较,考核其还原气动模型的能力。
自变量的设计空间如下:
迎角:0°~40°;
滚转角:0°~90°。
响应变量:法向力系数CN,前体轴向力系数CAF,侧向力系数CZ,俯仰力矩系数mzg,偏航力矩系数myg和滚转力矩系数mx。
检验设计优劣除了通过数据和绘图直接对比外,还利用统计方法对各种设计方法建立的响应面模型的近似精度进行比较。选择一定量均布于设计空间的检验点,分别代入标准响应面和样本点建立的响应面模型得到标准值yi、预测值y^i和预测值的不确定度Ui,采用整体均方根误差RMSE和判定系数R2对新响应面模型的拟合程度进行评估,采用整体平均不确定度M_U对预测误差进行评估,公式分别如下:
其中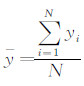 ,N为检验点个数。RMSE越小,R2越接近1,模型还原程度越高。M_U越小,实验误差越小。
2 MDOE风洞实验设计方法的选择
,N为检验点个数。RMSE越小,R2越接近1,模型还原程度越高。M_U越小,实验误差越小。
2 MDOE风洞实验设计方法的选择
拉丁超立方设计和均匀设计,二者也被称为是“空间填充设计”[11]或者“空间抽样设计”[12]。“没有最好的设计,只有最适合的设计”[13],本文根据风洞实验的特点,对这两种方法的适用性进行研究。
2.1 拉丁超立方设计拉丁超立方法是应用广泛的现代实验设计技术之一,取样覆盖均匀,适用于影响因素较多的情况,可显著减少实验规模[14],实验次数等于水平数。拉丁超立方抽样是按如下方法选取设计点的:
设有n个设计变量,每个变量p个水平,拉丁超立方抽样将每个设计变量分为p个区间,因均匀分布,p个区间等间隔。这样整个变量空间分成pn个了区域。遵循下列两个原则取实验点:
1)样本点在每个了区域随机选取;
2)在任一维,即任一变量上的投影有p个区间,每个区间有且仅有一个样本点。
由于拉丁超立方设计是一种随机抽样设计方法,容易产生分布不均匀的较差设计,所以通常加以一定的准则以保证其均匀性,常用的准则有最大最小距离(Maximize minimum distance)、最小最大距离(Minimize maximum distance)、最小差异准则(Minimize discrepancy)、相对理想累积分布最小均方根差异准则(Minimize RMS variation from CDF)和相对理想累积分布最小最大差异准则(Minimize maximum variation from CDF)。本文对以上几种准则条件下的LHS设计进行对比。设计样本点为40个,通过“虚拟”风洞实验获得样本数据,然后用样本数据建立样本点响应面和标准响应面进行比较。
对于模型的6个气动力和力矩分量,需要建立6个响应面。通常纵向气动系数的响应面模型非线性程度要比横向的弱,如果样本点能够满足横向气动系数响应面模型的建立,纵向也能够满足。图 1~图 5给出了基于上述5种不同准则下的LHS样本设计及其建立的滚转力矩系数mx响应面。表 1给出了检验点的统计分析结果。
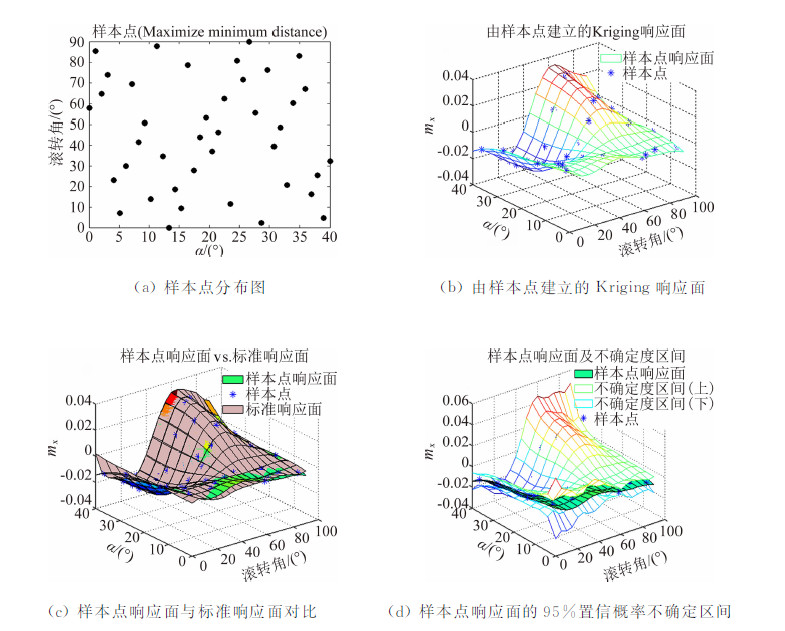 |
| 图 1 LHS样本点及响应面(最大最小距离准则)Fig. 1 Sample points of LHS design and the response surface (Maximize minimum distance) |
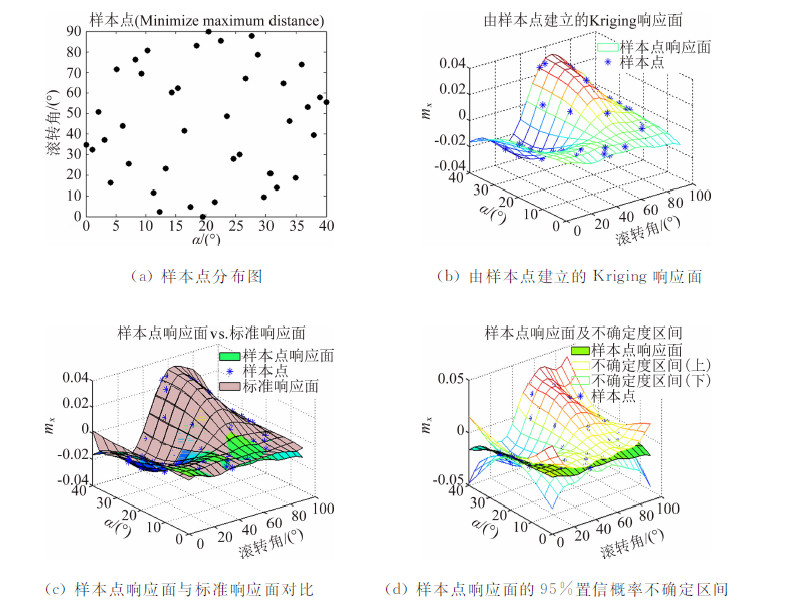 |
| 图 2 LHS样本点及响应面(最小最大距离准则)Fig. 2 Sample points of LHS design and the response surface (Minimize maximum distance) |
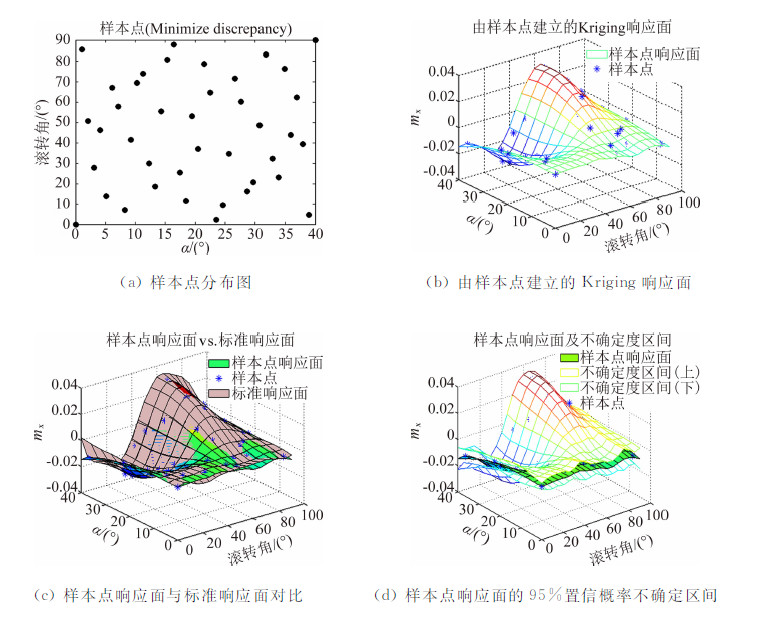 |
| 图 3 LHS样本点及响应面(最小差异准则)Fig. 3 Sample points of LHS design and the response surface (Minimize discrepancy) |
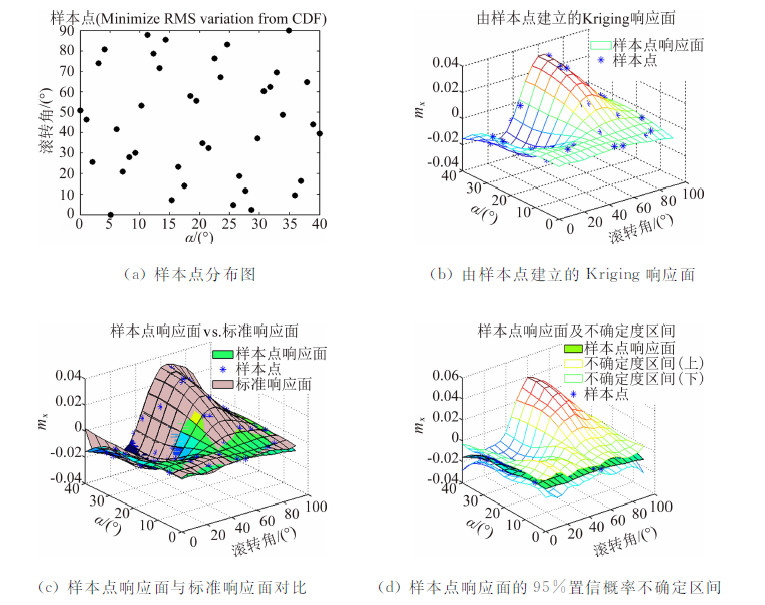 |
| 图 4 LHS样本点及响应面(相对理想累积分布最小均方根差异准则)Fig. 4 Sample points of LHS design and the response surface (Minimize RMS variation from CDF) |
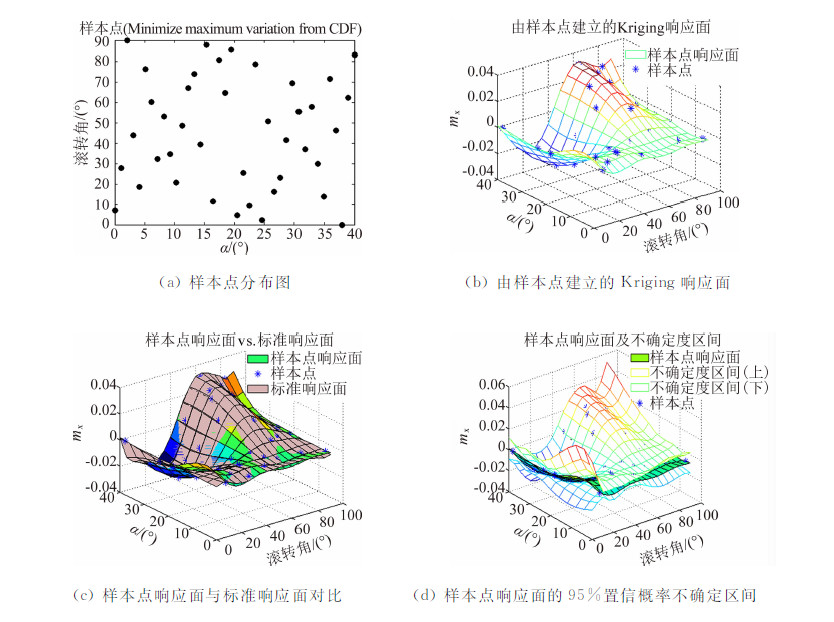 |
| 图 5 LHS样本点及响应面(相对理想累积分布最小最大差异准则)Fig. 5 Sample points of LHS design and the response surface (Minimize maximum variation from CDF) |
| 不同LHS设计 | 样本点个数 | 检验点个数 | RMSE | R2 | M_U |
| 最大最小距离准则 | 40 | 3731 | 0.0013 | 0.9924 | 0.0048 |
| 最小最大距离准则 | 40 | 3731 | 0.0015 | 0.9930 | 0.0040 |
| 最小差异准则 | 40 | 3731 | 0.0017 | 0.9575 | 0.0035 |
| 相对理想累积分布最小均方根差异 | 40 | 3731 | 0.0020 | 0.9396 | 0.0069 |
| 相对理想累积分布最小最大差异 | 40 | 3731 | 0.0021 | 0.9892 | 0.0047 |
从检验参数看,不同准则下的LHS设计的整体模型精度均较高,差异不明显。从样本点响应面与标准响应面对比图可以看出,如果在某局部区域缺少样本点,就容易出现局部预测误差较大的问题,如滚转角0°、迎角接近40°附近,预测响应面的mx普遍偏大,而标准响应面的mx在此处为小量。只有采用了相对理想累积分布最小最大差异准则的LHS样本点的响应面(图 5),其原因是该设计在此位置有一个样本点。
所以,LHS设计尽管已经采用了一些促进其“均匀化”的准则,但仍然容易出现某个局部没有样本点的情况,这会导致较大的预测偏差和不确定度,是风洞实验难以接受的。其次,LHS的样本点生成有随机性,带来两个问题:一是每次设计的质量会有差异,稳定性不高;二是每次设计中样本点分布不佳的区域和程度不同,不便于进行优化。
2.2 均匀设计均匀设计[15]由我国方开泰和王元院士提出,是一种空间填充(Space Filling)设计。均匀设计要求实验点均匀的分布在实验区域内,均匀设计基于偏差来衡量样本点在设计空间分布的均匀性,使得设计空间内各区域能够均等的“获得”样本点信息,每个样本点所承载的信息也能够在建模中被充分利用,这一优点非常适合MDOE风洞实验设计。
均匀性准则要求设计具有最好的均匀性,对于一个设计,若没有其他设计比它有更小的偏差,则称该设计为均匀设计[16]。为了衡量设计的均匀性,人们提出了偏差这个概念来衡量实验点集在实验区域内散布均匀程度。不失一般性,假设实验域为Cs=[0, 1]s。记P={x1,…,xn}=(xij)n×s为Cs上的一个有n个实验点的设计,它可表为n×s的矩阵,其中n表示实验点数,s表示因子的个数。Hickernell[17]用泛函分析中再生核Hilbert空间的方法将古典的诸偏差表成统一形式,并且定义了许多新偏差,其中应用得最广泛的是如下的中心化L2-偏差CD(P):
和可卷型L2-偏差WD(P):进行样本点数量为40个的均匀设计,图 6(a) 给出了一个设计结果,表 2给出了样本点的偏差计算和响应面检验结果。均匀设计的样本分布整体上非常均匀,没有较明显的“团聚”和“缺失”区域,所建立的响应面检验结果也优于LHS设计结果。从图 6(c) 和6 (d)可以看出,除了设计空间的边缘位置外,样本点响应面和标准响应面吻合良好,没有差异或不确定度特别大的局部区域。
| 中心化偏差CD | L2-偏差D | 修正偏差MD | 对称化偏差SD | 可卷偏差WD |
| 0.014 3 | 0.011 2 | 0.015 2 | 0.045 | 0.022 3 |
| 样本点个数 | 检验点个数 | RMSE | R2 | M_U |
| 40 | 3 731 | 0.001 4 | 0.999 | 0.001 8 |
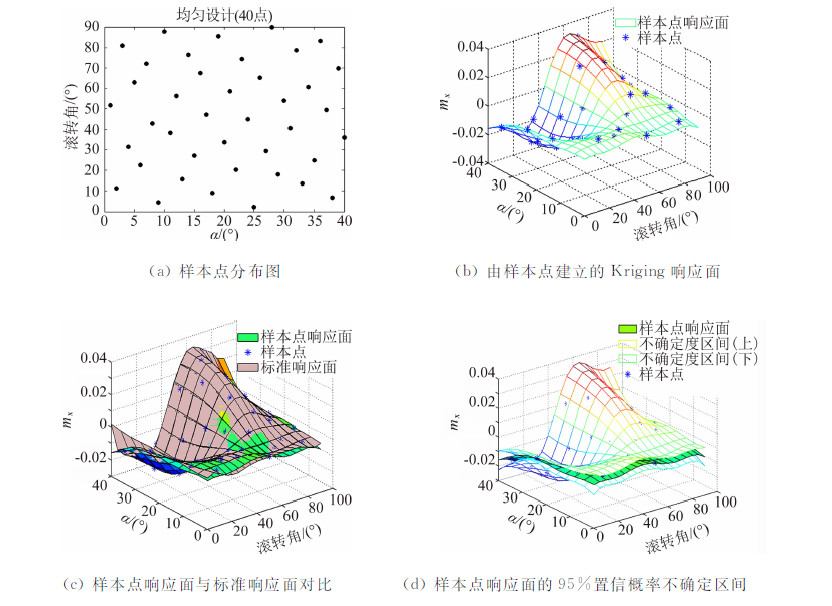 |
| 图 6 均匀设计样本点及响应面Fig. 6 Sample points of Uniform Design and the response surface |
所以,对于风洞实验均匀设计较LHS更为稳健、均匀,更适合在MDOE风洞实验中应用。
3 均匀设计应用于MDOE风洞实验的优化与改进均匀设计得到初始实验设计结果还无法满足风洞实验的要求,还要根据风洞实验的具体特点加以优化。本文发展了几种对均匀设计的优化改进方法,可以进一步提高样本点设计质量,使其满足风洞实验的要求。
3.1 边界点补充对于飞行器气动模型,边界位置的数据质量往往是非常重要的,而且当飞行器处于最大姿态角位置时,气动规律出现非线性的可能性增大,要求数据尽可能内插,以防止外插带来的风险。边界点的增加包括角点和边线点,补充边界点后的设计如图 7所示。补充边界点时先将设计空间进行了标准化,即将各自变量范围转换到[0,1]区域内,补充方法如下:
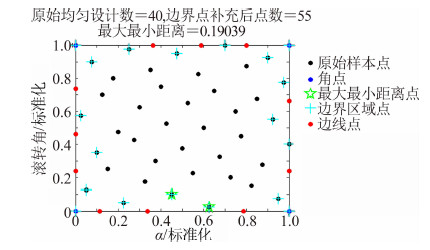 |
| 图 7 均匀设计边界点补充示意图Fig. 7 Boundary points filling of Uniform Design |
1)角点直接在设计空间角点增加,即[0,0],[0,1],[1,0],[1,1];
2)计算原始设计样本间的最大最小距离Dmaxmin,即每个样本点和其他点的最小距离中的最大值,本例中Dmaxmin为0.190 39,出现Dmaxmin的两个点在图 7中用“☆”标记;
3)确定边界影响区域范围,这是给边界提供建模信息的区域,通过判断该区域点的分布来决定边线点增加的位置。如本例取0.1作为划分界限,距离四个边界为0.1的点视为边界影响区域样本点,在图 7中用“+”标出。
4)对边界影响区域样本点在其边界方向的距离进行判断,如果距离大于Dmaxmin,则在边界以等分方式增加样本点,直至边界影响区域样本点在其边界方向的距离都小于Dmaxmin,结果如图 7所示。
3.2 样本点密度调整为了提高实验数据的精确度,风洞实验中常常在会发生气动规律剧烈变化的自变量区域,或者研究者特别关注的实验状态附近,减小实验点间隔,增加样本点。均匀设计的样本点在设计空间内“均匀散布”,适合于研究中各区域的信息密度需求相同的情况。当有先验信息时,在其基础上改变样本点分布密度,更符合风洞实验的实际。图 8给出了迎角方向改变密度分布前后的对比,对于迎角0°~12°范围的样本点,迎角方向间隔增加到1.2倍,多出的点移入12°~40°的区间;迎角12°~40°范围的样本点,迎角方向间隔减小为原来的0.914 3倍。由于迎角大于12°后气动规律随迎角变化更为强烈,改变密度分布后迎角12°到40°的区间样本点增加了2个,提高了大迎角区域的样本点密度,更为合理。
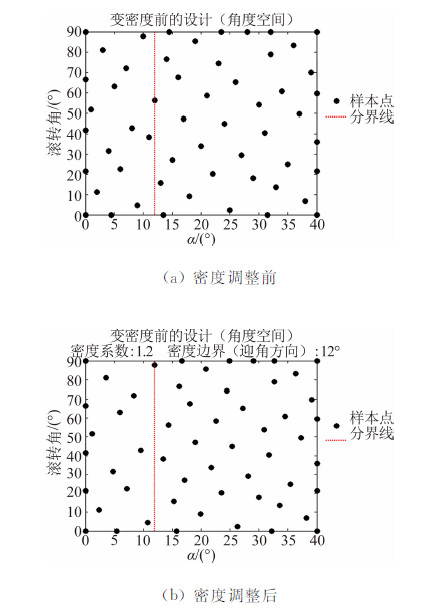 |
| 图 8 样本点密度调整前后对比Fig. 8 Comparison the distributions of pre-and-after adjusting of the density of sample points |
重复点数量由实验的不确定度目标和实验环境所决定,实验环境误差大,要获得高质量水平的数据,重复的次数需要多些。重复点的设计可以根据先验来决定,如在规律变化剧烈或评价检测风洞系统稳定性的某些关键位置。除此之外,角点和边线点位置也是设置重复点的重点区域。对设计空间的内部点,重复点设置可以随机选择,也可以按照均匀设计方法进行选择,图 9给出内点重复设计的结果。
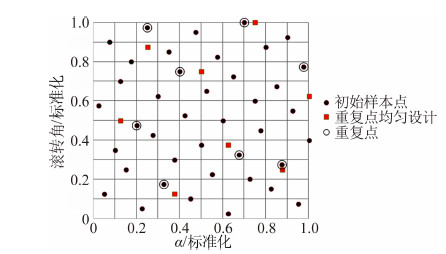 |
| 图 9 设计空间内重复点的设计Fig. 9 Design of the repetitive points in the design space |
本节将均匀设计及其优化方法应用于基于Kriging模型MDOE实验,设计变量为迎角和滚转角。
4.1 实验条件风洞模型为导弹类标模,外形为舵身组合体,四片尾舵在0°滚转角时呈“X”字布局。实验马赫数为1.79,自变量的设计空间为:迎角0°~40°;滚转角0°~90°。
OFAT实验的实验测量点如图 10所示,共有108个测量点。表 3给出了对六分量测力数据的实验数据不确定度。
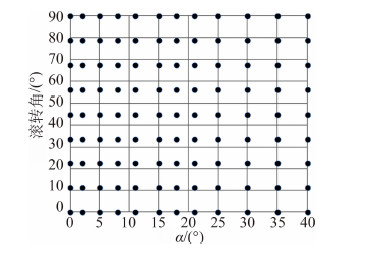 |
| 图 10 OFAT实验的实验测量点分布Fig. 10 Distribution of the sample points in OFAT test |
| UCN | UCAF | UCZ |
| 0.08 | 0.012 | 0.04 |
| Umzg | Umyg | Umx |
| 0.014 | 0.032 | 0.002 |
初始样本点为35点的均匀设计,增补了边界点和重复点后最终设计为72个。样本点组成为:初始均匀设计35个;角点4个;边线点9个;重复点24个。
MDOE方法测量点要比OFAT方法的少36个点,测量点为OFAT方法的66.7%。为了增加大迎角下的测试点密度,迎角0°~12°范围的样本点在迎角方向间隔增加到1.2倍,最终设计如图 11所示。
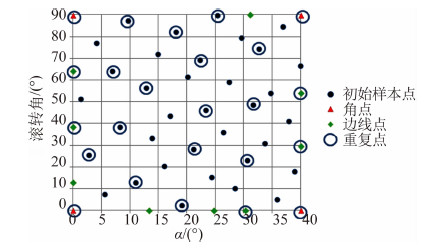 |
| 图 11 MDOE方法最终样本点设计Fig. 11 Final design of the sample points in MDOE test |
通过“虚拟”风洞实验获得72个样本点的六分量气动力和力矩系数后对其进行建模,获得图 12所示的响应面模型和不确定度评估。可以看出,利用均匀设计为基础进行优化所得到的样本点设计,拟合出的气动响应面规律合理。尽管该模型的横向气动力和力矩系数表现出随自变量强烈的非线性变化规律,样本点对其非线性特征的采样非常充分和准确。通过非参数建模的方式,能够以非常直观的形式表示出气动特性随迎角和滚转角变化的规律,有利于分析和研究;而且以响应面模型给出风洞实验结果,任意自变量组合的值都可以直接获得,具有信息量大的优点。图 12右侧一列给出了MDOE结果的不确定度,满足实验要求。
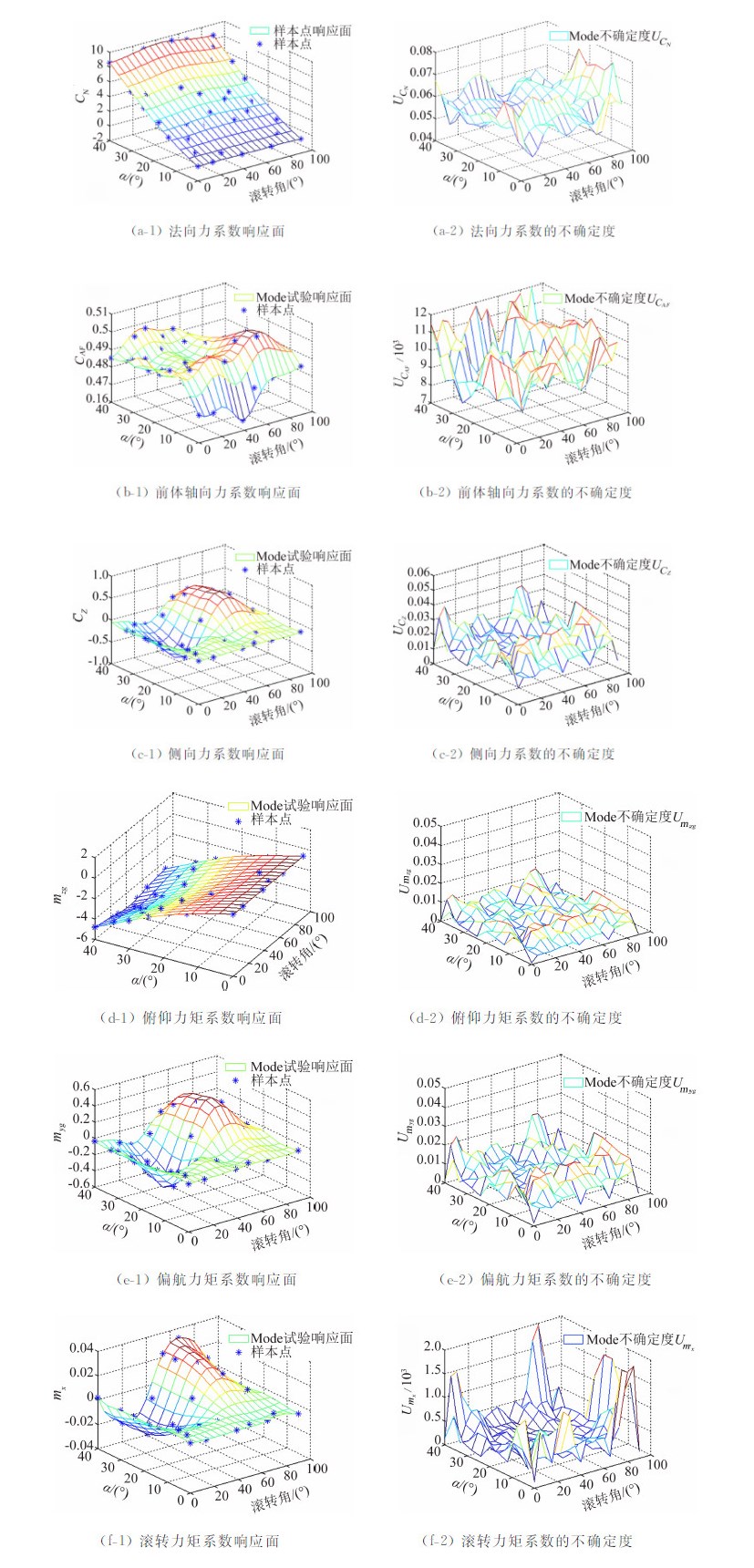 |
| 图 12 MDOE方法的六分量气动力和力矩系数的响应面及不确定度Fig. 12 Response surfaces and uncertainty of aerodynamic parameters in MDOE test |
本文对风洞非参数模型MDOE的形式实验设计方法进行了研究,对拉丁超立方设计和均匀设计应用于风洞实验的适用性进行比较,并根据风洞实验的特点发展几种优化方法,主要结论有:
(1)对于风洞实验均匀设计较拉丁超立方设计更为稳健、均匀,更适合基于非参数模型的风洞MDOE方法。
(2)在均匀设计方法基础上,根据风洞实验的特点发展了优化的方法,包括边界点补充、样本点密度调整和重复点设计,能够将已有的“先验信息”应用于实验设计中。
(3)利用均匀设计为基础进行优化所得到的样本点设计,所需的测量点要少于OFAT方法的(如示例中所用的测量点数仅为OFAT方法的66.7%),且能够充分和准确地对较剧烈的非线性变化规律进行采样。
| [1] | DeLoach R. Applications of modern experiment design to wind tunnel testing at NASA Langley research center[R]. AIAA 98-0713, 36th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, Jan. 1998. |
| [2] | DeLoach R, Micol J R. Comparison of resource requirements for a wind tunnel test designed with conventional vs. modern design of experiments methods[R]. AIAA 2011-1260, 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, Florida, January 4-7, 2011. |
| [3] | Box G E, Hunter W G, Hunter J S. Statistics for experimenters:an introduction to design, data analysis and model building[M]. 1978. |
| [4] | Drew Landman, Jim Simpson, Dan Vicroy, et al. Efficient methods for complex aircraft configuration aerodynamic characterization using response surface methodologies[J]. Journal of Aircraft, 2007, 44(4):1189-1195. |
| [5] | 何为, 薛卫东, 唐斌. 优化实验设计方法及数据分析[M]. 北京:化学工业出版社, 2012. |
| [6] | Box G E, Hunter W G, Hunter J S. Statistics for experimenters:an introduction to design, data analysis and model building[M]. 1978. |
| [7] | Richard DeLoach, Erickson Gary. Low-order response surface modeling of wind tunnel data over truncated inference subspaces[R]. AIAA 2003-0456, 2003. |
| [8] | Erickson G E. Estimation of supersonic stage separation aerodynamics of winged-body launch vehicles using response surface methods[R]. NASA/TM-2010-216196, 2010. |
| [9] | Ching F Lo, Zhao J L, DeLoach R. Application of neural networks to wind tunnel data response surface methods[R]. AIAA 2000-2639, 2000. |
| [10] | DeLoach R, Micol J R. Comparison of resource requirements for a wind tunnel test designed with conventional vs. modern design of experiments methods[R]. AIAA 2011-1260, 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, Florida, January 4-7, 2011. |
| [11] | Kai-Tai Fang, Runze Li, Agus Sudjianto. Design and modeling for computer experiments[M]. London:Taylor & Francis Group,LLC. |
| [12] | 王劲峰, 姜成晟, 李连发. 空间抽样与统计判断[M]. 北京:科学出版社, 2009. |
| [13] | 方开泰. 实验设计与建模[M]. 北京:高等教育出版社, 2001. |
| [14] | 游海龙, 贾新章, 张小波, 等. Kriging插值与拉丁超立方实验相结合构造电路元模型[J]. 系统仿真学报, 2005, 17(11):2752-2755. |
| [15] | 方开泰. 均匀设计与均匀设计表[M]. 北京:科学出版社, 1994. |
| [16] | Fang K T, Wang Y. Number-theoretic methods in statistics[M]. Chaprrzanand Hall, London, 1994. |
| [17] | Hickernell F J. A generalized discrepancy and quadrature error bound[J]. Mathematics of Computation, 1998, 67:299-332. |