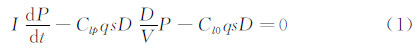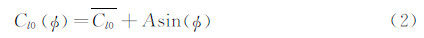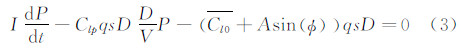0 引 言
战略导弹在再入大气层的过程中,由于烧蚀的作用,弹头表面会产生外形的小不对称,因此将产生小滚转力矩。该小滚转力矩无论起加速或减速弹头滚转运动的作用,都会带来滚转共振、滚转过零等一系列滚转异常问题,将直接影响弹头的战术技术性能[1, 2]。
对于再入弹头烧蚀产生小滚转气动力问题的研究国内外均有一定进展[1, 2, 3, 4, 5, 6],研究内容涵盖了烧蚀量的产生和确认、烧蚀产生小滚转力矩系数的测量等。其中中国空气动力研究与发展中心的赵忠良等[3]采用气浮轴承与固定天平相结合的方式，实现了固定姿态模型的小滚转静力矩系数测量；中国航天空气动力技术研究院的白葵等[6]利用基于气浮轴承的自由滚转试验方法，实现了小滚转气动力的测量，试验结果测量的滚转静力矩系数精度达到10-6量级，且能够同时测得滚转阻尼力矩系数。在这些研究当中，固定姿态模型试验测得的滚转静力矩系数是当次试验姿态的瞬时量；自由滚转试验获得的滚转静力矩系数是整个滚转过程中的平均量。而在实际的飞行当中，再入弹头作持续的滚转运动，是一个动态的过程，若弹头为惯性弹头，外形轴对称，滚转静力矩系数不随滚转角变化，其瞬时量和平均量基本能够满足工程使用需求；但随着对再入战略武器有效突防要求的不断提高，国内外逐渐由传统的惯性再入武器向机动式再入武器发展，基于传统轴对称布局的惯性再入弹头，也通过安装控制翼[7]、底部削平[8]等造成基本外形不对称的方式来增强机动能力，这就使得弹头在带迎角滚转的过程中，滚转静力矩系数随滚转角的周期性变化而变化。同理，烧蚀造成的小不对称在迎角不为零的情况下，所产生滚转静力矩系数在不同滚转角位置也不一样。综上所述，滚转静力矩系数的瞬时量和平均量不足以满足再入机动武器的发展需求，因此，风洞试验对烧蚀产生的小滚转气动力进行更为精细、准确测量显得尤为重要。
本文针对再入弹头发展趋势及其小滚转气动力测量需求，基于气浮轴承的自由滚转式小滚转力矩测量系统，采用多孔光栅及高灵敏度光电传感器测量带小突起(如边条、小配平翼)的非轴对称试验模型自由滚转状态下的角速度变化过程。同时根据试验对象布局特征建立相应滚转力矩气动力模型进行了理论验证，使用传统的试验数据处理方法结合飞行动力学仿真计算，获得了试验模型在滚转运动中的滚转气动力随时间的变化曲线，以及任意滚转角位置的小滚转静力矩系数。
1 试验设备及模型 1.1 测量系统机动式再入弹头小滚转气动力测量系统的硬件设备主要包括气浮轴承、多孔光栅和光电传感器、支杆、供气管路、控制柜和采集计算机，如图 1所示。其中，气浮轴承是测量系统的核心设备，主要包括转子、定子、模型支撑架以及正反向驱动涡轮(图 2)。转子与定子之间缝隙约为0.05mm，且定子的周向及前后端都安装了节流器，可以对轴承进行起浮和前后向止推。同时，后端安装了可以进行正、反向气流驱动的涡轮机构，能够更为方便的对模型转速进行控制。气浮轴承加载试验表明，当轴承供气压力为0.7MPa时，径向及轴向承载能力为50kg，以轴承中心为参考点的力矩承载能力为50N·m。由于自由滚转试验模型尺寸较大，该参数指标能够满足小迎角范围内的风洞试验。
 |
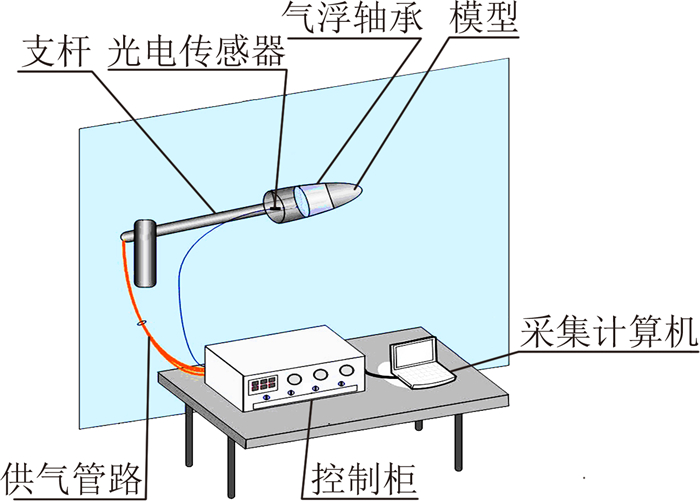| 图 1 小滚转气动力测量系统Fig. 1 Micro-rolling-moment measurement system |
 |
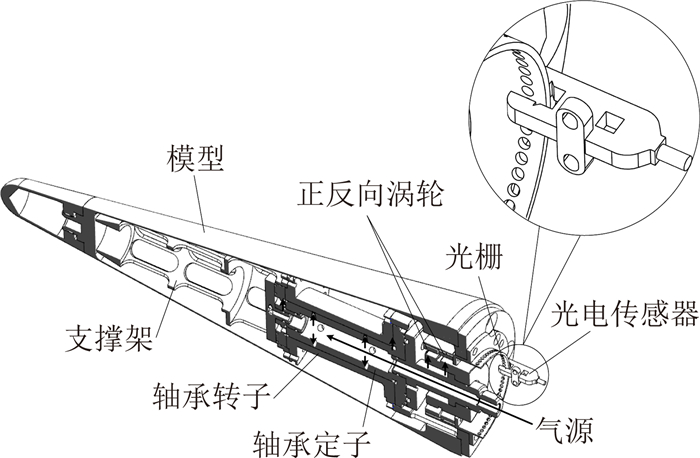| 图 2 气浮轴承及模型装配Fig. 2 Gas bearing and test model assembling |
测量系统中，控制柜内部包含气源过滤器、调压阀、供气开关、数据采集卡、智能控制仪等。中压气源进入控制柜后，气流经过过滤、调压后，分三路分别通往气浮轴承、正向驱动涡轮、反向驱动涡轮，可分别通过相应气路开关控制轴承的起浮及正、反向旋转驱动控制，以达到试验所需转速。如图 2和图 3所示，在模型旋转的过程中，安装于模型尾部的多孔光栅跟随模型旋转，而固定于支杆上的光电传感器保持不动。因此当光栅上的孔通过光电传感器时，传感器的状态为开，输出高电压信号(约8 500mV)，反之传感器状态为闭，输出低电压信号(约5 700mV)。随着模型和光栅的不断旋转，光电传感器不断开/闭生成高/低电压信号(图 4)。根据信号采集频率、光栅孔间隔角度等系统信息，可通过高/低电压信号计算获得模型转动角速度和角加速度随时间的变化，如图 4，显示了某试验车次0.4s内光电传感器的原始电压信号和相应的模型角速度变化曲线。本文中，试验测量系统的数据采集频率为25kHz，多孔光栅周向平均分布72个光栅孔，每孔间隔角度为5°。
 |
| 图 3 多孔光栅和光电传感器Fig. 3 Photo of grating and photoelectric sensor |
 |
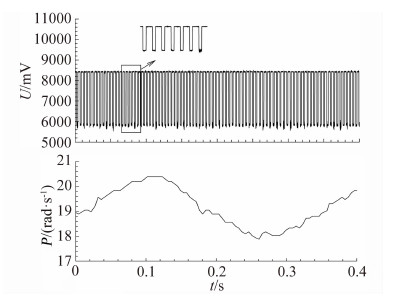| 图 4 原始电压信号和相应的模型角速度变化曲线Fig. 4 Original voltage signals and time courses of rolling rate |
为测量非对称外形和烧蚀等造成的小滚转气动力，采用了在轴对称光弹模型的基础上，添加配平翼和用边条模拟烧蚀的非轴对称模型进行试验，图 5显示了不同模型的示意图。
 |
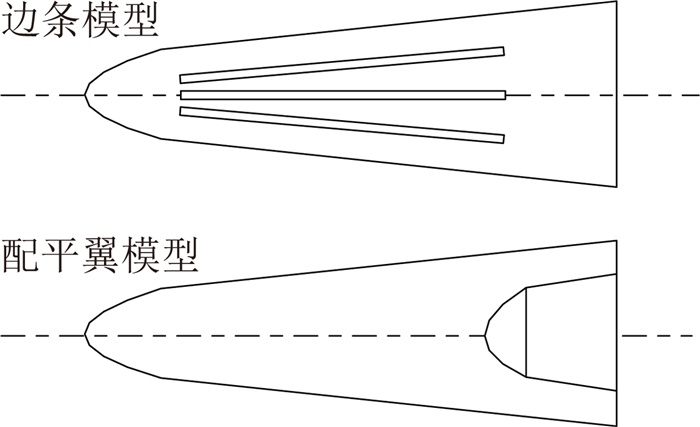| 图 5 模型示意图Fig. 5 Sketch of models |
要获得滚转阻尼力矩系数和滚转静力矩系数，还需要模型的外形参数和滚转转动惯量等信息。不同模型滚转转动惯量由附加质量法获得[2]，模型底部直径为140mm，边条规格0.7mm×3.5mm×3(厚度×宽度×条数)，每条周向角间隔22.5°。
2 试验原理及方法 2.1 控制方程
风洞启动后，模型在风洞中作自由滚转运动，可用滚转运动方程进行描述：
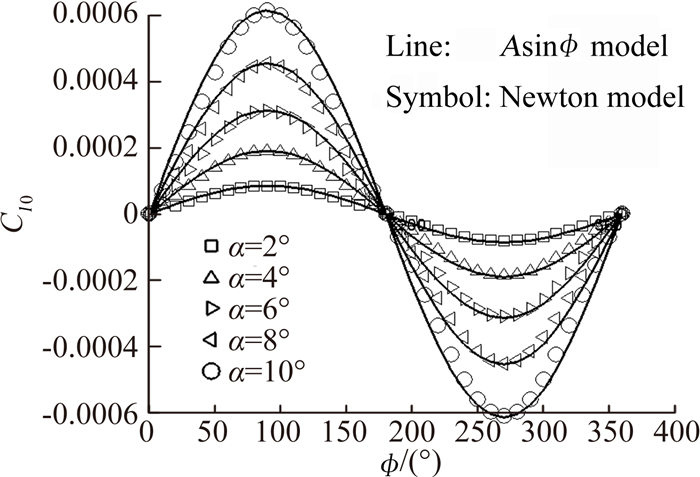
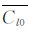为平均滚转静力矩系数，A为Cl0变化振幅，Φ为模型滚转角，取Φ=0时Cl0= 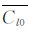。为验证此滚转静力矩模型的合理性，选取图 5所示配平翼布局为例，建立三维外形并使用三角面元网格进行表面离散，采用牛顿法[9]对风洞试验状态进行工程估算，获得不同迎角下滚转静力矩系数随滚转角变化曲线，如图 6所示。由图可见，将三角函数对滚转静力矩的变化进行描述是合理的。将式(2)带入式(1)，滚转运动控制方程变为：
 |
| 图 6 滚转静力矩气动模型验证Fig. 6 Model validation of rolling moment |
因此，在已知模型外形参数、转动惯量和风洞气流参数的条件下，可基于模型转速的变化数据，根据控制方程式(3)对试验数据进行处理，从而得到滚转阻尼系数Clp、平均滚转静力矩系数 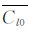、以及滚转静力矩系数的变化幅度A等气动力系数。若迎角为零，Cl0不随Φ角变化，即A为零，式(3)与式(1)等同，因此式(1)可视为式(3)的平均简化。
如前文所述，为实现精细化测量，测量设备和控制方程考虑了滚转静力矩随滚转角的变化，滚转运动方程更复杂化，需要计算的气动力系数较多。因此试验数据的处理采用最小二乘法结合动力学仿真计算，打靶法匹配试验结果曲线的方法。试验数据处理流程简图如图 7所示，其主要步骤如下：
 |
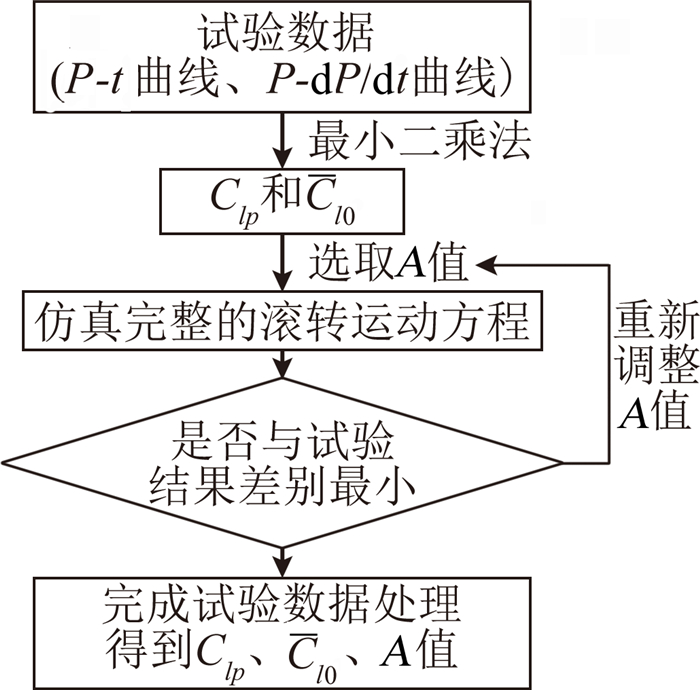| 图 7 试验数据处理流程简图Fig. 7 The flow chart of data processing |
1) 基于式(1)所示的简化控制方程使用最小二乘法对模型转速、转加速度变化曲线(P~dP/dt曲线)进行最小二乘拟合，可获得滚转阻尼系数Clp和平均滚转静力矩系数 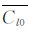。此方法与文献[2]、[6]中方法类似，这里不再赘述。以往的自由滚转试验都是按照此步方法进行数据处理，所得滚转静力矩系数均为平均量[6]。
2) 在获得Clp和 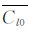的基础上，不断调整A的值，采用改进欧拉法对完整的滚转运动方程(式(3))进行仿真模拟，寻找最适合的A的值，使得仿真结果与试验结果差别最小，从而确定滚转静力矩系数Cl0随滚转角的正弦变化规律。
在匹配仿真结果与试验结果，寻找合适A值的过程中，本文采用打靶法[10]来寻找该值。打靶法的主要思路是适当选择和调整初值条件，求解初值问题使之逼近给定条件(仿真结果与试验结果差别最小)，此不断调整初值条件的求解过程类似于不断调整试射条件使之达到预定靶位，故称之为打靶法。同时，引入欧几里德距离[11]或TIC系数[12]最小作为匹配的条件判据，试验数据处理结果显示，两种条件判据所得结果一致。
3 试验结果与分析通过前文的讨论可知，进行试验数据处理，除试验模型的参数外，还需要给出气流参数。本文试验中，试验马赫数Ma=5.0，试验迎角α=0、2°、4°、6°，侧滑角β=0°，总压p0=1×106Pa，总温T0=353K，来流动压q=36 000Pa，来流速度V=76 000m/s。试验中，模型角速度变化范围约为600r/min~150r/min。
为与以前的试验结果[6]进行比较，验证试验技术的可靠性，首先使用了1.2°翼偏角标准模型进行试验。如表 1所示，标模试验的结果与之前试验结果一致，试验设备和测量系统可靠。同时，地面试验结果表明滚转静力矩系数的测量精度达到10-7量级，满足试验的测量要求。
本文试验中，由于模型的滚转阻尼系数和滚转静力矩系数都较小，模型转速下降较慢，因此同一试验状态需要分2~3次试验才能完成整个转速变化范围的测量，各个转速段的试验数据处理结果进行平均处理，可获得最终各个迎角下，不同模型安装状态的平均滚转力矩和滚转阻尼力矩系数。图 8给出了边条外形、α=0°试验状态时，不同试验车次的平均转速变化曲线。图 8的结果显示，同一试验状态不同试验车次高、低转速测量结果连续性、转速重叠区域重复性都较好，也直接验证了试验系统的可靠性。
 |
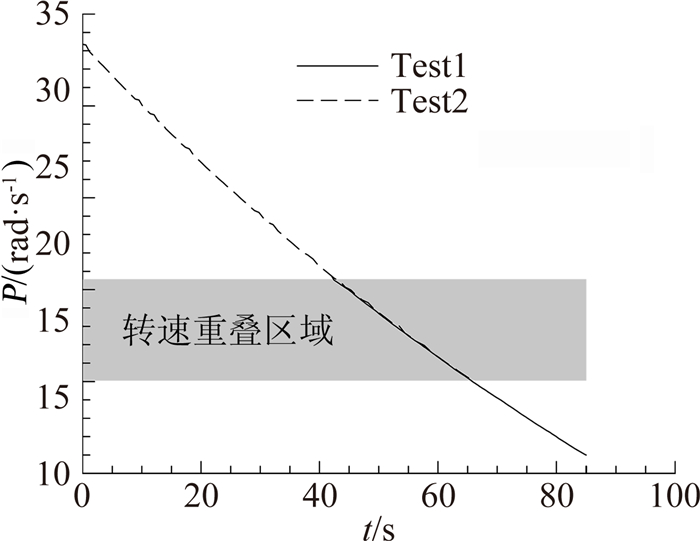| 图 8 不同车次平均转速变化曲线 (边条外形，α=0°)Fig. 8 Time courses of average rolling rate (body with strake, α=0°) |
图 9、图 11和图 12显示了不同模型，不同迎角下的最终试验结果。首先分析滚转阻尼力矩，两种模型Clp随迎角的变化见图 9。由图 9中的结果可以看到，Clp数据大小合理，符合基本物理规律：模型配装的突起物越大，Clp越大，配平翼模型的Clp量级比边条模型高约一个量级。
 |
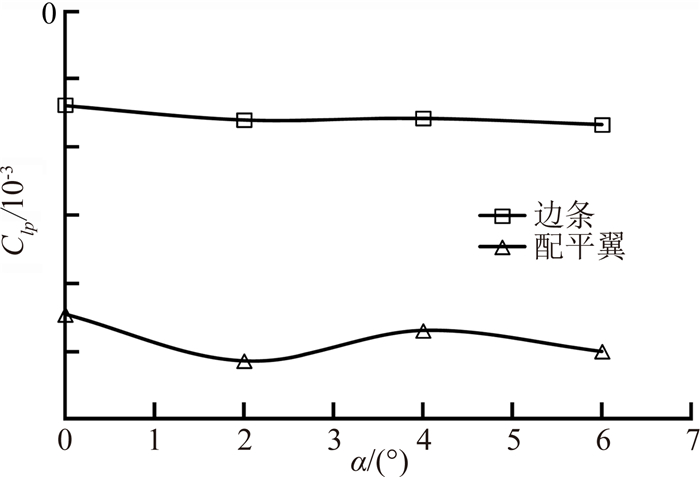| 图 9 Clp变化曲线Fig. 9 Experimental results of Clp |
 |
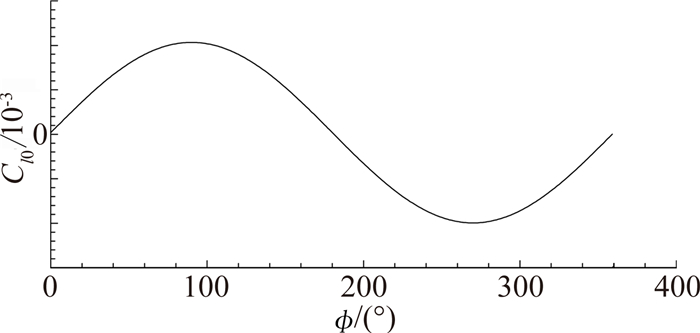| 图 10 Cl0变化曲线 (配平翼外形，α=6°)Fig. 10 Experimental results of Cl0 (body with trimming wings, α=6°) |
 |
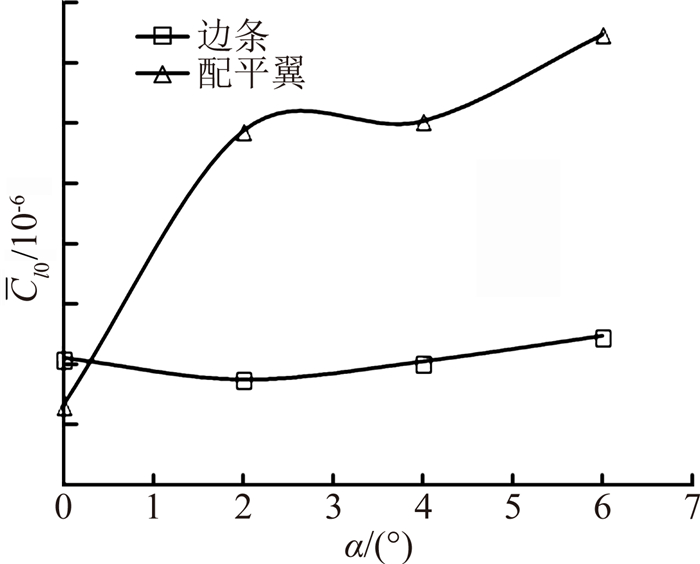| 图 11 Cl0变化曲线Fig. 11 Experimental results of Cl0 |
滚转静力矩Cl0的均值 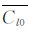和波动幅值A也得到了有效测量和区别。图 10以配平翼外形、α=6°为例，显示了Cl0随滚转角的正弦变化。由于两个模型均不存在滚转舵偏作用，理论上模型旋转一周后各滚转角位置滚转静力矩相互抵消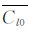，应为零。但注意到如图 10所示，Cl0的变化幅度A的量级相对较大，存在最小二乘拟合误差、大数平均误差等数据处理中带来的计算误差；同时考虑模型安装、边条和配平翼加工等其他因素，因此Cl0为一小数。根据图 11和图 12中结果可以看到，变化幅度A越大，此误差就越明显。当模型迎角为零时，理论上 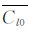不随滚转角变化而变化，但存在模型安装误差、边条和配平翼加工精度、多孔光栅加工不对称等因素，同时由于模型尺寸较大，进行风洞试验时模型-支杆系统会有微小的弹性形变和结构性振动，使Cl0产生微小周期性波动，数据处理后波动幅度A为一小数。
 |
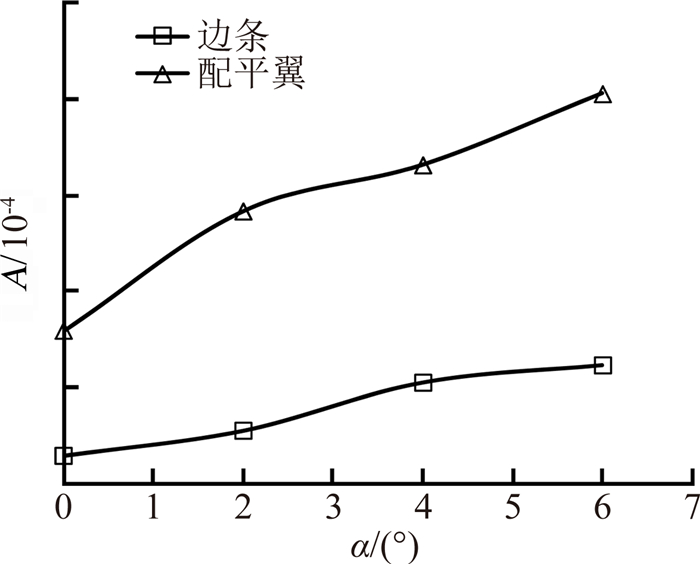| 图 12 A变化曲线Fig. 12 Experimental results of A |
当模型迎角不为零时，Cl0随滚转角产生正弦规律变化，其波动幅值A的结果如图 12所示。根据图 12结果可见，迎角越大，Cl0的波动幅度A越大，与理论分析中工程估算所预测的规律一致。图 13给出了迎角α=6°时，配装配平翼外形模型试验与仿真计算的P~t曲线。图中结果明确了Cl0正弦规律变化所产生的模型转速波动现象。同时可以看到，完整运动方程的仿真结果与试验结果吻合很好，再次验证了本文所建立气动力模型的合理性。
对于模型转速变化曲线和滚转静力矩系数正弦波动变化幅值A的数据处理，需要重点讨论和说明的是：如图 13所示，以配平翼外形、α=6°为例，模型转速较大时(P>40rad/s)，转速曲线波动较不明显；转速逐渐下降后(25rad/s <P<40rad/s)，其波动越来越显著；当转速较小时(P<25rad/s)，波动特征变得非常明显。原因可解释如下：当转速P较大时，滚转控制方程中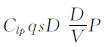 
项较大、(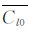+AsinΦ)qsD相对较小，因此滚转力矩波动幅值A不容易在转速曲线变化中体现；当转速P逐渐下降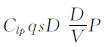，项逐渐减小,而 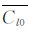+AsinΦqsD所占比重逐渐增加，其带来的转速波动变化就越来越明显。(若进一步考虑极端情况P=0，则滚转运动方程简化为静力矩平衡方程，描述常规静态测力试验，试验结果将只体现Cl0的作用而无Clp的作用)。根据以上分析可知，A的最终试验结果采用类似Clp和 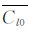的各转速段车次结果进行平均处理的方法是欠佳的，对转速较低的试验数据区域进行仿真匹配更容易得到相对准确的结果，换言之，转速范围较低的车次或转速较低的试验数据区域所计算出的滚转力矩系数波动幅值结果比高转速下的结果更为准确和可信。
本文中基于气浮轴承技术的风洞测量系统能够满足对机动式再入弹头小滚转气动力的精细、准确化测量。试验数据大小合理，规律性好，能够在准确测量滚转阻尼系数和平均滚转静力矩的基础上，获得烧蚀和安装配平翼等外形不对称产生的滚转静力矩波动变化规律和幅值。
理论分析和试验结果表明，正弦函数气动模型能够很好的描述Cl0的变化。原因在于：Cl0的变化与滚转角有关，而滚转角的变化规律正是周期性的三角函数。
理论分析和动力学仿真计算在辅助试验数据处理的同时很好的验证了试验结果。多种方法相互验证，完善了小滚转气动力测量的综合性风洞试验技术。
| [1] | Glover L S, Hagen, J C. The motion of ballistic missiles[R]. AD731662, 1971. |
| [2] | Fu Guangming, Feng Mingxi. Experiment for rolling aerodynamic damping of slight asymmetric re-entry body. Beijing:BeijingInstitute of Aerodynamics, 1996.(in Chinese)付光明, 冯明溪. 小不对称弹头滚转气动阻尼试验[R]. 北京:北京空气动力研究所, 1996. |
| [3] | Jiang Zhongdong, Zhao Zhongliang, Wang Suming, et al. Research on the measurement techniques for micro rolling moment in a hypersonic wind tunne[J]. Acta Aeronautica et Astronautica Sinica, 2001, 22(6):486-490.(in Chinese)蒋忠东, 赵忠良, 王树民, 等. 高超声速风洞小滚转力矩测量技术研究[J]. 航空学报, 2001, 22(6):486-490. |
| [4] | Williams E P. Experimental studies of ablation surface pattern and resulting roll torques[J]. AIAA Journal, 1971, 9(7):1315-1321. |
| [5] | Swaim C E. Aerodynamics of re-entry vehicle with asymmetric nosetip shape change[R]. AIAA-77-782, 1977. |
| [6] | Bai Kui, Feng Mingxi, Fu Guangming. Experiment technique for rolling aerodynamic of slight asymmetric re-entry body[J]. Experiments and Measurements in Fluid Mechanics, 2002, 16(3):63-72.(in Chinese)白葵, 冯明溪, 付光明. 小不对称再入体滚转气动力测量技术[J]. 流体力学实验与测量, 2002, 16(3):63-72. |
| [7] | Ma Qiang. Aerodynamic desigh of re-entry vehicle. Mianyang:China Aerodynamics Research and Development Center, 2005.(in Chinese)马强. 再入飞行器气动设计[D]. 绵阳:中国空气动力研究与发展中心, 2005. |
| [8] | Petsopoulos T, Regan F. A moving-mass roll control system for a fixed-trim re-entry vehicle[R]. AIAA Paper 1994-0033. |
| [9] | Zhang Hongjun, Chen Yingwen, Zhang Weimin. Research on aerodynamics characteristic of hypersonic high lift-drag ratio vehicle based on engineer rapid prediction method[J]. Tactical Missile Technology, 2011,(1):37-43.(in Chinese)张红军, 陈英文, 张卫民. 基于工程快速计算方法的高超声速高升阻比飞行器气动特性研究[J]. 战术导弹技术, 2011,(1):37-43. |
| [10] | Ling Fuhua. A numerical treatment of the periodic solutions of non-linear vibrations systems[J]. Applied Mathematics and Mechanics, 1983, 4(4):489-506.(in Chinese)凌复华. 非线性振动系统周期解的数值分析[J]. 应用数学与力学, 1983, 4(4):489-506. |
| [11] | Wang L W, Zhang Y, Feng J F. On the euclidean distance of images[J]. IEEE Transactions on Pattern Anaysis and Machine Intelligence, 2005, 27(8):1334-1339. |
| [12] | Kheir N A, Holmes W M. On validating simulation models of missile systems[J]. Simulation, 1978, 30(4):117-128. |