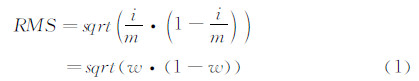0 引 言
边界层转捩问题一直以来都是理论和工程应用研究的热点话题。通常使用缩比模型对直升机螺旋桨进行气动力实验研究,由于存在尺度效应,实验模型边界层转捩位置与全尺寸情况下不同。导致实验测量的一些气动力系数存在误差,例如悬停效率、力矩系数等[1]。因此需要采用固定转捩的方法来模拟全尺寸旋转叶片的表面流态。对于固定翼飞机风洞实验,目前通常使用离散柱状粗糙元(Distributed Roughness Elements,DRE)进行固定转捩。DRE具有规范性、使用方便等优点,适合应用于直升机旋转叶片实验。一方面,为了充分促使边界层转捩,DRE尺寸应足够大,另一方面,还要求DRE产生最小的附加阻力。由于直升机转子运动的特殊性,针对旋转叶片开展粗糙元诱发转捩问题的研究十分必要。
早期关于粗糙元诱发转捩问题的研究以风洞实验为主[2, 3],且主要集中在平板或固定翼飞机模型实验方面。Schubauer和Klebanoff[3]在开展边界层转捩机理研究时,为了研究湍流斑发展特性,在低速风洞中使用热线测量了单个圆柱形粗糙元产生的湍流楔流场特征。气动力研究与发展中心的黄勇等[4]针对跨声速风洞实验模型开展了离散柱状粗糙元的固定转捩模拟技术研究。
近年来,随着计算资源与能力的迅速发展,越来越多的研究者使用直接数值模拟技术(DNS)开展边界层转捩问题的研究。同时,针对高、低速域内粗糙元诱发转捩问题开展了许多计算研究工作[5, 6, 7, 8]。尽管DNS可以提供流动结构的详细信息,但是需要占用巨大的计算资源,而且粗糙元诱发转捩问题涉及较多的因素,个别的研究只能考虑其中小部分因素。
实验研究的关键在于对转捩位置的准确测量,目前已有大量的非接触式边界层转捩测量技术投入工程应用,主要包括油膜干涉法、温度敏感涂层(TSP)、红外热像技术(IRT)等。油膜干涉法曾在风洞试验中用于全尺寸倾转旋翼测量[9]以及高速螺旋桨叶片测量[10]。TSP技术也应用于高速旋转螺旋桨叶片测量[11]。
红外技术最早于20世纪60至70年代开始应用,由于当时红外相机的灵敏度相对较差,主要用于再入飞行器的高温高焓气动实验[12]。随着红外相机技术的发展,IRT推广至对流换热测量[13],以及各类风洞实验中[14, 15]。Zuccher和Saric[16]以及Crawford等[17]在风洞以及飞行实验中开展了红外边界层转捩测量研究,并提出基于统计原理的转捩位置判定方法。Mori等[18]首次将IRT用于转子叶片边界层转捩测量。最近,红外热像技术已成功应用于悬停状态下缩比及全尺寸直升机转子边界层转捩测量[19, 20],同时Raffel等[20]提出适用于俯仰震荡翼型表面及转子叶片表面非定常转捩位置测量的DIT技术。红外技术的优势在于其较高的温度分辨力(约为0.02K),而TSP技术的温度分辨力大约是0.1K[21]。
以往的研究工作主要集中于离散粗糙元在固定翼飞机边界层固定转捩模拟的应用,对于直升机转子方面的论述较少。本文针对旋转叶片表面圆柱形粗糙元诱发转捩问题进行实验研究,使用红外技术对单个及单排DRE下游边界层转捩进行测量,并提出基于湍流区面积比率的转捩位置判定准则,实现在热图中自动识别转捩位置,进而分析不同粗糙元尺寸对边界层转捩的影响规律。研究结果将为旋转叶片边界层转捩位置定量测量提供有效方法,同时为旋转叶片表面离散粗糙元设计提供参考依据。
1 红外热像技术(IRT)探测转捩 1.1 基本原理IRT通过探测模型的红外辐射测量模型表面温度分布。根据温度分布可判断模型表面的传热特性,利用IRT探测转捩就是基于边界层转捩过程中两种传热现象之一[19]。
对于高Ma数和高温实验,模型表面温度分布取决于恢复因子,湍流的恢复温度高于层流,第一种边界层转捩位置的判断方法基于湍流边界层的恢复温度高于层流[22, 23]。但是对于亚声速实验或者模型温度与环境温度接近,可测的温度差非常小。第二种转捩探测方法基于湍流边界层的传热系数高于层流。由于对流换热系数与表面摩擦切应力成正比,湍流边界层的对流换热系数比层流的大,当来流与模型之间存在温度差时,湍流区的模型表面将更快地接近气流温度,使得层流与湍流区之间形成温差。可通过加热模型的方式提高模型与来流间的温差,通常使用热阻丝或卤素灯加热模型[17, 20]。
1.2 实验方法实验前在模型表面喷涂一层黑漆,确保模型表面发射率大于0.7,由于黑漆涂层的厚度不超过20μm,相对于模型厚度是小量,可认为不影响表面流动。
产生模型与气流之间的温差,通常的有三种方法:a在模型外部使用卤素灯烘烤模型;b在模型内部镶嵌加热电阻;c在实验前提高模型温度,产生模型与气流之间的初始温度差。本文实验中,使用卤素灯加热模型。
用归一化的灰度图像表征模型表面温度,I/Imax=0代表黑色的像素,I/Imax=1代表白色的像素。
1.3 转捩判定准则图 1左侧是典型的带有DRE的模型表面热图,DRE下游的转捩图案呈锯齿状。在这种情况下,不应该以某一剖面的转捩点作为整个叶片的转捩位置,因此需使用合适的转捩判定准则。
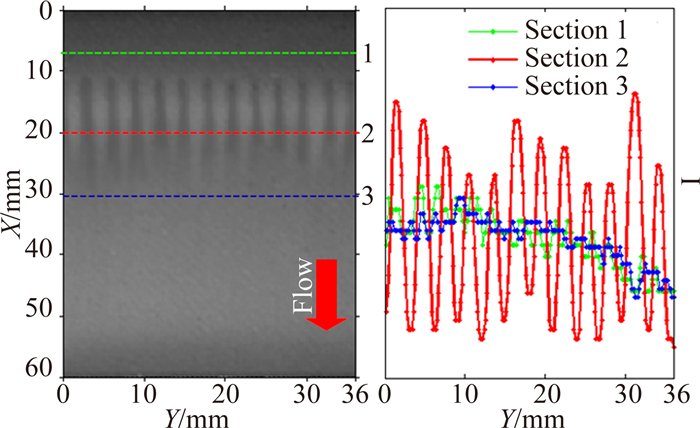 |
| 图 1 边界层转捩前后温度分布对比Fig. 1 Typical transition pattern downstream the DRE |
图 1右侧的灰度值曲线是从热图中的三个剖面提取得来,剖面1、2、3分别位于层流区、转捩区及湍流区。可以看出,当流动完全为层流或湍流时,灰度值分布较均匀,变化幅值相对较小;在转捩过程中,剖面2的灰度分布呈波峰波谷状(peak-valley pattern),变化幅值相对较大。因此,可根据流动方向各剖面的灰度变化幅值判断边界层转捩。
如图 2所示,假定了一个理想的DRE下游边界层转捩图案。假设粗糙元是一个点,由每个粗糙元产生的湍流楔交错形成相邻粗糙元之间的三角形层流区,红色三角代表层流区,令该区域内温度皆为0;下游区域代表湍流,令湍流区内温度值皆为1。任意取某个X方向剖面,得到一列周期性方波数据,令i代表层流区长度,m代表一个周期的长度。令w=1-i/m,表示湍流区域占剖面总长度的比例,w=0~1,因此可以用于表征湍流边界层的发展程度,w=0表示完全层流,w=1表示完全发展的湍流。
 |
| 图 2 DRE下游边界层转捩理想模型Fig. 2 Ideal boundary layer transition pattern downstream DRE |
任意X向剖面曲线的均方根计算公式为:
由公式(1)可知,RMS曲线的峰值出现在w=0.5处,且Rmax=RMS(0.5)=0.5。为了方便处理,以w=0.8为转捩终点的判定阀值,当w=0.8时R80=RMS(0.8)=0.4,此时R80/Rmax=0.8,说明转捩点位于RMS曲线峰值80%所在位置。这种情况下,可根据RMS曲线确定转捩位置。
如图 3所示,说明转捩位置判定的基本过程,首先计算各X向剖面的温度RMS值,得到RMS-X曲线(见右侧曲线);然后判断RMS曲线峰值Rmax,计算R80=0.8×Rmax,R80对应的X坐标就是边界层转捩位置,结果如图中红色虚线所在站位。为了方便论述,下文中将称这种转捩判据为R80准则。
 |
| 图 3 边界层转捩位置判据示意图Fig. 3 Sketch of boundary layer transition position detection |
实验在中航工业气动院的直升机旋转叶片模拟装置上进行,使用叶片为航模直升机用螺旋桨。叶片转盘半径为R=800mm,弦长C=60mm,测量区域为叶片下表面。实验中,旋转叶片的总距为0。
如图 4所示,实验系统由转子叶片、两个350W卤素灯、红外相机、光电传感器组成。红外相机为FLIR SC7750L型,MCT-探测器,可用波段为8~9.4μm,像素分辨率为640×512。红外相机位于转子下方,用于获取转子下表面温度分布,为了减弱叶片成像模糊,曝光时间IT=100μs。实验中,利用光电传感器对叶片位置进行锁相,触发红外相机工作,使叶片出现在红外相机的FOV中间。两个卤素灯用于提高叶片表面温度,使得叶片与气流之间的温差约为8℃,实验时大气温度约为10℃。
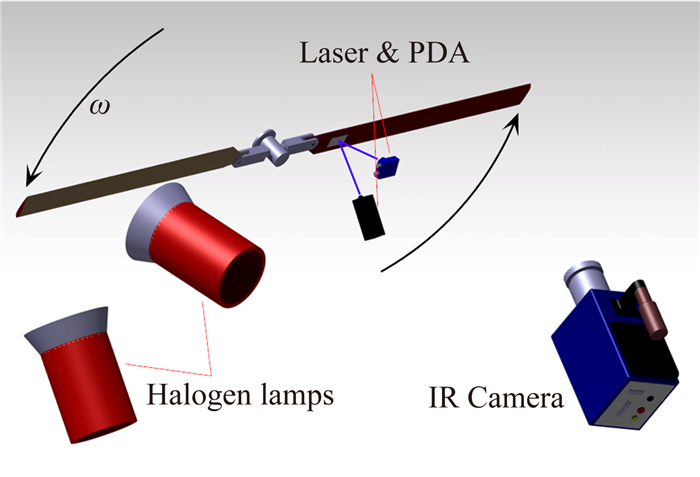 |
| 图 4 实验系统示意图Fig. 4 Sketch of the experiment system |
本文使用的是圆柱型DRE,主要有三个尺寸参数,分别是d、k和l。其中,d为圆柱粗糙元的直径,k是粗糙元高度,l是两粗糙元的间距。
通过不干胶模切工艺加工,粗糙元材料为PVC薄膜。如图 5所示,DRE布置于弦向20%处,布置范围约为r/R=0.9~0.98,红外相机主要观测叶尖区域,主要测量范围大约是r/R=0.85~1,由于DRE的径向布置范围为70~78mm,本文以75mm为参考半径计算叶尖切线速度。
 |
| 图 5 模型表面的柱状粗糙元, k=0.125mm, d=1.2mm, l=2.5mmFig. 5 DRE used in current study, k=0.125mm, d=1.2 mm, l=2.5mm |
主要实验状态列于表 1中。
| CASES | size of DRE/mm | fixed transition location |
| 1 2 3 4 5 6 7 8 | k=0 k=0.125, l=2.5 k=0.15, l=2.5 k=0.20, l=2.5 k=0.25, l=2.5 k=0.25, l=3.0 k=0.25, l=3.6 single k=0.25 | free transition X/C=0.20 X/C=0.25 X/C=0.20 X/C=0.20 X/C=0.20 X/C=0.20 X/C=0.20 |
首先,进行自由转捩实验,目的是提供基本状态;
其次,在叶片表面X/C=0.2处布置单个粗糙元,d=1.2mm,k=0.25mm,旋翼转速300~600r/m。测量粗糙元下游湍流楔角度,并估算单排DRE下游边界层转捩位置,用于验证实验测量值;
最后,为了分析DRE的各尺寸参数对边界层转捩的影响,选用的DRE尺寸参数为:d=1.2mm,k=0.125~0.25mm,l=2.5~3.6mm。
考虑到湍流度的影响,实验中测量了旋转叶片尾流的湍流度。使用单丝热线探针,热丝置于距离叶片转盘下方20mm处(防止旋转叶片击打探针),测量叶尖切向速度。能够采样频率为10kHz,采样时长为3.5s。计算湍流度时,采用的参考速度为叶尖切速度。
3 结果与讨论为了方便讨论,首先明确一些参数的符号。V是叶片半径r=750mm处的切线速度,C是叶片弦长。Xtr=X/C是边界层转捩位置,Ltr是转捩长度,为实际转捩位置与DRE的X方向间距,自由转捩时Ltr=Xtr×C。
转捩长度雷诺数ReLtr=ρ·V·Ltr,粗糙元高度雷诺数Rek=ρ·V·k。
3.1 自由转捩根据自由转捩探测结果(具体参数见表 2),计算转捩长度Ltr以及基于Ltr的雷诺数ReLtr,并画出ReLtr-ReC的曲线图(图 6),可以看出,自由转捩长度雷诺数与弦长雷诺数呈线性关系。
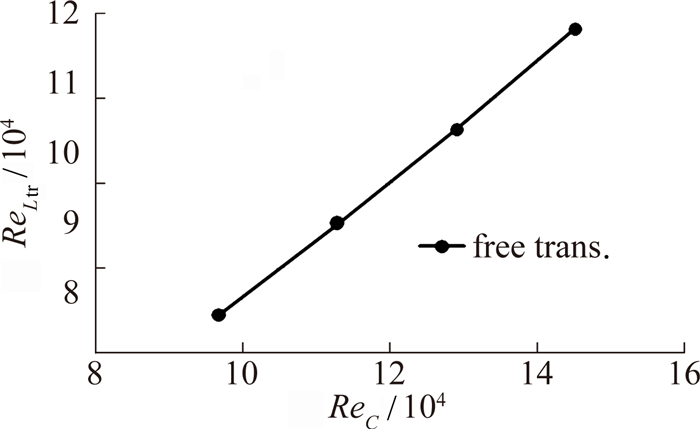 |
| 图 6 ReLtr-ReC曲线,自由转捩Fig. 6 The ReLtr vs. ReC curve |
在层流区域放置一个足够大的粗糙元,流动将在粗糙元处开始转捩,并在下游形成一个楔形的湍流区域[3]。本研究测量了单个圆柱粗糙元产生的湍流楔角度。根据前面假设,单排DRE下游转捩图案呈锯齿形状,可根据DRE间距及湍流楔角度估算下游的转捩长度,估算结果可用于验证转捩位置测量结果。
Schubauer和Klebanoff[3]为了研究湍流斑发展机理,在平板上距前缘609.6mm处放置单个直径1/8in圆柱形粗糙元,风速为24.38m/s,ReX大约是84 800,测得湍流楔半角θ/2=6.4°~10.6°,并使用热线测量湍流发展区域的流场细节。
将单个圆柱形粗糙元(d=1.2,k=0.25mm)放置在叶片弦向X/C=0.2处,V=23.56~35.34m/s,对应的ReX=19 400~29 000。实验结果如图 7所示,首先使用canny算子提取热图中的边缘,通过hough变换检测直线确定湍流楔的两条边缘直线,最后计算两条直线的夹角,即湍流楔角θ,测量结果为θ=6.13°~9.98°。θ随ReX增大,由于本文研究中的ReX较小,从趋势上看,测量结果是与Schubauer和Klebanoff[3]的结论是相符的。
 |
| 图 7 单个粗糙元诱发湍流楔的测量Fig. 7 Turbulent wedge induced by single roughness element, k=0.25mm, d=1.2mm |
根据实验测得的湍流楔角,可估算单排DRE下游的转捩长度。图 8对比了利用本文方法判断的转捩长度与估算值,实验值与估算值的变化趋势是一致的,说明本文的测量结果是可信的,并且本文方法适用于带有DRE的边界层转捩位置测量。
 |
| 图 8 转捩长度估算与实际值对比 (d=1.2mm, k=0.25mm, l=3.6mm)Fig. 8 Comparison of transition position, (d=1.2mm, k=0.25mm, l=3.6mm) |
表 2中列出了主要状态的边界层转捩测量结果,随着速度的增加,转捩位置逐渐提前;随着DRE高度的增加,转捩位置提前。由于实验使用的粗糙元间距范围有限,尚不能分析粗糙元间距对转捩位置的影响。
| V (m·s -1) | Turb. Degree | free trans. | transition position Xtr ( X/C) DRE located at x/C=0.2, l=2.5 | ||
| k=0.125 | k=0.2 | k=0.25 | |||
| 23.56 | 0.012% | 0.873 7 | 0.758 5 | 0.654 5 | 0.539 9 |
| 27.49 | 0.012% | 0.843 6 | 0.734 6 | 0.540 9 | 0.427 5 |
| 31.42 | - | 0.824 | 0.695 3 | 0.453 2 | 0.391 |
| 35.34 | - | 0.814 1 | 0.628 3 | 0.385 8 | 0.362 5 |
图 9给出了是各种DRE诱发转捩长度雷诺数ReLtr曲线,横坐标是基于弦长的雷诺数ReC,对于k=0.125mm的工况,当ReC<1.3×105时ReLtr随着ReC增大,可能是由于DRE提供的扰动不够强大,边界层最初保持了自由转捩的趋势(图 6),当风速较大时扰动促使转捩的效果越来越明显。说明诱发层流转捩所需的临界扰动量随风速的增加而减小。
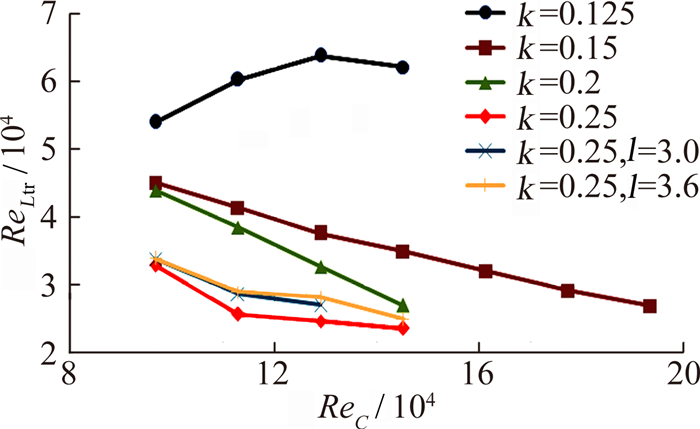 |
| 图 9 ReLtr-ReC 曲线Fig. 9 ReLtr vs. ReC curve |
除了h=0.125mm的工况之外,所有曲线的趋势都是ReLtr随ReC减小,当k=0.15和0.2mm时,ReLtr与ReC呈线性关系,且下降斜率是增大的;然而,k=0.25mm时,尽管转捩提前量大幅增加,但其促使转捩的效率明显降低,曲线大约在ReC=1.1×105处发生转折,且随着DRE间距的增加,转捩提前量呈减小趋势。
图 10是转捩长度雷诺数ReLtr随Rek的变化曲线,在不同Rexf时,ReLtr都随着Rek增大而减小,且随着Rexf增大,ReLtr曲线的斜率逐渐增大,说明粗糙元诱发转捩的效率是逐渐提高的。当Rek大约超过470时,曲线发生偏折,效率大幅降低。虽然转捩没有立即发生在粗糙元当地,但是在这种情况下,最优的Rek大约在470~600之间,对应的DRE高度h=0.15~0.25mm。
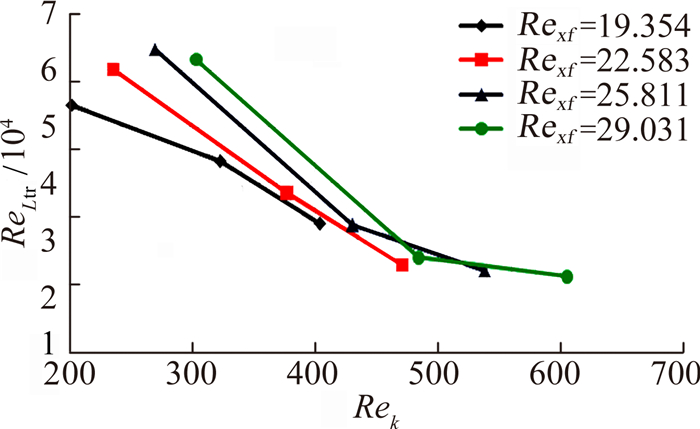 |
| 图 10 ReLtr-Rek曲线Fig. 10 ReLtr vs. Rek curve |
综合前面几组数据的分析认为,在ReX=16000~40000状态下,最优的DRE尺寸参数为:k=0.15~0.2mm,l=2.5mm,d=1.2mm。
4 结 论本文基于红外热像技术测量旋转叶片边界层转捩位置,提出一种转捩位置判定算法,并研究不同尺寸DRE对转捩位置的影响,主要得到以下结论:
(1)使用红外热像技术,实现了对低转速旋转叶片边界层转捩位置的探测,为旋转部件表面转捩探测提供了一种有效方法;
(2)针对DRE下游转捩位置判断,提出基于层流/湍流区面积比的转捩位置判断准则,通过实验验证,结果稳定可靠,因此具有一定的工程应用价值;
(3)在较低雷诺数状态下,初步得到了不同高度DRE诱发转捩位置与雷诺数之间的关系,随着粗糙元高度的增加,转捩位置逐渐靠前;
(4)关于粗糙元直径与间距对转捩位置影响的研究还不够充分,有待在后续的研究中展开讨论。
| [1] | Yang Y D, Yang J, Yuan H G. Investigation of the Reynolds number effect on the rotor hover performance[J]. Journal of Experiments in Fluid Mechanics, 2008, 32(4):11-14.(in Chinese)杨永东, 杨炯, 袁红刚. 旋翼悬停性能的Re数影响研究[J]. 实验流体力学, 2008, 32(4):11-14. |
| [2] | Dryden H. Review of published data on the effect of roughness on transition from laminar to turbulent flow[J]. Journal of Aeronautic Science, 1953, 20:477-482. |
| [3] | Schubauer G B, Klebanoff P S. Contributions on the mechanics of boundary-layer transition[R]. NACA-TN-3489, 1955. |
| [4] | Huang Y, Qian F X, Yu K L, et al. Experimental research on boundary layer fixed transition by distributed roughness elements[J]. Journal of Experiments in Fluids Mechanics, 2006, 30(3):59-62.(in Chinese)黄勇, 钱丰学, 于昆龙, 等. 基于柱状粗糙元的边界层人工转捩试验研究[J]. 实验流体力学, 2006, 30(3):59-62. |
| [5] | Bernardini M, Pirozzoli S, Orlandi P. Compressibility effects on roughness-induced boundary layer transition[J]. International Journal of Heat and Fluid Flow, 2012, 35:45-51. |
| [6] | Choudhary M, Li F, Wu M, et al. Laminar-turbulent transition behind discrete roughness elements in a high speed boundary layer[R]. AIAA 2010-1575, 40th Fluid Dynamics Conference and Exhibit. Orlando, Florida. |
| [7] | Piot, E Casalis G, Rist U. Stability of the laminar boundary layer flow encountering a row of roughness elements:Biglobal stability approach and DNS[J]. European Journal of Mechanics B/Fluids, 2008, 27:684-706, doi:10.1016/j.euromechflu.2008.01.007. |
| [8] | Rizzetta D, Visbal M. Direct numerical simulations of flow past an array of distributed roughness elements[J]. AIAA Journal, 2007, 45:1967-1976. |
| [9] | Wadcock A J, Yamauchi G K, Driver D M. Skin friction measurements on a hovering full-scale tilt rotor[J]. J.Am Helicopter Soc, 1999, 44(4):312-319. |
| [10] | Schülein E, Rosemann H, Schaber S. Transition detection and skin friction measurements on rotating propeller blades[C]//28th AIAA aerodynamic measurement technology, ground testing and flght testing conference, New Orleans, Louisiana, USA. Paper AIAA 2012-3202. doi:10.2514/6.2012-3202 |
| [11] | Yorita D, Asai K, Klein C, et al. Transition detection on rotating propeller blades by means of temperature-sensitive paint[C]//50th AIAA Aerospace Sciences Meeting, Nashville, Tennessee, USA, Paper AIAA 2012-1187. doi:10.2514/6.2012-1187 |
| [12] | Schultz D L, Jones T V. Heat transfer measurements in short-duration hypersonic facilities[R]. AGAR Dograph 165, AGARD-NATO, 1973. |
| [13] | Astarita T, Cardone G, Carlomagno G M, et al. A survey on infrared thermography for convective heat transfer measurements[J]. Optics and Laser Technology, 2000, 32(7-8):593-610. |
| [14] | Luca L D, Carlomagno G M, Buresti G. Boundary layer diagnostics by means of an infrared scanning radiometer[J]. Experiments in Fluids, 1990, 9(3):121-128. |
| [15] | Sant Y L, Marchand M, Millan P, et al. An overview of infrared thermography techniques used in large wind tunnels[J]. Aerospace Science and Technology, 2002, 6:355-366. |
| [16] | Zuccher S, Saric W S. Infrared thermography investigations in transitional supersonic boundary layers[J]. Experiments in Fluids, 2008, 44:145-157, doi:10.1007/s00348-007-0384-1. |
| [17] | Crawford B K, Duncan G T, West D E, et al. Quantitative boundary-layer transition measurements using IR thermography[C]//Proceeding of the 52nd Aerospace Sciences Meeting, National Harbor, Maryland, AIAA 2014-1411. doi:10.2514/6.2014-1411. |
| [18] | Mori M, Novac L, Sekavčnik M. Measurements on rotating blades using IR thermography[J]. Exp. Thermal Fluid Sci. 2007, 32(2):387-396. |
| [19] | Richter K, Schülein E. Boundary-layer transition measurements on hovering helicopter rotors by infrared thermography[J]. Experiments in Fluids. 2014, 55:1755, 1-13. doi:10.1007/s00348-014-1755-z |
| [20] | Raffel M, Merz C B, Schwermer T, et al. Differential infrared thermography for boundary layer transition detection on pitching rotor blade models[J]. Experiments in Fluids. 2015, 56(30):1-30. doi:10.1007/s00348-015-1905-y |
| [21] | Kowalewski T, Ligrani P, Dreizler A, et al. Temperature and heat flx. In:Tropea C, Yarin A L, Foss J F(eds) Handbook of experimental flid mechanics[M]. Berlin:Springer, 2007:488-553. |
| [22] | Peake D J, Bowker A J, Lockyear S J, et al. Non-obtrusive detection of transition region using an infrared camera[R]. AGARD CP-224, 1977. |
| [23] | Green M J, Budnik M P, Yang L, et al. Supporting flight-data analysis for space-shuttle orbiter experiments at NASA Ames Research Center[R]. NASA TM-84345, 1983. |
| [24] | Astarita T, Carlomagno G M. Applications. Infrared thermography for thermo-fluid-dynamics[M]. Springer Heidelberg, New York Dordrecht London, 2012. |
| [25] | Fey U, Egami Y, Engler R H. High Reynolds number transition detection by means of temperature sensitive paint[C]//44th AIAA Aerospace Sciences Meeting and Exhibit, 2006/doi:10.2514/6.2006-514 |