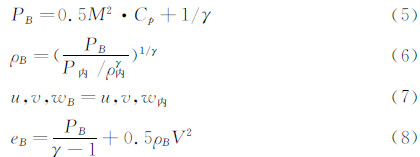0 引言
高速洞壁干扰修正技术历经发展,概括起来有以下修正方法:纯试验修正(单模型大小风洞对比法、多模型单风洞外推法)、经验修正(统计数据类推法)、映象法和Maskwell法、有限基本解法(涡格法、面元法)、壁压信息法(双参数壁压信息积分法、单参数壁压信息法)和基于CFD的非线性修正法等。
国内从20世纪80年代开始,采用壁压法对高速试验洞壁干扰进行修正,范召林等在FL-21风洞中先后进行了一系列二维和三维的风洞试验[1],研制出了适用于不同风洞的壁压测量装置,发展了一系列适三种跨声速洞壁干扰修正方法及其在小展弦比飞翼标模试验中的应用用于各种高亚声速风洞试验的线性洞壁干扰修正方法[2,3]。90年代,中国空气动力研究与发展中心高速所与总体技术部针对Ma=1附近洞壁干扰修正这一难题,开展了跨声速三维非线性洞壁干扰修正的研究[4,5,6],采用Euler方程和N-S方程模拟模型绕流场,以实测的透气壁附近的压力分布作为风洞流场的边界条件,数值求解风洞流场和自由流场,由两者之差得到洞壁干扰对模型气动力的影响,取得了令人满意的结果。此后,对数值模拟方法和网格生成技术的不断完善,将其应用范围不断扩展[7]。
2000年以后,国内外对洞壁干扰的研究主要围绕基 于CFD的非线性修正方法。GLASGOW大学计算流体动力试验室利用RANS方程求解器研究洞壁对三角翼涡产生、发展与破裂的影响[8]。日本空间探索局(JAAX)用含壁压信息的CFD非线性模拟手段研究ONERA M5翼身组合体洞壁干扰[9]。DNW采用CFD方法完全模拟了HST风洞的试验段、驻室和扩散段,并研究了不同尺度的DLR-F4机翼洞壁干扰特性[10]。
此外,波音公司一直致力于洞壁干扰的工程化修正方法,从早期的面元法程序PANAIR[11]到全速势方程求解器TRANAIR。利用TRANAIR开展了翼身组合体标模不同翼展模型洞壁干扰扰动速度和扰动迎角[12],试图建立洞壁干扰数据库,并用CFD++验证其不确定度[13]。
飞翼布局因高效、隐身等优点广泛地应用于现代飞行器设计中,而针对飞翼布局洞壁干扰修正方法的研究尚未开展。飞翼布局洞壁干扰与翼-身-尾常规布局是否有相同的规律性,传统方法的适用性如何,都值得深入分析。装备预研联合攻关项目“风洞试验技术”以小展弦比飞翼布局标模为研究对象,广泛开展相关试验技术的研究[14, 15, 16],其中包括洞壁干扰修正方法的研究。
为摸清飞翼标模洞壁干扰影响规律并研究洞壁干扰修正方法对飞翼布局的适用性,该项目在FL-24风洞进行了带壁压测量的测力试验,并在FL-26风洞进行了验证试验。本文除了利用小扰动位流壁压信息法和基于RANS的壁压信息法计算飞翼标模在FL-24风洞中的洞壁干扰修正量,还首次在国内建立了与波音公司类似的全速势位流方法并实现了洞壁干扰修正。通过对三种方法修正结果与试验结果的比较,综合评价三种方法的优缺点及在飞翼标模洞壁干扰修正中的适用性,为类似飞翼布局风洞试验洞壁干扰修正提供参考。
1 飞翼标模风洞试验 1.1 试验设备与方法飞翼标模采用单前缘融合体飞翼布局,前缘后掠角65°,后缘后掠角47°。试验模型为缩比1 ∶19的全金属模型,机身长度为0.806m,翼展0.602m,平均气动弦长为0.5032m。
中国空气动力研究与发展中心高速所FL-24风洞试验段尺寸1.2m×1.2m,跨声速试验段上下壁面为60°斜孔壁,开闭比为4.3%;左右为直孔壁,开闭比为21.4%;孔径和壁厚为12mm。飞翼标模采用尾支撑,前缘5%当地弦长处粘贴高度为0.12mm的柱状转捩带,零迎角时在FL-24风洞的堵塞度约为0.97%。试验分为无壁压管测力试验、安装壁压管空风洞试验和安装壁压管带模型测力试验。修正气流偏角后的无壁压条测力结果作为飞翼标模在FL-24风洞中的基准数据,带模型壁压减去相同Ma数空风洞壁压作为洞壁干扰修正用的壁压数据。共安装有12根壁压条,上下洞壁各4根、左右洞壁各2根,长度覆盖了从试验段入口到支架段区域。图 1给出了试验照片。
 |
| 图 1 FL-24风洞试验照片Fig. 1 FL-24 wind tunnel test picture |
中国空气动力研究与发展中心高速所FL-26风洞试验段尺寸为2.4m×2.4m,四壁都为斜孔壁,综合开闭比为4.3%。飞翼标模采用FL-24风洞相同的天平、支杆通过过渡接头安装在中部支架上,零迎角时堵塞度约为0.24%。修正气流偏角后的测力结果近似认为无洞壁干扰数据,与FL-24风洞数据之差作为FL-24风洞洞壁干扰试验结果。
 |
| 图 2 FL-26风洞试验照片Fig. 2 FL-26 wind tunnel test picture |
扣除空风洞后的壁压数据由于测压孔加工质量等原因仍会存在一定程度的跳动散布,可采用三次样条曲线进行光顺,然后使用样条插值法将壁压数据插值到风洞壁面处。图 3给出了Ma=0.8,壁压信息插值到整个风洞洞壁位置的压力系数分布图。可以看到,迎角4°时,模型上方为气流加速区,模型下方为减速区;迎角16°时,加速区和减速区范围增加、强度增强,并在侧壁上出现近似与模型平行的分界区域。
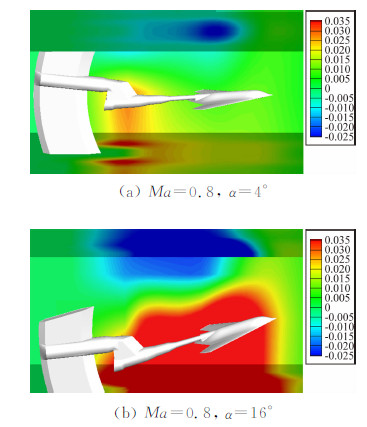 |
| 图 3 FL-24风洞壁压信息Fig. 3 Wall pressure signature in FL-24 wind tunnel |
飞翼标模气动特性是以涡的产生、发展与涡破裂为主导的,在跨声速阶段还伴随着涡与激波的交叉干扰。飞翼标模气动特性详细描述见参考文献[16],这里只给出FL-24风洞和FL-26风洞试验结果升力特性对比曲线。升力曲线可分为线性段、非线性涡升力段、涡破裂段和涡破裂后段。小迎角附着流状态为线性段,迎角4°左右开始产生前缘涡升力,升力系数呈非线性增加,12°左右涡破裂,升力曲线出现拐点,之后升力系数继续增加。
图 5给出了FL-26、FL-24风洞试验结果升力系数差量曲线。两风洞试验采用相同的天平与支杆,保证近场支撑干扰相似,试验结果均进行了气流偏角修正,可以认为两风洞数据差异是由洞壁干扰引起的。可以看出,飞翼标模洞壁干扰量与翼-身-尾组合体常规布局不同,而表现为随迎角变化有不同的发展趋势:在小迎角阶段,洞壁干扰量基本线性且随迎角增加向负向增加,在中等迎角开始,趋势反向,随迎角增加洞壁干扰量向正向增加。这与飞翼标模气动特性为涡主导的特点是密切相关的,洞壁干扰在线性段、涡升力非线性段、涡破裂不同阶段有不同的影响。需要指出的是,两座风洞升力曲线涡破裂迎角有差异,而涡破裂影响因素不仅与洞壁干扰相关,还与流场湍流度、不均匀度和远场支架干扰[15]等因素都有关。涡破裂后的气动特性是与涡破裂起始迎角密切相关的,因此涡破裂后两风洞试验结果的差量不能完全代表洞壁干扰影响,而是掺杂了其他因素的影响。
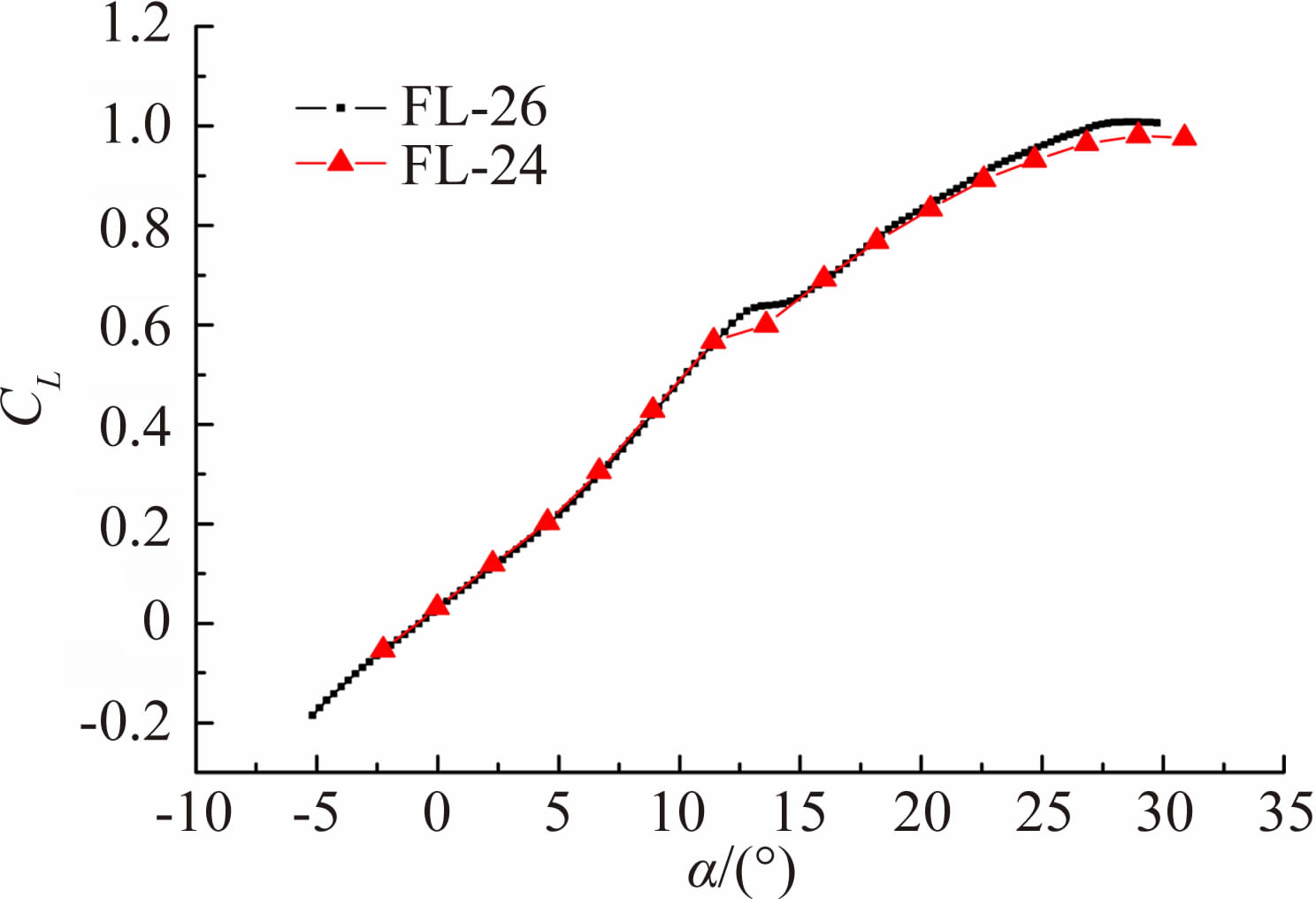 |
| 图 4 FL-24与FL-26风洞试验结果比较(M=0.8)Fig. 4 Comparison of test results in FL-24 and FL-26 |
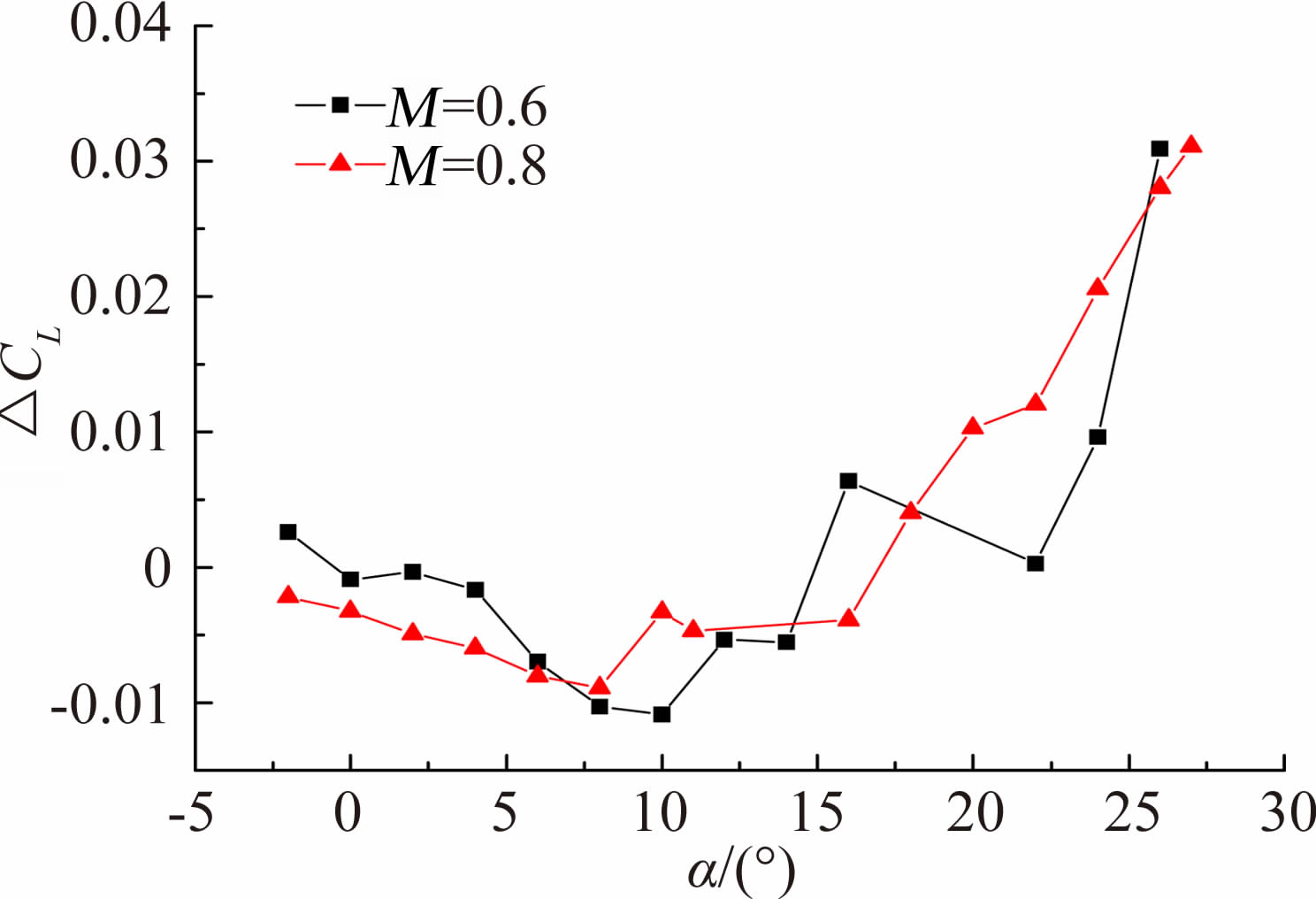 |
| 图 5 洞壁干扰验证试验结果Fig. 5 Wind tunnel wall interference validate test result |
小扰动位流壁压信息法是基于线化小扰动位势方程,根据模型、支杆等物面条件得到无洞壁存在情况下模型、支杆等网格的基本解强度,然后计算模型基本解与洞壁基本解在洞壁网格控制点出的诱导速度,根据壁面压力信息代替的洞壁边界条件,求解洞壁上基本解强度,从而得到洞壁对模型的干扰压力分布和干扰阻力,迭代该过程得到洞壁干扰的影响量。壁压条测量压力系数Cp,洞壁边界条件为:
式中Φm为模型引起的拢动速势。该边界条件与控制方程构成一个三维Dirichlet问题,可以采用偶极子面元法和有限差分法求解。
该方法经过多年工程化应用发展,形成了一套成熟的洞壁干扰修正软件,给定模型的参数信息、模型的气动力系数测量值及壁面压力系数测量值,可得到各气动力系数的洞壁干扰修正结果和模型上的扰动速度分布。其适用范围为Ma<0.9,试验迎角范围可达±90°,风洞壁可以是实壁或通气壁。模型参数默认为翼身尾组合体模型,飞翼布局只能近似设置。
2.2 全速势位流方法全速势位流方法的控制方程为:
根据给定的模型、支杆等物面网格,自动生成空间笛卡尔网格,数值求解控制方程与边界层方程得到无洞壁条件下的流场信息。壁面是通过面源和面偶极子奇点分布的模拟,由无洞壁条件下求取的壁面附近的速度场和特定壁面边界条件得到奇点强度,进而得到洞壁对模型的气动特性的影响。由于其控制方程为全速势方程,因此可应用于更高速度的跨声速流动,其Ma数应用范围为Ma < 1.0。
壁面区域的边界条件使用扰动速势Φ表示,实壁时:
开孔壁边界条件为:
其中R为透气壁参数,不同的透气壁参数R模拟不同的开闭比影响,R=0为实壁,无穷大时为自由流。R可通过由该方法计算得到的壁面压力与壁压条所测的壁面压力结果的吻合程度来估计。图 6为飞翼标模全速势位流方法模拟用网格,图 7给出了不同的R参数壁压计算结果与FL-24风洞壁压测量结果的对比曲线。可以看到,R=1时计算结果与试验结果吻合最好,这与FL-24风洞历史壁特性参数测量结果是一致的,可用来模拟FL-24风洞开孔壁。
 |
| 图 6 全速势位流方程方法用网格Fig. 6 Gird for full potential equation method |
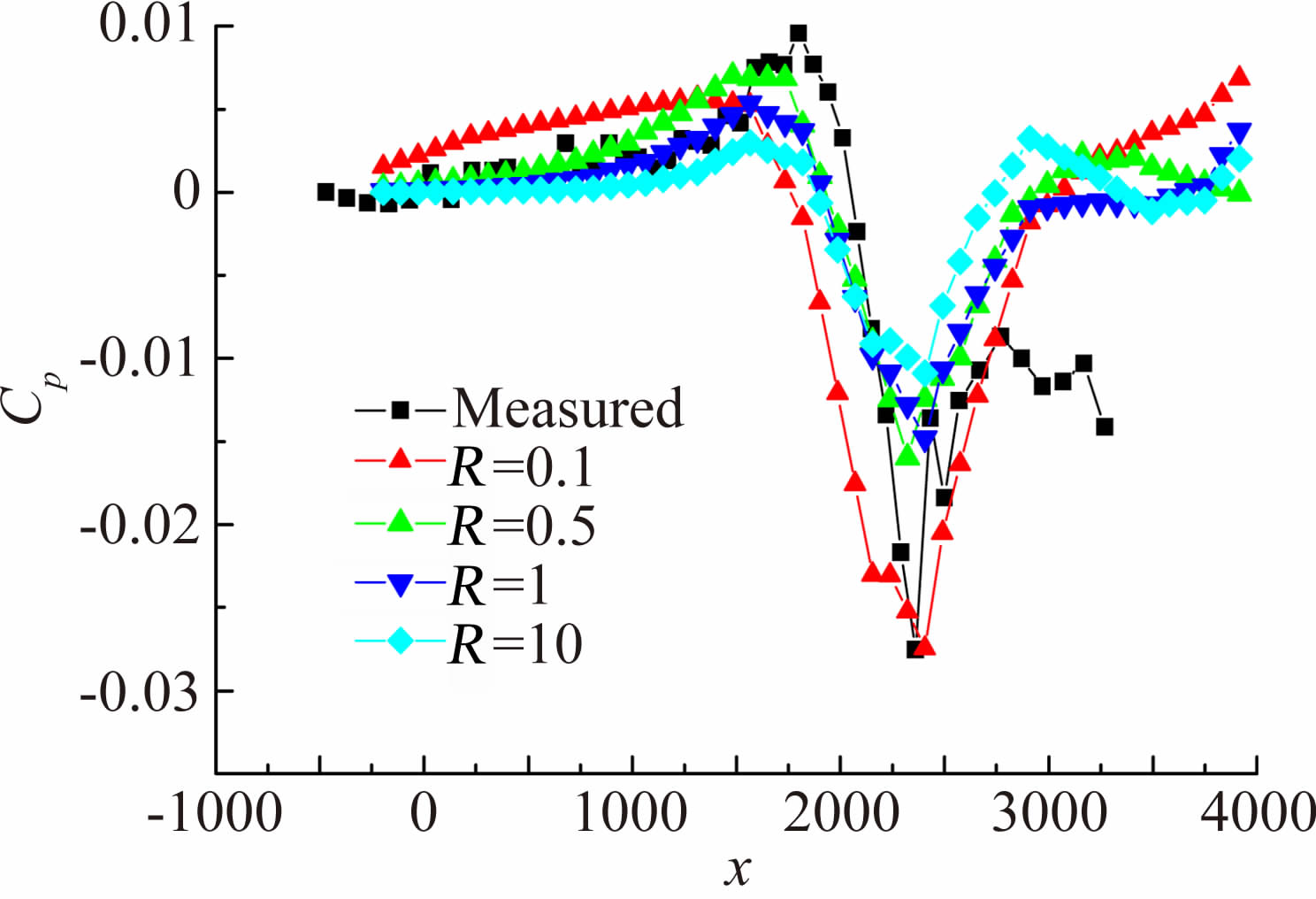 |
| 图 7 不同R参数壁压计算结果与测量结果比较Fig. 7 Comparison of variant R parameter calculation results and measured result |
基于RANS的壁压信息法在自主研发的多块结构网格求解器基础上融合了壁压信息边界条件处理方法,采用相同的控制方程和模型网格,分别以远场和试验测得壁压为边界条件,计算出模型自由流和洞壁存在时的表面力(力矩)系数,从而得到洞壁干扰量。求解器采用有限体积法,控制方程为雷诺平均N-S方程组,湍流模型为两方程k-w SST模型,为了加快收敛速度,采用了局部时间步长和多重网格技术。图 8给出了数值模拟结果与试验结果的对比曲线,可以看出,RANS求解器在升力曲线拐点前与试验结果吻合良好,拐点迎角比试验结果推后。
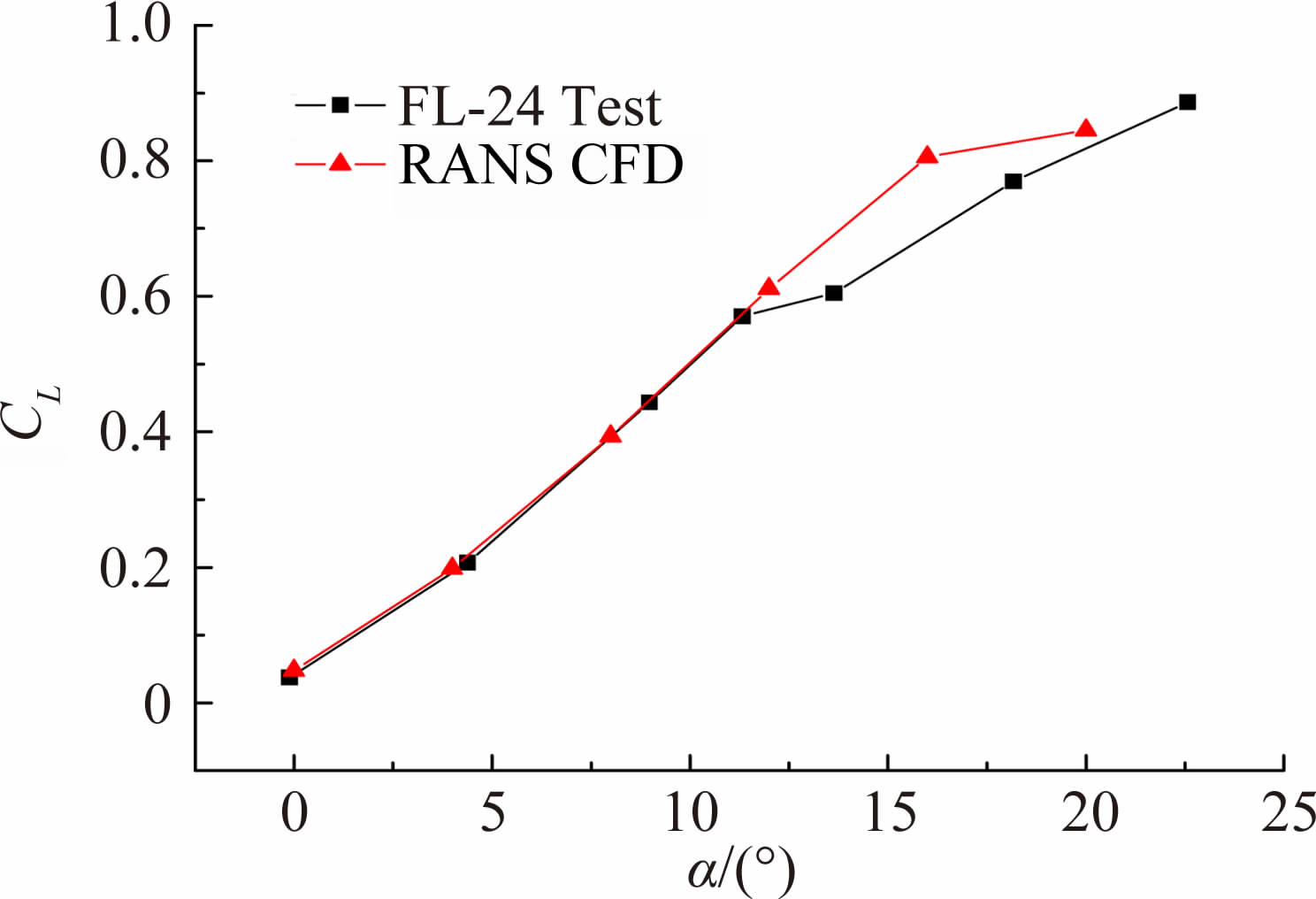 |
| 图 8 RANS CFD结果与试验结果比较Fig. 8 Comparison of RANS CFD and test results |
壁压信息处理需要将壁压条测得的壁压插值到洞壁边界计算网格点上,并将前后远场外插到0。洞壁边界条件为:
其中,下标B表示最外层边界网格,下标“内”表示内层网格。从理论上讲,由于这种方法的控制方程是非线性的,可以突破线性理论的限制,对于各种复杂流动均可以进行洞壁干扰修正。
2.4 洞壁干扰修正结果分析采用上述三种方法分别对小展弦比飞翼标模FL-24风洞试验结果进行洞壁干扰修正。图 9给出了三种修正方法洞壁干扰修正量与FL-26风洞验证试验结果的对比曲线。
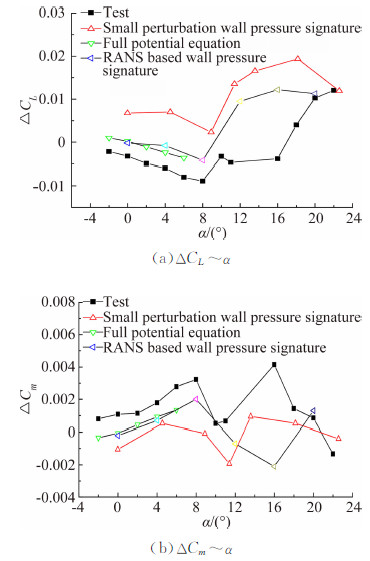 |
| 图 9 不同洞壁干扰修正方法结果比较Fig. 9 Comparison of variant wall interference correction method results |
可以看到,三种方法中,基于RANS的壁压信息法与全速势位流方法在线性段吻合良好,与试验结果趋势一致,量值略有差异,原因是试验结果同样存在误差,从规律上看,试验结果曲线偏下。试验结果中等迎角趋势反向问题在基于RANS的壁压信息法结果中同样有所反映,迎角12°后量值与试验结果差异较大,这与RANS求解器在涡破裂迎角的捕捉上与试验结果差异较大有关(见图 8)。传统的小扰动位流壁压信息法结果在趋势上能够保持一致,但量值差异稍大。这可能与该方法默认的模型为翼身尾组合体,与飞翼布局存在差异导致。
洞壁干扰在不同迎角范围内影响方式不同,整体看,存在三段不同影响区间。在迎角-2°~4°附着流为主要流态阶段,洞壁干扰的影响表现为上(下)洗流的影响和Ma数增量的影响。在4°~12°左右,模型上表面逐渐形成稳定的涡系,涡升力表现突出,升力呈现非线性增加,该阶段洞壁影响不再是洗流和Ma数增量影响,而是影响了涡的空间位置和强度,使得洞壁干扰量呈现反向增加趋势。在涡发生破裂后,洞壁影响更加复杂,试验结果存在诸多伪洞壁干扰因素,而计算结果难以捕捉涡破裂角度而存在较大误差。
为了分析洞壁干扰影响在不同角度出现趋势相反的问题,图 10给出了基于RANS方法得到的迎角8°与12°、有无洞壁模拟表面压力分布的对比云图。可以看出,在迎角8°,洞壁的存在使上下表面压力系数负值增加,12°时洞壁的存在却是使其负值减小。从8°与12°表面压力差异看,8°仅部分展向位置受涡的影响出现吸力鼓包。而在12°时,大部分展向位置出现压力鼓包,也就是说,12°迎角涡升力显著,此时,洞壁干扰修正量出现趋势反向,这在一定程度论证了洞壁干扰在不同迎角区间影响方式不同的说法。
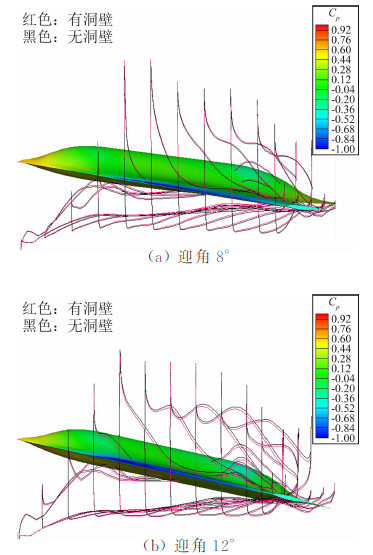 |
| 图 10 不同迎角有无洞壁模拟表面压力分布对比Fig. 10 Comparison of surface pressure distribution on different angles of attack with and without wind tunnel wall simulation |
不同风洞试验结果差异不仅仅表现在洞壁干扰上,来流湍流度、支撑干扰等都会有一定影响,因此,试验得到的洞壁干扰结果也并不能认为是真值所在。综合比较三种方法,可以得出:小扰动位流壁压信息法在量值上与其他结果相差较大,模型模拟方法需要针对飞翼布局进行改进;全速势位流方法在线性段能够捕捉规律,且量值与基于RANS的壁压信息法较为接近,计算模型构造简单,计算速度较快,而且不需要壁压信息;基于RANS的壁压信息法在壁面无强激波存、气流无大面积分离或者无涡破裂条件下,都能得到较为准确的结果,但该方法需要壁压信息,且空间网格质量要求较高,网格准备复杂,计算时间长。
| 方法 | 小扰动壁压信息法 | 全速势位流方法 | 基于RANS的壁压信息法 |
| 可靠性 | 不高 | 线性段良好 | 涡破裂前良好 |
| 壁压信息 | 是 | 否 | 是 |
| 计算时间 | 快 | 短 | 长 |
| 使用范围 | Ma<0.9 | Ma<1.0 | 壁面无强激波 |
本文采用了小扰动壁压信息法、全速势位流方法和基于RANS的壁压信息法针对小展弦比飞翼标模FL-24风洞试验结果开展洞壁干扰修正计算,通过与试验结果的比较,综合分析了三种方法的优缺点。结果表明:
(1) 飞翼标模洞壁干扰不同于翼-身-尾组合体布局,小扰动壁压信息法中模型的模拟方法需针对飞翼布局进行改进。
(2) 引入全速势位流方法评估洞壁干扰,该方法具备较强的工程实用性。
(3) 基于RANS的壁压信息法能在较大的范围内获得良好结果。
| [1] | 范召林, 恽起麟, 崔乃明.跨声速洞壁干扰修正的壁压法及其应用[J], 气动实验与测量控制, 1990, 4(4):45-51 |
| [2] | 范召林, 崔乃明, 恽起麟.壁压法应用于高速风洞大迎角试验洞壁干扰的修正[J], 空气动力学学报, 1991, 9(2):243-250. |
| [3] | 范召林, 尹陆平. 近声速测壁压试验研究[R]. CN-930262, CARDC-2, 1993. |
| [4] | 张玉伦, 陈作斌, 等. 实用外形亚跨超流场数值模拟研究[J]. 空气动力学学报, 1995, 13(1):57-62. |
| [5] | Fan Z L, Zhang Y L, He Z. Preliminary research on numerical simulation of transonic wall interference for aircraft model tests[J]. Acta Aeronautica et Astronautica Sinica, 1997, 18(2):210-214.(in Chinese)范召林, 张玉伦, 贺中. 跨声速飞机模型试验洞壁干扰数值模拟的初步研究[J]. 航空学报, 1997, 18(2):210-214. |
| [6] | Fan Z L, Zhang Y L, He Z, et al. Numerical calculation for three dimensional non-linear transonic wall interference[J]. Acta Aerodynamica Sinica, 1997, 15(2):145-152.(in Chinese)范召林, 张玉伦, 贺中, 等. 跨声速三维非线性洞壁干扰的数值计算[J]. 空气动力学学报, 1997, 15(2):145-152. |
| [7] | Yin L P, He Z, Yu Z S, Fang Z L, Chen Z B. Research on subsonic wall interference correction for model tests at high angle of attack[J]. Experiments and Measurements in Fluid Mechanics, 2000, 14(3):37-41.(in Chinese)尹陆平, 贺中, 于志松, 范召林, 陈作斌. 亚声速大迎角模型试验洞壁干扰修正方法研究[J]. 流体力学实验与测量, 2000, 14(3):37-41. |
| [8] | Allan M R, Badcock K J. A RANS investigation of wind tunnel interference effects on delta wing aerodynamics[R]. AIAA 2003-4214. |
| [9] | Masataka Kohzai, Makoto Ueno. Wall and Support Interference Corrections of NASA Common Research Model Wind Tunnel Tests in JAXA[R]. AIAA 2013-0963. |
| [10] | Maseland J E J, Laban M. Development of CFD-based interference models for DNW-HST transonic wind tunnel[R]. AIAA 2006-3639 |
| [11] | Robert C Griffiths, Kenneth D Visser. Panel code estimates of wind tunnel wall and support interference effects on the HSCT[R]. AIAA 2000-4020. |
| [12] | Alexander J Krynytzky. Parametric model size study of wall interference in the boeing transonic wind tunnel using TRANAIR[R]. AIAA 2004-2310. |
| [13] | Alexander J Krynytzky. Uncertainty evaluation of wall interference in a large transonic wind tunnel[R]. AIAA 2010-4341. |
| [14] | Li Y H, Huang Y, Wang Y Q, et al. Wing-body thickness effects on aerodynamic and vortex flow characteristics of a common low aspect ratio flying-wing configuration at transonic flow[J]. Acta Aerodynamica Sinica 2015, 33(3):302-306.(in Chinese)李永红, 黄勇, 王义庆, 等. 翼身相对厚度对小展弦比飞翼布局跨声速气动特性及流动机理的影响研究[J]. 空气动力学学报, 2015, 33(3):302-306. |
| [15] | Su J C, Huang Y, Li Y H, et al. Support interference of low aspect ratio flying-wing from subsonic to supersonic speed[J]. Acta Aerodynamica Sinica, 2015, 33(3):289-295.(in Chinese)苏继川, 黄勇, 李永红, 等. 小展弦比飞翼亚、跨、超声速支撑干扰研究[J]. 空气动力学学报, 2015, 33(3):289-295. |
| [16] | Su J C, Huang Y, Zhong S D, et al. Research on flow characteristics of low-aspect-ratio flying-wing at transonic speed[J]. Acta Aerodynamica Sinica, 2015, 33(3):307-312.(in Chinese)苏继川, 黄勇, 钟世东, 等. 小展弦比飞翼跨声速典型流动特性研究[J]. 空气动力学学报, 2015, 33(3):307-312. |