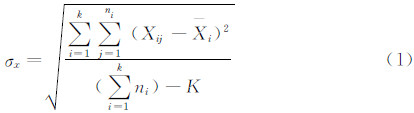0 引言
风洞试验作为航空航天飞行器研制和发展的主要气动力数据来源,其数据质量的好坏是构成飞行器设计风险的重要因素之一。要最大限度地减小与风洞试验有关的风险因素,最经济、有效的手段之一就是开展缩尺模型风洞试验数据与全尺寸飞行数据的相关性研究,而开展风洞与飞行相关性研究首先要对风洞试验基准数据进行提取和数据质量评估[1]。
国内现有的风洞试验技术体系主要是针对常规布局飞机而建立起来的,难以满足以融合体飞翼布局为代表的未来作战飞机气动力关键技术攻关以及设计和研制等方面的要求。为研究飞翼布局模型风洞试验的精准度以及不同风洞试验数据的相关性问题,欧美国家先后推出了多个具有标模意义的通用研究模型,如波音公司设计的UCAV1301/1302/1303飞翼系列、欧洲主导美国参与的NATO RTO AVT-161项目组提出的SACCON通用飞翼研究布局以及NASA提出的65°VFE-2模型[2, 3, 4, 5, 6]。针对此类布局的国内试验手段单一、未成体系,试验数据修正方法也不健全、不统一,还缺乏适用于此类布局的试验数据质量评估标准。因此,迫切需要开展相关的试验技术研究,研究确定具有代表性的融合体飞翼布局外形,建立国内统一的新型布局飞机高、低速风洞试验标模,在主要的生产型风洞中开展系统对比试验和数据相关性研究,分析研究此类新型布局飞机的气动特性和流动机理,建立试验数据精准度评价指标和评估方法,探索和研究提高试验数据质量的有效手段和措施,以尽快建立较完整配套的试验研究体系,为下一代飞行器研制提供技术支撑。为此,由气动中心高速所牵头、联合航空气动院、航天十一院等风洞试验单位联合开展 “小展弦比飞翼风洞试验技术” 攻关项目,以建立小展弦比飞翼标模体系。所建立的高速模型在国内三座1.2m跨、超声速风洞进行了飞翼标模对比实验和精准度研究,以研究飞翼布局模型风洞测力试验的精准度以及不同风洞试验数据的相关性,为以融合体飞翼布局为代表的未来作战飞机气动力试验精度提供参考。
本文介绍飞翼布局的典型流动特性,对比分析了飞翼标模在三座风洞的试验精度,给出了典型马赫数下的测力精度范围,最后对三座风洞试验结果的主要差异进行了分析。
1 模型与试验设备试验模型为翼身融合体的小展弦比飞翼布局全金属模型,支撑方式为尾支撑。小展弦比飞翼标模基本外形参数见图 1,其前缘后掠角为65°,后缘后掠角为±47°,平均气动弦长9.56m,力矩参考点距头部长度为6.9m。试验模型缩比为1 ∶19,模型零迎角时在风洞中的堵塞度约为1%。为保证外形简洁、易于加工,模型由翼身融合体、头部下方盖板和左右航向控制面等部件构成,图 2为飞翼标模尾撑装配图。采用该模型和统一的六分量测力天平和尾支杆在国内三座1.2m跨、超声速风洞中先后进行了小展弦比飞翼标模的对比试验和精准度试验研究,这些风洞包括气动中心高速所FL-24风洞、航空气动院FL-2风洞和航天十一院FD-12风洞。图 3为标模在风洞中的安装照片。为研究不同风洞数据相关性,高速风洞试验根据不同风洞试验的特点和具体情况,设计加工各自的过渡接头使模型处于风洞流场的均匀区;根据统一制定的高速试验大纲和数据处理大纲在不同风洞进行测力试验,试验采用固定马赫数和侧滑角、改变迎角的常规方式进行。鉴于不同风洞动态品质、噪音水平的差异会影响到转捩雷诺数,为保证不同风洞试验数据的相关性和可比性,在试验中采用了人工转捩方式进行风洞试验。转捩带粘贴位置统一在距机翼前缘5%当地弦长处,采用高度为0.12mm的柱状转捩带。
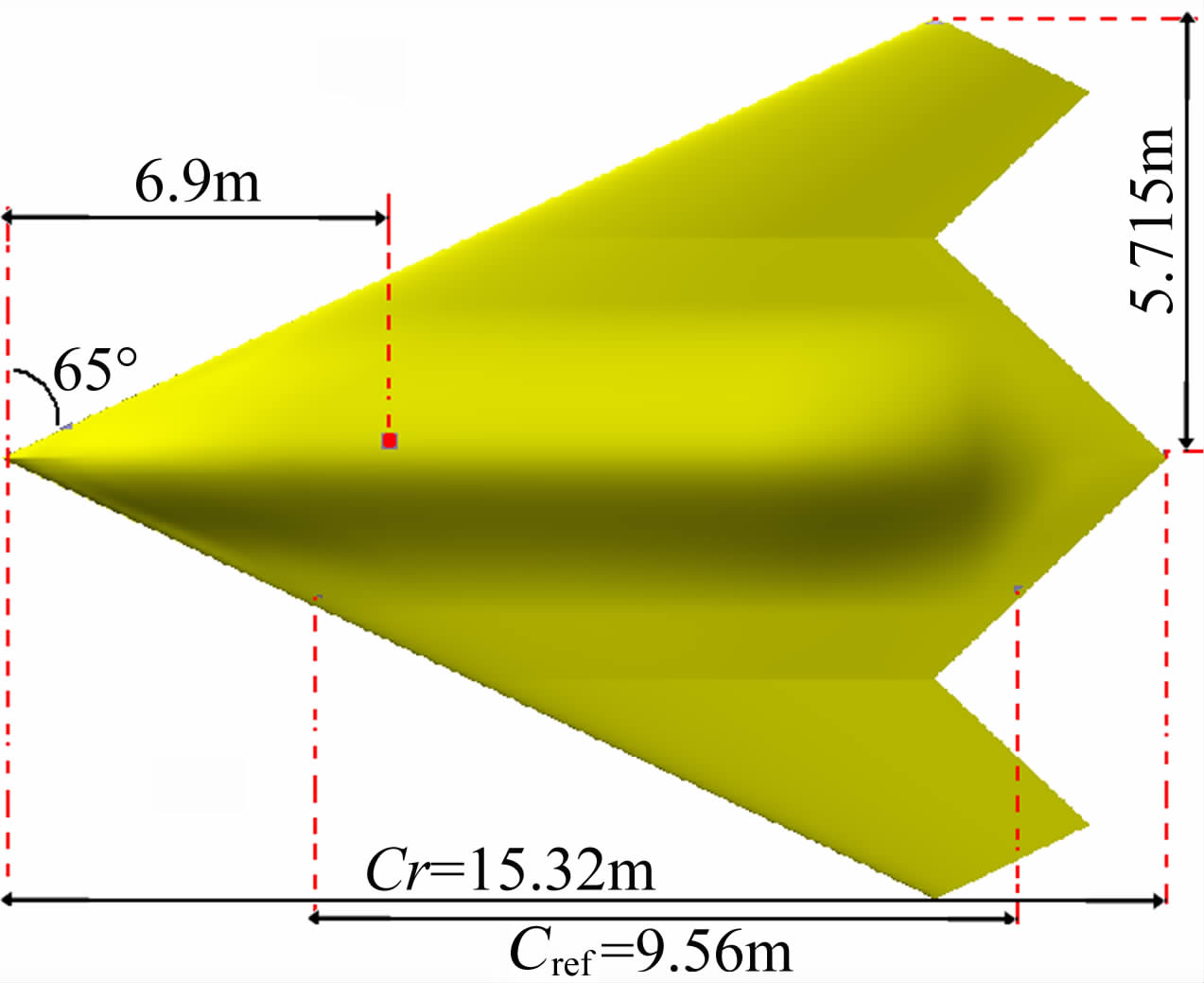 |
| 图 1 小展弦比飞翼标模模型示意图Fig. 1 Basic geometry parameters of the model |
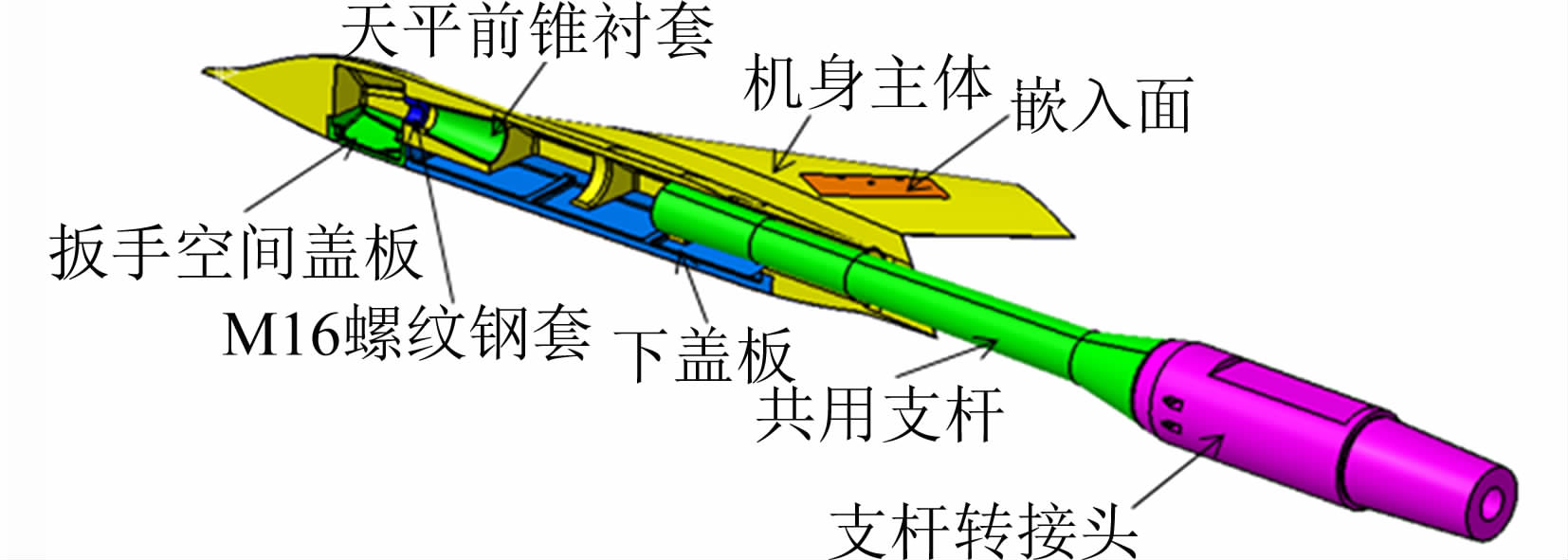 |
| 图 2 小展弦比飞翼标模尾撑装配图Fig. 2 Assemble photo of the model with tail support |
 |
| 图 3 小展弦比飞翼标模在风洞中的安装照片Fig. 3 Picture of the model in the wind tunnel |
大量研究结果表明对于飞翼布局飞行器,在跨声速条件下存在三个典型的流动状态[7, 8, 9, 10, 11, 12, 13, 14],即:在小迎角范围飞翼布局上翼面以附着流为主;随着迎角的增大,在上翼面会形成一对稳定的前缘涡,使飞翼布局升力特性呈现非线性;当迎角达到某临界值时,翼面上方的前缘涡涡核内的轴向速度会突然降低,以至形成驻点,其后的一个有限区域内是回流状态,即所谓的前缘涡破裂,前缘涡的破裂使飞翼布局升力线斜率降低。图 4是典型马赫数下飞翼标模纵向气动力系数在FL-24风洞中的试验结果,该结果进行了模型自重、天平弹性角和气流偏角修正,且后文的不同风洞对比试验数据都是进行此修正后的数据。可以看出,跨声速范围,在小迎角时,全机为附着流动,升力系数和俯仰力矩系数随迎角线性变化,纵向静稳定;在中等迎角,机翼前缘涡出现并不断发展,使全机升力线斜率和俯仰力矩曲线斜率增大,焦点后移;随着迎角的继续增大,前缘涡破裂(M=0.8,涡破裂迎角在12°附近),使全机升力线斜率和俯仰力矩曲线斜率减小,同时,在前缘涡破裂初始迎角附近,升力线斜率大幅减小,俯仰力矩出现上仰。超声速时,其气动力随迎角的变化规律受前缘涡流动的影响较小,与常规布局基本相同。飞翼布局的这种气动特性对不同风洞的测力试验精度和数据相关性具有直接的影响,这点将在后文进行详细阐述。
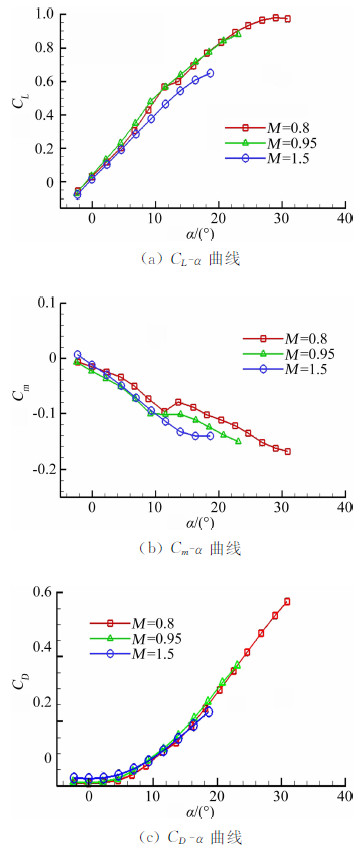 |
| 图 4 典型马赫数下纵向气动力系数随迎角的变化曲线Fig. 4 Aerodynamic coefficients versus angle of attack at typical Mach numbers |
试验精度是通过求取同一风洞七次重复性试验结果的样本标准偏差获得的。首先对典型马赫数下飞翼标模在三座风洞同期测力试验精度随模型迎角的变化进行对比分析,试验结果如图 5所示。
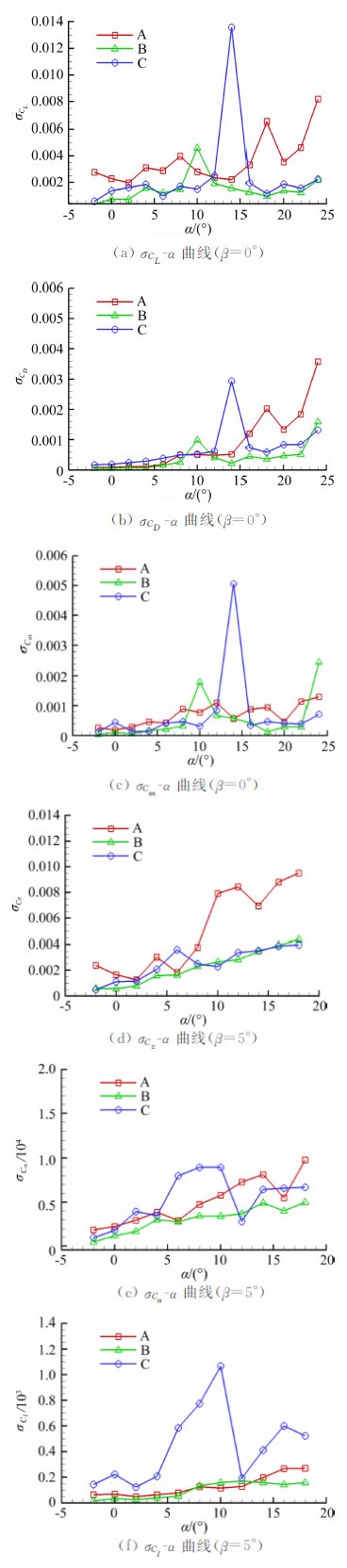 |
| 图 5 三座风洞精度指标对比Fig. 5 Comparisons of test precision of the model in the three wind tunnels |
实验结果表明,在飞翼标模模型和天平相同的情况下,不同风洞的试验精度存在一定的差异,升力系数在B、C风洞中试验误差的分布较为集中,A风洞的试验误差整体较B、C风洞略大。在小迎角范围(此时飞翼标模背风面主要是附着流为主),阻力系数和俯仰力矩系数在三座风洞的误差均较小,且分布较为集中,但随着迎角的增大,飞翼标模背风面由附着流状态变为以前缘涡流动为主,阻力系数和俯仰力矩系数试验误差变大,且散布变大,特别是阻力系数,A风洞的试验误差在前缘涡破裂之后(α>12°)迅速变大,B、C风洞在前缘涡破裂之后的试验精度较为接近,这可能是由不同风洞的流场品质、模型振动等原因造成的。横向气动力系数在三座风洞中的试验误差均随迎角的增大有不同程度的增加,但整体误差较小,且量值基本相当。
以上是单点(各个迎角)七次重复的标准差分析,为与基于歼七标模制定的高速风洞测力实验精度指标进行对比,根据均方根误差公式(1)对迎角-2°~4°区间范围的整体精度进行了计算。
计算结果如表 1和表 2所示。表 1列出了马赫数为0. 8时飞翼标模气动力系数三座风洞测力试验精度的比较,表 2给出了典型马赫数下标模在三座风洞中的试验精度范围。
| 风洞 | σ C L | σ C m | σ C D | σ C l | σ C Y | σ C n |
| A | 2.60E-03 | 3.00E-04 | 1.32E-04 | 5.69E-05 | 3.26E-04 | 4.28E-05 |
| B | 1.10E-03 | 1.00E-04 | 9.37E-05 | 5.08E-05 | 7.68E-05 | 1.95E-05 |
| C | 1.20E-03 | 3.00E-04 | 2.87E-04 | 2.01E-04 | 1.90E-04 | 5.99E-05 |
| 马赫数 | β=0° | β=5° | ||||
| σ C L | σ C m | σ C D | σ C l | σ C Y | σ C n | |
| 0.8 | 1.1E-03~2.6E-03 | 1.0E-04~3.0E-04 | 9.5E-05~2.87E-04 | 5.1E-05~2.00E-04 | 7.68E-05~3.26E-04 | 1.9E-05~6.0E-05 |
| 0.95 | 1.1E-03~2.4E-03 | 3.0E-04~7.0E-04 | 9.6E-05~2.66E-04 | 4.5E-05~2.00E-04 | 1.20E-04~2.60E-04 | 3.0E-05~5.9E-05 |
| 1.5 | 9.0E-04~1.3E-03 | 1.9E-04~2.0E-04 | 4.5E-05~7.9E-05 | 2.0E-05~1.40E-04 | 6.40E-05~1.20E-04 | 1.5E-05~3.5E-05 |
从表 1中可以看出,B风洞的测力精度明显高于A风洞和C风洞,在M=0.8时,B风洞测力试验精度全部达到国军标合格指标,并且俯仰力矩、阻力、滚转力矩和偏航力矩系数达到了国军标先进指标。C风洞测量的气动力系数也全部达到国军标合格指标,部分达到先进指标。A风洞升力系数的测量精度较差,未达到合格指标要求。从表 2中可以看出,超声速时飞翼标模在三座风洞的测力精度均较高,散布较为集中,均达到国军标合格指标,并且超过50%的测量值达到国军标先进指标。由前文针对飞翼标模跨声速流动特性的研究结果表明[15, 16, 17]:跨声速时由于其复杂的分离和激波/前缘涡干扰特性,相对于以附着流为主的传统布局,气动特性对流动特性比较敏感,试验测值存在一个散布带,此散布带的出现使得测力精度较差,不同风洞数据的相关性也较差,但总体来说在小迎角附着流状态,三座风洞的数据相关性较好,测力精度满足基于标模制定的高速风洞测力实验精度指标要求。
2.3 三座风洞试验数据对比分析在确定风洞试验总体方案时采取了多项技术措施包括底阻、模型自重、弹性角、气流偏角等参数的修正,以确保不同风洞试验结果的可对比性。图 6给出了M=0.8时三座风洞基本纵向试验结果的对比,可以看出,在涡破裂之前不同风洞的纵向气动力试验值比较一致,但在涡破裂后不同风洞的试验值存在一定的差异,其中A和C风洞所得的涡破裂迎角较为一致,并且在涡破裂后的试验值一致性仍然较好,而B风洞的涡破裂迎角较A和C风洞提前约2°,并且在涡破裂后气动力试验值与A和C风洞相差较大。在模型、天平和支杆相同的情况下,三座风洞在涡破裂后气动力试验值的这种差异主要是风洞洞体结构形式、支撑系统以及湍流度等差异引起的,总的来说A风洞和C风洞的洞壁开孔形式一致,均为上、下开孔(直孔),左、右实壁,而B风洞为四壁开孔(斜孔),A风洞和C风洞的支撑系统距模型头部的距离也较B风洞更远。因此,风洞的结构形式、支撑系统以及湍流度对飞翼布局涡破裂起始迎角和涡破裂后的气动特性影响较大。
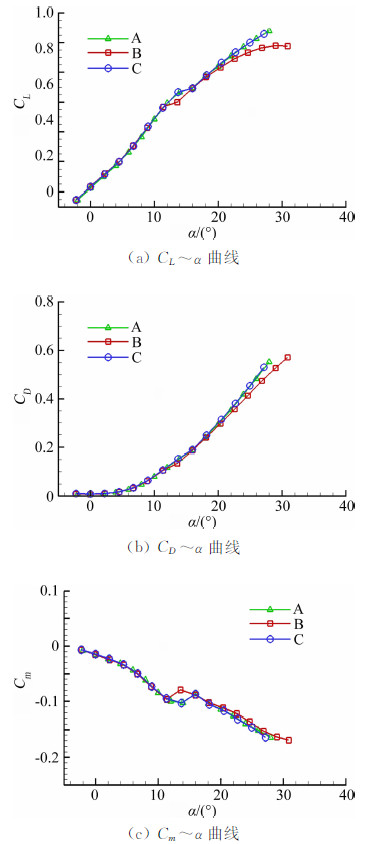 |
| 图 6 M=0.8, β=0°时三座风洞基本纵向试验结果的对比Fig. 6 Comparison of experimental data at M=0.8, β=0° |
图 7给出了三座风洞气动力导系数随马赫数的变化。从图 7(a)可以看出M=0.6、0.8、0.9时三座风洞所测零升阻力系数相差在0.0010之内,M=0.95最大相差0.0013,M=1.0、1.05、1.1、1.2,相差在0.002~0.005,差异明显较大,跨声速阶段这种较大差异与风洞消波特性有较大关系。三座风洞的升力线斜率(-2°~2°范围)差异较小,最大差异为0.002。各风洞所测模型的零升迎角差异略大,散布带约为0.2°,总体看B风洞和C风洞比较接近,A风洞零升迎角在马赫数0.6至1.5范围较B风洞和C风洞偏大0.07°~0.3°。零升俯仰力矩系数和俯仰力矩随迎角的斜率三座风洞的试验值相关性较好。
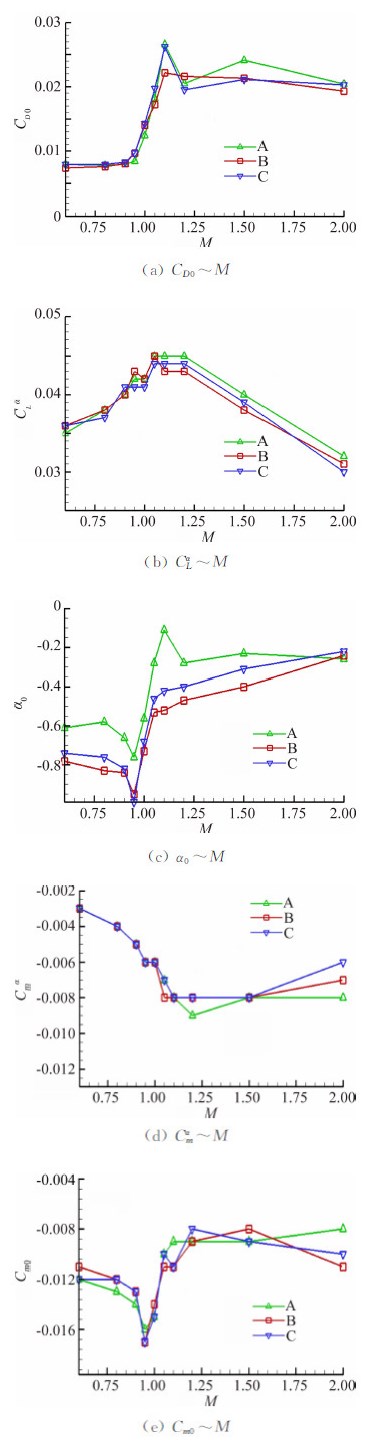 |
| 图 7 三座风洞气动力(导)系数随马赫数的变化Fig. 7 Aerodynamic derivatives versus Mach number |
通过对小展弦比飞翼标模在三座风洞的测力试验结果和试验精度的对比分析,定量地研究了不同风洞的数据相关性,得出以下结论:
(1) 小展弦比飞翼标模风洞测力试验精度及不同风洞数据相关性与飞翼布局流动特性关系较大,在小迎角附着流状态,不同风洞的数据相关性较好,测力精度较高,涡破裂后不同风洞的数据相关性和试验精度都有不同程度的降低;
(2) 跨声速条件下由于飞翼布局背风面复杂的流动特性,使得其试验精度较超声速略差。
(3) 不同风洞数据相关性整体较好,差异主要体现在升力特性拐点起始迎角、近声速附近马赫数的零升阻力系数和零升迎角,后续将对引起此差异的影响因素,如洞壁干扰、远场支撑系统干扰等进行深入研究。
| [1] | Huang Yong, Dong Lixin, Zhao Kecheng, et al. On the correlation of force test results of a tactical missile calibration model in five different wind tunnels[J]. Experiments and Measurements in Fluid Mechanics, 2002, 16(2):16-20.(in Chinese)黄勇, 董立新, 赵克诚, 等. 战术导弹标模五座风洞试验数据的相关性研究[J]. 流体力学试验与测量, 2002, 16(2):16-20. |
| [2] | Wyatt E C, Hirschberg M J. Transforming the future battlefield:the DARPA/air force unmanned combat air vehicle(UCAV) program[R]. AIAA 2003-2616. |
| [3] | Liersch C M, Huber K C. Conceptual design and aerodynamic analyses of a generic UCAV configuration[R]. AIAA 2014-2001. |
| [4] | Collie W V, Burgun R, Heinzen S N. Advanced propulsion system design and integration for a turbojet powered unmanned aerial vehicle. AIAA 2003-415. |
| [5] | Sukumar Chakravarthy, David Chi, Uri Goldberg. Flow prediction around the SACCON configuration using CFD++[R]. AIAA 2010-4563. |
| [6] | Woolvin S J. A conceptual design study of the 1303 UCAV configuration[R]. AIAA 2006-2991. |
| [7] | Fritz W. Numerical simulation of the peculiar subsonic flow-field about the VFE-2 delta-wing with rounded leading-edge[R]. AIAA 2008-0393. |
| [8] | Wang Guangxue, Deng Xiaogang, Liu Huayong, et al. Application of high-order scheme(WCNS) at high angles of incidence for delta wing[J]. Acta Aerodynamica Sinica, 2012, 30(1):28-33.(in Chinese)王光学, 邓小刚, 刘化勇, 等. 高阶精度格式WCNS在三角翼大攻角模拟中的应用研究[J]. 空气动力学学报, 2012, 30(1):28-33. |
| [9] | Wang Yuntao, Zhang Yulun, Wang Guangxue, et al. Numerical study on flow structure over a delta wing[J]. Acta Aerodynamica Sinica, 2013, 31(5):554-558.(in Chinese)王运涛, 张玉伦, 王光学, 等. 三角翼布局气动特性及流动机理研究[J]. 空气动力学学报, 2013, 31(5):554-558. |
| [10] | Wang Guangxue, Deng Xiaogang, Wang Yuntao, et al. High-order numerical simulation of vortex breakdown on delta wing[J]. Chinese Journal of Computational Physics, 2012, 29(4):489-494.(in Chinese)王光学, 邓小刚, 王运涛, 等. 三角翼涡破裂的高精度数值模拟[J]. 计算物理, 2012, 29(4):489-494. |
| [11] | Chu J, Luckring J M. Experimental surface pressure data obtained on 65° delta wing across Reynolds number and Mach number ranges[R]. NASA TM-4645, 1996. |
| [12] | Jobe C E. Vortex breakdown location over 65 Deg delta wings empiricism and experiment[J]. Aeronautical Journal, 2004, 108(1087):475-482. |
| [13] | Schiavetta L A. Shock effects in delta wing vortex breakdown[J]. Journal of aircraft, 2009, 46(3):903-914. |
| [14] | Donohoe S R, Bannink W J. Surface reflective visualisations of shock-wave/vortex interactions above a delta wing[J]. AIAA Journal, 1997, 35(10):1568-1573. |
| [15] | Li Y H, Huang Y, Wang Y Q, et al. Wing-body thickness effects on aerodynamic and vortex flow characteristics of a common low aspect ratio flying-wing configuration at transonic flow[J]. Acta Aerodynamica Sinica, 2015, 33(3):302-306.(in Chinese)李永红, 黄勇, 王义庆, 等. 翼身相对厚度对小展弦比飞翼布局跨声速气动特性及流动机理的影响研究[J]. 空气动力学学报, 2015, 33(3):302-306. |
| [16] | Su J C, Huang Y, Li Y H, et al. Support interference of low aspect ratio flying-wing from subsonic to supersonic speed[J]. Acta Aerodynamica Sinica, 2015, 33(3):289-295.(in Chinese)苏继川, 黄勇, 李永红, 等. 小展弦比飞翼亚、跨、超声速支撑干扰研究[J]. 空气动力学学报, 2015, 33(3):289-295. |
| [17] | Su J C, Huang Y, Zhong S D, et al. Research on flow characteristics of low-aspect-ratio flying-wing at transonic speed[J]. Acta Aerodynamica Sinica, 2015, 33(3):307-312.(in Chinese)苏继川, 黄勇, 钟世东, 等. 小展弦比飞翼跨声速典型流动特性研究[J]. 空气动力学学报, 2015, 33(3):307-312. |