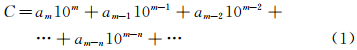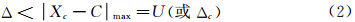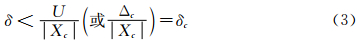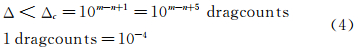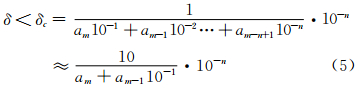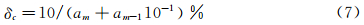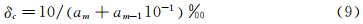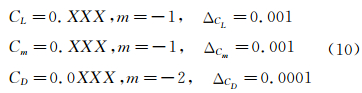0 引 言
空气动力学中流动物理方程建模的研究，方程求解高阶算法的发展，网格生成技术的进步，超大规模计算机的迅速出现及并行算法的研究，再加上实验设备的发展和测试技术的提高，使得航空航天等工程设计者尽管在不同设计阶段需要的气动数据精度可以不同，但为了提高飞行器的性能，扩大飞行走廊[1]，总要求气动工作者所提供的CFD和实验数据是高精度保真的。这就提出如下问题：
1)高精度保真的指标是什么？给出的数值结果达到什么程度就是高精度保真了？能否给出一个哪怕是大致的指标？
2)怎样才能做到高精度，至少以下工作要做好：①计算出发的物理方程要准确，层流的方程为NS方程是准确的，但对于湍流还要寻求精确的描述；②气动算法应该高精度；③计算用的网格、算法和物理模型要匹配。
3)怎样判定结果已达到了高精度。通过实验验证是一种方法，但存在实验结果必须先证明是高精度的问题，能否另找一种方法实现这种验证呢？
本文讨论这些问题。
1 高精度的指标当飞行器外形给定，飞行器的气动力、热等任一物理量的值就确定了(我们称它为真值，虽然它是不知道的)。设其值可表达为：
当用CFD进行计算时，我们可给出近似值Xc，假设计算值和真值相比，它们前n位有效数值准确。那么计算值的绝对误差的最大值是：
相对误差是：
进一步可以给出：
例如，当n=2，前两位真值准确
当n=3，前三位真值准确
现有的二阶精度的计算结果，气动压力有的可达n=2两位真值准确。气动热还远达不到n=2真值准确。我请教过多位设计师，问他们准确到多少位就满意了，他们为难地说在实际工程中有三位真值准确就行了。例如运输机，一般升力系数CL、力矩系数Cm和阻力系数CD要求三位真值准确，可以要求：
这种情况启示我们所谓高准确的CFD计算结果，可首先定为达到三位有效数据真值准确作为大致的指标。
2 湍流LES、DNS求解问题要进行保真的高精度计算，首先要解决流动方程的正确描述。湍流就是一个重要问题。湍流的计算有模式理论、大涡模拟(LES)和直接数值模拟(DNS)三种。
2.1 湍流的模式理论及LES关于湍流计算对模式理论有以下共识：
1) 以雷诺应力方程为基础，采用一方程模型、k-ε和k-ω等RANS模式理论[2, 3, 4]，可给出不复杂外形和不大分离区(这多属于平衡湍流)的压力分布、摩阻、力矩及热流分布。压力的计算精度高些，但摩阻、力矩和热流的计算精度尚需进一步改进。
2) 为了能计算复杂外形和大分离区的非平衡流动，诸多文献建议采用LES方法，但应较好地计算亚格子网格应力，特别近壁面区的模型。有人建议壁面附近用RANS、外部区域用LES的混合RANS-LES的方法[5]。
但是，我们认为，对LES，除了壁面区的模型外，还应研究以下问题：
1) LES原是建立在空间滤波基础上的，其流动与时间有关。RANS是建立在时间平均基础上的，不同体系的RANS和LES能统一起来吗？两者之间的连接有通用的方法吗？要寻求RANS-LES统一的支持理论，不然就限于经验的范围。
2) 对于湍流，实验证明在高马赫数下，可能存在小激波，此时LES的模型还适用吗？
3) 数值求解LES方程时，大规模并行计算(HPC)出现问题。设特征空间为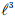
，划分计算网格，此时小网格尺度为:
这里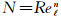
为LES的计算网格数，式中
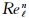是用来流条件和特征长度
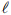计算，Chapman[6]认为n=1.8,Choi和Moin[7]认为n=13/7=1.875。
当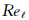
=105时，尺度为Δ的网格点为109，即10亿。如果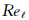=107，需上万亿网格点。最近日本人用他们国家最快的计算机(10 PF/S，我国天河计算机为50 PF/S)，用LES数值求解了汽车绕流，网格数达数万亿。如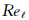=108，需数万万亿网格点。工程上的 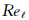高达109。这就表明，没有HPC，求解LES是困难的,还存在结果如何平均的问题。有了HPC，甚至有更高的运算速度，要解决工程上高雷诺数的问题，2030年前恐怕也是困难的。因此应从物理机理的角度发展简化的LES模式理论或其他方法。
一般认为，NS方程是湍流的物理方程。对于特征空间为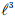，当雷诺数为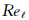时，为保证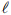能包含大涡，Δ可能小至Kolmogorov以下尺度。计算网格点数至少应该为
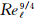，网格点间距为Δ ，也可写成：
对于上面的分析，n=9/4，这是Chapman的估计，Choi和Moin指出n=37/14。 这里的指数n比LES的大很多，要对NS方程求解，网格点数比LES密很多。如Re=107，对LES为4×1012,对DNS为5.6×1015。这样小的尺度要求，在现有的超大规模计算机上是可以划分的，甚至可划分的更小。但是按照NS方程是连续流的条件，根据连续流的要求应有λ/Δ<Kn=10-2，这里λ为分子碰撞自由程，对空气它随空间高度增加，在地面取最小值，约为6.68×10-8m，于是要求Δ>100λ。此时按规定划分网格，就落入了滑流的范围，流动的计算就进入了另一领域。
但是，必须指出，DNS求解能提供非常丰富的湍流特征。它能帮助我们验证模式理论，帮助我们验证LES方法和RANS-LES方法，可以启示我们发展更新湍流结论的认识，发展更新的湍流描述方法。
2.3 从连续流到稀薄气体流应发展Boltzmann算法流体力学的发展，先是无黏性流Euler方程求解，进一步发展到NS方程求解，下一步自然也就是Boltzmann方程求解。这个问题早已经提出。最近，周恒和张涵信在文献指出，在研究近空间高超声速滑翔机动飞行时，流场内可能同时出现连续流、不连续流的情况，此时也需要研究Boltzmann方程,才能正确给出所需的物理量。再加上DNS巨型网格算法出现的物理问题，证明这一趋势是正确的。但这里Boltzmann算法的发展，应该考虑高温化学反应等效应。目前采用的诸如Shekhov类型的BGK方法，仅是对碰撞积分的简化考虑，这里仍存在碰撞积分的模型问题，应发展全面反应碰撞积分的方法。
3 高阶计算方法及网格、边界、模型的协调匹配问题在建立保真的流动物理模型后,采用高精度格式是必要的。现已有有限差分和有限体积、紧致差分以及滤波等各类[9, 10, 11]高精度的差分方法。高精度自适应的非结构网格高精度算法可参见王志坚主编的书[9]。
现在讨论差分计算方面的情况。在美国，Harten和Osher等提出了ENO格式(1987，1988)，它是非线性插值方法,能抑制激波处的波动。在中国，张涵信、贺国宏、陈坚强、李沁等提出用熵增条件抑制激波波动的ENN方法(1994)。傅德薰、马延文等提出抑制激波波动的群速度法，还可用于紧致差分上(1994)。沈孟育研究广义紧致格式时，以三阶格式为例，证明独立发展的ENO、熵增条件和群速度三种抑制激波波动的方法所得到的表达式是一致的(1995)。邓小刚(1996)在Lele高阶线性节点和半节点紧致格式基础上，采用原始变量插值法构造了新颖的CNS高阶紧致格式。因用了类似ENO的关系，激波附近无波动。再后，加权无波动格式WENO(1994)提出后，上述格式又引入了加权分析，如WENN(1998)和WCNS(1998，2000)。这些研究成果，在验证典型激波或其他典型简单绕流上都能很好地给出计算结果。但对于航天、航空飞行器的计算，只有个别的结果，无法给出摩阻和热流的满意的计算结果。特别对于高马赫数流动，再加上湍流方程尚有问题，要建立通用的高阶格式的平台需再加努力。
但这节我们要强调重视网格、模型和计算格式协调匹配问题。因涉及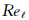及边界的影响，需要求解物理量的导数，这会损坏计算精度。更主要的是涉及计算格式与网格和模型的匹配。设三个无量纲坐标方向计算网格的尺度为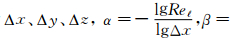
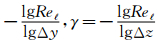，m为计算格式的名义精度(或称无粘性部分计算的精度)，只有当m>>max(α,β,γ) 时，真正的粘性流的计算精度才是高的。上面关于LES的计算，无量纲的网格尺度为：
只有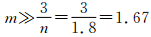
时，真实计算精度才是高的。看来，3阶、4阶精度恐怕还是不够的。
如果流动的物理方程已知，计算网格和高阶计算格式给定，那么CFD的计算结果是否达到了所要求的精度？如何验证、确认？流动方程的理论解一般给不出，用这条道路无法判定。另一方法，例如，美国组织召开的系列DPW(Drag Predictions Workshop)研讨会[12]，利用和计算相同的外形、边界条件等做实验，用实验结果和计算值比较，但这存在实验值是否准确，因为测量技术不能保证非常准确。我认为可以尝试利用大数据系统的概率统计理论，即对同一问题，用不同网格、不同精度格式做计算，然后对关心的物理量利用大数定律求其数学期望和方差，根据其期望和方差进一步给出修正的数学期望的估值。这一方法我们已经做了初步应用[13]，得到了好的结果。文献[14]给出了第二次DPM会议的结果，它是众多研究机构利用各自的CFD软件、不同的算法和网格，围绕DLR-F6外形(不带发动机短舱)进行了大量计算。以M∞=0.75，Rec=3×106，CL=0.5这一状态为例，我们对第二届DPW的全部计算数据进行了分析。按我们前述的方法，三位准确的真值CD=0.029406，而精细的实验作比较的结果为CD=0.0295。
5 结 论综上所述，有以下结论：
(1) 什么是保真的高精度数据?这里提出三位有效数据真值准确是否可暂作一个标准。
(2) LES和RANS的结合是一个现今认为最好的模式理论，但作湍流的通用模型还有进一步发展的空间。在实际高Re情况下，即使用HPC计算，未来几十年内也难以用LES解决实际工程问题。NS方程可用作湍流的基本方程，可用HPC计算，但在Re很大时，要求的网格出现稀薄气体流动，这又出现了新问题。
(3) 发展高阶计算方法是必要的,但必须重视网格问题。网格、边界处理和算法要协调匹配。这里仅讨论了算法精度方法的问题。因流动方程中存在Re数，用高阶格式计算时，对无粘性部分为m阶精度，但粘性部分格式精度会变低。本文提出 m-max(α,β,γ)>>1 作为粘性部分的精度，式中
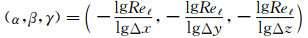
(4) 除用实验结果验证确认CFD计算值外，本文提出对同一问题，用不同格式、不同网格做大量计算，然后利用大数定律理论求其数学期望的方法作为验证、确认方法。
致谢: 本文曾多次与张树海、张来平、李沁和叶友达进行了讨论，他们提出了很好的建议，作为八十岁的我在此表示感谢。
| [1] | Tinoco E N, Bogue D R, Kao T J, et al. Progress toward CFD for full flight envelope[J]. The Aeronautical Journal, 2005, 109:451-460. |
| [2] | Spalart P R, Allmaras S R. A one-equation turbulence model for aerodynamic flows[J]. La Recherche Aerospatiale, 1994, 1:5-21. |
| [3] | Menter F. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32:1598-1605. |
| [4] | Wilcox D C. Turbulence modeling for CFD, DCW Industries[M]. 3rd edition, November 2006. |
| [5] | Direct and large-eddy simulation 9(DLES 9). ERCOFTAC workshop, April 3-9, 2013, Dresden, Germany,Http://www.dles9.org. |
| [6] | Chapman D R. Computational aerodynamics development and outlook[J]. AIAA J., 1979, 17:1293. |
| [7] | Choi H, Moin P. Grid-point requirements for large eddy simulation:chapman's estimates revisited[J]. Phys. Fluids, 2012, 24:011702. |
| [8] | 周恒, 张涵信. 空气动力学的新问题[J]. 中国科学, 物理学, 力学, 天文学. 2015, 45:104789. |
| [9] | Wang Z J. Adaptive high order methods in computational fluid dynamics[M]. Vol.2, Advances in Computational Fluid Dynamics, World Scientific. |
| [10] | Zhang H X, et al. Some recent progress of high-order methods on structured and unstructured grids in CARDC[C]//Invited Lecture, ICCFD8, July 14-18, 2014, Chengdu, China. |
| [11] | Deng X G. Developing high-order linear and nonlinear schemes satisfying geometric conservation law[C]//Invited Lecture, ICCFD8, July 14-18, 2014, Chengdu, China. |
| [12] | AIAA applied aerodynamics technical committee[C]//Drag Prediction Workshop. 19th APA Conference, Anaheim, CA 2001. |
| [13] | Kelly R. Laflin, Olaf Bradevsen, Mark Rakowitz, John C Vassberg, Edward N. Tinoco, Richard A. Wahls, Joseph H. Morrison, Jean Luc Godard. Summary of data from the second AIAA CFD drag prediction workshop(Ivited)[R]. AIAA 2004-0555, 42nd AIAA Aerospace Sviences Meeting and Exhibit 5-8, January 2004, Reno, Nevada. |
| [14] | 张涵信, 查俊. 关于CFD验证确认中的不确定度和真值估算[J]. 空气动力学学报, 2010, 28(1):39-45. |