2. 中国白城兵器试验中心, 吉林白城 137001
2. China Baicheng Weapon Test Centre, Baicheng 137001, China
0引言
随着新型可成像式雷达的陆续装备,传统的点源式干扰弹越来越满足不了作战要求,面源式红外干扰弹作为一种新型的红外干扰系统应运而生。如美国MJU 50B红外干扰弹[1],它采用自燃材料,从发射筒到点火前完全封闭,未氧化金属薄片从圆筒中弹出后与空气接触逐渐氧化并辐射热量。薄片的散布规律直接影响了干扰弹的作战效果。
目前研究薄片云团的运动多采用建立诱饵弹整体质点运动模型,认为诱饵薄片为空间均匀球状分布[2]或者采用正态随机数方法[3]获得云团分布。陈乃光[4]建立了低速下薄片的质点模型,忽略了薄片分离过程中相互间气动干扰,得出了自燃薄片的分离散布规律,但是薄片尺寸较大,受气动作用明显,并不适合颗粒质点模型。黄蓓[4]建立了ALE有限体积法下的三维不可压缩方程,耦合刚体运动方程数值模拟了薄片的低速下的静态抛撒过程,并与试验结果做了对比,其研究都仅限于静态低速下的抛撒过程。但是在实战中,干扰弹都是在战机飞行过程中发射。为研究这种干扰弹在动态抛撒过程中薄片初始分离的形态,并解释试验中发现的薄片初始分离过程中头尾次序分离的现象,本文基于刚体动力学理论和碰撞检测、响应模型,耦合流体计算方法对高速运动下集束薄片的分离过程进行了仿真分析。
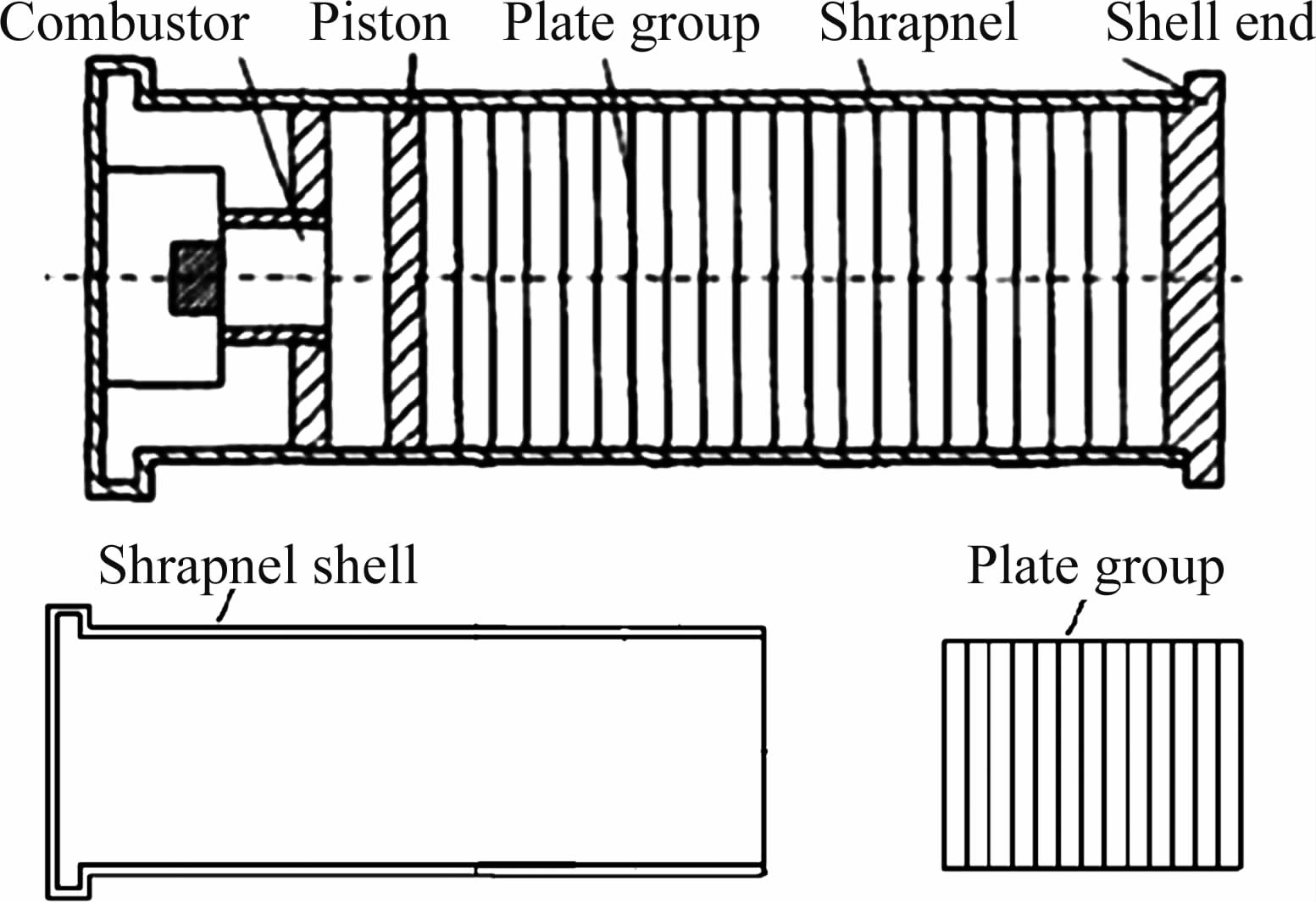
1 数值模拟方法 1.1 薄片动态抛撒过程描述图 1为面源式干扰弹工作示意图。大数量圆柱状薄片摞齐装填,薄片在发射时成串射出,快速散开燃烧形成干扰云团。这个过程中薄片云团的散布形态与散布面积是干扰弹能否产生有效干扰的关键之一,所以研究薄片集束在战机飞行过程中发射的薄片散开机理也是指导其改进设计的重要理论依据。
|
| 图 1 面源式干扰弹工作示意图 Fig. 1 Structure diagram of surfacetype infrared decoy |
建立ALE有限体积法描述下的三维可压缩方程 [5],其积分表达式为:
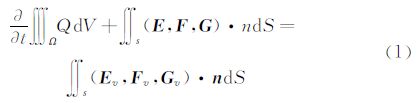

湍流模型采用双方程Realizable k-ε模型 [5],此模型对于不同雷诺数下的边界层流动和带有分离的流动等均有较好的适应性。引入Reynolds平均法得到时均化的流动控制方程,将Reynolds应力表示为湍流粘性系数的函数,湍流粘性系数由湍动能 k 和湍流耗散率 ε 求得。对于近壁区域低雷诺数流动情况,采用壁面函数法进行修正求解。
对控制方程及湍流方程用二阶迎风格式进行空间离散,时间离散采用隐式方案。薄片采用固壁边界,外流场区域来流采用自由来流边界,出流边界由内场外推处理,并根据湍动强度和特征长度来估算入口边界处的 k和ε 值。
采用弹簧近似法和局部网格重构相结合的非结构动网格技术实现分离过程中物体边界运动后流体计算网格的更新 [6]。耦合刚体六自由度运动方程计算获得边界位移量 [7, 8, 9, 10, 11, 12]。
1.3 刚体运动耦合计算方法与碰撞判定方法薄片在空气中的运动过程中主要受气动力作用和薄片间的接触碰撞作用影响。本文碰撞判定定义为薄片之间的间距小于警戒距离时为碰撞作用。薄片间的碰撞定义为刚体的完全弹性碰撞,只有薄片的速度和角速度在碰撞后发生改变。
1.3.1 刚体碰撞检测模型薄片在分离初始位置时间距较小,分离过程中薄片的运动差异性会使其在分离过程中的碰撞频率非 常高。为有效减小数据计算量,提高检测速度,把 薄片间的碰撞判定分为两个步骤:
(1) 预判定。运用球体碰撞模型,以包裹薄片的最小球体为单元,若两球体质心间距离大于其半径和,即 o 1- o 2 ≤r1+r2,判定为薄片未碰撞;若两球体质心间距离小于等于其半径和,即 o 1- o 2 ≤(r1+r2),则进入第二步判定。
(2) 精确判定。通过搜索两薄片表面网格的质心,寻找两薄片间的最近距离,在联系薄片间的相对速度、计算时间步长等参数建立起碰撞条件为:
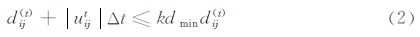
薄片的碰撞模型采用三维刚体碰撞模型,其基本假设如下:
(1) 碰撞薄片均为刚体,碰撞前后薄片无变形,能量无损失;
(2) 碰撞瞬间完成,薄片无相对滑动;
(3) 碰撞瞬间,薄片间撞击应力远大于气动力,不考虑碰撞时气动力的影响。
(4) 碰撞过程中不考虑多体间的碰撞,多体碰撞简化为两两相碰。
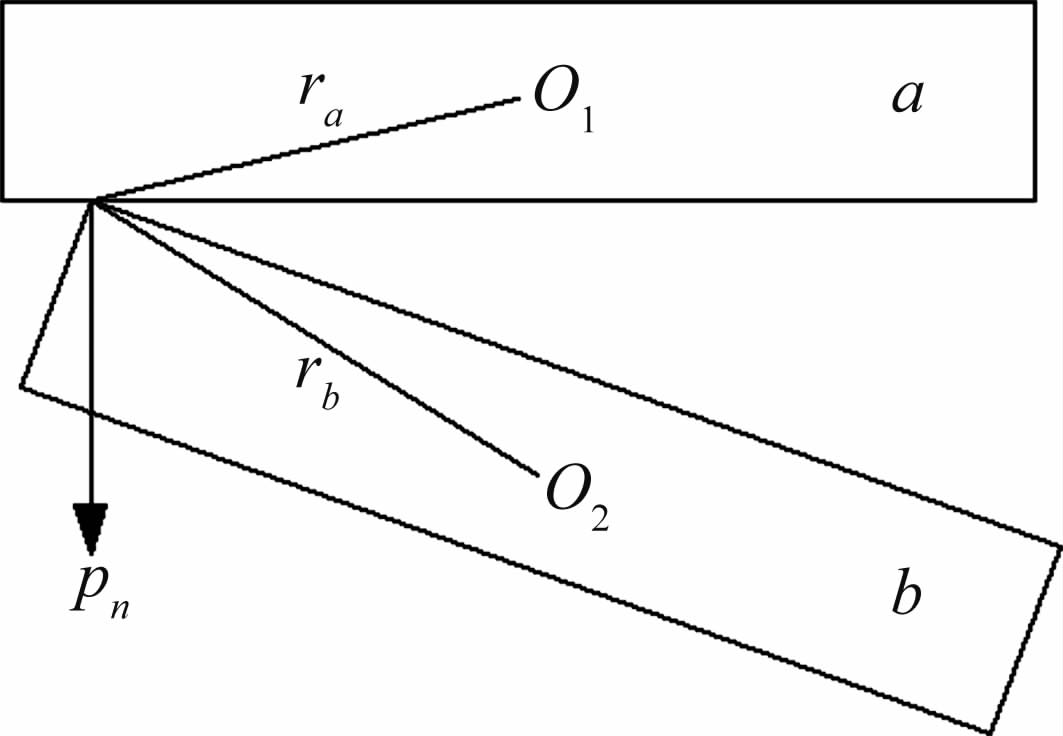
碰撞模型如图 2所示。假设两个薄片 a和b ,质量分别为 ma和mb ,碰撞前 a、b 的质心速度分别为 v a0和 v b0,其体坐标系下的角速度分别为 ω′a、 ω′b,其质心到碰点的距离分别为ra、rb。 坐标系转换张量为 I,则a、b 在碰撞前瞬间碰点的速度为:
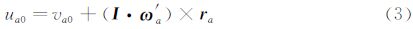
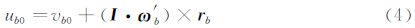
|
| 图 2 碰撞模型示意图 Fig. 2 Diagram of collision model |
碰撞点的法向由薄片间的相对位置决定,碰撞后薄片分 别受到一个沿法向的相等相反的冲量 Im ,作用在2个薄片上的冲量矩分别为

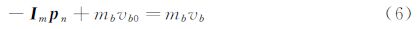
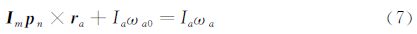
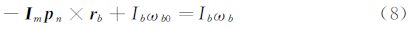

由方程(3)~(9),可得出冲量表达式为:
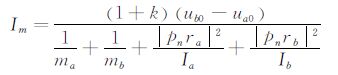
联合以上方程即可得薄片 a、b 碰撞后的速度和角速度。
1.3.3 薄片运动方程 [15]以固定坐标系oxyz为地面坐标系,以薄片质心建立Cξηζ为薄片的弹体坐标系,ψ、θ、φ为物体相对弹体平动坐标系的欧拉角,则根据刚体运动方程可列出薄片质心运动方程,用矩阵形式表述为:
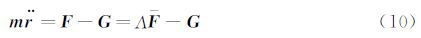


式(10)中,
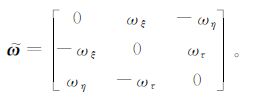
式(12)中
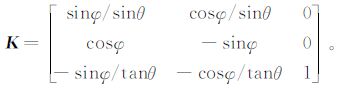
联合方程(10)~(12)可知,如果已知薄片初速度、及所受空气动力即可确定薄片的运动轨迹。
1.3.4 流固耦合方法及碰撞加入方法采用弱耦合的方法分别独立求解流体方程和运动方程,通过流固边界交互数据。在一个计算步长内首先求解流体方程。流体控制方程把计算出来的气动力传递给固体运动方程,固体运动方程根据气动力把计算出来的固体边界位置和速度传递给流体控制方程和网格控制程序,网格控制程序控制固体边界的移动、转动并对畸变率大的网格进行重构等等。碰撞检测程序在网格控制程序之后运行。碰撞检测程序经过预判定后,若无法确定是否发生碰撞启动精确判定程序。精确判定程序调用薄片边界所有网格点位置变量,求解两薄片间的最小间距,若最小间距小于警戒距离,则启动碰撞模型,得出新的薄片运动参数并返回给流体方程与固体运动方程。否则,进行下一步计算。
2 数值计算与结果分析 2.1 计算模型与网格在高速动态下的薄片分离过程中非定常作用明显,薄片间的扰流复杂,气动力作用明显,碰撞频繁,与低速静态抛撒分离过程差异很大。
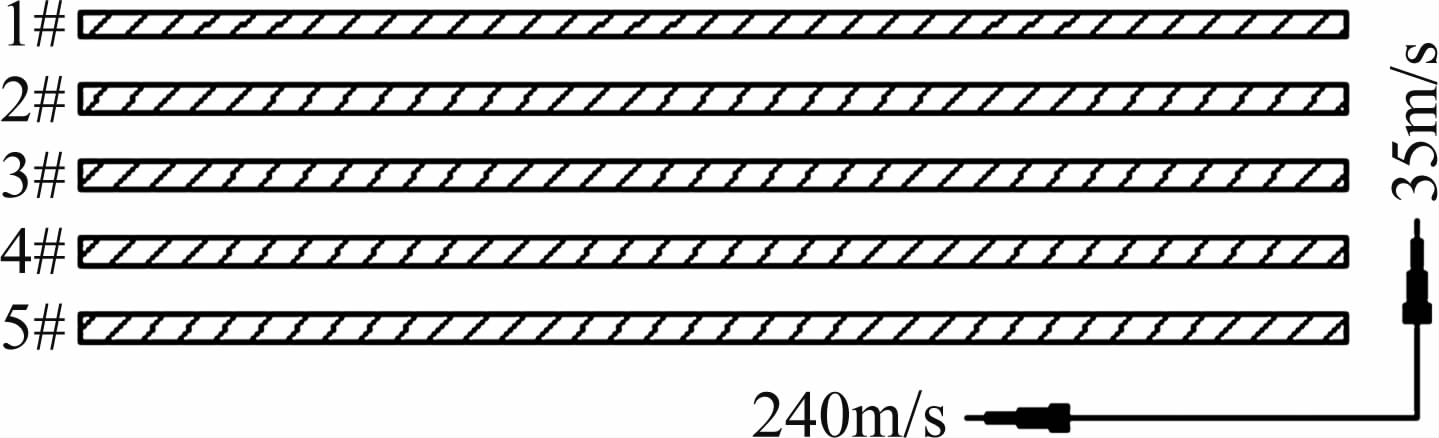
数值模拟的薄片模型取直径 d =50 mm,质量为1 g的均质薄片,与抛撒试验模型一致,厚度为1 mm。薄片间距为2 mm。如图 3所示,5片薄片在发射筒 中以35 m/s速度射出,受到飞机牵连速度为240 m/s,根据相对 速度原理,在流场仿真计算中给定流场速度 x 方向为-240 m/s,y 方向为-35 m/s,薄片集束自下而上分别编号为1#~5#。初始计算网格如图 4(a)所示,薄片间间隔采用加密处理,其最小尺寸为1/200d,其他部分网格用比例函数放大,为保证网格质量,放大系数不宜超过1.2。
|
| 图 3 薄片抛撒模型示意图 Fig. 3 Diagram of computational models |

|
| 图 4 五片分离过程 xy 截面网格重构变化图 Fig. 4 Gird of five plate reconstruction |
多薄片的分离流场仿真是包含多个运动边界的双向流固耦合问题,而且这种运动边界是厚径比很小的薄片状物体,在高速流场中加速快,速度高,对网格划分和网格重构要求较高,必须以较小的时间步长来进行仿真。兼顾工作站计算能力和流场计算的准确性,通过对小数量的薄片分离流场进行仿真,来对薄片的分离过程进行仿真研究。
图 4为五薄片分离过程 xy 截面的网格重构变化图。薄片附近网格采用函数加密处理,网格重构均匀,计算模型初始网格为200万,能很好地反映出流场的变化。随着动边界的移动和转动,边界层网格经过弹簧近似与重构,网格数量会逐渐增加,在2 ms后达到800万。更新后的网格能够满足流场计算条件,所获得的流场计算结果收敛程度较好。
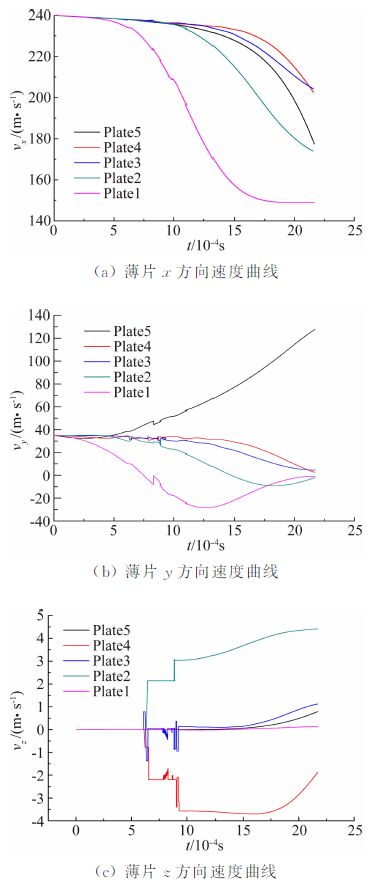
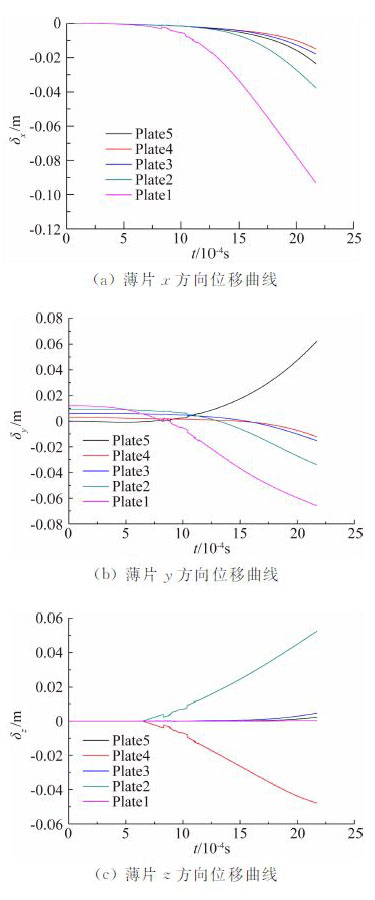
图 5为五个薄片分离过程各时刻流场流线与压力云图,反映了多薄片在分离过程中位置变化和姿态。结合图 6薄片的速度变化曲线与图 7薄片运动的位移时间曲线可以看出,在 xy 方向上薄片多体的干扰明显,脱离主体后减速过程迅速,其加速度大小和薄片自身所处位置和姿态关系最为密切。不受主体段遮挡气流的脱离薄片,最大加速度可达100 000 g以上。头部薄片在气动力的作用下从集束上方脱离,其余薄片从集束尾部脱离。从尾部分离的薄片分离次序规律,其位移变化趋势相似,通过统计分析得出相邻薄片间分离时间间隔约为0.6 ms。在 z 轴方向上薄片的运动受碰撞作用的影响,速度改变量较大,但在集束薄片初始分离阶段其位移与速度变化相对较小,所以在初始分离阶段以 xy 方向的分离为主。

|
| 图 5 五片多体分离过程 xy 截面压力云图 Fig. 5 Pressure cloud imagery of five plate multibodies separation course cross the xy section |
|
| 图 6 薄片运动速度时间图 Fig. 6Speed of plates change with time |
|
| 图 7 薄片运动位移时间图 Fig. 7 Displacement of plates change with time |
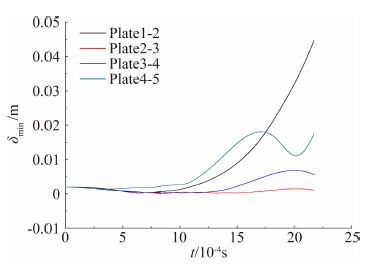
图 8为相邻薄片最小间距时间。碰撞接触虽然在分离初期1 ms内频繁发生,结合图 6薄片运动速度曲线可以看出,碰撞产生的速度阶跃在 x、y 运动方向并不明显,并没有大幅度改变整体运动趋势,在薄片 z 运动方向上速度阶跃较大,但是相对于 x、y 方向上的运动,其速度低、位移小,不足以改变其运动趋势。所以碰撞并不是分离的主要原因,碰撞并没有改变薄片分离的次序,但是碰撞产生的角速度与速度变化导致薄片间的差异性运动加快了薄片的分离过程。薄片多体间干扰明显,脱离主体后减速过程迅速。尾部薄片分离次序规律基本遵循依次逐片分离的次序。
|
| 图 8 相邻薄片最小间距时间图 Fig. 8 Minimum distance between adjacent plate change with time |
通过建立ALE有限体积法描述下的三维可压缩方程,耦合刚体运动方程,并加入碰撞判定与碰撞响应模型,数值模拟了高速下集束薄片的三维非定常初始分离过程。通过仿真分析得出以下结论:
(1) 把碰撞问题加入到了流固耦合计算中,通过仿真模拟了高速下薄片群自干扰弹发射筒弹射后的三维非定常初始分离过程,该仿真模型可用于包含多个运动边界的流固耦合与碰撞问题的流场问题求解。
(2) 分析了薄片高速下多体分离中流场变化与薄片姿态的运动及薄片间的最小间距变化,薄片集束分离初期碰撞频繁,扰乱了薄片的一致性运动,加速薄片分离过程,但是薄片的分离次序主要受薄片间的多体干扰影响。
(3) 特征段多薄片分离次序基本稳定,在空间上薄片集束头部先脱离,尾部遵循依次脱落的分离过程,并通过统计分析得出了时间上的分离时序规律,可为薄片云团的仿真提供理论基础。在下一步的工作中我们将根据仿真得出的薄片分离规律来对薄片云团的散布分离过程做进一步的仿真。
| [1] | Gan Y L, Jiang C, Liu Y J, et al. Development of foreign airborne IR decoytechnology[J]. ElectroOptic Technology Application, 2013, 28(6): 1317. (in Chinese)淦元柳, 蒋冲, 刘玉杰, 等. 国外机载红外诱饵技术的发展[J]. 光电技术应用, 2013, 28(6): 1317. |
| [2] | Fu X H, Fan Q L. Research on modeling and simulation of special material decoy[J]. ElectroOptic Technology Application, 2013, 28(6): 81. (in Chinese)付晓红, 樊秋林. 面源红外诱饵的建模与仿真研究[J]. 光电技术应用, 2013, 28(6): 81. |
| [3] | Zhao F Y, Lu S, Jiang C, Research on the modeling method of surfacetype infrared decoy[J], ElectroOptic Technology Application, 2012, 27(2): 66. (in Chinese)赵非玉, 卢山, 蒋冲. 面源红外诱饵仿真建模方法研究[J]. 光电技术用, 2012, 27(2): 66. |
| [4] | Chen N G. Moving characters simulation of foils cloud used in opticsElectronic countermeasure[J]. Aerospace Electronic Warfare, 2008, 24(5): 20. (in Chinese)陈乃光. 光电干扰箔片云团运动规律的仿真研究[J]. 航天电子对抗, 2008, 24(5): 20. |
| [5] | Wang F J. The analysis of computational fluid dynamics[M]. Beijing: Tsinghua University Press, 2011. (in Chinese)王福军. 计算流体动力学分析[M]. 北京: 清华大学出版社, 2011. |
| [6] | Huang B, Wang H, Tao R Y. Numerical study of multiplatesseparating flow and characteristics[J]. Acta Aerodynamica Sinica, 2013, 31(2): 213218. (in Chinese)黄蓓, 王浩, 陶如意. 薄片分离过程流场特性的数值仿真研究[J]. 空气动力学学报, 2013, 31(2): 213-218. |
| [7] | Zhu B, Zhu X P, Zhou Z, et al. Simulation of unsteady multibody flowfield involving relative movement based on unstructured mesh[J]. Acta Aerodynamica Sinica, 2013, 31(2): 181185. (in Chinese)朱冰, 祝小平, 周洲, 等. 基于非结构动网格的多体分离数值仿真研究[J]. 空气动力学学报, 2013, 31(2): 181-185. |
| [8] | Duan X P, Chang X H, Zhang W P. A CFD and 6DOF coupled solver for multiple moving object problems based on dynamic hybrid gird[J]. Acta Aerodynamica Sinica, 2011, 29(4): 447452. (in Chinese) |
| [9] | Batina J T. Implicit fluxsplit Euler schemes for unsteady aerodynamic analysis involvingun structured dynamic meshes[R]. NASA TM102732, 1990. |
| [10] | Guo Z. Numerical method with multibody forunsteady flows with moving boundaries[D]. National University of Defense Technology, 2002. (in Chinese)郭正. 包含运动边界的多体非定常流场数值模拟方法研究[D]. 国防科技大学, 2002. |
| [11] | Zhang Y D, Ji C Q. Numerical methods with dynamic structured meshes forunsteady flows with moving boundaries[J]. Chinese Jouranal of Computational Physics, 2006, 23(2): 165170. (in Chinese) |
| [12] | Banerjee A K, Dickens J M. Dynamics of an arbitrary flexible body in large rotation and translation[J]. Journal of Guidance, Control and Dynamics, 1990, 13(2): 221227. |
| [13] | Huang B, Wang H, Wang S, et al. Flow field characteristics of multiplates interference in descent[J]. Journal of Ballistics, 2012, 24(1): 4146. (in Chinese)黄蓓, 王浩, 王帅, 等. 薄片状体沉降过程中的多体干扰流场特性[J]. 弹道学报, 2012, 24(1): 4146. |
| [14] | Lin J Z. Multiphase fluid dynamics of extraordinary particle[M]. Beijing: Science Press, 2008. (in Chinese)林建忠. 超常颗粒多相流体动力学[M]. 北京: 科学出版社, 2008. |
| [15] | Pu F. Exterior ballistics[M]. National Defense Industry Press, 1980. (in Chinese)浦发. 外弹道学[M]. 国防工业出版社, 1980. |


