2. 中国空气动力研究与发展中心高速空气动力研究所, 四川绵阳 622762;
3. 中国航空工业集团公司第一飞机设计研究院, 陕西西安 710089
2. High Speed Aerodynamic Institute of China Aerodynamics Research and Development Center, Mianyang 622762, China;
3. The First Aircraft Institute, Aviation Industry Corporation of China, Xi'an 710089, China
0引言
飞机表面的流动包括层流和湍流两种状态,在相同雷诺数条件下,层流摩擦阻力远远低于湍流摩擦阻力。对现代大型民机,约50%的阻力来自于空气与飞机表面的摩擦阻力,采用层流机翼设计和层流短舱设计可以降低摩擦阻力30%左右。目前面向民机设计的层流技术主要有自然层流(Natural Laminar Flow,NLF)、层流控制(Laminar Flow Control,LFC)和混合层流控制(Hybird Laminar Flow Control,HLFC)技术,其中自然层流技术主要通过机翼翼型的专门设计(如设计有利压力梯度,抑制流向T-S波增长,推迟流动转捩等)以产生大范围层流区。美国NACA早在20世纪30年代就开展了自然层流翼型的研究,但由于当时飞机的制造工艺原因,风洞试验已证实的层流翼型的特点在飞行试验中并没有得到实现。从20世纪70年代开始,各航空强国都投入大量精力开展层流技术及飞行试验研究,取得了一系列成果[1, 2, 3, 4, 5, 6, 7, 8, 9, 10],有效地促进了亚、跨声速自然层流机翼设计技术与应用研究。在2009年召开的国际航空运输协会会议上,提出了航空业2020年减排目标,对新一代民用飞机的气动减阻技术研制提出了较高要求,自然层流设计技术再次受到各国关注,如欧盟开展了TELFONA计划 (Testing for Laminar Flow on New Aircraft)和 NACRE计划(New Aircraft Concept Research)和美国NASA开展了ERA项目(Environmentally Responsible Aviation)研究 [11]等。
基于CFD(Computational Fluid Dynamics)的数值优化是自然层流机翼设计较为有效的方法,它集成了数值模拟、优化算法和参数化建模方法等内容。在优化算法方面,基于梯度的寻优算法、进化类算法和响应面方法是在工程优化研究领域内较为常用的方法。由于飞行器优化设计参数通常较多,对进化类算法(如遗传算法)要求的种群规模较大,而响应面也较难准确构建。基于梯度的优化算法是当前较为有效的方法,如在机翼气动外形优化迭代过程中,正是由这些梯度信息告知下一步寻优方向和步长选择。已有的研究表明,整个优化过程95%以上的时间都耗用在流场求解方面,包括梯度求解时的流场计算,因此流场的计算效率直接决定着整个优化过程的时间消耗,也是优化方法具备工程实用价值的重要考核指标 [12]。波音公司TRANAIR全速势方法在流场求解方面效率较高,被广泛应用于波音系列飞机的优化设计方面 [13]。
本文以TRANAIR软件为优化平台,采用两种参数化建模及动网格方法:非均匀有理B样条(Non-Uniform Rational B-Spline,NURBS)和类函数/型函数变换(Class function/Shape function Transformation,CST)方法,对某自然层流机翼进行了亚声速条件下气动外形优化设计,并对优化效果进行了分析和讨论。
1优化模型对于飞行器气动外形优化设计问题,通常定义目标函数为阻力系数 CD,约束条件为升力系数CL、俯仰力矩系数Cm 和机翼几何约束(厚度、容积等)等分别不小于它们各自初值,同时还要满足自变量设计范围、边界层分离因子和物面变形曲率等其它约束条件的限制。多点优化时,通过不同设计点下的目标函数加权平均构造总的目标函数来实现,并满足不同设计点下的气动、几何约束条件。
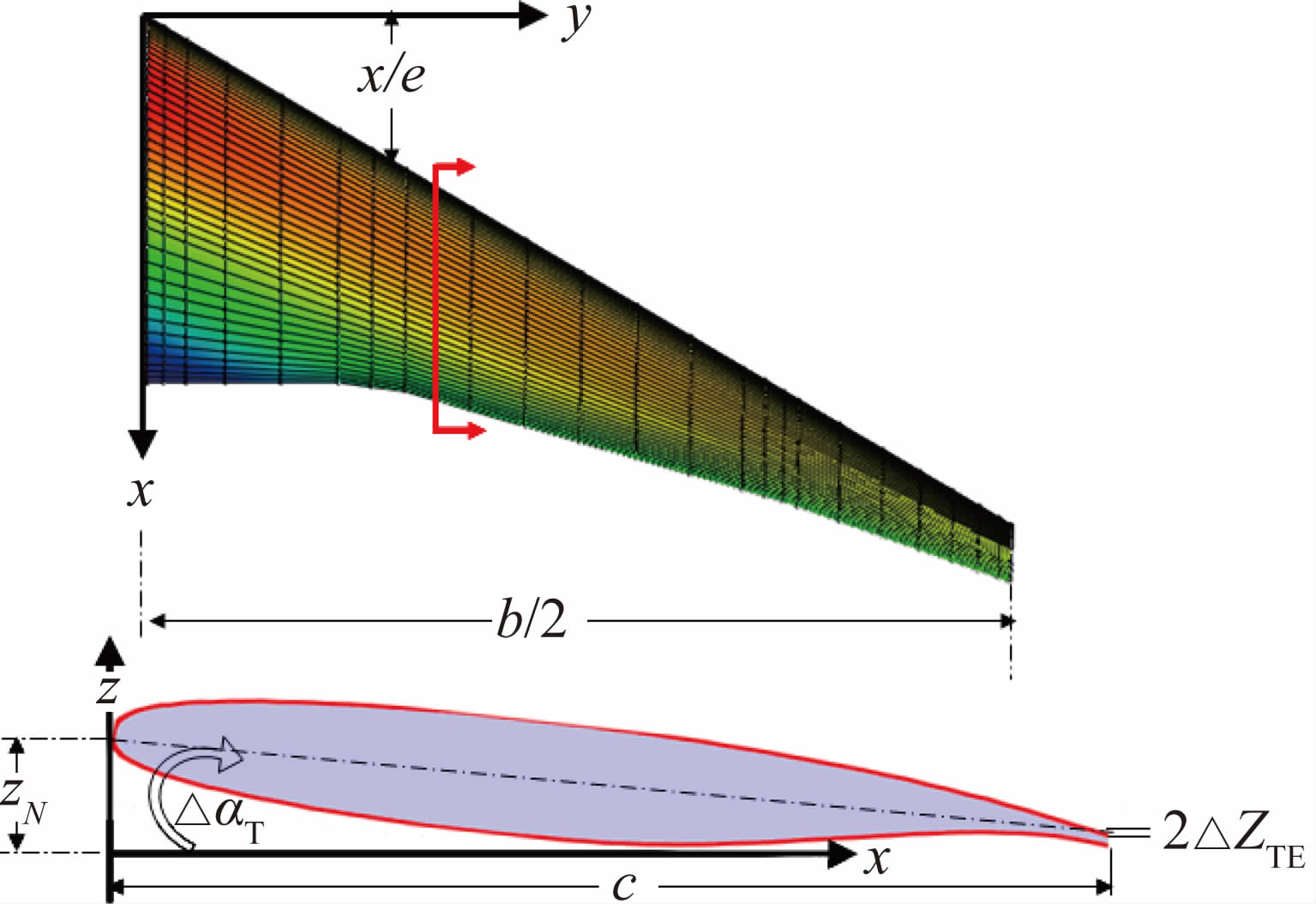
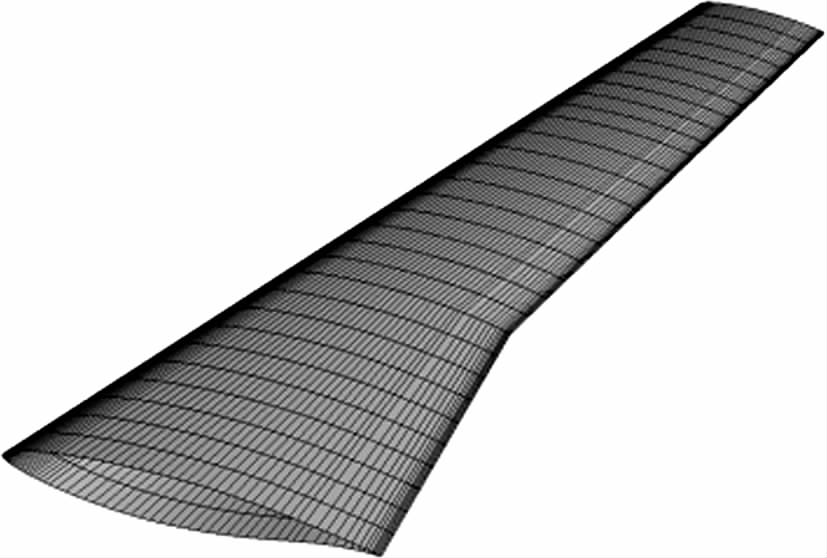
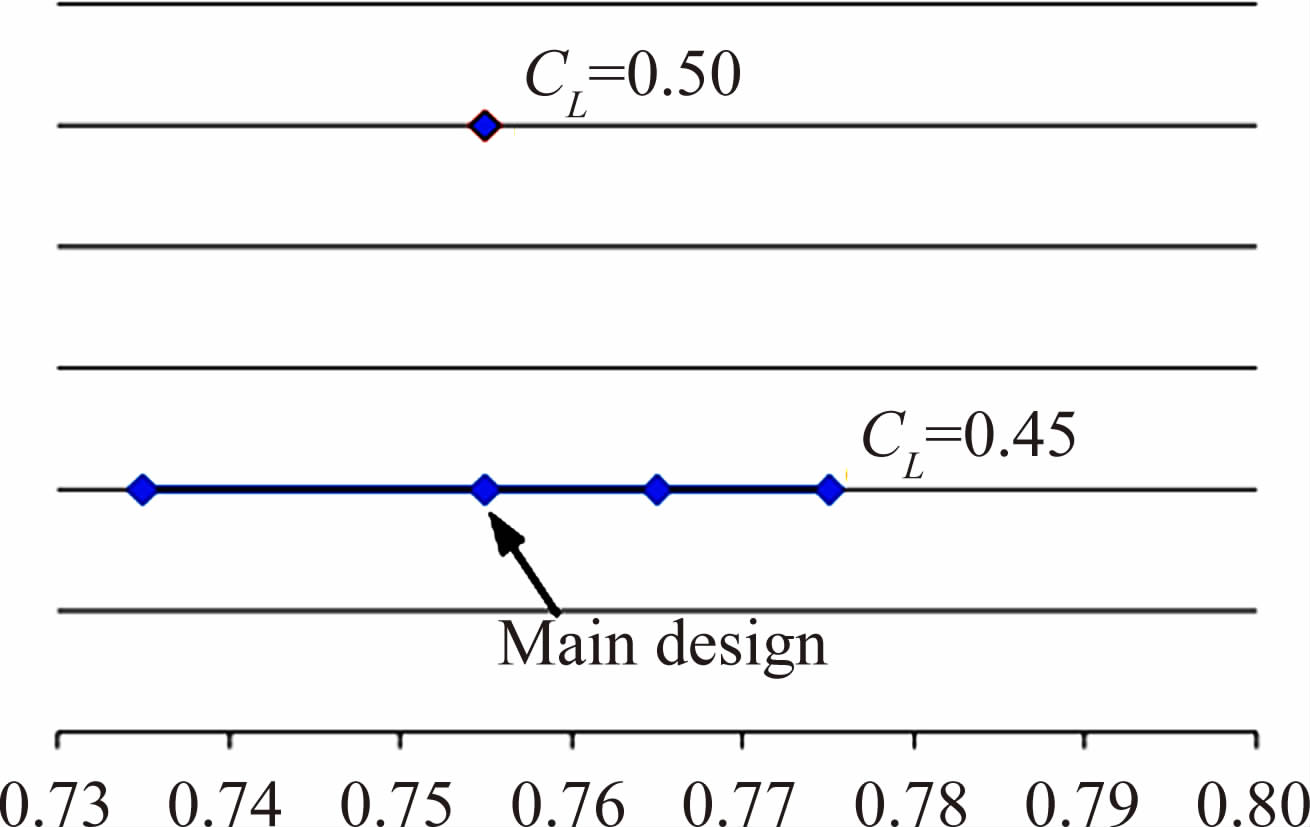
优化算例为某民用通用飞机设计使用的自然层流机翼,其几何外形如图 1所示。机翼参考面积80 m 2,平均气动弦长3.05 m,展弦比10.5,前缘后掠角17.5°,25%弦线后掠角15.6°,后缘内侧后掠角0°,外侧后掠角9.6°,翼根、转折和翼尖处相对厚度分布约13.5%、12%和10%。主设计点为 M=0.755,CL=0.45,Re =18×10 6,多点优化时为五个设计点,其中四个为不同 M数同升力设计点,另外一个为主设计M数时CL =0.50点,如图 2所示。
|
| 图 1 某自然层流机翼 Fig. 1 Natural laminar flow wing |
|
| 图 2 多点优化图示 Fig. 2 Multi-points optimization |
五点优化时,鉴于自然层流机翼的波阻较小,目标函数设置时赋予较小的加权比例,突出总阻力和型阻的比重;约束条件中各设计点下升力和俯仰力矩不得减小,机翼各剖面20%、80%和最大厚度不得减小。其数学模型:
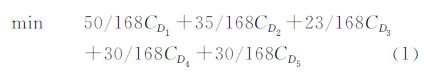

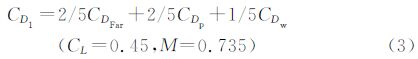
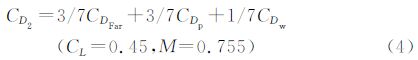
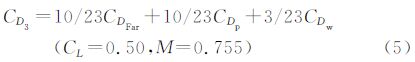
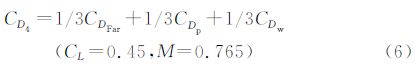
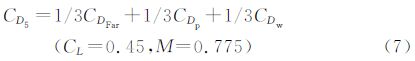
对于一个NURBS曲面,若u方向为p阶,控制点数目为n+1,v方向为q阶,控制点数目为m+1,则:
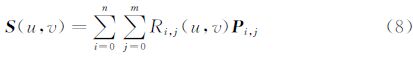
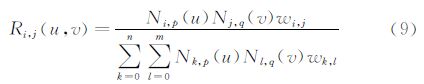
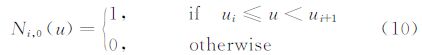
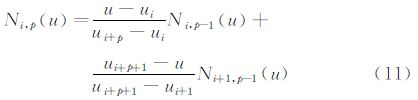
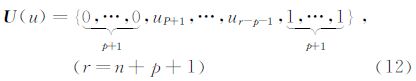
同理可以给出Nj,q(v)和V(v)的表达式。方程式的分段形式,保证了NURBS函数的局域性质,即控制点的变化仅会影响到其附近区域的变化,不会影响到其它区域 [12, 14, 15]。
2.2CST方法在CST方法中,首先将物面的物理坐标用归一化参数表示,然后把参数坐标解析表达成型函数和类函数的乘积,其中类函数用有明确物理意义的典型翼型参数(前缘半径,弯度等)表示,型函数则在类函数的基础上定义特定的几何形体 [16, 17, 18, 19, 20]。其具体表达式为:
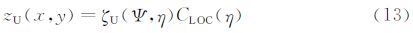
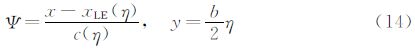
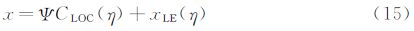
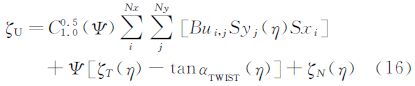
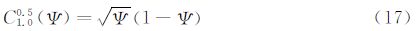
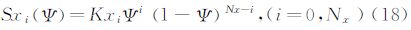
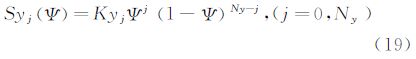
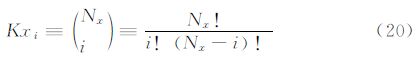
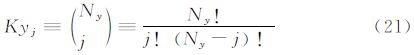
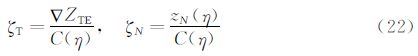
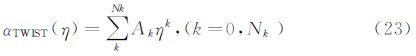
在本文算例中,CST方法使用了四个主控制剖面(翼型),每个翼型上下各使用了9个控制参数,共有72个控制参数实现整个机翼上下翼面的参数化描述。由于NURBS方法更适合空间三维曲面表述,且对于自然层流机翼的精细优化,上翼面的气动外形对阻力影响往往较大,故在NURBS方法中,仅使用30个参数优化上翼面。
2.3优化平台
波音公司TRANAIR软件在工程领域经过大量的测试,具有较好的可信度 [13]。流场求解采用无粘、无旋的全速势方程,层流转捩采用基于线性稳定性理论的 e n 法 [21],并用人工粘性方法进行湍流模拟。优化计算过程中,使用具有自动加密功能的笛卡尔网格,易于物面/空间网格变形及加速流场收敛。
优化算例是在中航工业一飞院曙光服务器上进行,处理器为Dual-Core AMD Opteron(tm) Processor 2220(主频2.80 GHz),内存8G,操作系统为Red Hat Enterprise Linux。TRANAIR软件的核心代码及参数化接口均用计算能力较强的Fortran语言程序开发。由于采用了网格逐渐加密和自适应网格收敛加速技术,虽然两种参数化方法设计变量数目相差一倍,但是时间消耗基本一样。五点优化采用单CPU串行计算,耗时约25~30 h。
3结果分析
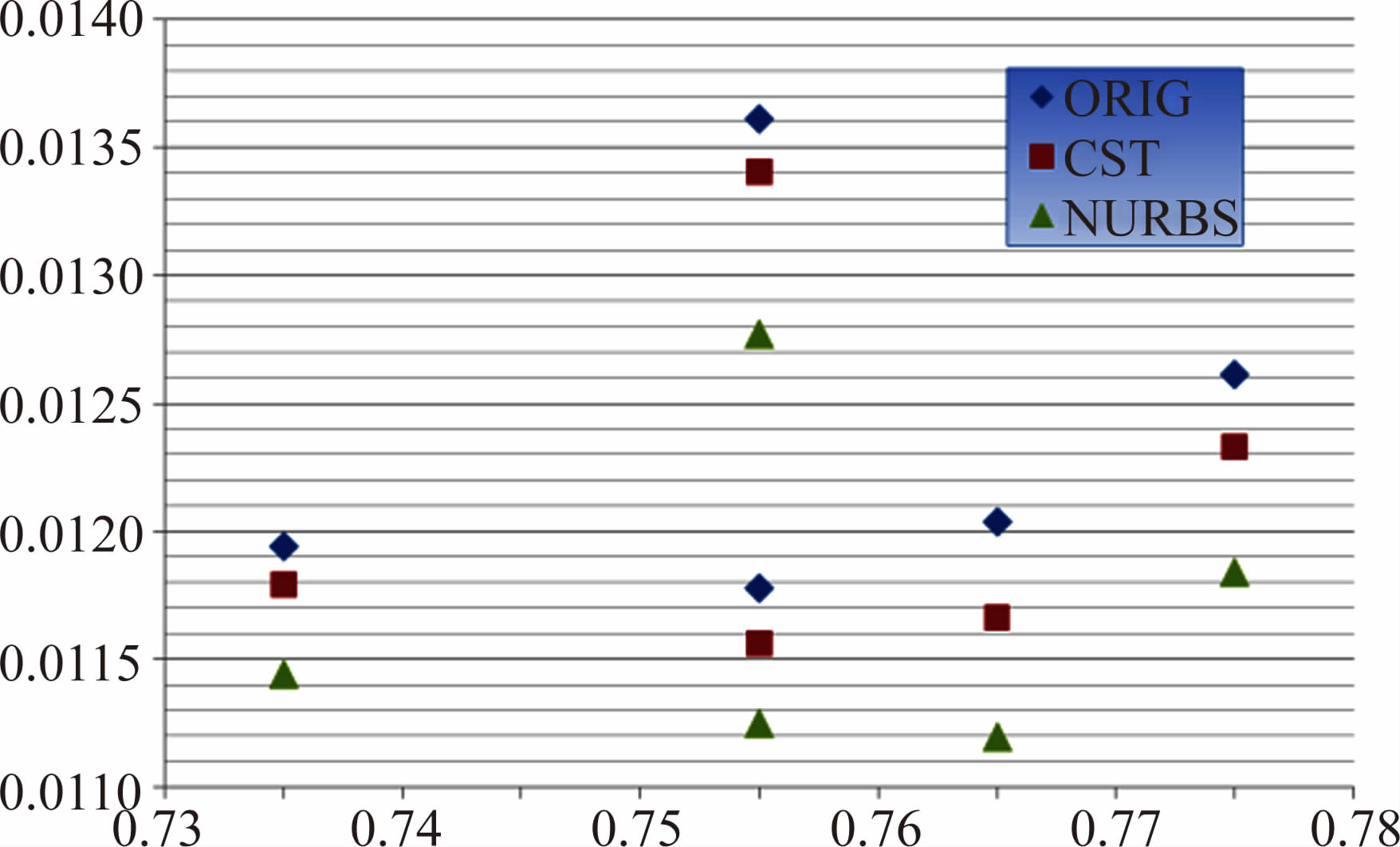
图 4给出了两种参数化方法的优化结果,从中可以看出两种方法优化后阻力都有所减小。主设计点( CL=0.45,M :0.755),CST方法优化后阻力系数减小了0.00022,NURBS方法优化后阻力减小了0.00053,同比分别减小了1.8%和4.5%。并且随着马赫数的增加,优化后阻力减小更加明显,在( CL=0.50,M :0.775)设计点,NURBS方法优化后阻力减小了0.00083之多。单纯从阻力减小量值上看,NURBS方法的优化结果明显优于CST方法。
|
| 图 4 不同参数化方法的优化结果 Fig. 4 Optimization results of different parameterizations |
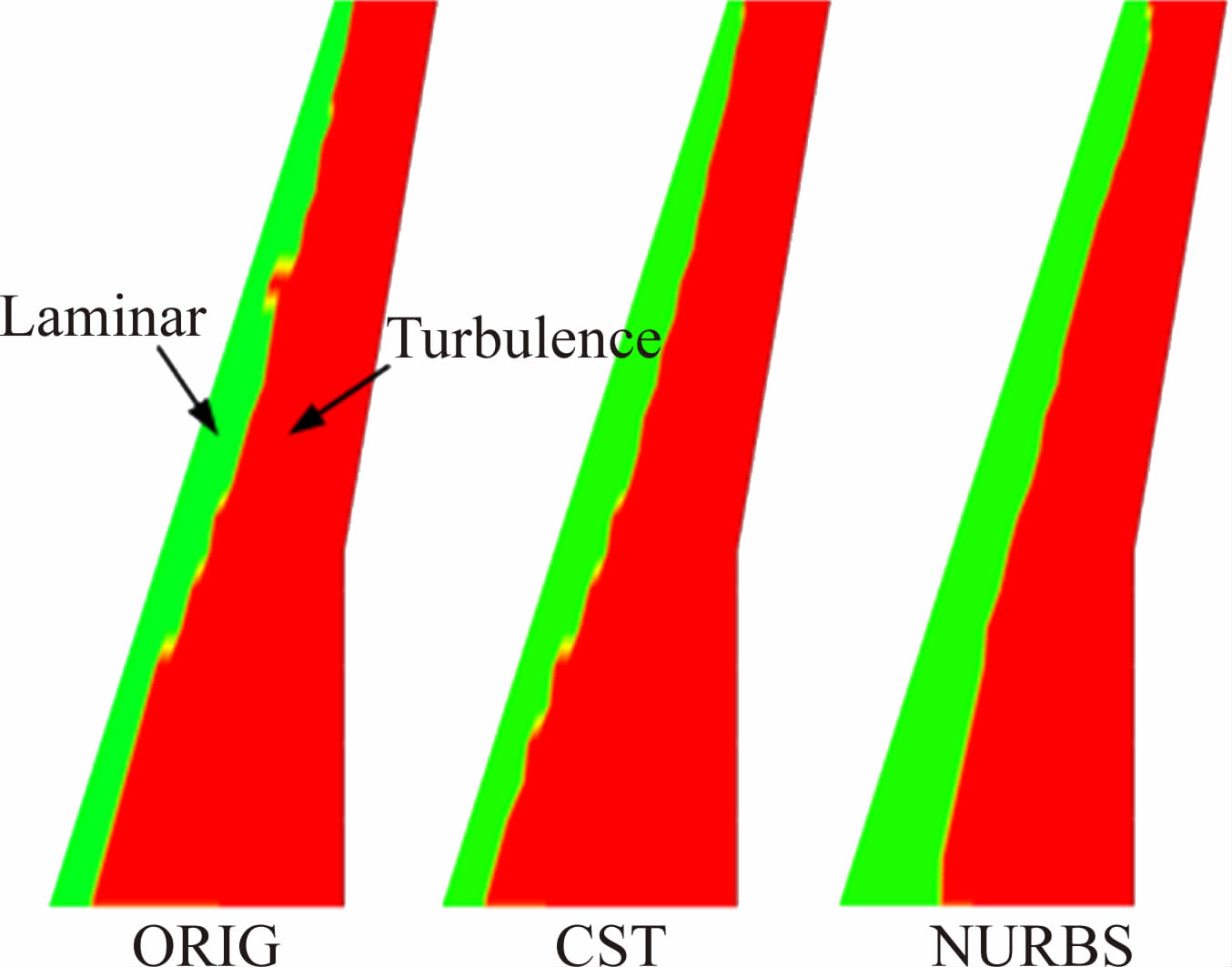
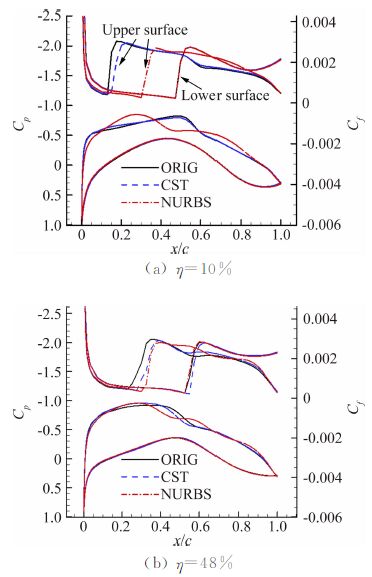
图 5给出了上翼面优化前后转捩位置对比(绿色表示层流区域,红色表示湍流区域)。图 6为优化前后不同展向压力和摩擦阻力对比。从中可以看出,原始的机翼已具备较好的阻力特性,上、下翼面分别有约25%和55%的层流区。在內翼段,优化后转捩位置后移,层流区域变广,图 6(a)10%展长剖面位置对比显示,CST方法优化后转捩位置后移了2.5%当地弦长,NURBS方法优化后则后移达到了18.1%当地弦长;在48%展长剖面位置(图 6(b)),CST方法优化后转捩位置后移了约3.5%当地弦长,NURBS方法优化后则后移了约4.4%当地弦长;在下翼面处,CST方法优化后转捩位置后移了约1.1%,由于NURBS方法并没有优化下翼面,转捩位置几乎不变。
|
| 图 5 优化前后上翼面转捩位置比较 Fig. 5 Laminar flow transition of up wing surface |
|
| 图 6 不同展向压力和摩阻对比 Fig. 6 Pressure and friction coefficient in different spanwise directions |
从10%剖面压力分布上看,翼面上较好的顺压梯度是保证层流区的必要条件。对于上翼面,原始机翼在前缘附近压力减小过快,而后顺压梯度变化较缓,导致转捩过早发生。优化后前缘顺压变化较为平缓,进而延迟了层流转捩,带来较广的层流区域。此外,优化结果显示,上翼面气动外形优化是自然层流机翼精细优化设计的主要方向。
4结论通过对某自然层流机翼气动外形优化设计研究,得出了以下主要结论:
(1) 在本文三维层流机翼优化算例中,与传统基于剖面翼型的参数化方法相比较,面向三维曲面的 NURBS方法的表现出了更好的优化效果,主设计点优化后阻力减小了4.5%。
(2) 机翼翼面上较缓的顺压梯度分布是层流保持的必要条件。
(3) 基于全速势(TRANAIR)的自然层流机翼优化设计方法,多点优化时具有较高的计算效率,工程实用性较强。
| [1] | Arnal D, Archambaud J P. Laminar-turbulent transition control: NLF, LFC, HLFC[R]. RTO-EN-AVT-151, 2008. |
| [2] | Somers D M. Design and experimental results for a natural-laminar-flow airfoil for general aviation applications[R]. NASA TP-1861, 1981. |
| [3] | Holmes B J, Obara C J, Yip L P. Natural laminar flow experiments on modern airplane surface[R]. NASA TP-2256, 1984. |
| [4] | Joslin R D. Overview of laminar control[R]. NASA TP-208705, 1998. |
| [5] | Anderson B T, Meyer R R. Effects of wing sweep on boundary-layer transition for a smooth F-14A wing at Mach number from 0.7000 to 0.825[R]. NASA TM-101712, 1990. |
| [6] | Braslow A L. A history of suction-type laminar flow control with emphasis on flight research[R]//Monographs in Aerospace History, 1999. |
| [7] | Li Q, Duan Z Y, Zhang Y J, et al. Progress in research on natural laminar wing for civil aircraft[J]. Advances in Aeronautical Science and Engineering, 2013, 4(4): 399-406. (in Chinese)李权, 段卓毅, 张彦军, 等. 民用飞机自然层流机翼研究进展[J]. 航空工程进展, 2013, 4(4): 399-406. |
| [8] | Liu P Q, Ma L C, Qu Q L, et al. Numerical investigation of the laminar separation bubble control by blowing/suction on an airfoil at low Re number[J]. Acta Aerodynamica Sinica, 2013, 31(4): 518-524. (in Chinese)刘沛清, 马利川, 屈秋林, 等. 低雷诺数下翼型层流分离泡及吹吸气控制数值研究[J]. 空气动力学学报, 2013, 31(4): 518-524. |
| [9] | Xu P, Jiang C S. Optimization design of UAV laminar aerofoil based on gengtic algorithm[J]. Aero Weaonry, 2009, 1: 7-10. (in Chinese)许平, 姜长生. 基于遗传算法的无人机层流翼型优化设计[J]. 航空兵器, 2009, 1: 7-10. |
| [10] | He J K, Bai J Q, Zhu J. Optimization design of laminar flow airfoil baesd on genetic algorithm and transition model[J]. Aeronautical Computing Technique, 2010, 40(3): 44-47. (in Chinese)何俊奎, 白俊强, 朱军. 基于遗传算法及转捩模型的层流翼型优化设计研究[J]. 航空计算技术, 2010, 40(3): 44-47. |
| [11] | Collier F. NASA’s integrated system research program and environmentally responsible aviation (ERA) project[R]. Eco-aerovision, Uc Davis, 2010. |
| [12] | Ma X Y, Fan Z L, Wu W H, et al. Aerodynamic shape optimization for wing based on NURBS[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(9): 1616-1621. (in Chinese) doi: CNKI: 11-1929/V. 20110419. 1702. 004.马晓永, 范召林, 吴文华, 等. 基于非均匀有理B样条方法的机翼气动外形优化[J]. 航空学报, 2011, 32(9): 1616-1621. |
| [13] | Forrester T J, Edward N T, Yu N J. Thirty years of development and application of CFD at Boeing commercial airplanes, seattle[R]. AIAA 2003-3439, 2003. |
| [14] | Liu R Z, Zhang X D, An B T, et al. Application of non-uniform rational B-spline curve and knot insertion algorithm to turbine blade optimization[J]. Journal of Aerospace Power, 2010, 25(2): 451-458. |
| [15] | Jason E H, David W Z. Integrated geometry parametrization and grid movement using B-spline meshes[R]. AIAA 2008-6079, 2008. |
| [16] | Sripavadkul V, Padulo M. A comparison of airfoil shape parameterization techniques for early design optimization[R]. AIAA 2010-9050, 2010. |
| [17] | Kulfan B M. A universal parametric geometry representation method-CST[R]. AIAA 2007-62, 2007. |
| [18] | Guan X H, Li Z K, Song B F. A study on CST aerodynamic shape parameterization method[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(4): 625-633. (in Chinese)doi: CNKI: 11-1929/V. 20111011. 1411. 005.关晓辉, 李占科, 宋笔锋. CST气动外形参数化方法研究[J]. 航空学报, 2012, 33(4): 625-633. |
| [19] | Zhang L, Chen H Q. Research on genetic algorithm for aerodynamic shape optimization based on CST[J]. Aeronautical Computing Technique, 2011, 41(6): 53-57. (in Chinese)张磊, 陈红全. 基于CST参数化的翼型优化遗传算法研究[J]. 航空计算技术, 2011, 41(6): 53-57. |
| [20] | Kulfan B M. Recent extensions and applications of the “CST” universal parametric geometry representation method[R]. AIAA 2007-7709, 2007. |
| [21] | TRANAIR User′s Manual[M]. The Boeing Company, 2007. |