2. 中国北方发动机研究所, 山西大同 037036
2. China North Engine Research Institute, Datong 037036, China
0 引 言
T型三分支管接头广泛应用于动力工程的管网系统中。与直管、弯管中的流动相比,分支接头处流动呈现较为复杂的流动特性。气流的流动参数如支管与总管流量比以及气体压缩性的不同,会使得管壁附近形成分离区,且不同速度流的湍流混合、冲击挤压等现象不仅形成了使流动的损失增大的局部阻障区,也造成了局部流动压力损失和能量耗散。为了研究流体通过管接头产生的压力损失,国内外学者对分支接头的流动特性[1, 2, 3, 4, 5, 6]、能量转换与损失[7, 8, 9]和流动混合[10, 11, 12, 13, 14]等多方面进行了研究。
试验研究方面,目前应用较广的是ESDU[1, 2]和Miller[3]在早期针对T型和Y型接头测试所获得的定常流数据,但仍不全面,尤其在考虑气体压缩性方面的数据较少;三分支可压缩流方面,较为典型的研究是文献[4, 5]对亚声速空气流经90° T型三分支管接头中的压力损失进行了试验研究,得出压力损失系数不但和支管与公共管之间的流量比有关,还和公共管中的马赫数有关。数值研究方面,文献[6] 采用HFA测试和CFD仿真对T型接头内的冷热两股流体混合现象进行研究,揭示了接头内部轴截面的速度和温度分布,但由于气体流速较低,而忽略了气体压缩性的影响。文献[7, 8, 9]基于对分支接头进行二维流动模型假定,经过公式推导后,得出了压力损失系数理论计算的一般表达式。式子表明,当管接头结构参数一定时,压力损失系数主要和支管与公共管之间的流量比有关。但是在推导过程中,接头中的流体都被假定为不可压缩流体,且当公共管内的马赫数大于0.2时,其压力损失的计算结果和试验结果相差较大。此外,国内研究人员通过数值分析也进行了相关研究[12, 13, 14]。
现有研究主要多集中于不可压缩流、直角T型分支接头流动的研究,对可压缩流、斜T型接头的流动研究较少。另外,对于三分支管接头压力损失的试验研究,国内外多采用冷态试验测量。至于热态试验,对于可压缩流、温度不同的气流汇合也多归结于不同马赫数气流的混合流动,且最终可通过冷态试验中流量比的变化从而来实现等同测量[5]。
针对这种情况,为了分析高马赫数排气通过排气管系三分支管接头时的压力损失情况,本文对两个三分支管接头进行了初步的冷态吹风试验研究,对定结构参数的斜T型三分支管接头在不同流动参数(流量比和马赫数)下,接头处高速气流流动的压力损失进行测试研究。测试结果对于排气管优化设计及管接头一维计算模型建立有着一定的参考意义。
1 试验装置流动试验管路简图如图 1所示。试验的气源由电机驱动的压气机提供。为了防止在试验时压气机发生喘振,压气机后安装一个放气阀。管路中的流量控制阀为闸阀,通过改变阀门的升程来调节不同支路的气流流量。总管段和支管段后分别安装有质量流量传感器,用来测量进入管接头不同支管的气体流量。在三个支管上,分别安装有温度、压力以及压差传感器,用来测量气体温度和压力(各传感器参数见表 1)。

|
| 图 1 分支接头流动试验管路简图 Fig. 1 Schematic diagram of flow test rig |
| 传感器 | 测量范围 | 测量精度 |
| 质量流量传感器 | 0~8000m3/h | ±1% |
| 压力传感器 | 0~300kPa | ±0.5% |
| 温度传感器 | 0~650℃ | ±0.5℃ |
| 压差传感器 | 0~8kPa | ±0.5% |
为了采集接头流动压力损失数据,通过编程,开发数据采集系统。试验时,传感器的输出信号通过MP426高速采集卡同步采集,采样频率为1 kHz。
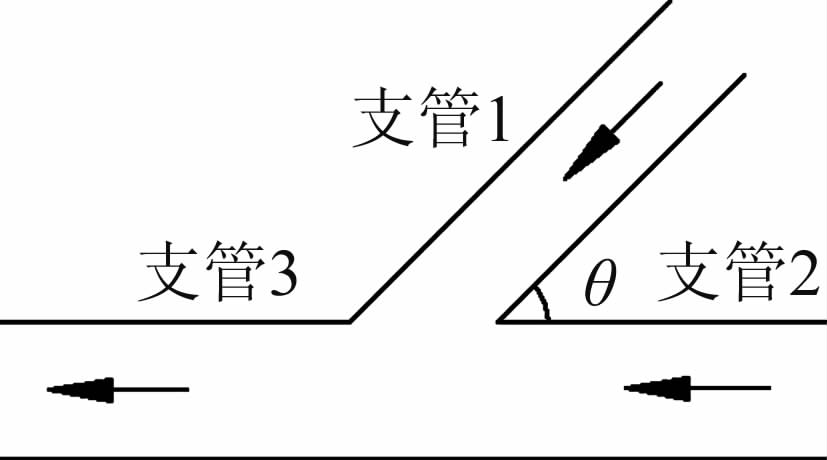
三分支管接头为不锈钢管,如图 2所示,支管1和支管2之间的夹角为45°。分支夹角的交界点处以及支管的转角处都为锐角边缘。试验采用了两套管接头,其支管与主管截面积比φ分别为1和1.56。测试的流型如图 3,两股均匀射流在接头内交汇混合产生复杂的流动特征。理想情况下,压力测量点应尽可能地靠近接头区域。然而,一方面由于临近接头区域,流动变化较为剧烈,同时气流压缩波的交汇与反射比较密集,导致测得的压力数据不稳定;另一方面,由于管内壁摩擦及射流紧缩的作用,测量段过长会导致壅塞作用,从而限制了马赫数的测量范围的扩大。参考其他文献[9],试验中各支管压力及压差传感器测量点的位置均位于距离交汇点3D处(图 2)。测试中,接头的各支管段敷设保温层,以确保接头内的流动尽可能地满足绝热流动条件。

|
| 图 2 三分支管接头示意图 (φ=D1/D3=1) Fig. 2 Schematic diagram of the junction (φ=D1/D3=1) |
试验时,由采集软件监测传感器数据,当管路压力平衡数值稳定后,同步采集各流动参数数据。在不同的总流量工况下,通过调节不同支管管路中的流量控制阀来调节分支接头流动的流量比。支管与总管的流量比控制在0~1之间,间隔0.1。通过调节压气机供气总流量,分支接头流出段马赫数控制在0.1~0.6之间,间隔约0.1。
|
| 图 3 汇合流 Fig. 3 Combining flow in three-pipe junction |
测量数据的处理方法为:首先由各个支管所测得的压力和温度数据计算得出各支管处的气流密度ρ,并结合相应的流量数据计算得出各支管的气流速度u;接着计算各管段的摩擦损失,摩擦系数f利用过渡型圆管的Swamee & Jain 公式[15]计算得出;利用各支管的温度值和气流速度值,计算各支管气流的马赫数,最后利用测量和计算得到的p、m·、T、ρ、u和M等流动参数计算得出各支管总压、流动总压损失和压力损失系数(式(3)和式(4))。
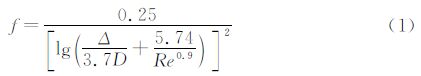
由于分支结构及流动方向的不同,三分支管接头有着不同的流型和压力损失系数。对于试验的测试流型,结果分析中采用的压力损失系数分别为静压损失系数L和总压损失系数K:
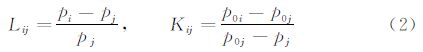
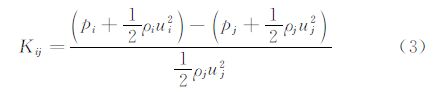
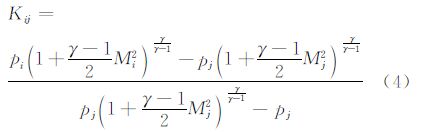
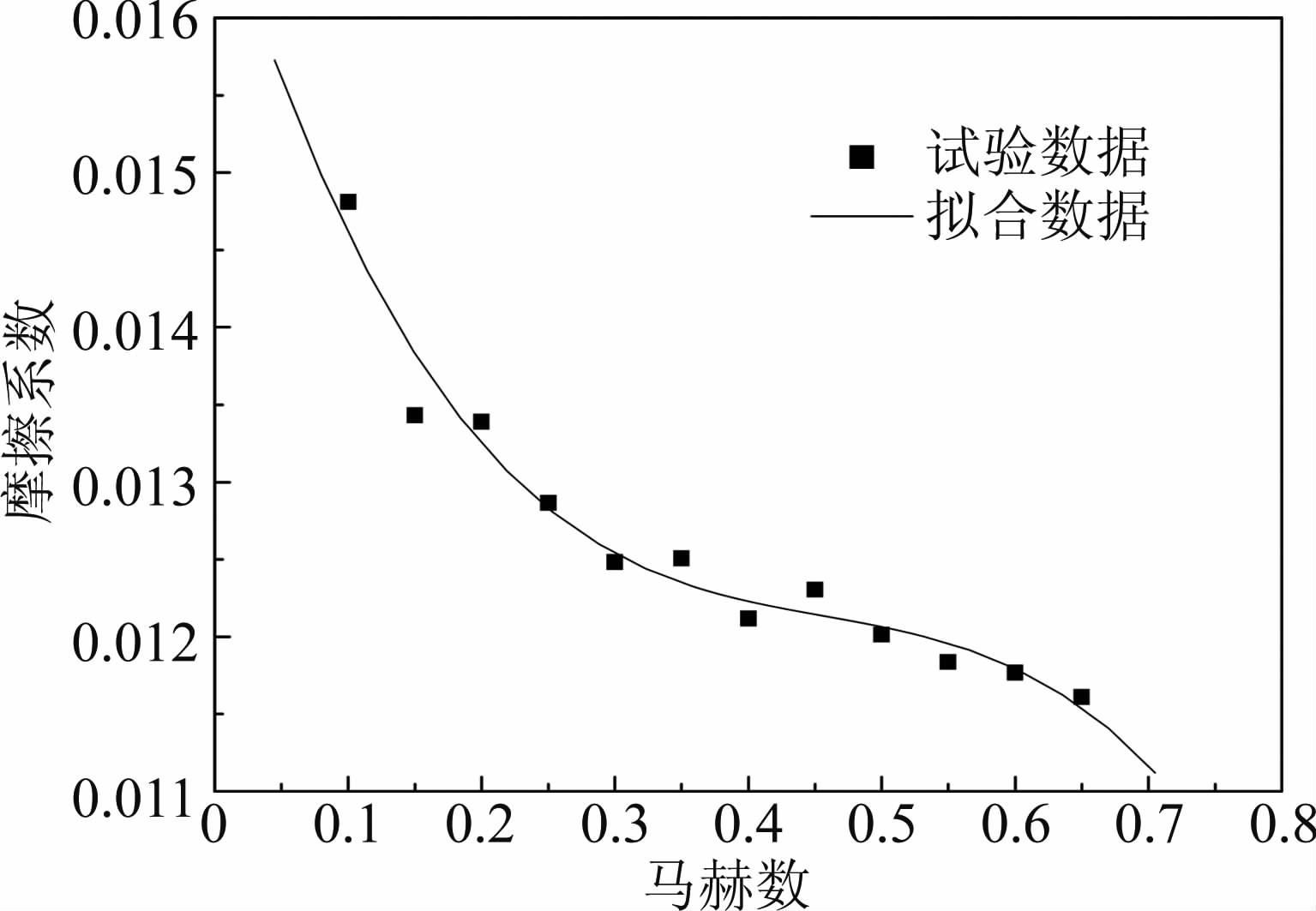
一般情况下,流体流经三分支管接头的压力损失主要由摩擦损失和接头损失组成。在分析流动参数对压力损失的影响前,首先要考虑流动中管道内壁摩擦所带来的影响。为了减少摩擦因素的影响,试验中三通接头采用摩擦较小的不锈钢材料,壁面粗糙高度为5 μm,且设计加工时,分支的交叉点处均抛光打磨光滑。为了获得管接头流动压力损失中摩擦损失值,试验中通过测量支管上不同截面的压力,进而计算得出不同工况下的摩擦系数,如图 4。从图 4中可以看出,对于三通接头中的湍流流动,随着马赫数的增大摩擦系数值逐渐减小,其变化趋势与圆管湍流理论相一致。
另外通过莫迪图中的曲线可以发现,对于光滑管中的湍流流动,当Δ/D为1×10-5到1×10-4,雷诺数为1×105到1×106时,摩擦系数值为0.12到0.195。因此试验中,摩擦因素所带来的压力损失对于三分支总压力损失变化的影响较小,这主要是由于在三分支管接头流动中,造成压力损失主要的影响因素是两股流体射流惯性力之间相互作用,以及考虑压缩性时流体弹性力与惯性力的相互作用,而摩擦力的影响相对较小。这一点与其他公开文献[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17]得出的结论相一致。当然,管内壁面粗糙度和管长等因素影响摩擦损失的大小,而本试验考虑摩擦因素的主要目的是为了减除管接头压力损失中因测量点距接头中心3D距离而造成的摩擦损失那部分数值。
|
| 图 4 马赫数对摩擦系数的影响 Fig. 4 Friction coefficient for different Mach number |
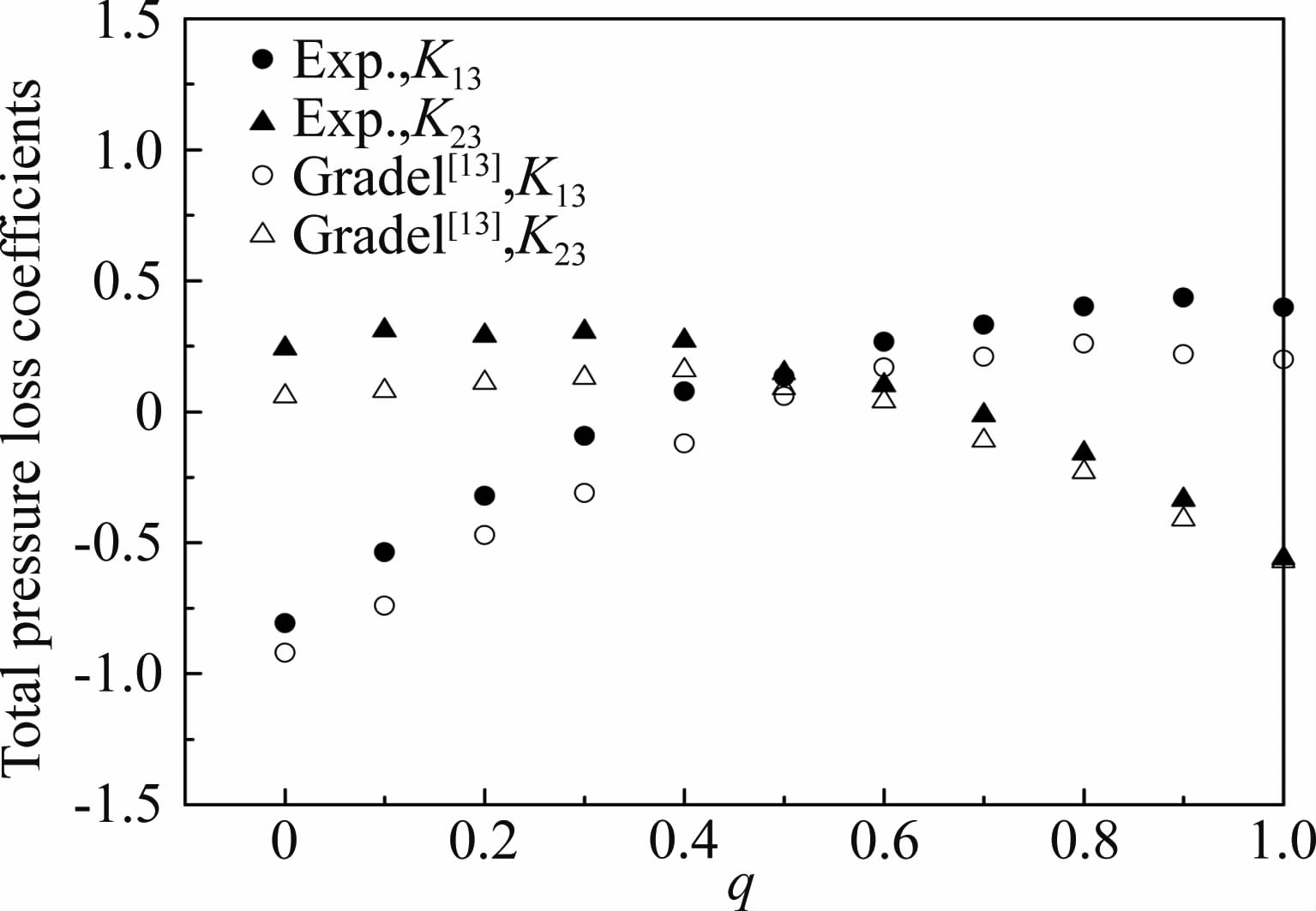
图 5为等面积比接头在出流端气流马赫数M3=0.11时,两流径总压损失系数K13、K23曲线随流量比q的变化曲线图。从图 5中可以看出,在全流量比工况下,试验测量的压力损失曲线与文献[18]中不可压缩流(水流)时的压力损失曲线趋势相同,仅数值上存在较小差异。一个主要的原因是测试接头加工工艺的处理上存在差别,如接头内部的尖锐边缘。尽管在数值上有着一定误差,但两者的吻合度仍足以说明试验台架的可靠性和测试方法的正确性。
|
| 图 5 M3=0.11,φ=1时的总压损失系数 Fig. 5 Pressure loss coefficients for M3=0.11,φ=1 |
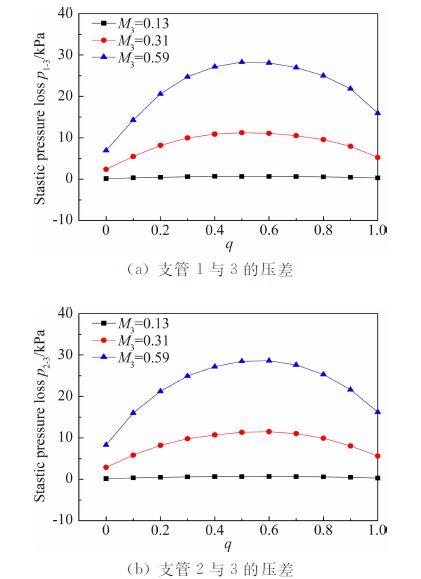
依据入流管端和出流管端的不同,气流通过三分支管接头可分为两个流径。在研究三分支管接头内的气体流动时,也主要是基于对不同流径的压力损失研究。图 6为两流径(1-3,2-3)入流管端与出流管端的压差随流量比变化的曲线图。从图 6中可以看出,在全工况下,三分支入流管端的静压均大于出流管端的静压。这是由于气流的转向、混合和损失等作用使得接头内的流体的动能与压力能存在相互转化。图 6中q为流量比q=$\dot{m}$1$\dot{m}$3,$\dot{m}$1为支管1流量,$\dot{m}$3为支管3流量。
|
| 图 6 入流管端与出流管端的压差 Fig. 6 Pressure difference from branch 1,2 to 3 |
当出流管端气流的马赫数M3=0.13时,支管1与3的压差随流量比的变化较小。而随着马赫数的增加,静压差曲线的抛物线趋势越来越明显,这也说明流量比及马赫数对入流管端与出流管端的压差存在影响。图 6(a)中,当出流管端马赫数一定时,随着流量比的增大,支管1与3的压差先增大后减小。流量比q为0时,压差最小;当q为0.5左右,两管端的压差达到最大值28.3 kPa;q=0时的压差比q=1的压差小,且当流量比一定时,马赫数越大,两管端的压差也就越大。
结合图 6(a)和图 6(b)可以看出,两图的压差曲线近乎相同,因此接头入流端的压力在数值上可认为相等。尽管随着马赫数的增加,支管的流速很高,产生引射效应,两者的压力存在细微差别,但由于在量值上相对较小,仍可认为两者相等。这样在处理可压缩流管接头计算及建立管接头模型时,可使问题得以简化。
尽管从图 6中可以得出压差随流量比及马赫数的变化趋势,但也只能在定性分析上说明流动参数变化对三分支管接头内的流动存在影响。在研究其对流动中压力损失的变化规律时,更多的是要具体分析总压损失系数的变化。
2.3 支管与总管流量比对总压损失的影响在保持三分支结构参数(分支夹角及支管总管面积比)不变的情况下,为了探索支管与总管流量比对接头总压损失的影响,对不同支管与总管流量比时的接头处流动进行了定常试验测试,通过控制流量比来测试分析其对接头处总压损失的影响。
图 7是在不同流量比q时的总压损失系数K13、K23的变化曲线图。由图 7可以看出,总压损失系数K13随着q的增加,先增加后减小,最大值0.52对应的流量比约为0.9,也即是说此时三分支管接头的总压损失达到出流管端动压的一半;而K23先增加后减小,最大值0.37对应的流量比约为0.3。
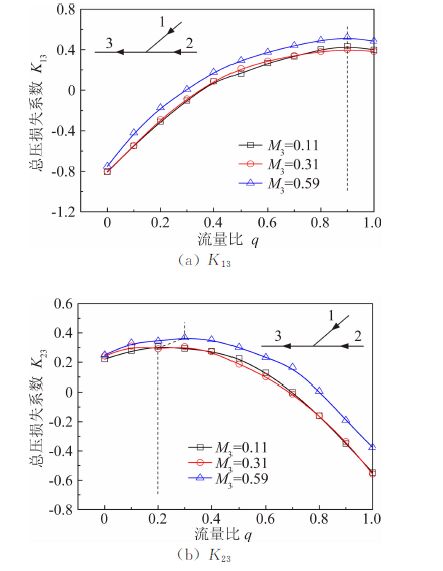
|
| 图 7 流量比对总压损失系数的影响 Fig. 7 Effect of mass flow rate ratio on pressure loss coefficient |
由于支管和总管的流量比将影响在接头内部的流体流向以及两股流体的混合特点,从而影响了局部的速度及压力分布,进而影响了接头处总压损失的变化。对于总压损失系数K13随着流量比q的变化,当q为0时,即支管无气流流入,主管形同直管流动,无气流间的相干作用,此时总压损失最小,且此时由于支管1的总压小于支管3的总压,所以K13为负值;随着q的增大,即支管的流量逐渐增大,气支流对主流的阻滞作用增强,同时两股气流的相干、引射和抽吸作用增强,总压损失也随之增大;当支管流速大于主管时,支管射流穿入主流的深度也随之增加,导致支管射流进入接头处的碰壁损失增大;当q增至0.9时,由两股气流的转向、混合和碰壁等组成的总损失达到峰值;在q等于1时,即气流全部经由支管流入接头,此时流动形同折弯管流动,流动具有很强的湍动性,同时支管气流已经可以撞击管壁,此时碰壁损失最大,但总损失并不是最大,即K13数值上减小。
2.4 出流管端马赫数的影响对于可压缩流动,流体压缩性的影响不可忽略。由于射流紧缩及流动雍塞效应,结合试验条件限制,对几种不同出流端马赫数时的接头处流动进行了定常流试验测试。通过控制进气总流量来调节出流管端马赫数工况,测试分析其对接头处总压损失变化的影响。即M3为0.1~0.6,间隔0.1。图 8为不同出流管端的马赫数对接头的总压损失影响的测试结果。可以看出,出流管端的马赫数对接头的总压损失有着一定的影响。
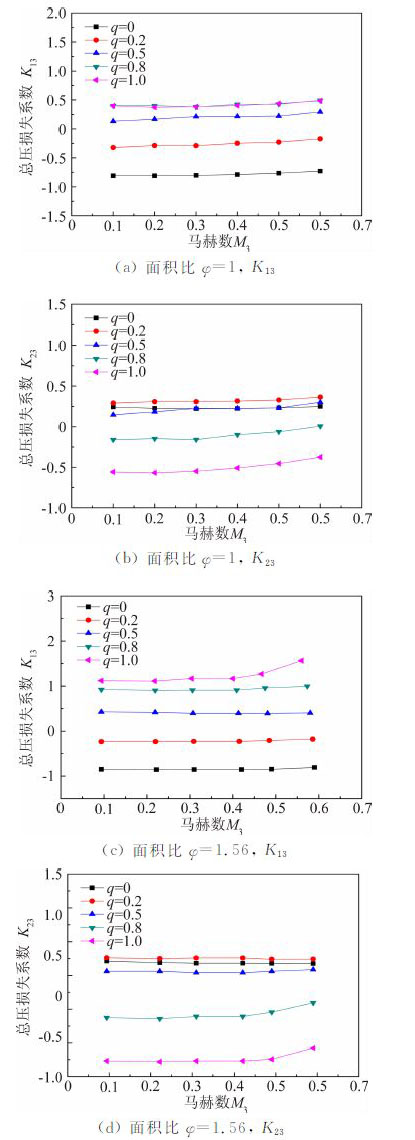
|
| 图 8 马赫数对总压损失系数的影响 Fig. 8 Effect of Mach number on pressure loss coefficient |
在支管与总管流量比一定时,总压损失系数随马赫数的变化有所不同。从图 8中可以看出,其变化趋势主要分为两大区间。当出流管端的马赫数在0.1~0.3之间时,总压损失系数几乎相同,这主要是由于马赫数增加时,总压损失的增幅和出流管端总压与静压差值的增幅相当。随着马赫数的进一步增大,达到0.3以上时,总压损失系数开始增大,这主要是因为当马赫数大于0.3时,气流的压缩性所导致的压力损失开始增加。
表 2给出了q=0.5时,φ=1分支接头两流径的总压损失系数和静压损失系数的测试结果。对于总压损失系数,当马赫数由0.1增加到0.6时,K13由0.153增加到0.294,数值上增加了近一倍,而静压损失系数L13由0.006增加到0.279。表明,随着马赫数的增加,静压损失系数也增加,这是由于流体的压缩性改变了接头内部压力梯度的分布。同时也表明总压损失系数与静压损失系数的变化趋势不同,不能仅以一种参数值的变化来描述接头内部的流动特征。另外,从曲线的疏密程度也可以看出总压损失系数随流量比的变化情况。
| M3 | L13 | K13 | L23 | K23 |
| 0.1 | 0.006 | 0.153 | 0.007 | 0.147 |
| 0.2 | 0.026 | 0.168 | 0.026 | 0.182 |
| 0.3 | 0.061 | 0.197 | 0.062 | 0.226 |
| 0.4 | 0.111 | 0.215 | 0.112 | 0.224 |
| 0.5 | 0.176 | 0.223 | 0.178 | 0.233 |
| 0.6 | 0.279 | 0.294 | 0.281 | 0.302 |
从三分支管接头定常流试验的测试结果可以得出以下结论:
(1) 摩擦对三分支流动总压损失的影响较小,可忽略不计。随着马赫数的增大,即雷诺数的增大,摩擦系数值逐渐减小。当流出端马赫数为0.1~0.6时,对应的摩擦系数值为0.0118~0.0157。
(2) 流径1-3与2-3的压差随着流出端马赫数的增大而增大;随流量比的增大,先增大后减小。且在全工况下,两流径的压差几乎相等,即两流入端的静压几乎相等。
(3) 流动参数影响管接头内部的压力损失。支管和总管流量比将影响接头内部两股气流的汇合流动情况,继而决定了压力损失的变化。总压损失系数K13 、K23随流量比的增大,先增大后减小,但峰值点随工况参数的变化而不同。
(4) 气体的压缩性对三分支管接头的总压损失存在影响。当其他参数一定时,马赫数对总压损失系数存在影响,且当马赫数大于0.3时,总压损失系数逐渐增大。另外,静压损失系数随马赫数的增加幅度比总压损失系数大。
| [1] | EDSU 73022, 73023. Pressure losses in three-leg pipe junctions:dividing flows and combining flows[M]. Engineering Sciences Data Unit. England:London Press, 1973. |
| [2] | Miller D S. Internal flow:a guide to losses in pipe and duct systems[M]. England:Cranfield University Press, 1971. |
| [3] | Abou Haidar N I, Dixon S L. Pressure losses in combining subsonic flows through branched ducts[J]. Journal of Turbomachinery, 1992, 114(1):264-270. |
| [4] | Perez Garcia, Sanmiguel Rojas, Viedma A. New experimental correlations to characterize compressible flow losses at 90-degree T-junctions[J]. Experimental Thermal and Fluid Science, 2009(33):261-266. |
| [5] | Perez Garcia, Sanmiguel Rojas, Viedma A. New coefficient to characterize energy losses in compressible flow at T-junctions[J]. Applied Mathematical Modeling, 2010, 34:4289-4305. |
| [6] | Naik Nimbalkar V S, Patwrdhan A W. Thermal mixing in T-junctions[J]. Chemical Engineering Science, 2010, 65:5901-5911. |
| [7] | Winterbone D E, Peason R J. Theory of engine manifold design-wave action methods for IC engines[M]. London:Professional Engineering Press, 2000. |
| [8] | Bassett M D, Fleming N P, Pearson R J. Calculation of steady flow pressure loss coefficients for pipe junctions[J]. Proceedings of the Institution of Mechanical Engineers, Part C, 2001, 215:861-881. |
| [9] | Bassett M D, Pearson R J, Fleming N P, et al. A multi-pipe junction model for one dimensional gas-dynamic simulations[J]. SAE Paper, 2003-01-0370. |
| [10] | Adeosun J T, Lawal A. Numerical and experimental studies of mixing characteristics in a T-junction micro channel using residence time distribution[J]. Chemical Engineering Science, 2009, 64(10):22-32. |
| [11] | Xin L, Shaoping W. Flow field and pressure loss analysis of junction and its structure optimization of aircraft hydraulic pipe system[J]. Chinese Journal of Aeronautics, 2013, 26(4):1080-1092. |
| [12] | Pu L, Li H X, Wang H J, et al. Numerical simulation of 3D inclined jet to cross flow[J]. Nuclear Power Engineering, 2008, 29:124-128. (in Chinese)卜琳,李会雄,王海军,等.斜向三通管内射流混合特性的三维数值模拟[J].核动力工程, 2008, 29:124-128. |
| [13] | Fang Z Y, Mu H L, Xie M C. Numerical simulation of two dimensional and three dimensional branch junction flow field for compressible flow[J]. Transactions of CSICE, 1996, 14(3):298-301.(in Chinese)方志宇,穆海林,解茂朝.二维三维可压缩流体分支流场的数值模拟[J].内燃机学报, 1996, 14(3):295-301. |
| [14] | Ma X Y, Zhang Z Y, Yang D G. Numerical simulation of arrayed synthetic jets in planar flow field[J]. Acta Aerodynamica Sinica, 2007, 25(4):509-512. (in Chinese)马晓永,张征宇,杨党国.二维合成射流组合效应的数值研究[J].空气动力学学报, 2007, 25(4):509-512. |
| [15] | Swamee P K, Jain A K. Explicit equations for pipe-flow problems[J]. Journal of Hydraulic Engineering ASCE, 1976, 102:657-664. |
| [16] | Costa N P, Maia R, Pinho P T, et al. Edge effect on the flow characteristics in a 90 tee junction[J]. Journal of Fluids Engineering, 2006, 128(6):1204-1217. |
| [17] | Christian A, Selamet A, Miazgowicz K D. Flow losses at circular T-junctions representative of intake plenum and primary runner interface[R]. SAE 2004-01-1414. |
| [18] | Gardel A. Les pertes de charge dans les ecoulements autravers de branchements en te[J]. Bull Tech. Suisse Romande, 1957, 83(9):123-130. |



