2. 海军航空工程学院, 山东烟台 264001
2. Naval Aeronautical and Astronautical University, Yantai 264001, China
0 引 言
20世纪60年代,NASA提出了在飞机头部周线上安装压力传感器阵列,由压力反推大气数据的FADS(Flush Air-Data Sensing,FADS)系统,并取得较好的精度[1]。90年代,Stephen A Whitmore等研究人员在FADS的实时算法[2]、故障检测与管理[3]及系统误差估计[4]等方面的研究取得进展,使FADS技术在多次风洞和飞行验证后趋于成熟[5, 6]。如今FADS系统更是被欧美先进战机广泛使用。近期在无人机X-43A上进行了超声速下算法测试[7],还在Orion返回舱上进行了可行性实验[8],均取得了理想结果,FADS系统运用变得更为广泛。国内对FADS系统的研究相对较晚,且主要集中在FADS系统模型验证[9]、算法的探索改进[10]等方面,尚未达到实用化阶段。但是,FADS系统引气管路的气动模型使传感器的使用范围受海拔高度影响明显,引气管路固有的气动延迟导致传感器采样频率低[11],其理论最优奈奎斯特采样频率仅为12.5 Hz,使得大气参数计算实时性受到影响,尤其飞行器作机动飞行时,攻角、侧滑角的测量精度明显下降。其次FADS系统求解算法也存在发散并导致系统失效的问题[2]。
为了克服传统的FADS系统的缺陷,本文提出了基于气流速度值的嵌入式大气数据测量(Airflow Velocity Based Flush Air-Data Sensing)方法,用可直接测量传感器处气流速度的声矢量传感器替代单纯压力传感器。基于声矢量传感器测得的速度值,建立气流绕钝头体速度场分布模型,确定气流速度、攻角、侧滑角与传感器阵列中各传感器测量速度值的关系,通过策略消元组合求解出攻角、侧滑角。在计算气流速度时,FADS系统是通过复杂迭代运算求解动压、静压,这不仅花费时间而且存在算法发散等问题。本文气流速度的测量上,在得到攻角、侧滑角后可根据模型关系直接求解自由流速度,从而提高了系统的实时性。其中声矢量传感器,是由一个声压传感器、三个两两正交的质点振速传感器组合而成,在空间上同步测量一点处流体声压和三维的质点振速可直接获得传感器处的气流速度信息。荷兰的Micro-Flown公司,已经能提供大小在3 mm、采样频率从0.1 Hz到2 kHz的声矢量传感器[12]。声矢量传感器的较高采样频率为实时求解大气参数提供了保证,即在较高采样频率下,可认为大气参数没有发生突变,利用前一次的计算结果作为后一次计算的输入。目前文献[17]在利用声矢量传感器估计气流速度方面做了理论上的探索,其研究表明:利用声矢量传感器,可直接获取飞行器上传感器处的气流速度。
在可获取传感器的当地气流速度的前提下,建立自由流绕飞行器表面的速度分布模型,并根据该模型推导了攻角、侧滑角和气流速度的表达式,然后利用Fluent仿真数据分析了传感器合理安装位置,依据仿真数据验证了所推导的表达式的有效性。
1 测量原理 1.1 可压缩流的密流模型不可压缩流的势流理论表明,流场的速度满足拉普拉斯方程▽V=0时,可以通过叠加不同的速度势形成新的速度势,即新的流场[18]。其中,任何两条流线不会相交,即可以将流线看成是一个飞行器固体外壁。均匀流场和三维偶极子叠加形成的流场可以得到圆球边界,是绕钝头球体的不可压缩流场。在稳定可压缩流场中,气流满足:


在不可压缩流中,球坐标系下均匀流场与三维偶极子叠加后的速度场可表示为[18]:
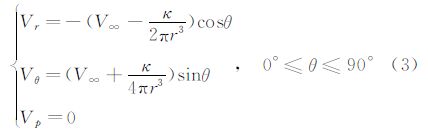
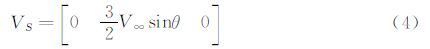
在可压缩流中,将上式中的速度量替换为密流量,有可压缩流场的密流分布:
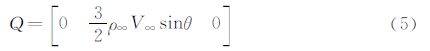

|
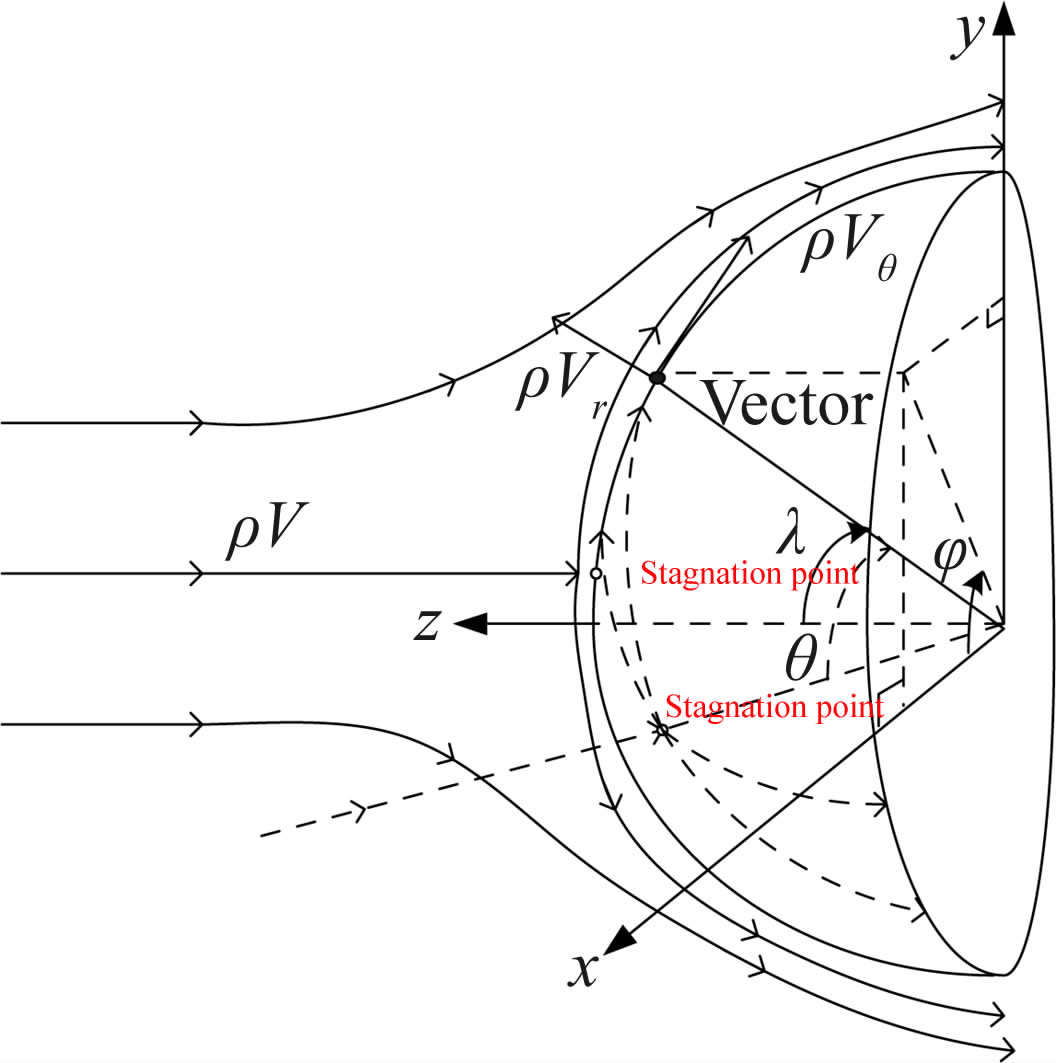
| 图 1 密流绕钝头体分布示意图 Fig. 1 Density flow distribution over blunt head |
考虑到流场的可压缩性,定义压缩性系数Cc=f(Ma)(Ma为马赫数),用Cc代替式(6)的常数项,以校正因马赫数变化给流场压缩性带来的影响,则密流模型为:

由于密度是无法直接测量的,因此在保证密流模型的基础上将其消去。根据热动力学知识,由完全气体状态方程p/ρ=RT,可导出密度和温度的关系$\frac{\rho }{{{\rho }_{\infty }}}$=${{\left( \frac{T}{{{T}_{\infty }}} \right)}^{\frac{1}{r-1}}}$,T∞、T分别为无穷远处来流温度和传感器处温度。在高亚声速条件下(Ma<1),沿流线的流动满足绝热条件的,即使出现激波,在激波前后的流线上任意两点有相等的能量[19],且有能量方程CpT+$\frac{{{V}^{2}}}{2}$=c,Cp为定压比热容,R为气体常数,c表示一常量。在通过任意传感器的一条流线上,选取无穷远处和传感器处的速度与温度值,则该流线能量方程满足:
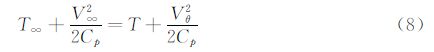
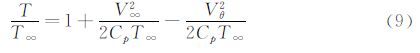
由马赫数定义Ma=$\frac{{{V}_{\infty }}}{a}$,其中声速a与静温间存在a2=γRT∞的关系[19],且有Cp=$\frac{\gamma }{\gamma -1}$R。将马赫数和声速表达式带入到式(9)中,可以得到温度和马赫数关系:
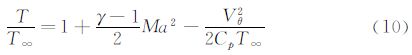
利用密度和温度的关系和式(10),可消去式(7)中的密度项。因此,式(7)变为:
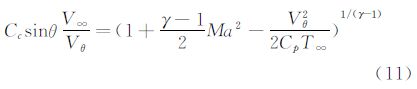
由于方程式(11)是非线性的,一个较好的选择是用消元法化简求解。选取i、j作为下标变量表示第i和j个传感器,因此,传感器处式(11)可写成:
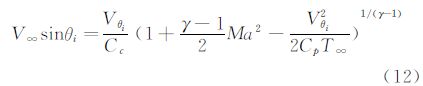
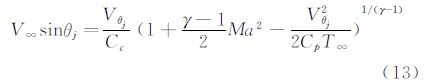
将式(12)和式(13)相除,可以得到:
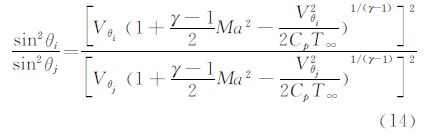
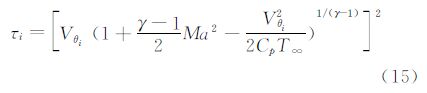

此式为最终的求解模型,它反映了气流入射角与马赫数、传感器处的气流速度以及气流温度的关系。只要知道马赫数、传感器处的气流速度以及气流温度,便可求出气流入射角。又由于气流入射角是关于攻角和侧滑角的函数,因此进一步可求出攻角和侧滑角。
2 攻角、侧滑角和速度的求解 2.1 传感器布局采用声矢量传感器阵列来测量飞行器头部气流参数。阵列位于飞行器的前端,分布情况如图 2所示。再利用锥角、圆周角表示飞行器表面上的传感器在球体模型中的位置。锥角λ是坐标原点和传感器的连线与oz轴正方向的夹角;圆周角φ是xoz平面绕oz轴逆时针转到传感器处的夹角。标号U、D、L、R分别表示上下左右的传感器,其对应的圆周角分别为90°、270°、180°、0°。1、2、3、4标号对应的锥角分别为20°、30°、45°、60°。L=(sinλcosφ,sinλsinφ,cosλ)是传感器在机体坐标中位置矢量。在空气动力学中,待测量的攻角α为翼弦与来流的夹角,此处定义攻角α为来流与xoz平面的夹角。若来流在xoz平面下方,则攻角为正。侧滑角β是来流与yoz平面的夹角,若来流在xoy平面左侧,则侧滑角为正。U=(cosαsinβ,-sinα,cosαcosβ)是自由流(与飞行器的相对速度,也即飞行器的空速)矢量在机体坐标中反方向矢量,它垂直表面向外。气流入射角θ可以用攻角、侧滑角和传感器位置关系满足cosθ=$\frac{LU}{|L||U|}$。因此,θ的余弦可表示为:
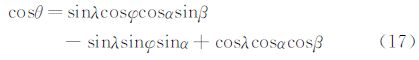
|
| 图 2 声矢量传感器阵列示意图 Fig. 2 Acoustic vector sensors array |
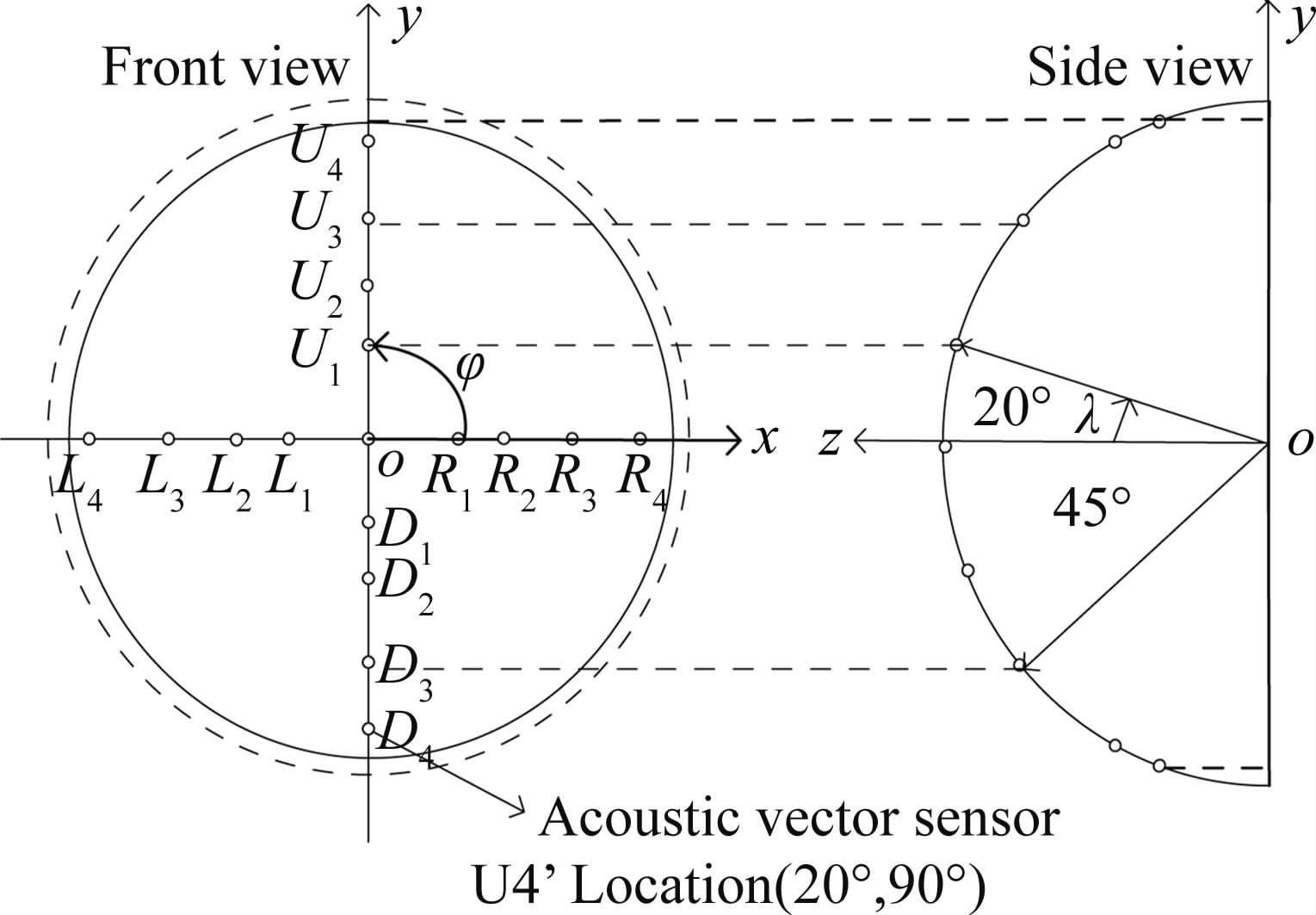
在图 2所示的传感器阵列中,选取φ=0或π的任意三个传感器组成一个侧滑角解算组合。在下面的解算中,采用下标变量i、j、k来分别表示这三个传感器。定义τij=τi-τj,根据式(16),有τij=τicos2θj-τjcos2θi,同理又有关于τjk、τki的表达式。由于τij+τjk+τki=0,故有:
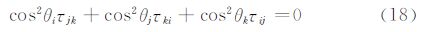
定义符号函数: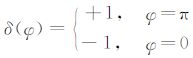 。由于计算中选取了φ=0或π,故式(17)可写为:
。由于计算中选取了φ=0或π,故式(17)可写为:
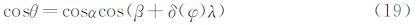
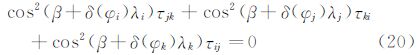
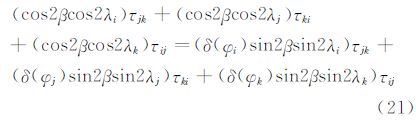


在获取侧滑角β的前提下,可按下述方法求解攻角。设a=sinλcosφsinβ+cosλcosβ,b=-sinλsinφ,则式(17)可简写为:

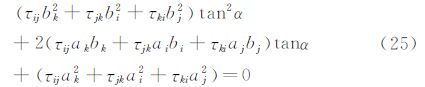
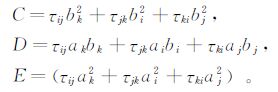
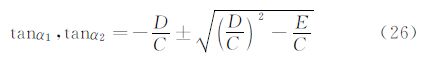
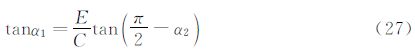
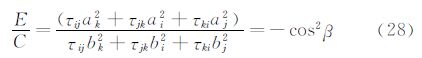
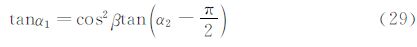
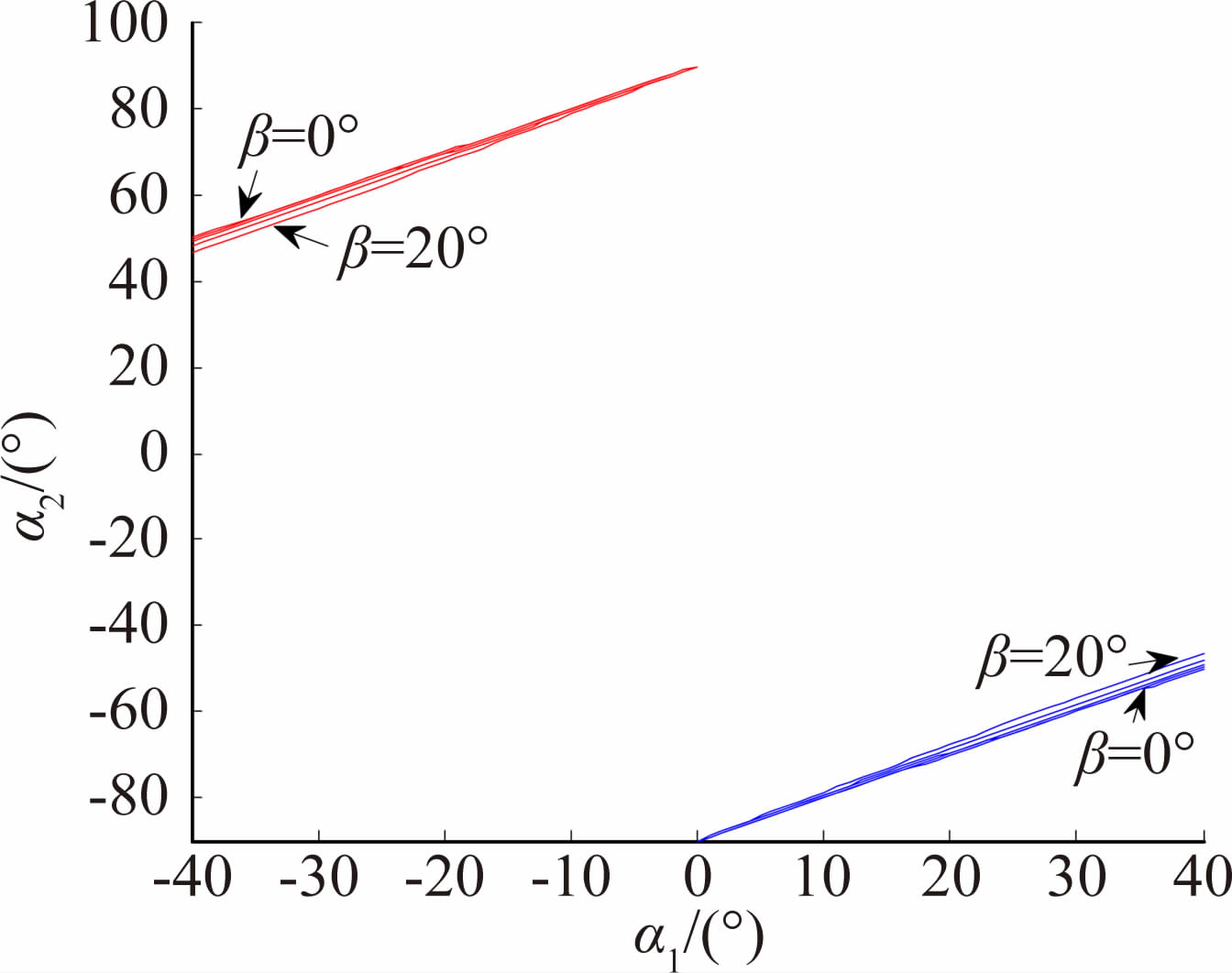
这样得到了两个攻角之间直接关系。在FADS飞行测试中,攻角达到30°以上,侧滑角达到15°以上。图 3给出了式(29)中α1与α2的关系曲线,可以看出,在侧滑角达到20°,α1在0°到40°间变化时,α2始终是密集分布在较大值处。因此在真实飞行条件满足攻角小于40°时,可选取数值较小的攻角计算值为真实解。
|
| 图 3 两攻角关系图 Fig. 3 Relation between two angles of attack |
在侧滑角和攻角解算后,将求解得到的攻角α、侧滑角β带入到式(11)中,可得到空速的表达式:
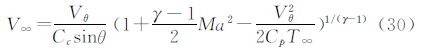
考虑到声矢量传感器具有足够高的采样频率,在采样间隔内飞行器大气参数没有发生突变,即式(30)中马赫数Ma可用前次计算值带入,Cc取值取决于前次的速度值,由此可直接利用式(30)计算出空速值。由于利用式(30)计算空速值不需要迭代运算,实时性将大大提高,并可避免算法发散的问题。
2.4 计算步骤根据上述测量原理,整个算法步骤如下:
设定V∞、T∞、α、β参数的初始值。确定传感器组合,选定一个侧滑角传感器组合,即确定λijk、φijk(λijk表示λi、λj、λj);选定一个攻角传感器组合,即确定λrst,φrst;
第t时刻:
1) 通过声矢量传感器的阵列测量值估计Vθiθjθk,Vθrθsθt;
2) 选定前次V∞、T∞确定Ma、Cc;
3) 根据定义,更新τi、τj、τk,τr、τs、τt;
4) 按式(23)更新β;
5) 按式(26)更新α1、α2并选取数值较小的为α;
6) 带入α、β到式(17)计算θ;
7) 带入Ma、Cc、θijk、θrst到式(30)得V∞ijk,取V∞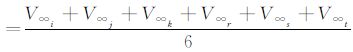 。
。
第t+1时刻,重复上述步骤。
3 计算验证 3.1 Fluent仿真利用矢量传感器阵列测量飞机头部任意位置处的气流速度的方法已经由文献[14, 15, 16, 17]给出,因此本文假定飞机头部传感器处的气流速度可如压力一样直接测量。速度数据的采样,限于实际条件,利用ANSYS14.5下Fluent进行仿真获取。由于传感器安装在机头位置,头部气流不受机身影响,所以只需要了解飞行器头部绕流分布情况。因此,仅用钝头体来模拟飞行器头部的绕流。模型的生成和网格划分使用ANSYS的ICEM CFD前置处理模块来完成,计算及后处理使用Fluent及其完成。
仿真模型:模型及尺寸如图 4所示,以半径为50 mm的半圆为前体,以切线自然过渡总长L为200 mm的旋转体,以25L长度和10L宽度的计算域进行仿真。

|
| 图 4 仿真模型及网格划分 Fig. 4 Simulation model and mesh |
网格划分:由于模型相对规整,因此采用结构网格进行划分[20],结构网格具有生成速度快和质量好的优点,利于获得较好的计算结果。
Fluent模型的选择:在飞行器前缘,其表面有一层非常薄的边界层,边界层在尺度上相对于机身可以忽略。但是在考虑粘性作用时,机体表面设置采样点的取样速度为无滑移的壁面速度,即速度为0,因而无法确定边界层外的绕流速度。在高速飞行状态下,雷诺数较大,惯性力与粘性力相比占主导地位,粘性作用可以忽略,机头附面层非常薄,在导气管路处气流速度可视为不受附面层影响,可以测得无粘场的速度作为传感器处的自由流速度。因此可以在Fluent中用滑移边界对无粘模型进行求解,考虑能量方程,并设置求解器为基于密度的定常模式。
边界条件及计算方法:边界采用压力远场设置马赫数、来流方向、静压等条件[21]。仿真模拟了8 km高度的大气环境,选取介质为理想气体。
3.2 压缩性系数的校正本文测量模型中,压缩性系数Cc需要校正。考虑到模型是具有对称性的钝头球体,因此在不同攻角、侧滑角下,绕流在同一马赫数下具有相同的流场分布,仅相对位置发生了变化,这样就给校正带来了方便。同一马赫数下压缩性系数的校正值,可以作为该马赫数在不同飞行姿态的校正值。在攻角、侧滑角均为0°的情况下,利用传感器处的气流速度可以估计压缩性系数Cc。当α=β=0°,带入到式(17)中,有sinθ=sinλ。根据式(11),有:
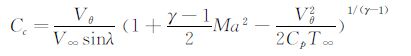
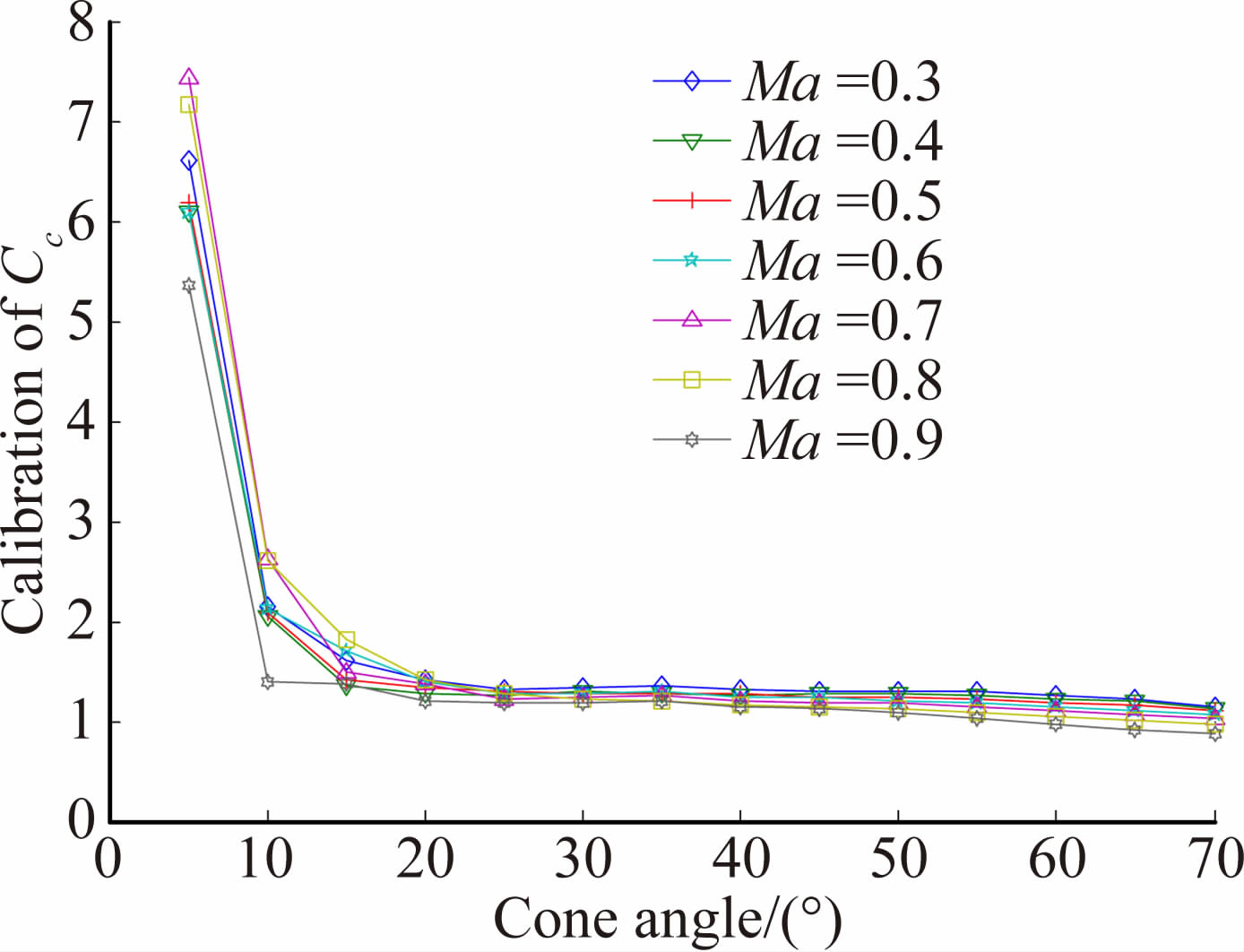
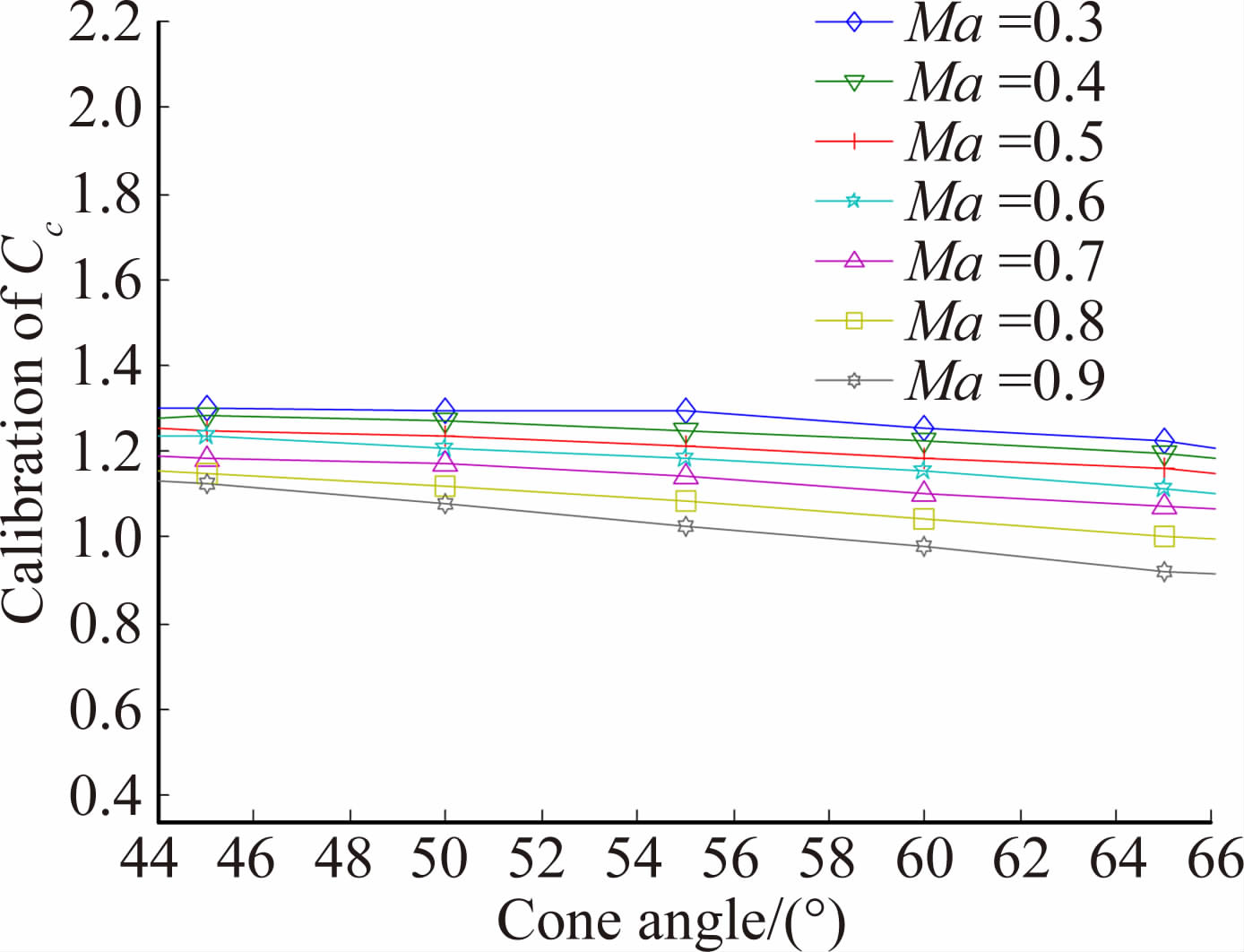
根据图 2所示的传感器阵列测得的传感器处气流速度数据、压缩性系数的估计曲线如图 5所示。从图 5可以看出,对于锥角位于15°范围内的传感器,由其观测值计算所得的压缩性系数较大,而由锥角大于15°的传感器计算所得的压缩性系数较小,且与不可压缩模型的理论值1.5接近。其原因在于:理论上阻滞点的理想速度值应当为0,但经过Fluent仿真采样发现,阻滞点速度值不是0,与理论上的速度值相比,数值偏大,从式(30)可知Cc∝Vθ,导致在阻滞点附近出现了偏大的误差。对图 5进行局部放大后,其结果如图 6所示。可以看出随着马赫数的增加,压缩性系数的估计值逐渐减小。同时,随着锥角的增加,压缩性系数估计值逐渐减小。且随着马赫数的增加,其减少速度略快。这说明此模型在较大入射角处存在一定偏差。
|
| 图 5 α=β=0°压缩性系数Cc Fig. 5 Compressibility coefficients at α=β=0° |
|
| 图 6 α=β=0°压缩性系数Cc局部放大图 Fig. 6 Partially enlarged view of compressibility coefficient at α=β=0° |
因而在选取传感器组合时,应选取气流入射角大于15°的传感器较为有利,实际计算中可以舍弃全体采样速度值较小的传感器测量值,保留其余值作为有效的计算值。
3.3 攻角、侧滑角验证为验证文中提出的攻角、侧滑角表达式的有效性,设置攻角为10°,侧滑角为0°,用Fluent软件对模型进行仿真计算。再根据侧滑角公式推导要求,取传感器周角φ=0或π。如图 2所示的x轴上的传感器阵列,根据公式要求选取三个测量值一组,使用15种传感器组合,如表 1所示,对侧滑角进行计算。
Sensor groups | L2, R1,L3 | L3, R1,L4 | L1, R2,L3 | L1, L4,R2 | L3, R2,L4 |
| Number | 1 | 2 | 3 | 4 | 5 |
| Sensor groups | L1, L2,R3 | L1, L2,R4 | L1,L3,R4 | L2, L3,R4 | L1, R2,R3 |
| Number | 6 | 7 | 8 | 9 | 10 |
| Sensor groups | L2, R1,R3 | L2, L3,R3 | L3,R2,R1 | L2, L3,R1 | L1,R3,R1 |
| Number | 11 | 12 | 13 | 14 | 15 |
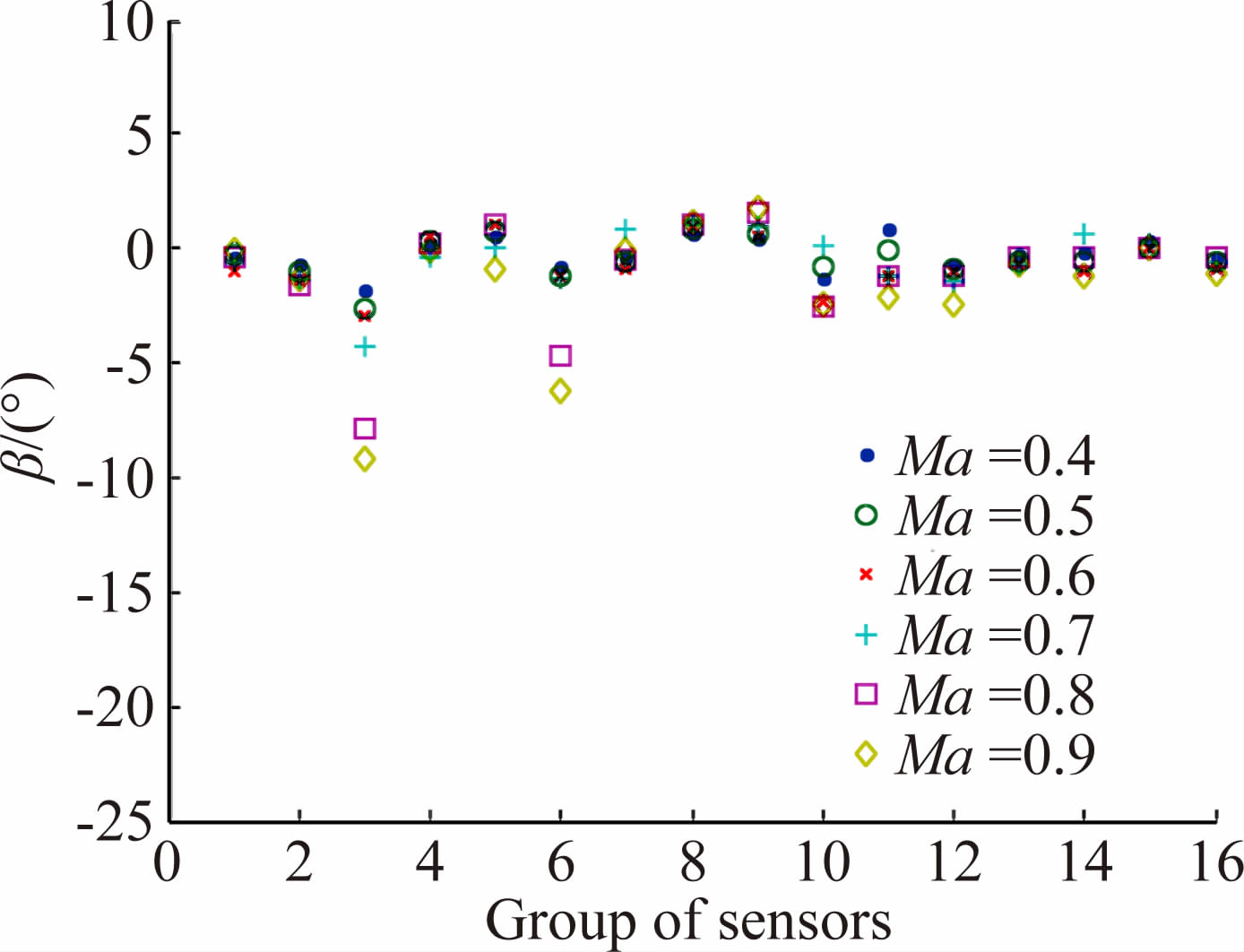
根据侧滑角的计算公式(23),得到其估计值,结果如图 7所示,不难看出,采用传感器组合2、5、8、9所得到的估计值偏离真实值较大,这些传感器组合被定义为不良组合。分析可知,这些组合都包含了标号为L3和L4或者L3和R4的传感器组合,即同组中同时含有两个较大气流入射角的传感器组合。从压缩性系数的校正局部放大图可知,锥角大于50°的传感器,其压缩性系数随着锥角的增加,压缩性系数逐渐减小,这导致了使用含有大锥角的传感器组合进行估计时,出现了明显的误差。此外,0.8、0.9Ma下的估计值依次出现相对略大的偏差,说明随着马赫数的增加,估计偏差略偏大。除去不良组合后的计算均值0.27°。
|
| 图 7 0°侧滑角仿真计算值 Fig. 7 Simulation resultat sideslip of 0° |
验证攻角表达式时,根据攻角公式(26)的推导要求,选取圆周角φ=$\frac{\pi }{2}$或$\frac{3\pi }{2}$的传感器进行求解,即图 2中y轴上的传感器,共采用了12种传感器组合,具体如表 2所示。
Sensor groups | U1,U2,D3 | U1, U4,D3 | U2, U4,D3 | U1,U2,D4 | U1,U3,D4 | U2, U3,D4 |
| Number | 1 | 2 | 3 | 4 | 5 | 6 |
| Sensor groups | D1, D2,U3 | D1,D3,U3 | D2,D3,U3 | D1,D2,U1 | D1,D3,U1 | D2,D3,U1 |
| Number | 7 | 8 | 9 | 10 | 11 | 12 |
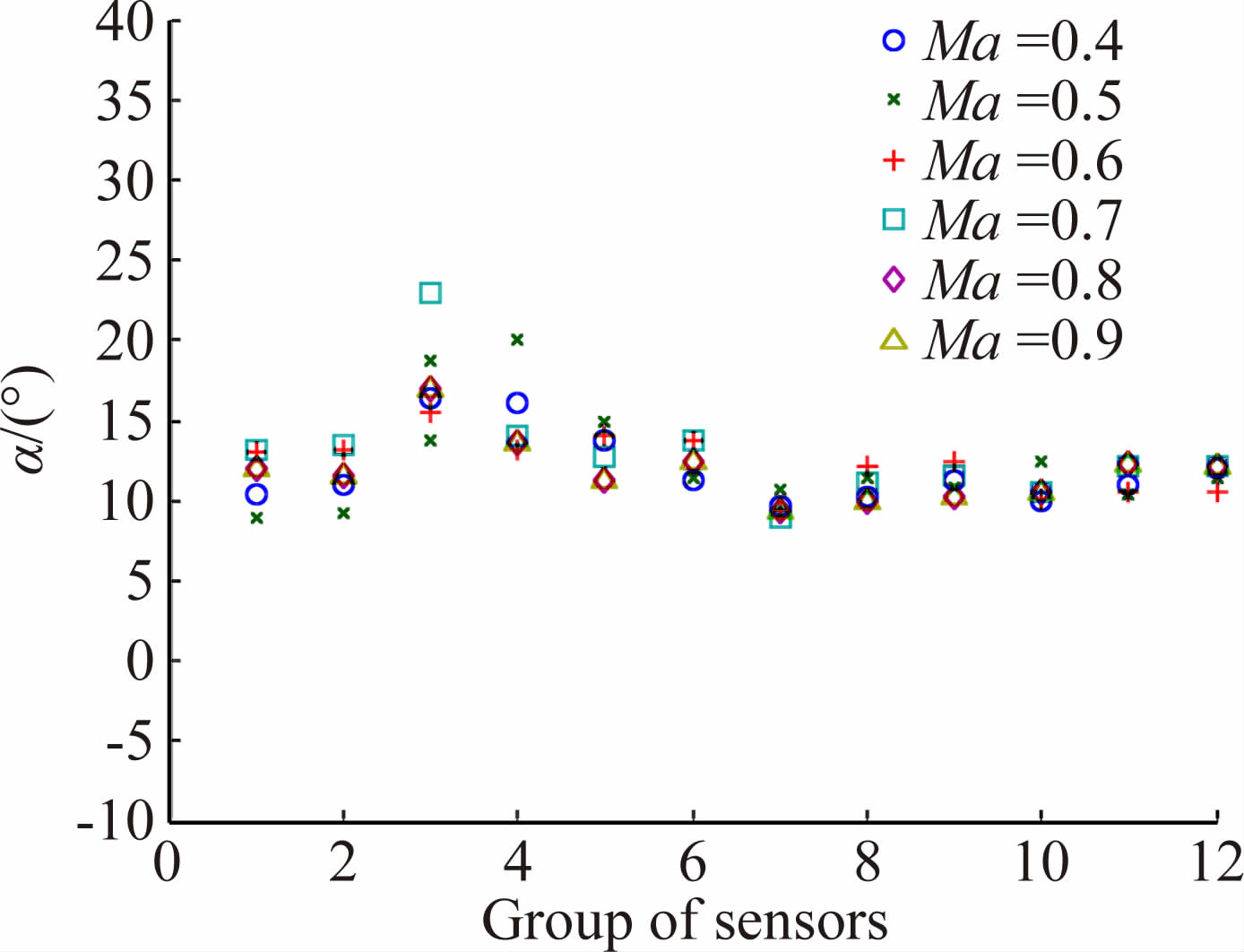
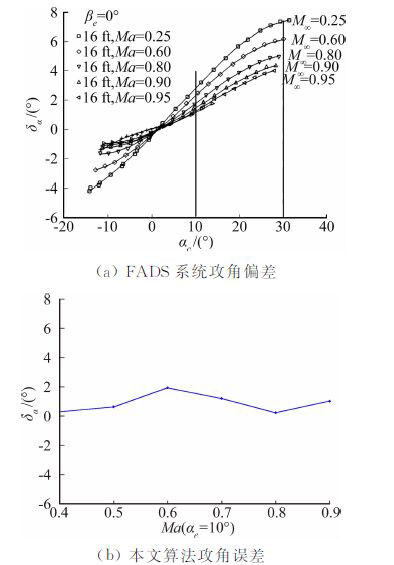
当攻角为10°时,通过仿真计算所得攻角的结果如图 8所示。其中,编号为3、4、5、6的传感器组合的估计结果存在较大偏差。因此,同样这些传感器组合被认为是不良组合。这与侧滑角的估计相似,它们都是包含了大锥角的传感器组合。除去以上不良传感器组合,其余组合在各马赫数下攻角的值如图 9所示。从图 9中可以看出,本文方法计算的攻角偏差均小于2°,它小于利用FADS系统计算的攻角偏差。
|
| 图 8 10°攻角时各组合仿真计算值 Fig. 8 Simulation result of all groups at angle of attack 10° |
|
| 图 9 攻角误差对比 Fig. 9 Comparison of attack error |
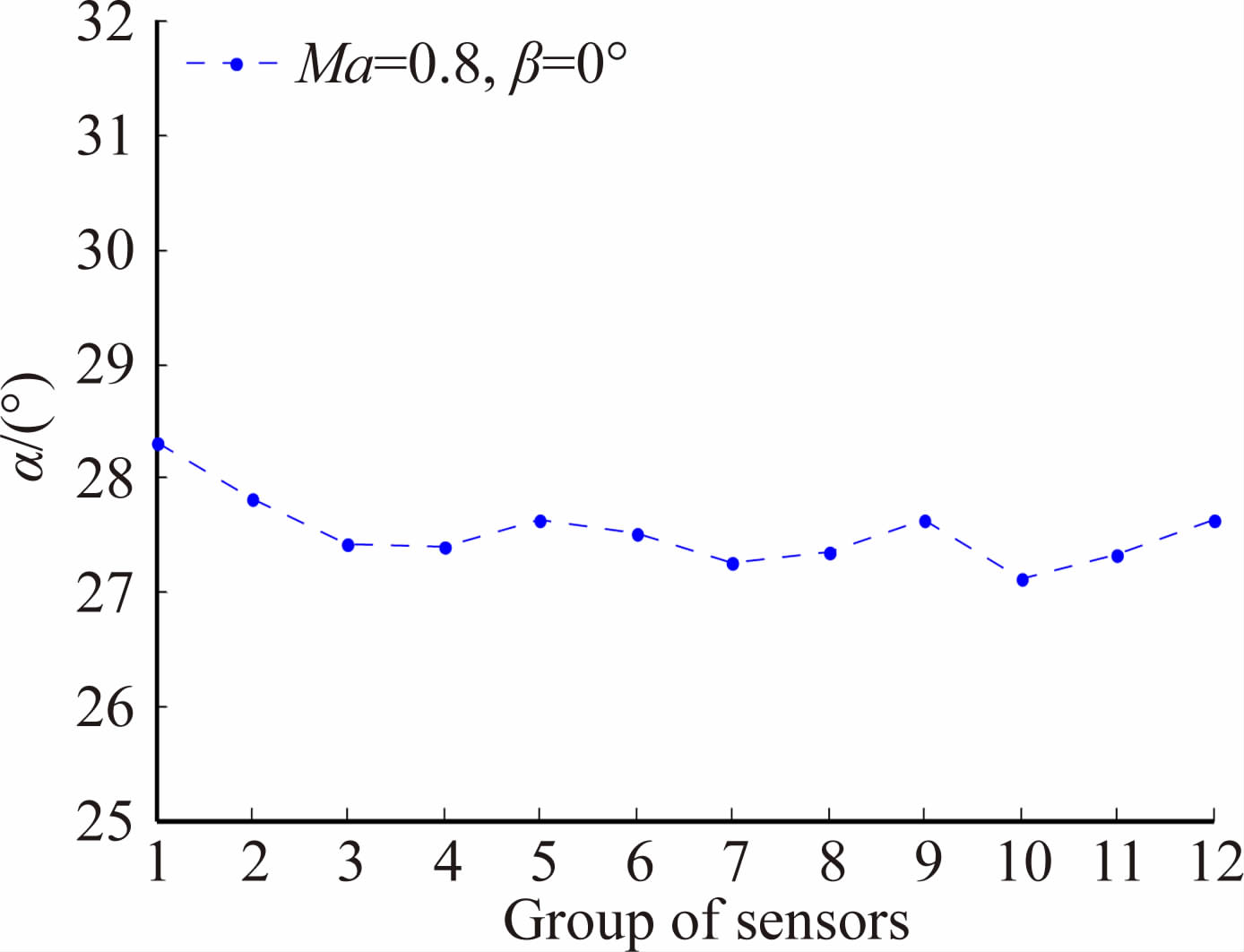
在较大攻角下,设定速度为0.8Ma,攻角、侧滑角分别为30°、0°,并将传感器重新分布在从0°到45°的锥角范围内,间隔5°,进行仿真并采样数据,通过各传感器组合进行仿真计算,其仿真结果如图 10所示。由于所有传感器的气流入射角均未超过45°,仿真结果并未出现明显波动,其计算结果的均值为27.5°,偏差为2.5°。而从图 10中可以看出FADS系统在30°攻角条件下其结果误差达到了5°,偏差明显大于本文方法。
|
| 图 10 30°攻角条件下仿真计算值 Fig. 10 Simulation result at angle of attack 30° |
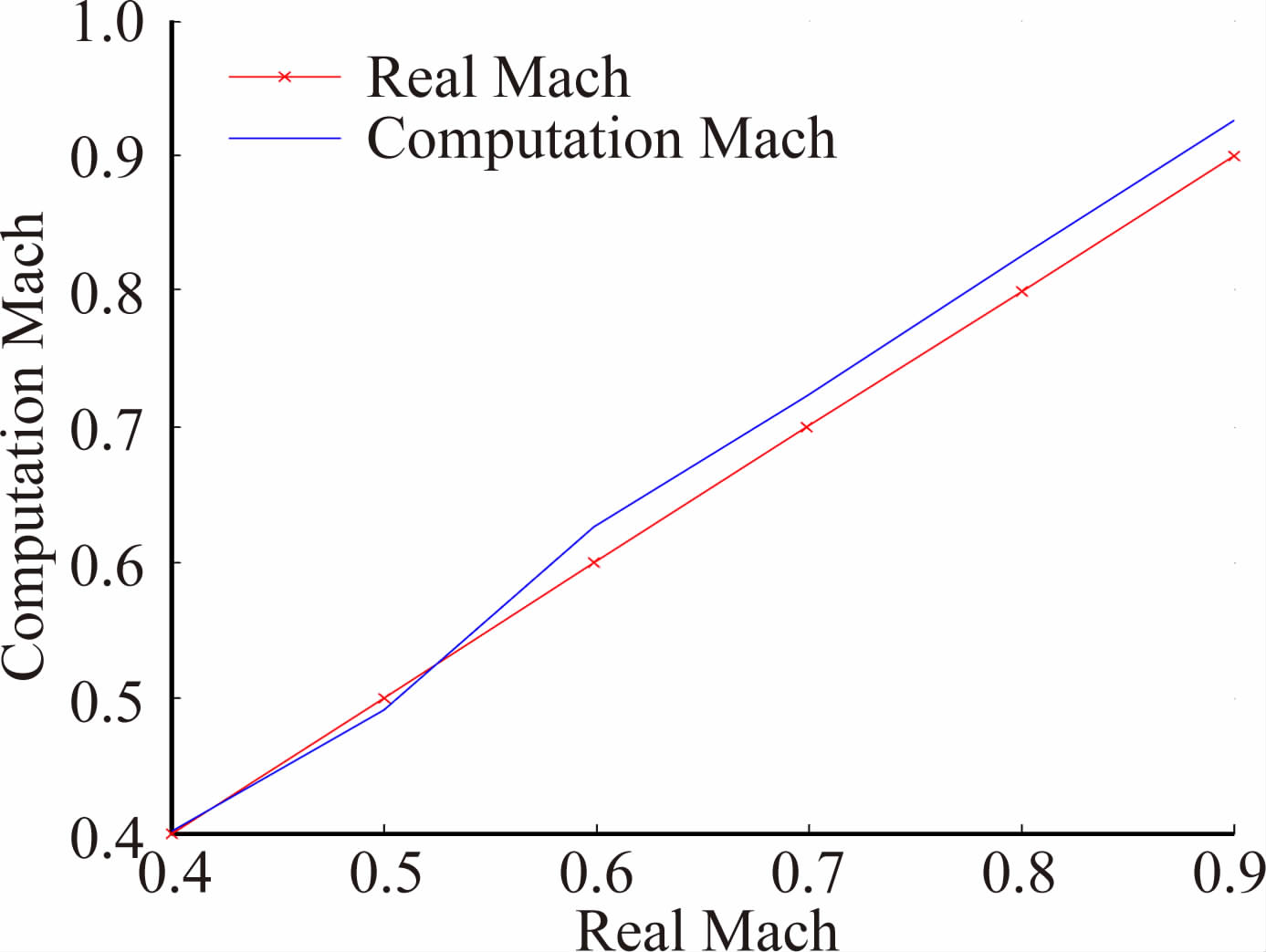
在攻角为10°、侧滑角为0°的条件下,图 11给出了利用本文算法求解的空速随马赫数Ma变化的曲线,其中菱形连线为真实空速曲线,叉形连线为计算所得的空速曲线。从图 11中看出,空速估计值十分接近其真实值,其平均误差小于2.2%,在从Ma=0.4到Ma=0.9范围内均有很好的估计。因为速度计算公式与气流入射角直接相关,因此气流入射角的精度决定了速度计算精度。由于速度计算式不需要求解动静压参数,因此避免了FADS系统中复杂的迭代算法,由攻角、侧滑角可直接计算获得,在解算速度上有着不可比拟的优势。
|
| 图 11 空速随马赫数变化曲线 Fig. 11 Flight speed variation by Mach numbers |
从计算结果可以看出基于气流速度模型下的攻角、侧滑角、速度公式很好地符合了仿真的设置条件,表明模型是可行的,更为重要的是计算速度上明显优于FADS系统不得不采用的迭代算法。但是模型还只是在理论上对大气参数做了估计,在实际应用时,模型受飞行器尺寸、声矢量传感器的安装等因素影响,其可靠性还需验证,同时模型的计算误差也要进行校正。
| [1] | Davis M C, Pahle J W, White J T, et al. Development of a flush air-data sensing system on a sharp-nosed vehicle for flight at Mach 3 to 8[R]. NASA TM 2000-209017, 2000. |
| [2] | Whitmore S A, Davis R J, Michael J F. In-flight demonstration of a real-time flush air-data sensing(RT-FADS) system[R]. NASA TM 104314, 1995:1-17. |
| [3] | Whitmore S A, Moes T R, Leondes C T. Failure detection and fault management techniques for flush air-data sensing system[R]. NASA TM 4335, 1992:1-19. |
| [4] | Whitmore S A, Moes T R. Measurement uncertainty and feasibility study of a flush air-data system for a hypersonic flight experiment[R]. NASA TM 4627, 1994:1-18. |
| [5] | Jost M, Schwegmann F, Kohler D T. Flush air data system an advanced air-data system for the aerospace industry[C]//AIAA 2004-5028. AIAA Guidance, Navigation, and control Conference and Exhibit. Rhode Island, 2004. |
| [6] | EllsworthJ C, Whitmore S A. Reentry air-data system for a sub-orbital spacecraft based on X-34 design[C]//AIAA 2007-1200. 45th AIAA Aerospace Science Meeting and Exhibit. Reno Nevada, 2007. |
| [7] | Baumann J P, Keener J W. X-43A flush airdata sensing system flight-test results[J]. Journal of Spacecraft and Rockets, 2010, 47(1):48-61. |
| [8] | Edward J Artz, Nicholas W Dona. NASA Orion flush air data sensing system feasibility determination and development[C]//AIAA 2014-1115. 52nd Aerospace Sciences Meeting. |
| [9] | Song X Y, Lu Y P. Research on design of pressure sensor of embedded airdata sensing system[J]. 2007, 27(5):8-10. (in Chinese)宋秀毅,陆宇平.嵌入式大气数据传感系统压力传感器设计研究[J].计测技术, 2007, 27(5):8-10. |
| [10] | Li Q C, Liu J F, Liu X, et al. Research on design of pressure sensor of embedded airdata sensing system[J]. Acta Aerodynamica Sinica, 2014, 32(3):360-363. (in Chinese).李其畅,刘劲帆,刘昕,等.嵌入式大气数据三点解算方法初步研究[J].空气动力学学报, 2014, 32(3):360-363. |
| [11] | Whitmore Stephen A, Tobert E Curry. Experimental characterization of the effects of pneumatic tubing on unsteady pressure measurement[R]. NASA TM-4171, 1990. |
| [12] | http://www.microflown-avisa.com/acoustic-localisation/AVS.html. |
| [13] | Wang L X, Tao J W. A new measuring air data algorithm[J]. Acta Metrologica Sinica, 2011, 32(1):44-48. (in Chinese)王立新,陶建武.一种新型的大气数据测量方法[J].计量学报, 2011, 32(1):44-48. |
| [14] | Chen C, Tao J W. Robust H∞ estimation of airspeed based on acoustic vector sensor array[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(2):361-370. (in Chinese)陈诚,陶建武.基于声矢量传感器阵列的鲁棒H∞空气流动速度估计算法[J].航空学报, 2013, 34(2):361-370. |
| [15] | Chen C, Tao J W, Zeng B. Estimation of airspeed in case of missing data[J]. Acta Electronica Sinca, 2014, 42(3):491-497. (in Chinese)陈诚,陶建武,曾宾.数据缺失情况下的空气流动速度估计算法[J].电子学报, 2014, 42(3):491-497. |
| [16] | Chen C, Tao J W, Zeng B. Estimation of airspeed based on acoustic vector sensor array[C]//11th International Conference on Signal Processing (ICSP 2012), 2012:307-310. |
| [17] | Zeng B, Tao J W, Yu F, et al. A new airspeed estimation method for supersonic flow[C]//2013 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC 2013), 2013:1268-1271. |
| [18] | Anderson J D. Fundamentals of aerodynamics[M]. New York:McGraw-Hill, 2011. |
| [19] | [KG1mm]Qian Y J. Aerodynamics[M]. Beijing:Beijing University Press, 2006. (in Chinese)钱翼稷.空气动力学[M].北京:北京航空航天大学出版社, 2006. |
| [20] | Ding Y, Wang Q. ANSYS ICEM CFD from trio to master[M]. Beijing:Tsinghua University Press, 2013. (in Chinese)丁源,王清. ANSYS ICEM CFD从入门到精通[M].北京:清华大学出版社, 2013. |
| [21] | Tang J P. FLUENT 14.0 super learning manual[M]. Beijing:Posts & Telecom Press, 2013. (in Chinese)唐家鹏. FLUENT 14.0超级学习手册[M].北京:人民邮电出版社, 2013. |


