2. 北京航天微系统研究所, 北京 100094;
3. 南京理工大学瞬态物理国家重点实验室, 江苏南京 210094
2. Beijing Aerospace Microsystems Institute, Beijing 100094, China;
3. National Key Laboratory of Transient Physics, Nanjing University of Science and Technology, Nanjing 210094, China
0 引 言
低雷诺数下翼型绕流在军用和民用方面都有着重要的应用[1, 2]。随着高空无人机、各种小型飞行器的不断发展,低雷诺数条件下高升阻比翼型的气动设计问题日益凸显,这些问题的解决都依赖于对低雷诺数下翼型边界层流动现象的深入研究。
低雷诺数条件下翼型表面边界层流动[1, 2, 3, 4]的抗逆压梯度能力较弱,容易产生流动分离,对翼型升阻比和飞行稳定性等产生严重影响。针对这种情况,人们一直在寻求有效控制流动的方法,试图通过改变飞行器边界层的流动结构,以达到消涡、减阻和提高飞行稳定性的目的。
边界层抽吸对抑制流动分离十分有效,特别是用于抑制低雷诺数下流动分离的抽吸控制成为近年来的研究热点[5, 6, 7, 8]。通过在分离点附近一定区域内等间距分布抽吸小孔,应用边界层抽吸吸除边界层内的低能流体,增强抵抗逆压梯度的能力,抑制流动分离,以达到增升减阻的目的。抽吸控制参数主要有抽吸系数、抽吸角度、抽吸孔径和抽吸孔间距等,文献[9]给出了上述单一参数对抽吸控制的影响规律。刘沛清等[10]开展了吹/吸气控制翼型表面分离流动的数值研究,探讨了射流位置、射流角度和射流速度比三个参数对层流分离泡控制的影响规律。
先前,这些控制参数范围的选取主要依赖于设计者的经验和直觉[11],因而很难给出最优解。控制结构中所考虑的设计参数越多,则越难以确定最优参数组合。对于单一参数的寻优,可以通过一系列计算得到其最优值,但是一组多参数的最优值则必须通过其它方法得到。随着计算机技术、计算流体力学和大量优化算法的迅速发展,可以通过数值模拟研究抽吸控制对于流动分离的控制效果,并与先进优化设计算法相结合,为抽吸控制的优化设计提供新技术途径。Carnarius[12]等针对NACA4412翼型分离流动,采用最速下降法和伴随方法对稳态吸气的抽吸角度进行了优化设计,取得了良好的设计效果,但是指出该优化算法的收敛性和计算时间依赖于所选择的加权因子。Li和Navon等[13]采用基于非稳态N-S方程的离散伴随优化方法,对圆柱尾迹内涡脱落的吹/吸气控制进行了优化。Zymaris[14, 15]等主要研究连续伴随优化方法,通过对湍流模型建立伴随方程,以提高梯度的敏感度,并在S形管道中对抑制流动分离的吹吸气喷口位置进行了优化。虽然基于梯度的优化方法应用比较广泛,但是需要求解梯度,且在控制参数增多时效率会显著降低[12]。伴随方法编程复杂、实现困难,甚至是求解伴随方程与求解流动方程所花费的CPU代价相当[15]。
遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索方法,它通过适应度函数值评估个体,并在此基础上进行遗传操作,具有较强的鲁棒性,因而可以应用于复杂系统的优化。目前,遗传算法多用于优化翼型气动外形[16, 17, 18]等被动控制,在主动控制优化设计中应用较少。Huang[19]等将改进的遗传算法与N-S方程求解直接耦合,对双喷口吹/吸气控制NACA0012翼型流动分离的参数进行了优化,但是Huang采用系数加权法求解兼顾升力和阻力的多目标问题,只能获得单个解,难以求出整个Pareto最优解,并且将遗传算法与流场求解直接耦合会带来很大的计算量。
另一方面,目前对于抽吸控制的研究多集中于气动性能[5, 6, 7, 10, 19]的分析,而没有考虑抽吸控制作为主动控制所需要的能量消耗问题。本文综合考虑这两方面的问题,将抽吸控制优化定义为一个多变量、多目标优化问题。首先建立了一个快速、有效的优化平台,采用RBF神经网络作为目标函数的代理模型,以减少求解气动力的计算量;通过均匀设计方法获得样本数据,用于训练RBF神经网络;在基本遗传算法的基础上,发展了单目标优化和Pareto多目标优化的遗传算法程序。然后,对于低雷诺数下NACA0012翼型附面层分离流动,应用该平台进行了以升阻比作为单目标的优化。最后采用Pareto多目标遗传算法求解兼顾升阻比和抽吸能耗的多目标问题。
1 优化流程 1.1 代理模型代理模型为RBF神经网络,该网络结构由Moody J和Darken C[20, 21]提出,是一种三层前向网络,能够以任意精度逼近任意连续函数。由于输入到输出的映射是非线性的,而隐含层空间到输出空间的映射是线性的,从而大大加快了学习速度并避免局部极小问题,径向基神经元模型结构图如图 1所示。图 1中,每一个输入被赋予一定的权值,与偏差求和后作为神经元传递函数的自变量,神经元的输出是传递函数的输出。神经元传递函数的输入是权值向量与输入向量之间的向量距离和偏差b的乘积。图 1中‖dist‖代表权值与输入向量的点积。
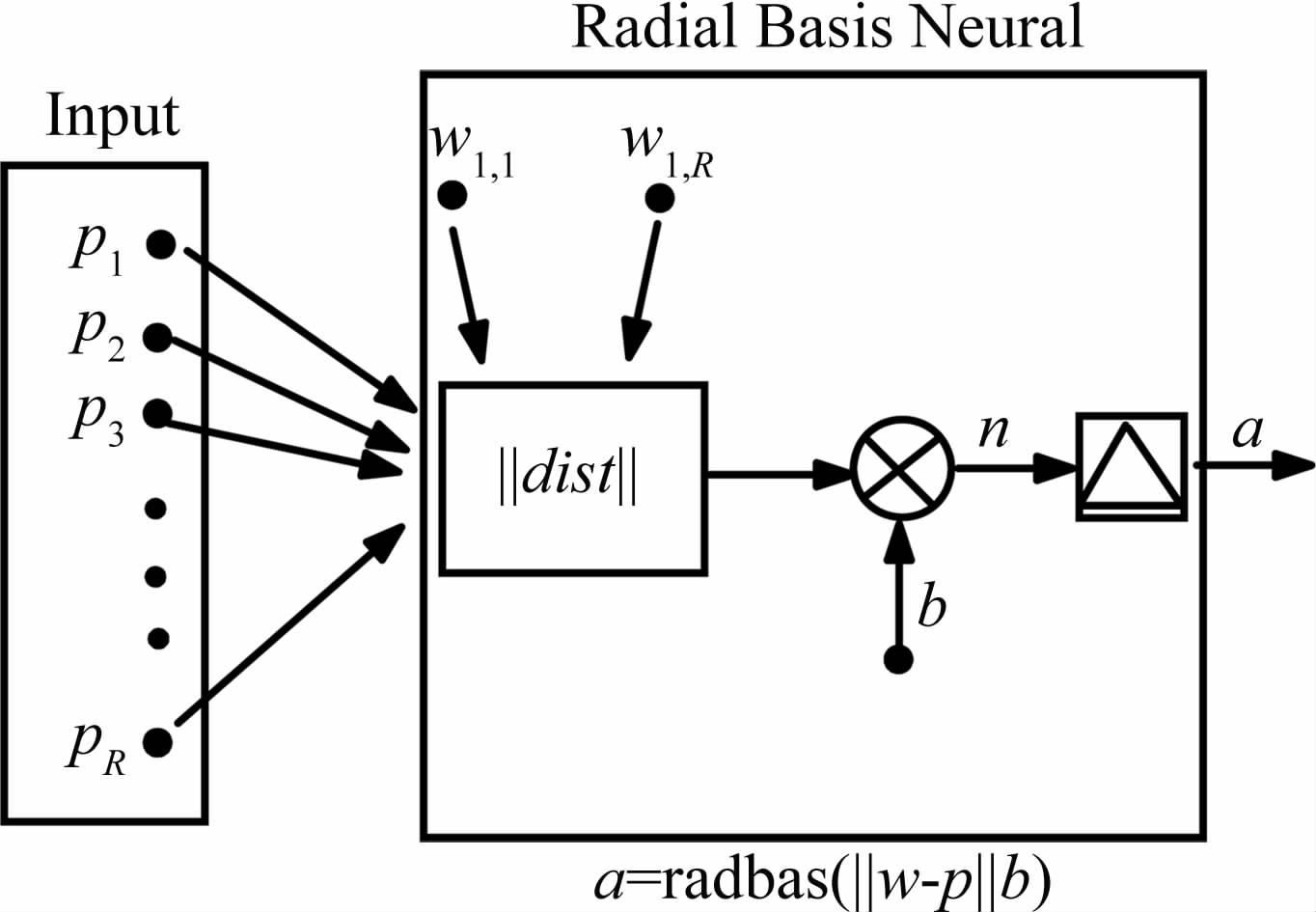
|
| 图 1 RBF网络结构 Fig. 1 Topology of RBF network |
遗传算法[22]是借鉴生物在自然环境中的遗传与进化机制而开发出的一种全局优化自适应概率搜索算法。它使用群体搜索技术,通过对当前群体施加选择、交叉、变异等一系列遗传操作,从而产生新一代的种群,并逐步使种群进化到包含或接近最优解的状态。遗传算法是一类具有较强鲁棒性的优化算法,特别是对一些大型、复杂非线性系统,它表现出比其它优化算法方法更加独特和优越的性能。
多目标优化设计问题是实际中常遇到的问题,其复杂特性极大限制了传统方法的鲁棒性和高效性,而且传统方法(比如加权法)在处理多目标最优化问题时通常将矢量目标函数转化为单个的标量目标函数,通常也只能获得单个解,难以求出整个Pareto最优解集。而遗传算法是基于群体搜索的,因此遗传算法是求解多目标优化问题Pareto最优解的一种有效手段。
本文采用实数编码、最优保存策略、均匀算术交叉和非均匀变异对基本遗传算法进行改进实现单目标优化算法。引入快速非支配排序算法、拥挤距离、拥挤距离比较算子和精英策略等技术[23],发展出Pareto多目标遗传算法。
1.3 优化框架的构建基于RBF神经网络和遗传算法的优化流程为:首先,采用均匀设计方法,选择在设计空间内均匀分布的样本点,从而保证网络的全局性。其次,采用高精度CFD求解器计算各样本的气动力及衡量抽吸能耗的品质因数(Figure of Merit,FOM),构建相应的RBF神经网络。最后,将训练好的RBF神经网络与遗传算法相结合,开展优化设计。上述优化流程如图 2所示。
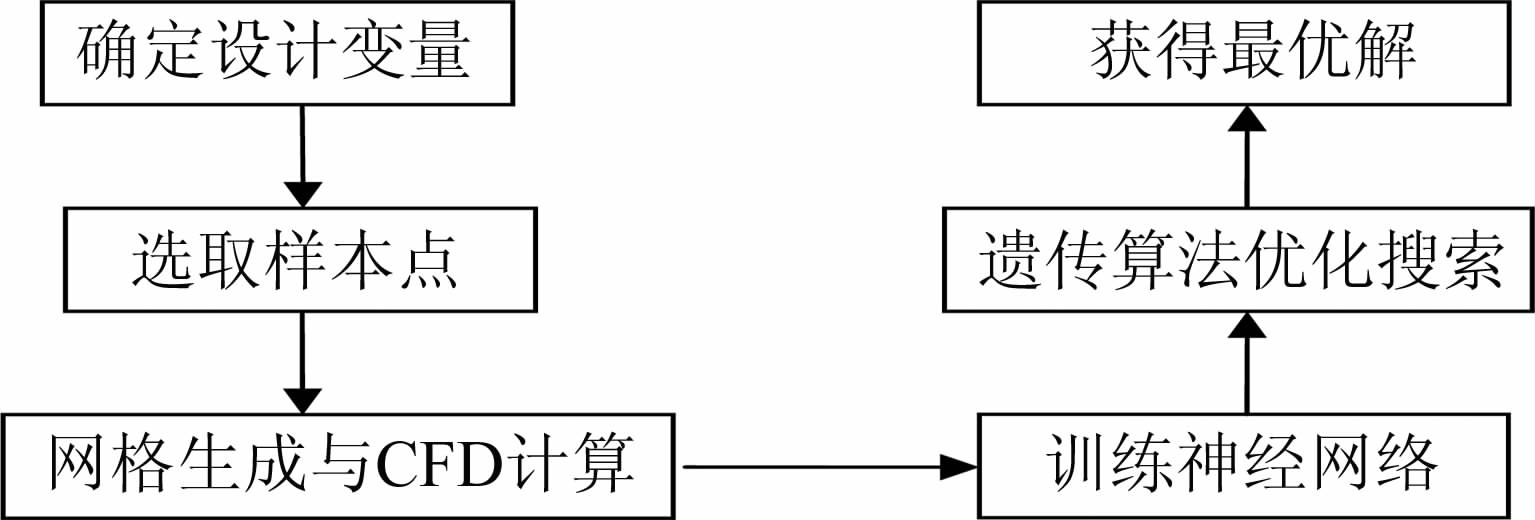
|
| 图 2 优化流程图 Fig. 2 Flow chart for optimization |
采用有限体积法对二维非定常Navier-Stokes控制方程进行离散。对流项采用AUSM+-up格式[24]进行离散求解,AUSM+-up是可以计算全速流动的格式,兼有Roe格式的间断高分辨率和van Leer格式的计算效率高的优点,同时它的数值耗散小,无需熵修正。采用三阶加权基本无振荡格式(Weighted Essentially Non-Oscillatory)[25]对流场变量进行重构以提高模拟精度。粘性通量采用二阶中心差分格式离散。时间推进采用具有二阶精度的双时间步长LU-SGS全隐式算法[26]。并采用当地时间步长和隐式残差光顺等措施加速收敛。
在低雷诺数流动中,不稳定的大尺度层流结构控制了低雷诺数分离泡的再附和涡的脱落,而湍流仅起到次要作用[2, 27]。并且Elimelech[28]通过对低雷诺数翼型流动的研究,证明层流模型足以求解低雷诺数下的流动结构。本文的计算也证明了这一点,故为了减小计算代价以便进行抽吸控制的优化,本文采用层流模型。
外边界采用远场边界条件。固壁采用无滑移边界条件。抽吸边界条件:给定抽吸速度大小和抽吸角度;密度由内部流场值一阶外推得到;压力通过伯努利方程求出。
2.2 基准状态与验证为了验算上述算法的正确性,计算模型采用NACA0012翼型,该翼型有着丰富的实验和数值模拟结果。采用椭圆方法生成“C”型网格,以翼型弦长c=1为特征长度。计算工况为Re=10000,Ma=0.2的低雷诺数流动,Ohtake等[29]通过实验研究得到NACA0012翼型在该低雷诺数下的非线性气动特性。本文首先计算该流动条件下绕NACA0012翼型流动,以对本文数值算法进行验证,同时将该结果作为流动控制的基准状态。为了准确模拟分离区流动,对NACA0012翼型上翼面后缘和尾迹区进行了加密。通过网格无关性检验,最终选取网格节点数为895×97,其中翼型表面分布了360个网格点。
图 3给出了计算得到的升力系数与实验结果的对比。由图 3可见,在小攻角流动下(α<7°)数值模拟结果与实验值吻合较好;而攻角为8°时,翼型表面流动分离加重,相对于小攻角状态来说,湍流比重逐渐加大,这是导致攻角为8°时出现较大误差的主要原因。图 4给出了α=6°的瞬时涡量分布。由图 4可知,低雷诺数下绕NACA0012翼型流动分离现象是一个非定常过程,翼型前缘涡与后缘涡周期性地产生和脱落,并在尾迹区形成涡街。
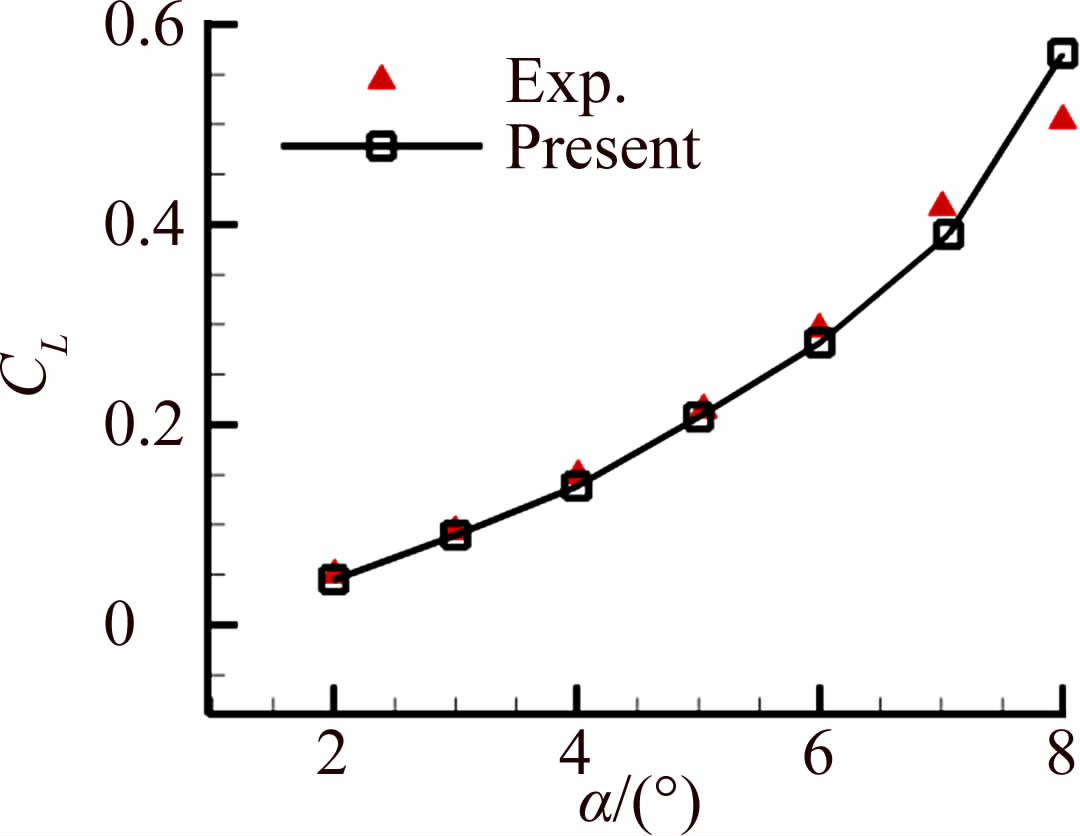
|
| 图 3 NACA0012翼型计算升力系数与实验结果对比图 Fig. 3 Comparison of the computational lift coefficients with the experimental results |
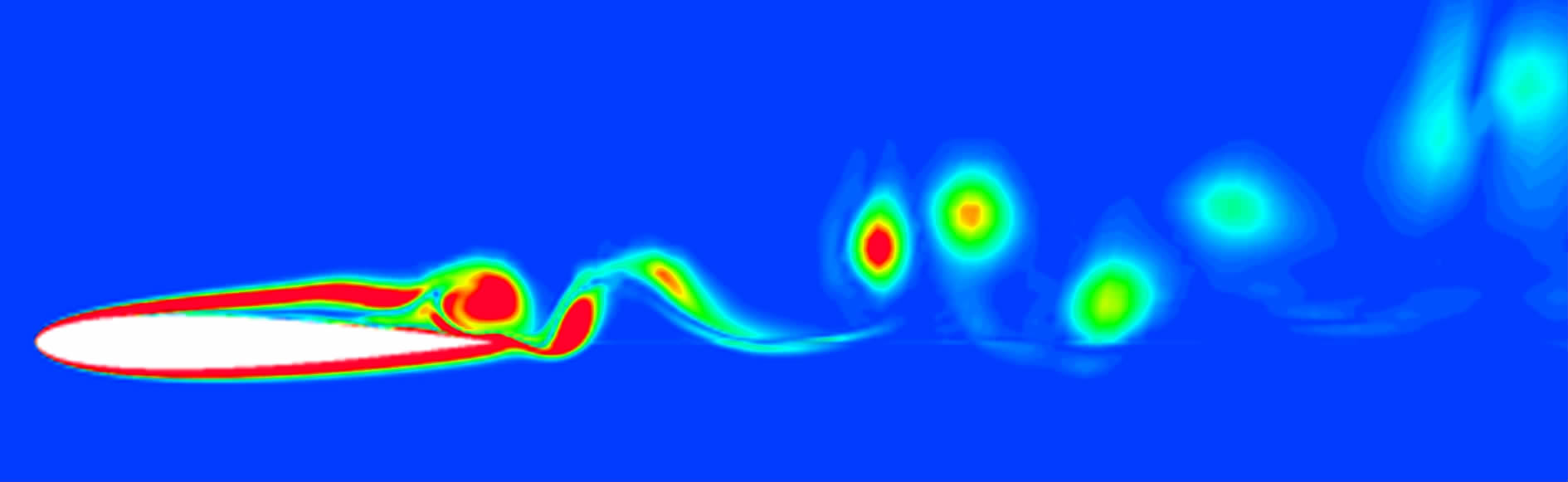
|
| 图 4 攻角为6°的瞬时涡量图 Fig. 4 Instantaneous vorticity distribution at the angle of attack of 6° |
综上所述,本文数值算法对于计算低雷诺数、小攻角下条件的翼型绕流具有良好的准确性,能够反映出流动中周期性涡脱落等非定常现象。
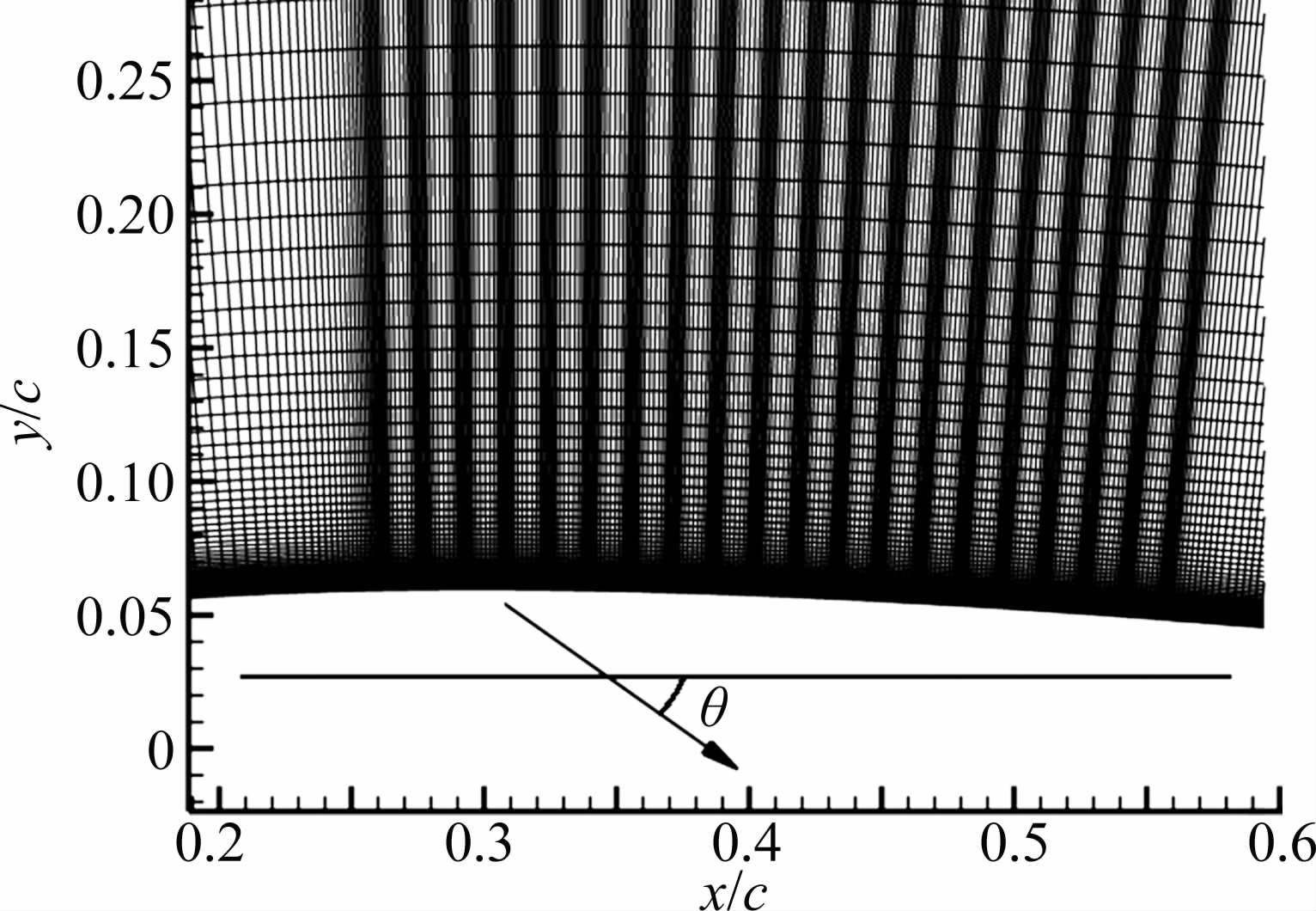
3 抽吸控制优化研究选取NACA0012翼型在攻角为6°的分离流动作为基准状态,其分离点大约位于0.245c处,通过抽吸控制吸除一部分低能流体,以延迟逆压梯度发生,达到抑制边界层分离、实现对翼型绕流控制的目的。在分离点之后,设置宽度为0.3c的抽吸区域,其起止点分别为0.26c~0.56c。由于孔径相对于弦长很小,为了精确模拟抽吸控制对流场的影响,对孔内部和周围网格进行加密,抽吸孔周围网格见图 5。θ是抽吸偏角,表示抽吸孔吸气方向与翼型弦线的夹角,当抽吸角度增加时,抽吸孔内吸气方向由顺主流方向吸入变到逆主流方向吸入。为了得到孔内多网格中心处的速度分布公式,假设孔内流动属于抛物线型的层流流动,在每个网格上对速度线型进行积分和平均运算,以满足有限体积法和质量守恒的要求,从而推导出一个统一形式的孔内多网格速度分布公式:
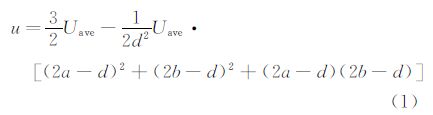
|
| 图 5 抽吸区域示意图 Fig. 5 Schematic of suction zone |
首先,定义一个无量纲的抽吸系数,它是衡量吸气效率的一个重要参数[30]:
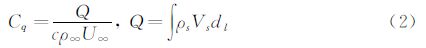
其次,为了对抽吸能耗进行评估,引入抽吸品质因数(FOM)[31]。认为抽吸所需的能量必须能够使吸气腔内的低压气体外排到环境中,即
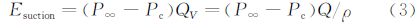
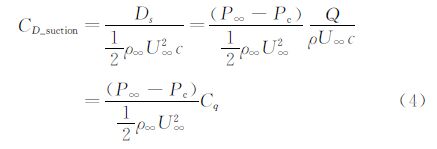
抽吸控制品质因数FOM可表示为:

选择四个参数作为抽吸控制优化的设计变量,分别是抽吸系数Cq、抽吸角度θ、抽吸孔径d和孔间距L,其中d和L是基于c的无量纲变量,并对每个变量的约束范围设置如下:
孔径: d∈[1×10-3c,4×10-3c];
孔间距: L∈[1×10-2c,2.5×10-2c];
抽吸角度:θ∈[30°,140°];
抽吸系数:Cq∈[2.5×10-3,1.2×10-2]。
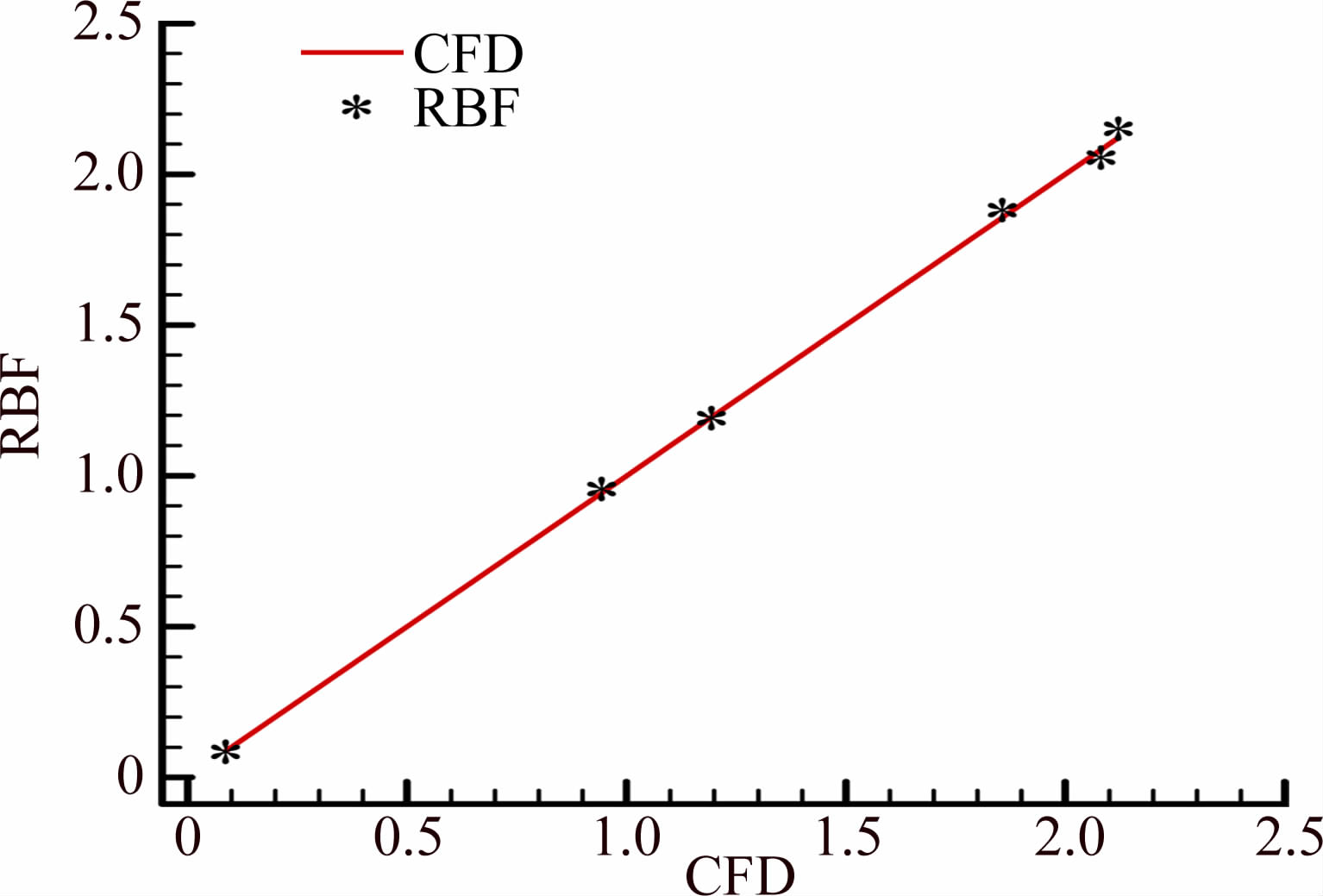
3.2 RBF神经网络模型的构建根据U12(122×42)混合均匀设计表采集12个样本点,针对每个样本中不同的孔径和孔间距,自动调用商用软件Gridgen中宏命令生成网格,然后进行CFD计算,得到其响应值(包括升阻比和FOM)。利用这些样本点信息对RBF神经网络模型进行训练,构造代理模型。通过U6*(64)均匀设计表获得6个测试样本,以检测代理模型精度。神经网络精度检测如图 6所示,最大误差为1.45%,具有较高的预测精度,可以在优化中使用该代理模型。
|
| 图 6 RBF神经网络精度检测 Fig. 6 Comparison of precision between neural network and CFD |
升阻比是衡量抽吸控制效果的一个重要参量。首先以获取最大升阻比为目标对抽吸控制进行了优化。该优化问题的数学模型可表述如下:
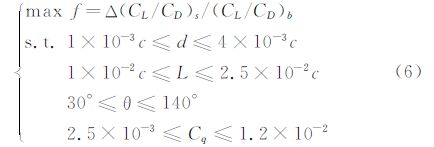
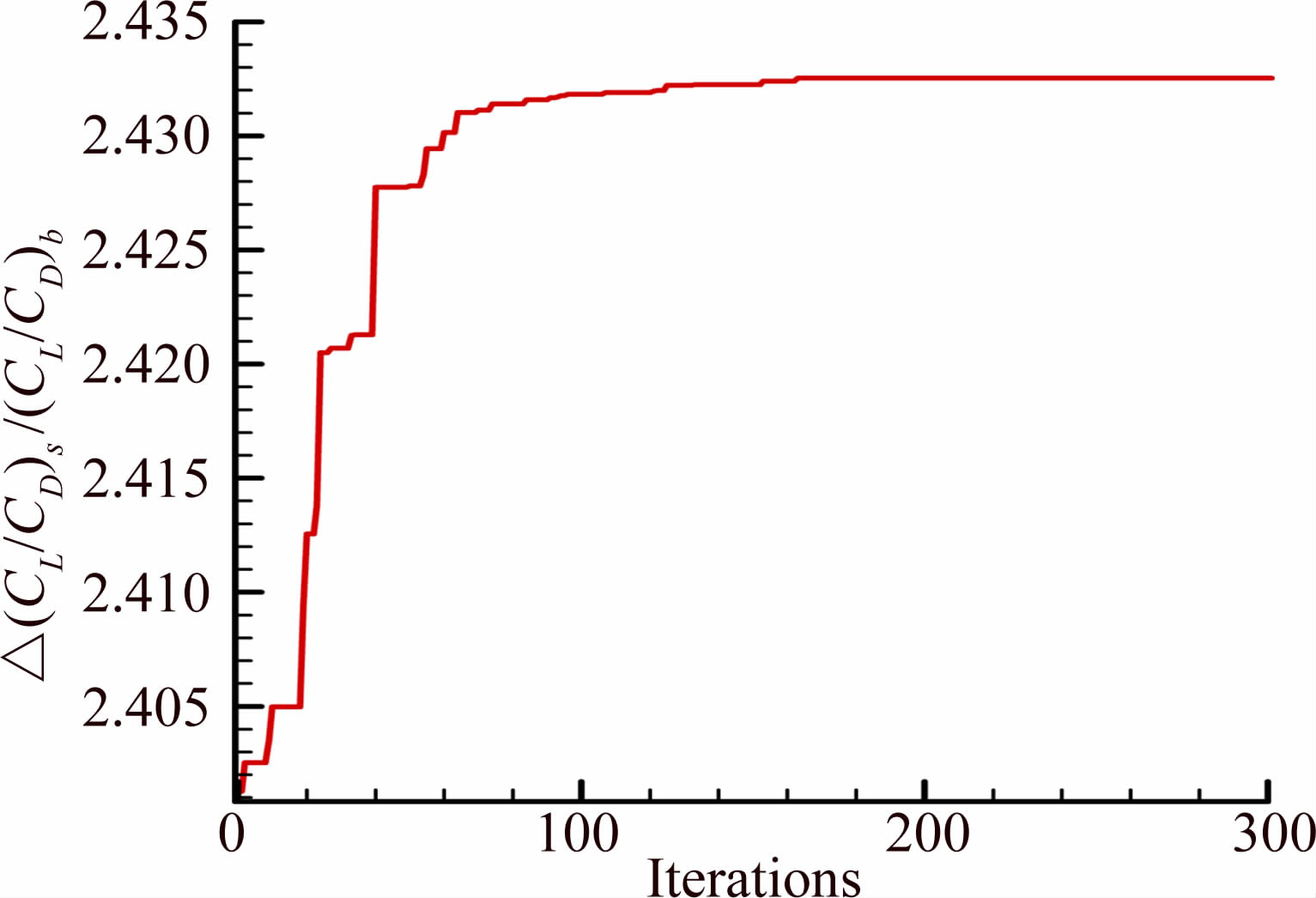
优化算法的控制参数设置为:初始种群数为30,进化代数为300,交叉概率为0.9,变异概率为0.05。其中,初始种群在初始化时,采用均匀设计法U30*(304)获得均匀分布的高质量初始种群,以加速收敛和防止早熟。在遗传算法搜索、迭代完成后,得到目标函数的收敛曲线,如图 7所示。在迭代次数为180次时遗传算法就已经收敛,寻找到最优解。
|
| 图 7 最佳适应度值的进化趋势 Fig. 7 Evolution of the optimal fitness |
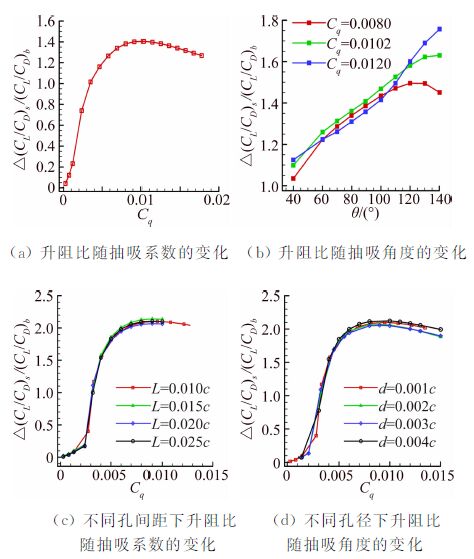
表 1给出了优化后的设计变量值、目标函数值及CFD计算值,通过比较发现本文优化平台具有相当的准确度。为了揭示优化过程的内在机制,图 8给出了各个抽吸控制参数分别对升阻比的影响规律。抽吸系数最优解为Cq=0.0113,接近其设计范围的最大值0.012。由图 8(a)可知,随抽吸系数的增加,升阻比先快速增加后缓慢减小,约在Cq=0.01附近出现极大值,表明抽吸系数的优化趋势是合理的。抽吸角度的最优值也是逼近设计范围的上界。图 8(b)为三个不同抽吸系数下的升阻比随抽吸角度的变化趋势,发现在较大抽吸系数下,升阻比随抽吸角度单调增加,这也表明优化解是服从这一规律的。图 8(c)和图 8(d)反映了升阻比变化规律受孔间距和孔径的影响不明显,且存在交互性影响,因此通过优化算法寻找孔间距和孔径的最优值不失为一种好办法。综上所述,虽然单参数寻优法可以使某些变化规律明确的参数找到其最佳值,但对于变化规律不明确的参数失效,而优化算法可以综合考虑四个参数对优化目标的影响,特别是存在交互性影响的参数,并得到相应的最优参数组合。
| Cq | θ | d | L | max(f ) | CFD | error |
| 0.0113 | 139.97° | 0.0014c | 0.0158c | 2.4328 | 2.39643 | 1.49% |
|
| 图 8 升阻比随抽吸参数的分布 Fig. 8 Distribution of lift-to-drag ratio with suction parameters |
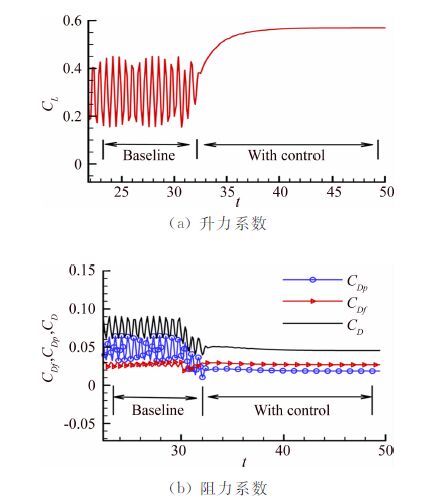
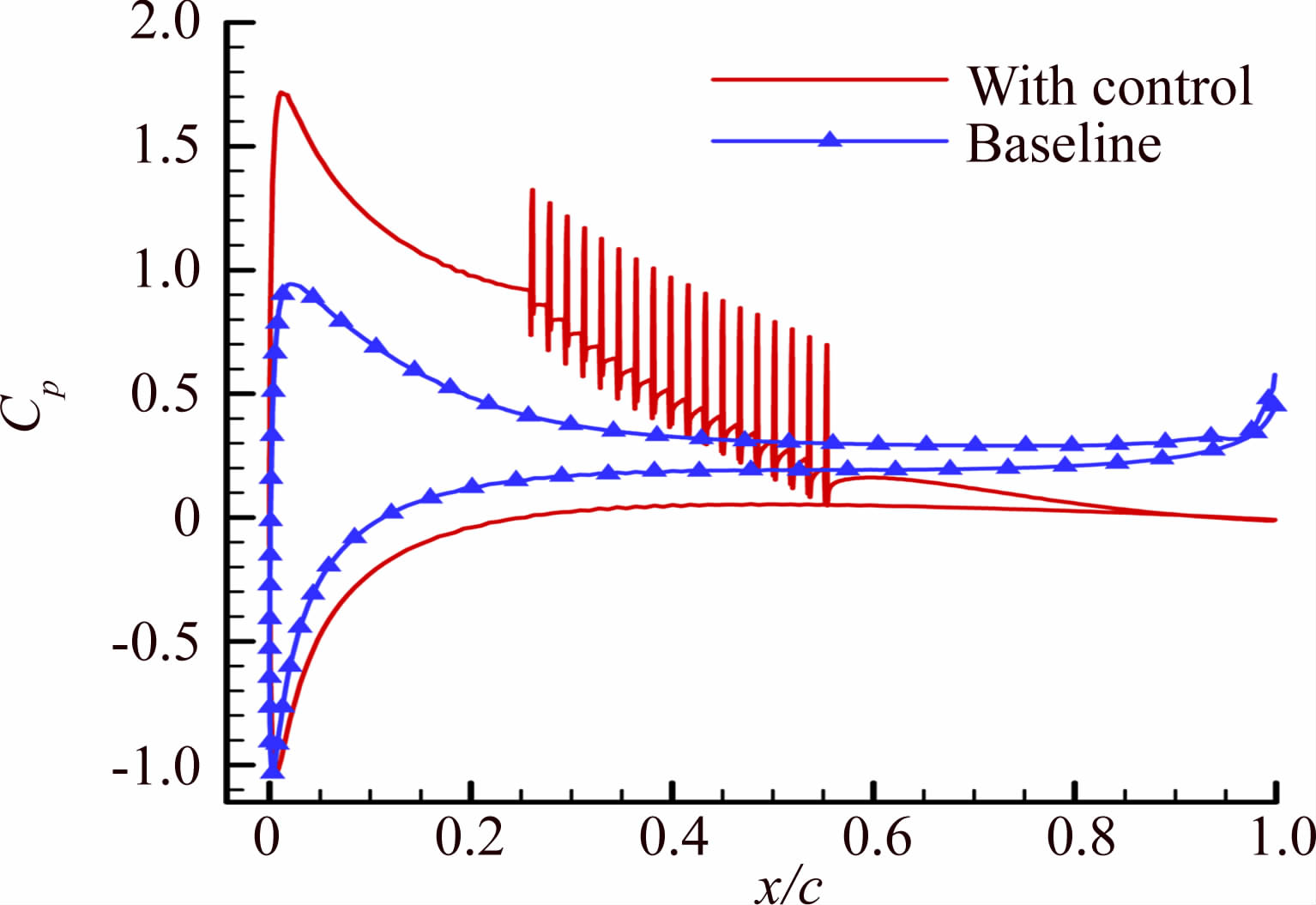
图 9给出了最优控制参数下的升阻力系数相对于基准状态的变化。升阻力系数曲线的变化可以明显地反映出增升减阻、消除非稳定波动的控制效果。图 10给出了最优控制下的压力系数,并与基准状态进行比较。可以发现,当升阻比达到最优解时,翼表面压力系数分布得到了明显改善,前缘附近的低压吸力峰值升高,下翼面压力系数获得了一定程度上的增加,这是导致升力系数获得增加的主要原因。图 9(b)显示在这组最优控制参数下,摩擦阻力系数的增加,使总阻力系数的减小幅度降低,根据式(5)可以得出FOM降低。另一方面,摩阻增加来源于抽吸控制下流向动量增加引起的壁面剪切应力增加,所以摩阻增加相当于消耗、抵消了一部分向控制系统注入的能量,导致整个控制系统的FOM减小,能效比降低。
|
| 图 9 最优控制下升阻力系数的变化 Fig. 9 Variations of lift and drag coefficients under the optimal control |
|
| 图 10 时均压力系数曲线对比图 Fig. 10 Comparison of time-averaged pressure coefficients |
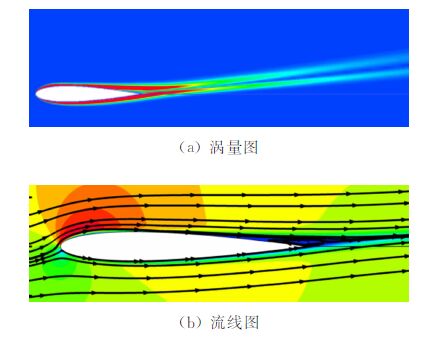
图 11给出了最优控制下涡量分布和流线图。相对于图 4中基准状态的涡量分布,脱落涡街已经完全消失,在尾迹区形成两条直线。流线图反映了翼型表面分离流动得到极大地抑制,流场变得稳定,只在翼型尾部形成一个稳定的回流区。
|
| 图 11 最优控制下涡量分布与流线图 Fig. 11 Distributions of vorticity and stream lines under the optimal control |
前面讨论的是单目标优化设计问题,而在实际应用中,经常遇到的是要求多个目标在给定区域上都尽可能好的优化问题,即多目标优化设计问题。抽吸控制属于主动流动控制,需要能量的注入和消耗,因此对抽吸控制效果的评价应当兼顾气动性能改善程度和抽吸能耗两个方面。
本节以升阻比和FOM两个指标作为多目标优化的目标函数。根据式(5)可知,FOM的最大化即为抽吸能耗的最小化。优化设计变量仍然是抽吸系数、抽吸角度、抽吸孔径和抽吸孔间距四个参数,多目标优化设计问题的数学模型可表述为:
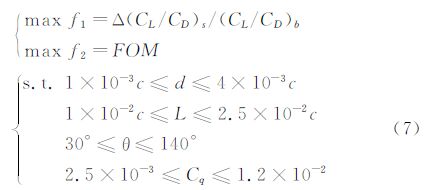
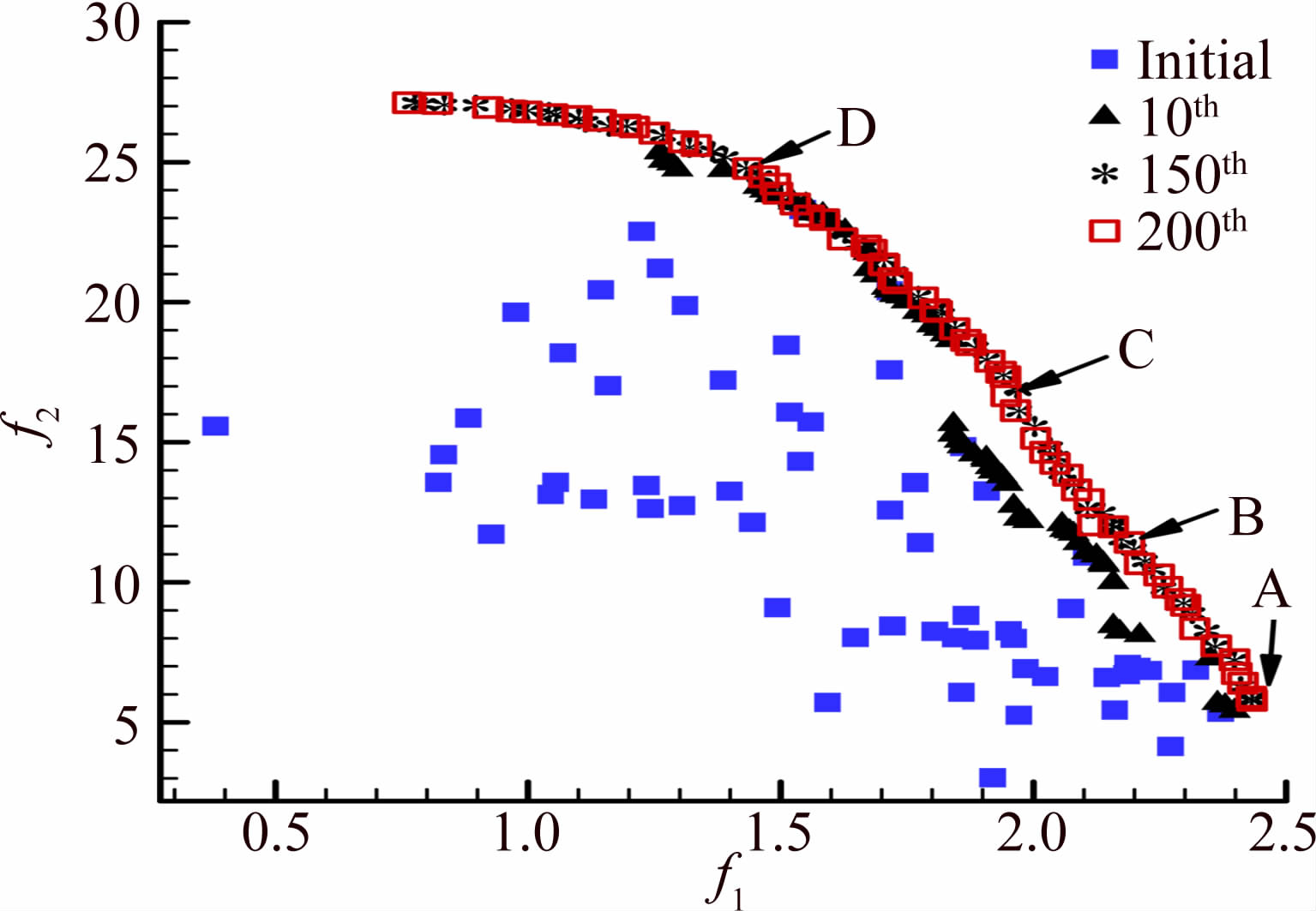
优化算法的控制参数设置为:初始种群数为60,进化代数为200,交叉概率为0.9,变异概率为0.05。图 12给出了进化过程中四代不同种群分布,发现经过10次迭代,种群解就很快逼近Pareto最优解;Pareto前沿分布是比较理想的,解的分布均匀性也得到保证,为设计者提供了一个可选的有效解数据库。在Pareto最优解集中,两个目标函数的分布范围为:0.7614≤f1≤2.4328,5.7867≤f2≤27.1211。
|
| 图 12 Pareto前沿分布 Fig. 12 Distribution of Pareto front |
另外,图 12中Pareto前沿反映出了f1和f2两个目标是矛盾的、冲突的,不可能同时达到各自的最大值。图 12中A点恰好是以升阻比为单目标优化的最优解所对应的状态,这表明单目标的优化设计只能得到局部解,而多目标优化设计可以给出一个完整的有效解集,在此基础上可以根据具体情况选择相应的控制参数组合。图 12中B、C、D三点为Pareto最优解集中的三个解,表 2给出这三个点的优化值及CFD计算值,通过分析可知,在合理选择抽吸角度、抽吸孔径和孔间距的前提下,只需较小的抽吸系数,或者较少的抽吸流量,就可以使升阻比获得明显增加,同时还能保持较高的FOM值,使整个控制系统的能效比维持较高水平。
| Cq | θ | d | L | Pareto Front | CFD | Error | ||||
| f1 | FOM | f1 | FOM | f1 | FOM | |||||
| B | 0.007858 | 139.761° | 0.0026c | 0.0156c | 2.1904 | 11.4212 | 2.1498 | 11.2537 | 1.88% | 1.49% |
| C | 0.006640 | 139.985° | 0.0040c | 0.0114c | 1.9460 | 16.6617 | 1.9082 | 16.3158 | 1.98% | 2.12% |
| D | 0.003915 | 120.727° | 0.0040c | 0.0158c | 1.4349 | 24.7702 | 1.4663 | 25.2514 | 2.14% | 1.91% |
本文采用RBF神经网络模型和遗传算法发展了单目标和Pareto多目标的优化平台,并将其应用到NACA0012翼型分离流动的抽吸控制优化设计研究中,获得了令人满意的最优解和Pareto最优解集。主要结论归纳如下:
(1) 通过升阻比的单目标优化,发现遗传算法很快收敛到最优解,得到了升阻比最优解及对应的抽吸控制参数组合。通过CFD验证了升阻比最优解的正确性,对最优抽吸控制参数组合进行了定性分析,证明优化算法在解空间中的搜索方向是合理的,显示了本文优化算法的有效性。
(2) 通过分析升阻比最优解下的流场特性,发现在最优抽吸控制下,翼表面压力系数分布发生了明显改变,上下压差增加,原流场中分离流动、非定常脱落涡得到了显著抑制。但是由于摩阻的增加,导致抽吸控制的FOM较小。
(3) 针对升阻比和FOM这一对相互矛盾的多目标问题,采用Pareto遗传算法进行优化搜索,得到了理想的、分布均匀的Pareto前沿分布,为设计者提供了一个有效解数据库,其中以升阻比为单目标的优化解仅是多目标Pareto最优解集中的一个端点。通过对Pareto最优解集中的三个典型解进行分析,发现在合理选择抽吸角度、抽吸孔径和孔间距的前提下,只需较小的抽吸系数,或者较少的抽吸流量,就可以使升阻比获得明显增加,同时还能保持较高的FOM值,使整个控制系统的能效比维持较高水平。
| [1] | Selig M S, Guglielmo J J. High-lift low Reynolds number airfoil design[J]. Journal of Aircraft. 1997, 34(1):72-79. |
| [2] | Lin J C M, PAULEY L L. Low Reynolds number separation on an airfoil[J]. AIAA Journal, 1996, 34(6):1570-1577 |
| [3] | Ran J H, Liu Z Q, Bai P. The effect of relative thickness to the dynamic aerodynamic characteristics about pitching airfoils[J]. Acta Aerodynamica Sinica, 2008, 26(2):178-185. (in Chinese)冉景洪,刘子强,白鹏.相对厚度对低雷诺数流动中翼型动态气动力特性的影响[J].空气动力学学报, 2008, 26(2):178-185. |
| [4] | Bai P, Cui E J, Zhou W J, et al. Numerical simulation of laminar separation bubble over 2D airfoil at low Reynolds number[J]. Acta Aerodynamica Sinica, 2006, 24(4):416-424. (in Chinese)白鹏,崔尔杰,周伟江,等.翼型低雷诺数层流分离泡数值研究[J].空气动力学学报, 2006, 24(4):416-424. |
| [5] | Bai P, Zhou W J, Wang Y Y. Investigation of effect of suction on delta wing separation flow at high angle-of-attack[J]. Acta Aeronautica et Astronautica Sinica, 1999, 20(5):393-398. (in Chinese)白鹏,周伟江,汪翼云.三角翼大攻角分离流开缝吸气效应研究[J].航空学报, 1999, 20(5):393-398. |
| [6] | Genc S M, Kaynak U. Control of flow separation and transition point over an airfoil at low Reynolds number using simultaneous blowing and suction[R]. AIAA 2009-3672. |
| [7] | Fournier G, Pellerin S, Phuoc L T. Control by suction of an incompressible flow past a circular cylinder:comparison between experimental and LES results[R]. AIAA 2004-2119. |
| [8] | Wahidi R, Bridges D H. Effects of distributed suction on an airfoil at low Reynolds number[R]. AIAA 2010-471. |
| [9] | Zhang W L, Tan J J, Chen Z H, et al. Effect of suction control on separation flow around an airfoil at low Reynolds numbers[J]. Acta Aeronautica et Astronautica Sinica, 2014,35(1):141-150. (in Chinese) doi:10.7527/S1000-6893.2013.0314.张旺龙,谭俊杰,陈志华,等.抽吸控制对低雷诺数下翼型分离流动的影响[J].航空学报, 2014,35(1):141-150. |
| [10] | Liu P Q, Ma L C, Qu Q L, et al. Numerical investigation of the laminar separation bubble control by blowing/suction on airfoil at low Re number[J]. Acta Aerodynamica Sinica, 2013,31(4):518-524. (in Chinese)刘沛清,马利川,屈秋林,等.低雷诺数下翼型层流分离泡及吹吸气控制数值模拟研究[J].空气动力学学报, 2013,31(4):518-524. |
| [11] | Jin D H, Gui X M. Aerodynamic design optimization of cascade airfoils based on multiobjective genetic algorithm[J]. Journal of Aerospace Power, 2007, 22(2):285-290. (in Chinese)金东海,桂幸民.应用多目标遗传算法的叶栅气动优化设计[J].航空动力学报, 2007,22(2):285-290. |
| [12] | Carnarius A, Gunther B, Thielte F. Numerical study of the optimization of separation control[R]. AIAA-2007-58. |
| [13] | Li Z J, Navon I M, Hussaini M Y, et al. Optimal control of cylinder wakes via suction and blowing[J]. Computers & Fluids, 2003, 32:149-171. |
| [14] | Zymaris A S, Papadimitriou D I, Giannakoglou K C, et al. Continuous adjoint approach to the Spalart-Allmaras turbulence model for incompressible flows[J]. Computers & Fluids, 2009, 38(8):1528-1538. |
| [15] | Zymaris A S, Papadimitriou D I, Giannakoglou K C, et al. Optimal location of suction or blowing jets using the continuous adjoint approach[C]. ECCOMAS CFD 2010, 5th European Conference on CFD, Lisbon, Portugal, 2010. |
| [16] | Duan Y H, Cai J S, Liu Q H. Surrogate model based optimization for airfoil desing[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(4):617-627. (in Chinese)段焰辉,蔡晋生,刘秋洪.基于代理模型方法的翼型优化设计[J].航空学报, 2011, 32(4):617-627. |
| [17] | Peigin S, Zhu Z Q, Epstein B. Applicable numerical optimization methods for aerodynamic design of civil aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(1):58-69, (in Chinese) doi:10.7527/S1000-6893.2013.0249. Peigin S,朱自强, Epstein B.可应用于民机空气动力设计中的数值优化方法[J].航空学报, 2014, 35(1):58-69. |
| [18] | Sonoda T, Yamaguchi Y, Arima T, et al. Advanced high turning compressor airfoils for low Reynolds number condition-Part Ⅰ:Design and Optimization[J]. ASME, 2004, 126:350-359. doi:10.1115/1.1737780. |
| [19] | Huang L. Optimization of blowing and suction control on NACA0012 airfoil using genetic algorithm with diversity control[D]. University of Kentucky, 2004. |
| [20] | Moody J, Darken C. Learning with the localized receptive fields[D]. Connectionist Models Summer School, Camegie Mellon Univ., 1988. |
| [21] | Moody J, Darken C. Fast learning in networks of locally-luned processing units[J]. Neural Computation, 1989,1(1):281-294. |
| [22] | Holland J H. Adaptation in natural and artificial systems[M]. Michigan:University of Michigan Press, 1975. |
| [23] | Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm:NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2):182-197. |
| [24] | Liou M S. A sequel to AUSM, Part Ⅱ:AUSM+-up for all speeds[J]. Journal of Computational Physics, 2006, 214:137-170. |
| [25] | Jiang G S, Shu C W. Efficient implementation of weighted ENO schemes[J]. Journal of Computational Physics, 1996, 126:202-228. |
| [26] | Rango S D, Zingg D W. Implicit Navier-Stokes computations of unsteady flows using subiteration methods[R]. AIAA 1996-2088. |
| [27] | Li J H, Li F. Low Reynolds number numerical simulation of inverse zimmerman wing[J]. Acta Aerodynamica Sinica, 2007, 25(2):220-225. (in Chinese)李建华,李锋.机翼低雷诺数流动的数值模拟[J].空气动力学学报, 2007,25(2):220-225. |
| [28] | Elimelech Y, Arieli R, Iosilevskii G. On the onset of transition at low Reynolds number flow over airfoils[R]. AIAA 2005-5311. |
| [29] | Ohtake T, Nakae Y, Motohashi Y. Nonlinearity of the aerodynamic characteristics of NACA0012 aerofoil at low Reynolds numbers[J]. Journal of the Japan Society for Aeronautical and Space Sciences, 2007, 55(644):439-445. |
| [30] | Saeed T I, Graham W R, Babinsky H, et al. Boundary-layer suction system design for application to a laminar flying wing aircraft[R]. AIAA 2010-4379. |
| [31] | Bridges D H. Early flight test and other boundary layer research at Mississippi State 1949-1960[J]. Journal of Aircraft, 2007, 44(5):1635-1652. |



