0 引 言
随着计算机技术的成熟,计算流体力学(CFD)[1, 2, 3, 4]这种数值模拟手段已被日渐广泛地用于旋翼气动特性的研究。基于N-S/Euler方程的CFD方法因为可以满足新型桨尖旋翼流场模拟的精度要求而成为当前开展旋翼气动性能研究的重要手段。但由于旋翼在旋转运动基础上叠加了复杂挥舞、变距运动,使得生成高质量的旋翼贴体网格较为困难。目前,主要采用嵌套网格方法来克服这一瓶颈。但由于在实际流场模拟时,旋翼相对于背景网格处于不断的运动当中,需要不断的更新两者之间的嵌套关系,这使得嵌套网格方法在必须保持高效的同时还应具有很好地鲁棒性。
当前嵌套网格方法主要由两个部分组成:一方面为计算单元与非计算单元属性的区分,即挖洞过程;另一方面为洞边界单元查找对应贡献单元的搜索过程。
对于前一种挖洞过程,国内外学者们发展了多种单元属性识别方法[5, 6, 7, 8]。LaBozzetta等[5]发展的射线法原理是对给任意点做射线,根据射线与已知边界交点的数量来判断该定点所属单元的属性。Slotnick等[6]提出的表面向量法先预设出洞边界,通过判断给定任意点与其最近交接面的面单元的关系来确定该定点所属单元的属性。上述两种方法均能较好地完成单元属性的区分,但在判断单元属性时均需要循环计算交接面上所有的面单元,这导致了计算效率较难提高。Meakin等人[7]提出的洞映射方法中借助辅助网格模拟目标网格的挖洞曲面,该方法效率和自动化程度较高。但由于结合了洞映射方法和目标射线法算法,提高了挖洞方法整体的复杂度,在实际应用中较为繁琐。国内也提出了多种洞边界识别方法[8, 9, 10],也获得了较好的效果。其中王博等人[11]吸收了洞映射法思想,提出的“透视图”挖洞方法能够适用于旋翼流场计算中的洞单元快速判断,但该方法形成的洞边界较难避开流场中的非线性区。
对于贡献单元搜索过程,Inverse-Map方法由于具有较高的计算效率而得到了广泛的运用。该方法构建覆盖于旋翼桨叶网格上的规则辅助网格(Inverse-Map),建立了桨叶网格与Inverse-Map单元索引之间的关系。对给定洞边界单元进行贡献单元搜索时,先在Inverse-Map上查找出可能的搜索范围,从而缩小了搜索范围。但在实际执行过程中,搜索效率取决于Inverse-Map相对于桨叶网格的分辨率。由于桨叶贴体网格在靠近物面处网格尺寸较小且实际桨叶具有复杂构型的特点,为了提高贡献单元的搜寻效率,需要建立高分辨率的Inverse-Map,这将会明显提高计算机内存的消耗和降低CFD的计算效率。此外,由于Inverse-Map是与桨叶固连,对弹性桨叶的模拟适应性较低,需在每次桨叶变形后重新生成。上述这些不足,限制了该方法的通用性和效率。
针对上述方法中的不足,本文分别对嵌套网格中的挖洞方法和贡献单元搜索方法进行改进,建立了一套新的预定边界运动嵌套网格方法。在挖洞方法中,引入了新的预定边界嵌套策略,并吸收“透视图”法的思想,发展了一套新的“逆向边界”挖洞方法。相对于常规嵌套网格方法中用于寻找覆盖于给定点在曲线网格上贡献单元的“Inverse-Map方法”,提出了可直接进行贡献单元搜寻的“Local Direct-Map”。最后,采用提出的预定边界嵌套网格方法对不同旋翼算例进行了数值模拟,验证了该方法的有效性。
1 “预定边界”运动嵌套网格方法提出的“预定边界”运动嵌套网格方法主要包括“逆向边界”挖洞方法和“Local Direct-Map”贡献单元搜寻方法。
1.1 “逆向边界”挖洞方法“逆向边界”挖洞方法主要包括两部分:设定预定边界和标记洞单元。
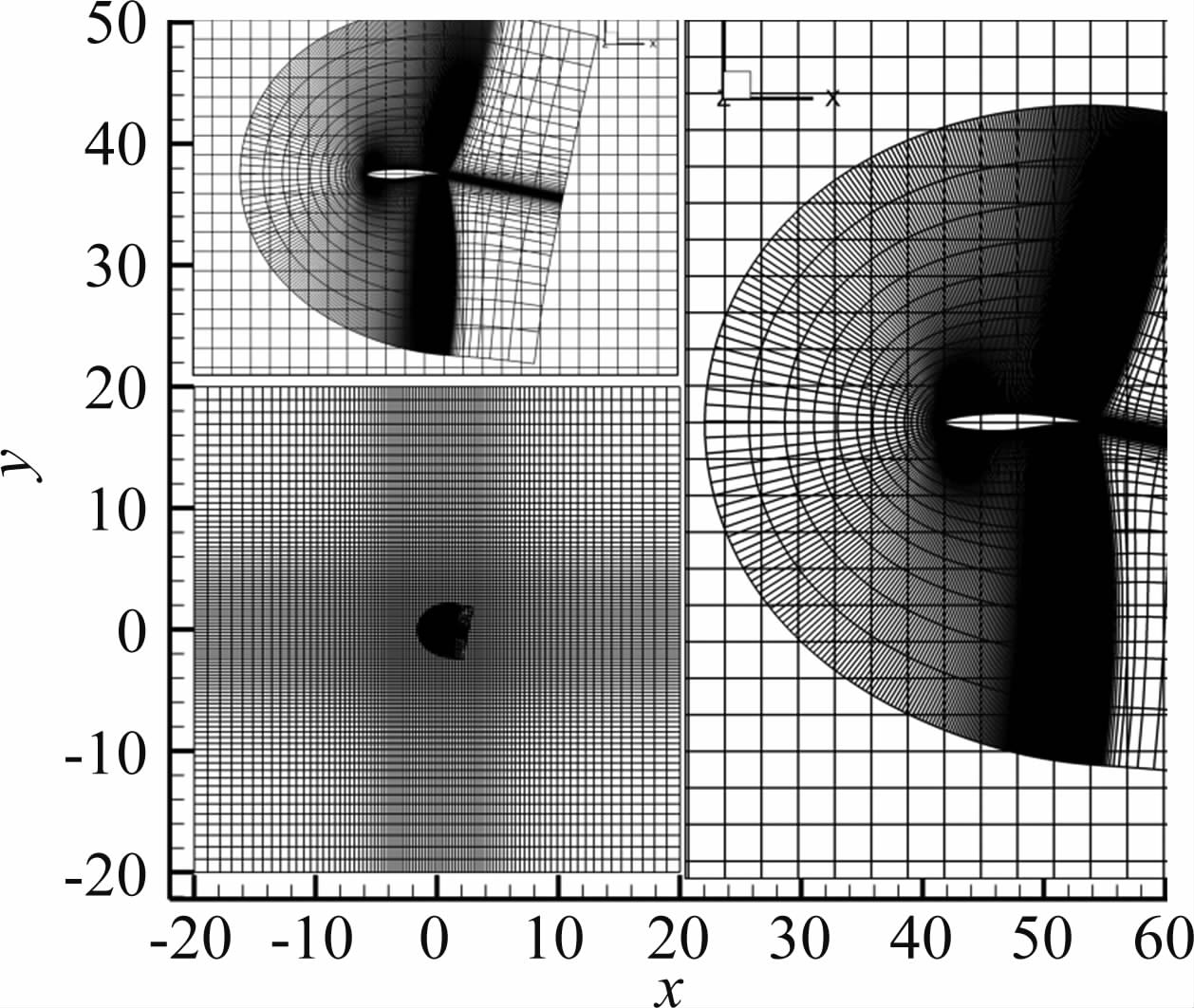
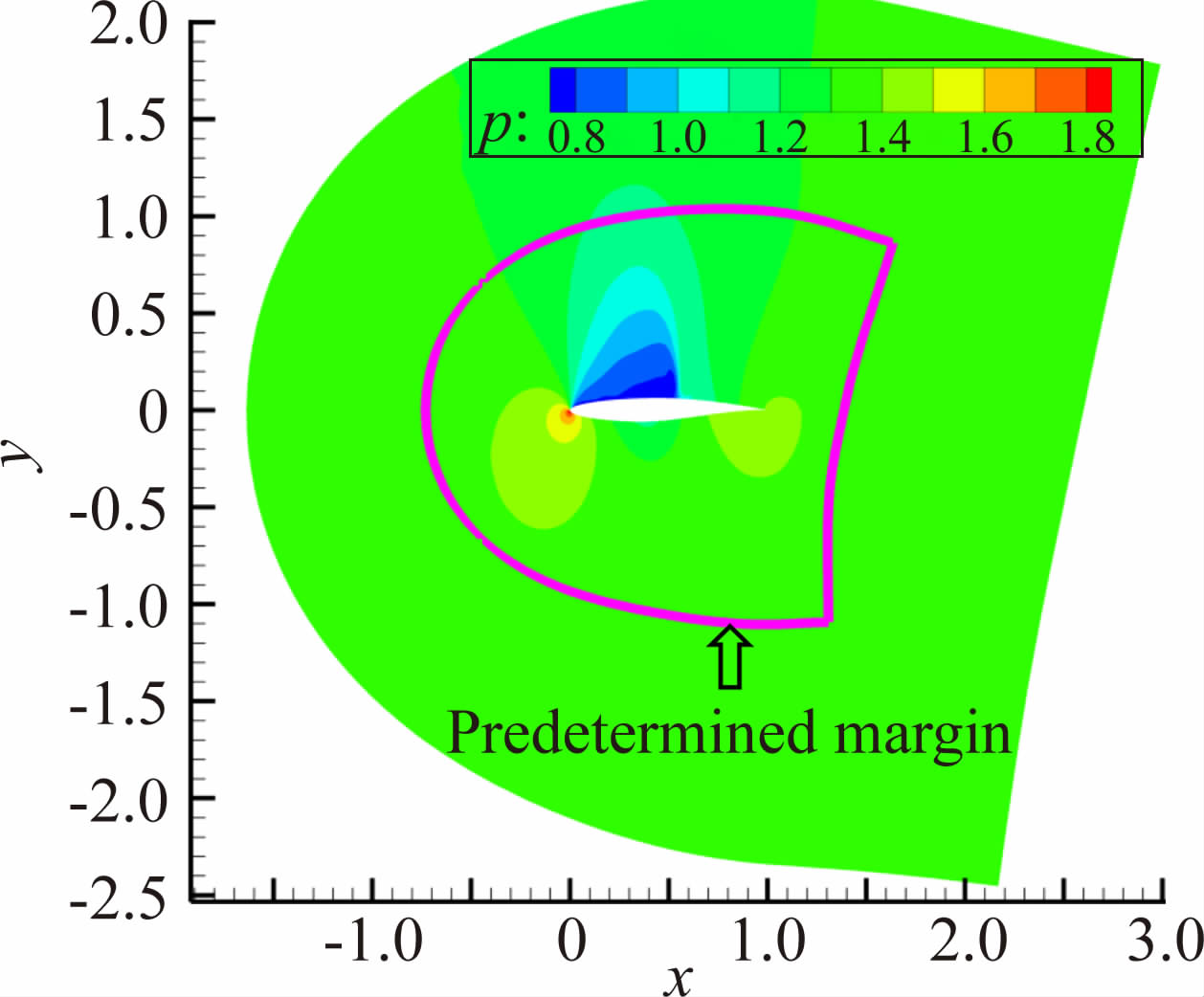
首先,将预定边界作为标记洞边界单元的依据,其选取原则就是保证嵌套网格间的信息传递在线性流动区域进行。因此,选取的边界应该在离开翼面附近的非线性区(如激波、气流分离区等)基础上,尽量离翼面较近且距离保持基本一致。实际模拟中该边界随着模拟状态的不同会发生调整。图 1给出了二维嵌套网格组成系统示意图,图 2给出了预定边界示意图。从图中可以看出本文提出的边界设定方法能很好地避开流场中的非线性区。
|
| 图 1 二维嵌套网格示意图 Fig. 1 Schematic of 2-D embedded grid |
|
| 图 2 预定边界示意图 Fig. 2 Schematic of predetermined boundary |
然后,对传统的“透视图法”进行改进,基本原理就是遍历所建立封闭曲面上的网格点,并搜索其在背景网格中对应的单元,该单元设定为背景网格的洞边界单元,并在搜索过程中记录洞边界单元对应的贡献单元的搜索范围,用以形成“Local Direct-Map”。以二维翼型网格为例,翼型网格尺寸M×N别,背景笛卡尔网格尺寸为P×Q(M、N、P、Q分为计算坐标方向上的单元数),建立用于存放洞边界单元序号和贡献单元搜索范围的数组DONER(M+2N,6),背景网格属性数组MARK(P,Q),初值设定为内场值1。“逆向边界”法基本步骤如下:
(1) 在背景网格上建立以x方向为基底的整数数组TOP(P,2),TOP(P,1)、TOP(P,2)分别存放该方向的上下限,数组初始化为0。
(2) 循环封闭曲面上的网格点,对曲面上任一网格点G坐标计算其所在背景单元的序号(p,q)(p、q分别为对应计算坐标下的坐标)。设定该单元为洞边界单元,对应有MARK(p,q)=2,对洞边界单元进行编号并将计算坐标和对应贡献单元搜索范围存放入DONER中。
(3) 在上述两步基础上,根据标出的洞边界单元进行洞单元识别;对所有MARK(p,q)=2的单元,作运算确定出洞边界单元范围:
a) 当TOP(p,1)=0或TOP(p,1)>q,有TOP(p,1)=q;
b) 当TOP(p,2)<q,有TOP(p,2)=q;
在上述过程完成后,对所有背景网格中进行:
c) 当TOP(p,1)≤q≤TOP(p,2)时,有MARK(p,q)=0;
d) 根据DONER信息还原洞边界单元。
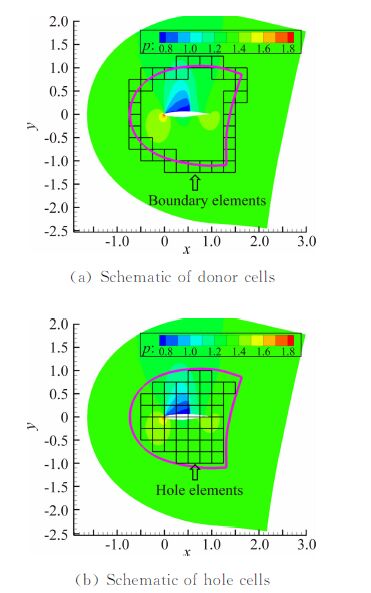
图 3给出了二维网格上采用上述的“逆向边界”法得出的预定洞边界单元和洞单元。从图 3中可以看出得到的洞边界单元很好地包裹了预定洞边界,并且洞单元均位于预定洞边界之内。
|
| 图 3 二维网格新“透视图”方法嵌套示意图 Fig. 3 Schematic of the new Top-Map in 2-D embedded grid |
提出的“逆向边界”法在进行挖洞时,已经预先对不同的桨叶限定了封闭曲面,从而贡献单元的搜索插值和洞单元的形成相对独立,为高性能并行计算提供了基础。此外,由于桨叶在运动过程中可能会出现桨叶表面网格点的间距比所投影的背景网格间距大的情况,此时可能会出现洞不连续的现象。因此,进行封闭曲面在背景网格上呈现时,充分考虑桨叶网格单元与背景网格单元的比例关系,需在相应的必要位置对桨叶表面网格适当加密以保证洞的连续性。
1.2 “Local Direct-Map”贡献单元搜寻方法Inverse-Map法是目前进行洞边界单元搜索贡献单元时的常用方法。该方法的原理就是通过一套规则的网格来包围所需要进行嵌套的网格,从而形成一张规则的可用于贡献单元搜索的地图。与真实的地图查找类似,找到准确位置的效率取决于地图的分辨率,即受到所建立的Inverse-Map精度的限制。而高精度的Inverse-Map会受到计算机内存和其对应网格分布特性的限制。因此,为更快捷、准确地进行旋翼洞边界单元的贡献单元搜索,提出了新的“Local Direct-Map”方法。
针对提出的“预定边界”的嵌套网格方法的特点,洞边界单元可以通过“预定边界”直接设定出位置。由定义可以得出背景网格的洞边界单元定位于“预定边界”附近,所以只需建立洞边界单元所对应的局部搜索范围就能完成贡献单元的搜索。以二维为例,具体算法如下:对于洞边界单元序列上任意一个单元H,DONER(H,3)用于存放桨叶网格上对应的M方向(沿翼型弦向)序号的下限,DONER(H,4) 用于存放桨叶网格上对应的M方向序号的上限,DONER(H,5) 用于存放桨叶网格上对应的N方向(沿翼型法向)序号的下限,DONER(H,6) 用于存放桨叶网格上对应的N方向序号的上限。对于洞边界单元H的贡献单元的搜索只需根据自身DONER(H,3:6)存放的范围进行搜索,该搜索过程可合并在上文中介绍的“预定边界”挖洞方法中进行,进一步提高了贡献单元的搜寻效率。
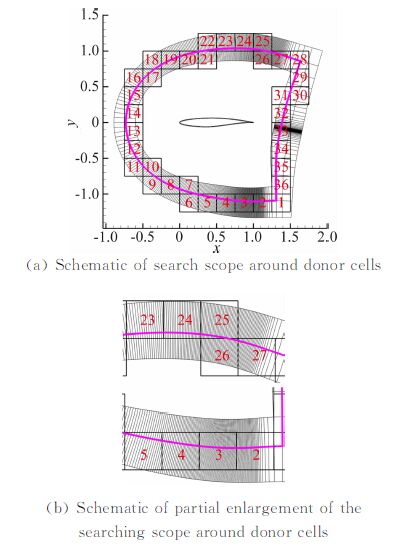
图 4给出了二维网格贡献单元搜索示意图。从图 4中可以看出大部分洞边界单元与翼型网格匹配得较好。在局部放大图中可以看出有些洞边界单元所对应的可能的贡献单元较多,也就是所需要检索的范围较大,因此这里根据结构网格的拓扑关系,采用二分法进行二维搜索进一步提高了查找效率。
|
| 图 4 二维网格贡献单元搜索范围示意图 Fig. 4 Schematic of searching scope around donor cells in 2-D |
根据提出的LDP方法原理,可以很明显地得出,当考虑桨叶变形时,由于围绕桨叶的网格单元在计算坐标上的拓扑关系保持不变,该方法仍能很好地适用且不用做任何特殊设定。当用于非结构网格类型搜索时,由于其网格本身具有的特殊单元拓扑关系,LDP方法可以进一步简化成只需存放与洞边界单元有关的少数网格单元计算坐标系下的位置就可以满足上述目标。
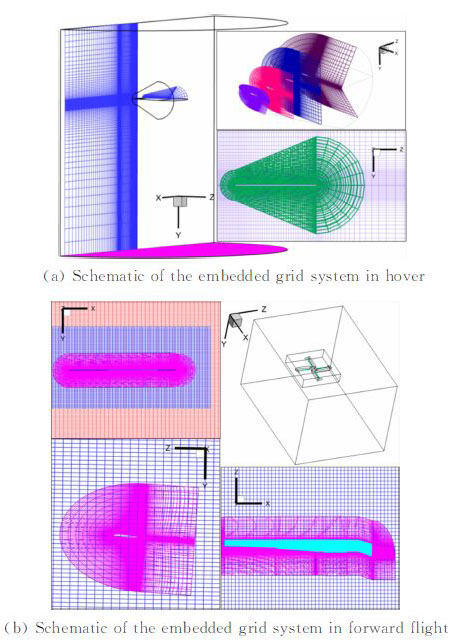
1.3 嵌套网格系统在旋翼嵌套网格系统的建立方面,嵌套网格系统由两部分组成:一是围绕桨叶的C-O型网格。为了保证网格的贴体性,在分布桨叶展向网格时充分虑了桨叶厚度和扭转角的变化,对剖面网格进行了合理的光顺。为了更好地模拟粘性效应,在桨叶前缘、后缘以及桨尖处对网格点进行了加密,其中桨叶法向第一层网格距桨叶表面的距离为1.0×10-5c(c为桨叶弦长),该网格随桨叶一起运动。二是旋翼网格嵌套所处的笛卡尔网格。为了能准确模拟出旋翼流场特性和桨尖涡的空间运动,悬停嵌套网格中旋翼周围的网格间距采用均匀尺寸0.1c,远场采用0.4c尺寸的间距;前飞嵌套网格中旋翼周围的网格间距采用均匀尺寸0.3c,远场采用0.4c尺寸的间距。背景网格由近场向远场线性过渡形成,为兼顾计算效率和精确捕捉前飞状态下的旋翼尾迹,在旋翼周围引入了一套网格间距为0.1c的过渡网格。根据上述原则,建立了分别用于悬停和前飞状态旋翼流场模拟的嵌套网格系统,如图 5所示,为了能清晰地显示网格之间的嵌套关系,这里对网格进行了粗化处理。
|
| 图 5 不同飞行状态下嵌套网格系统示意图 Fig. 5 Schematic of embedded grid system in different flight conditions |
为了进一步验证“预定边界”法的嵌套效率和稳定性,开展悬停状态旋翼不同总距下的网格嵌套试验,将本文方法与结合Inverse-Map方法的“透视图”方法进行了比较。
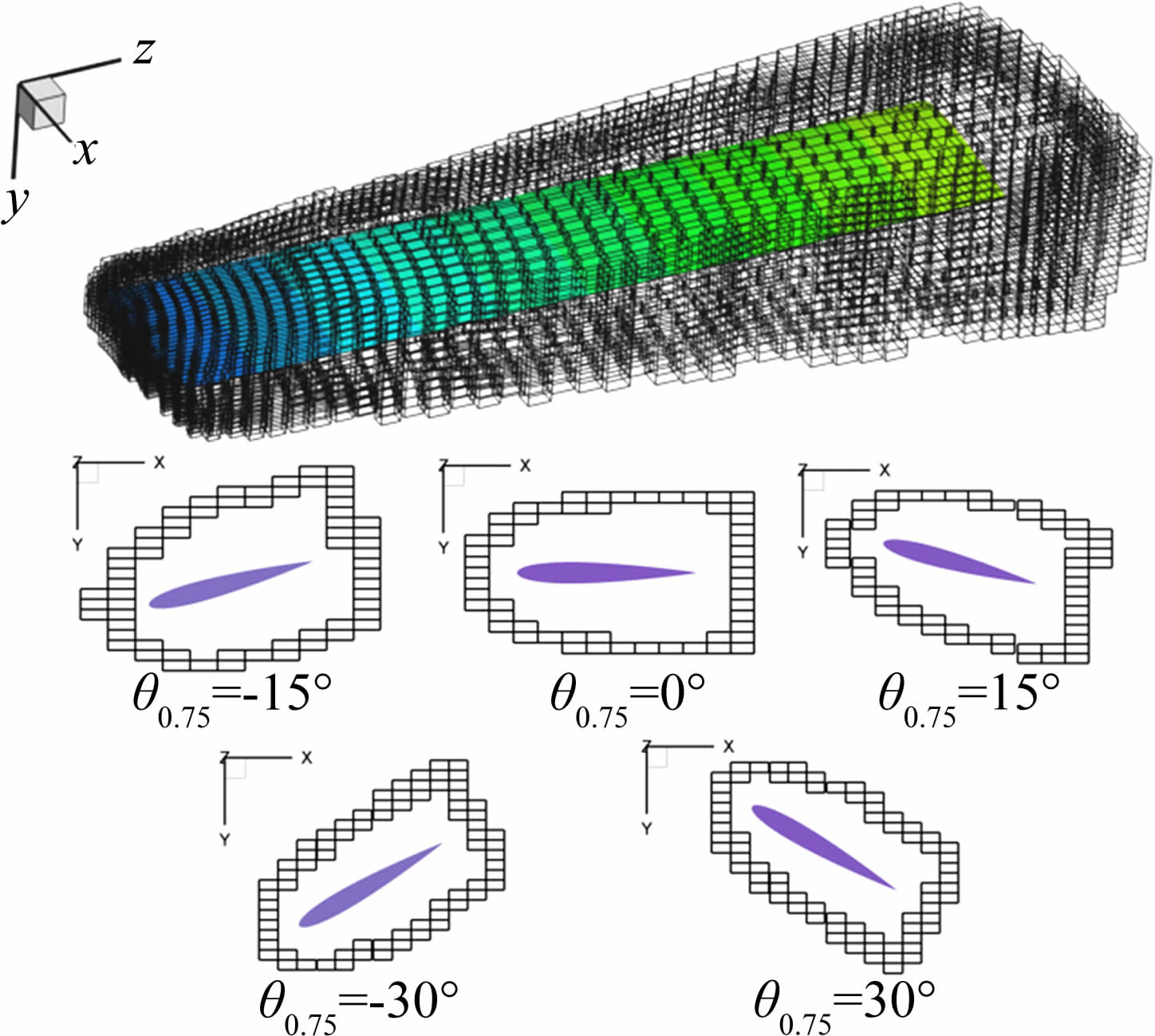
围绕C-T模型桨叶网格尺寸为265×49×76,背景网格尺寸为126×61×126,总距从-30°到30°,以每5°挖洞一次为研究算例。图 6给出了不同总距下的嵌套挖洞结果,从图 6中可以看出 “预定边界”嵌套方法能较好地封闭桨叶网格,且在不同总距时均能保证洞边界单元与翼面有合理的距离,从而有效地避开非线性区的影响,在一定程度上提高了插值精度。
|
| 图 6 不同总距下洞边界嵌套结果 Fig. 6 Results of hole boundary cells in different collective pitches |
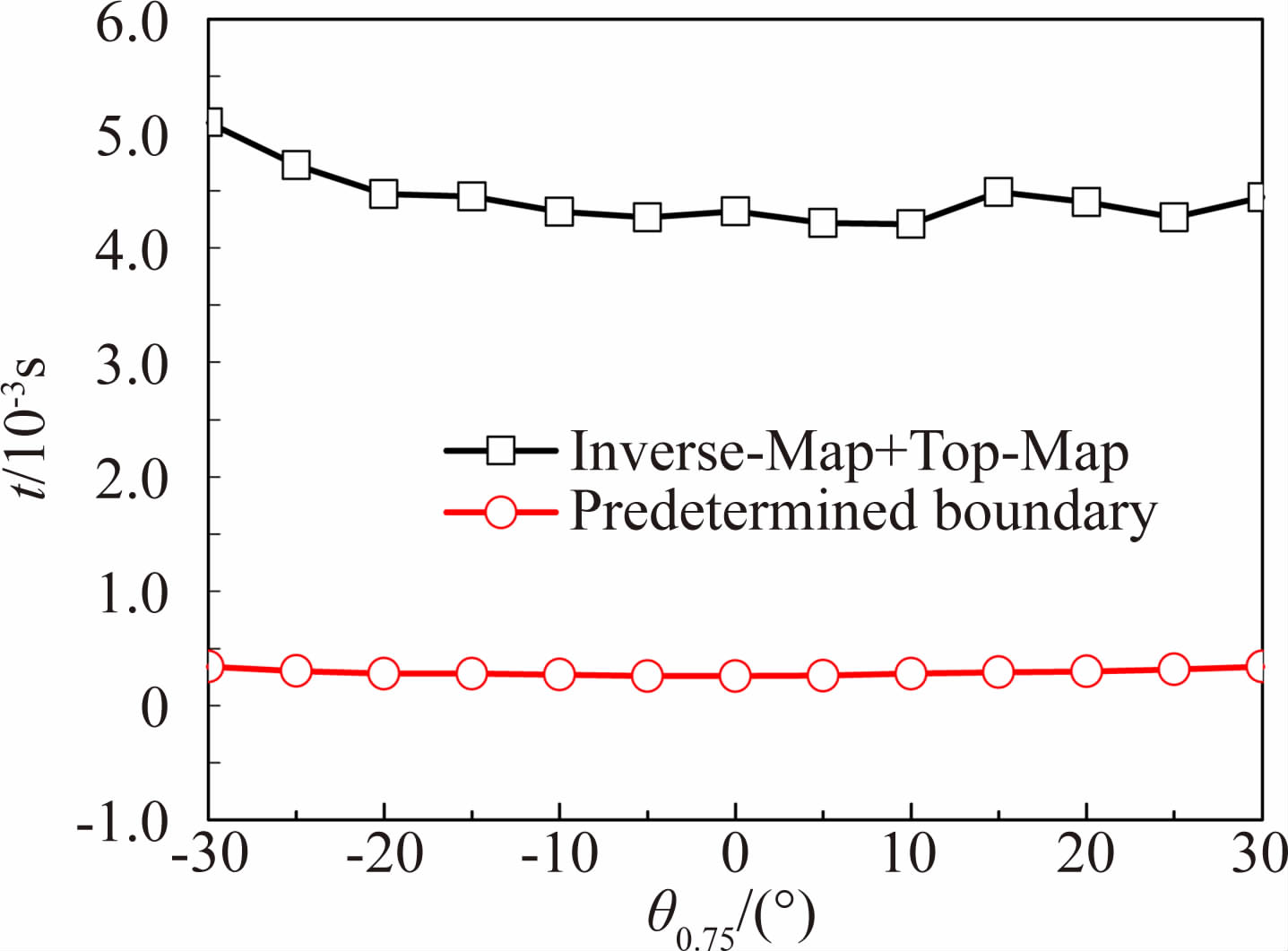
图 7给出了 “预定边界”法与结合Inverse-Map的最小“透视图”方法的嵌套时间对比。从图 7中可以明显地看出“预定边界”法相对于最小“透视图”方法,贡献单元嵌套所需的时间显著缩短,大约为其6%,验证了本文建立方法的高效性。此外,从图 7中还可以看出,当总距改变时,建立的方法相对于透视图方法的计算时间消耗波动较小,表明了该方法鲁棒性更高。这是由于“预定边界”法所形成的局部索引方法在该过程中很好地保证了贡献单元搜寻的有效范围,且具有较高的稳定性。
|
| 图 7 不同总距下挖洞和贡献单元搜索耗费总时间对比 Fig. 7 Comparisons of total consuming time of hole-cutting and donor cell searching at different collective pitches |
采用以绝对物理量为参数的守恒的积分形式的可压N-S方程作为主控方程:
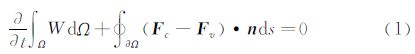

方程在时间离散上采用LU-SGS格式,在空间离散上采用格心形式的Jameson中心差分格式。为了避免激波和驻点附近出现非物理振荡及中心差分格式引起的奇偶失联,引入二、四阶混合导数组成的人工粘性项。用并行计算技术来加快收敛速度[13]。
2.3 边界条件对于粘性流体,桨叶表面采用物面无滑移边界条件,相应的热力学和动力学边界条件分别取作法向导数为0。S-A湍流模型边界条件为:远场边界入流取初始值,出流则采用内场外向插值。壁面气体温度根据绝热壁条件给定。
对于嵌套网格中的旋翼网格、过渡网格、背景网格之间的流场信息交换则由贡献单元与相应网格之间进行三线性插值来完成。
3 算例及结果分析为检验建立的嵌套方法的有效性,分别对不同旋翼的悬停和前飞状态流场进行了数值模拟。
3.1 悬停算例悬停算例验证中,采用的桨叶网格尺寸为265×49×76,背景网格为126×61×126,总网格量接近200万。为了加速数值模拟,在集群上(14个计算节点,单节点主频为3.2G)进行数值模拟。
(1) 首先选取具有代表性的含有两片矩形桨叶的C-T模型旋翼,桨叶展弦比为6,剖面翼型为NACA0012翼型,无负扭转。网格尺寸如上文所述,计算状态:Mtip=0.526,θ0.75=8°,Re=2.31×106。
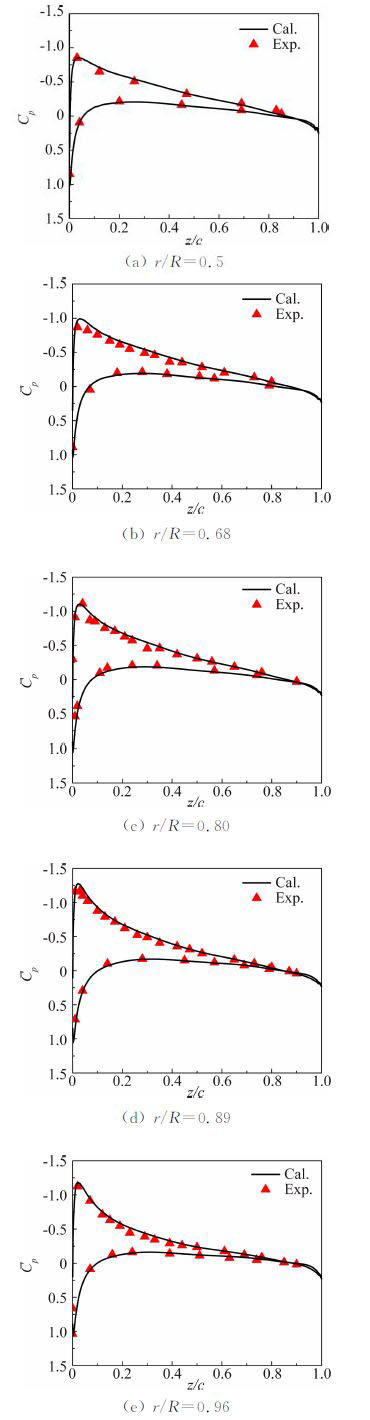
图 8分别给出了该状态下计算得到的桨叶不同剖面压强系数的分布结果与试验值[14]的对比。计算结果与试验值吻合较好,表明该嵌套网格方法能够用于悬停状态下的旋翼流场计算。
|
| 图 8 C-T旋翼悬停状态下的桨叶剖面压强分布对比 Fig. 8 Comparisons of pressure coefficient distributions on the C-T rotor blade in hover |
图 9分别给出了该状态下计算得到的涡量等值面和桨叶表面流线图。从图 9中可以看出,建立的嵌套方法在桨叶网格上能很好地捕捉旋翼桨尖涡的形态,并与背景网格中模拟获得的桨尖涡形成很好的对接关系,表明该嵌套网格方法能够很好进行旋翼近、远场的信息传递和流场计算。
|
| 图 9 悬停状态 C-T旋翼涡量等值面图和桨叶表面流线图 Fig. 9 Iso-surface of vorticity contours and surface streamlines of C-T rotor in hover |
(2) 进一步对复杂外形桨尖旋翼的嵌套网格方法的适应性进行研究。选取具有先进外形的UH-60A旋翼。该旋翼由四片桨叶构成,桨叶展弦比为15.3,具有非线性负扭转,最大负扭转角达到了13°,在93%处具有20°的常后掠。桨叶由两种翼型构成,桨叶根部和尖部采用SC1095翼型,桨叶中部采用SC1095-R8翼型。网格尺寸:桨叶网格265×49×76,背景网格121×198×134。计算状态: Mtip=0.628,θ0.75=9°,Re=2.75×106。
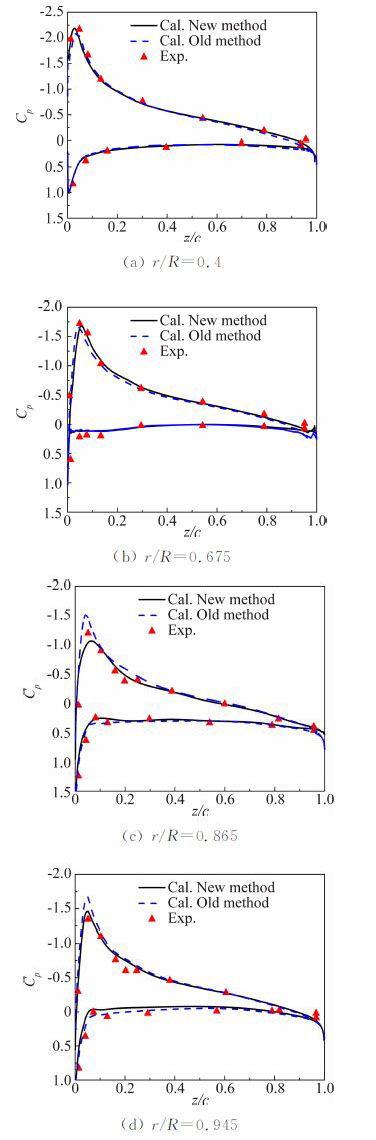
图 10给出了悬停状态下采用不同嵌套方法得出的剖面压强系数分布与试验值[15]的对比。从图 10 中可以看出,建立的方法对复杂外形的旋翼仍能进行较好地模拟,且计算值与试验值吻合较好。与采用文献[11]中的方法得出的计算结果相比,精度有了明显的提高,验证了该插值方法通过插值区域避开非线性区从而明显提高了流场模拟精度。
|
| 图 10 UH-60A旋翼悬停状态下的桨叶剖面压强分布对比 Fig. 10 Comparisons of pressure coefficient distributions on the UH-60A rotor blade in hover |
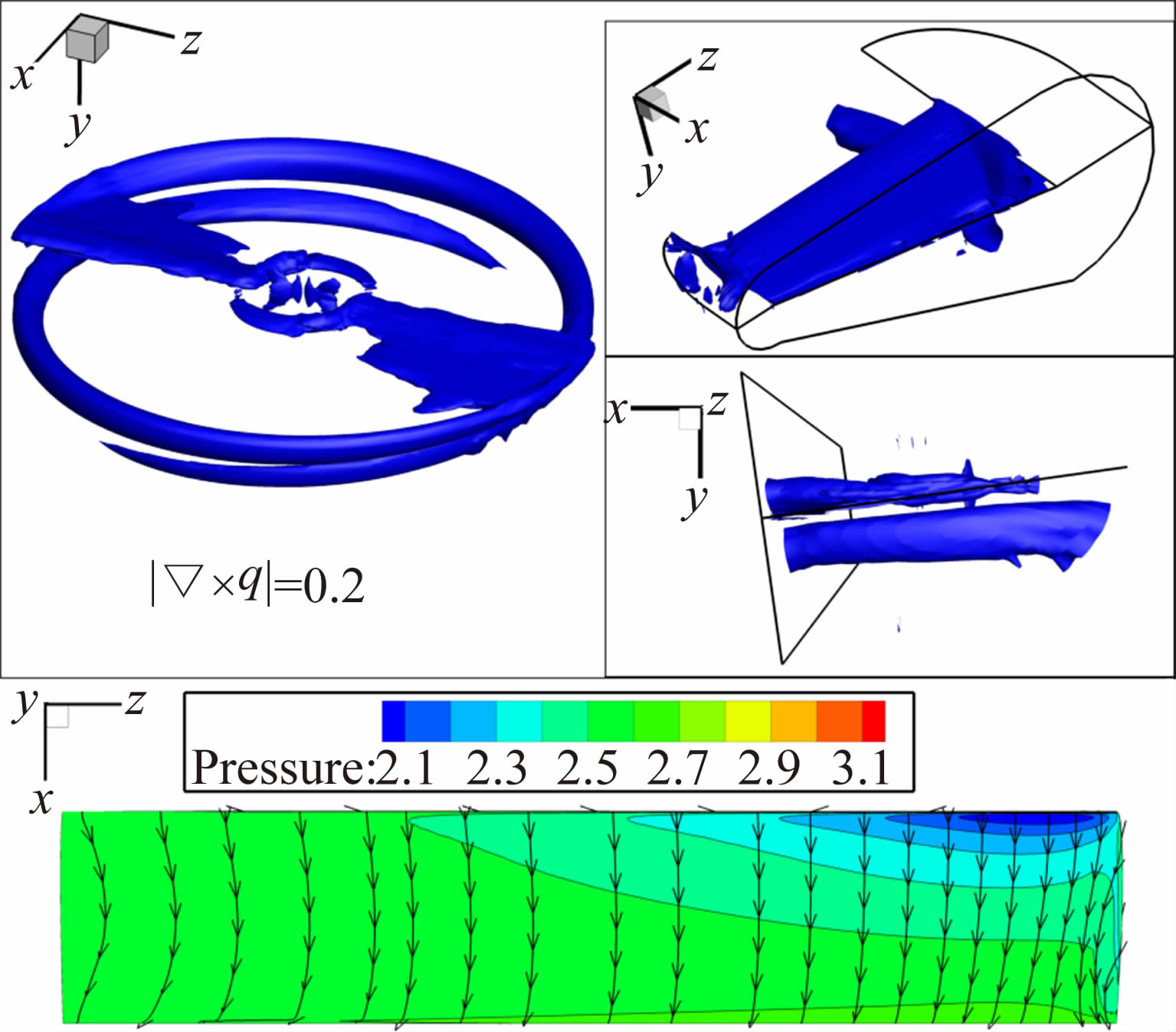
图 11为该状态下计算得到的旋翼流场涡量等值面图和桨叶表面压强分布图。从图 11中可以看出,前一片桨叶拖出的桨尖涡与后续桨叶下侧发生碰撞,形成桨-涡干扰现象,该干扰位置基本处于UH-60A桨尖后掠部分,这引起该桨叶剖面的压力波动。

|
| 图 11 悬停状态 UH-60A旋翼涡量等值面和桨叶表面压强分布 Fig. 11 Iso-surface of vorticity contours and surface pressure distributions of UH-60A rotor in hover |
前飞验证算例中采用的桨叶网格尺寸为265×49×76,过渡网格为126×61×126,背景网格为227×202×177,总网格量接近1300万。
(1) 首先选取C-T展弦比为7的前飞模型旋翼,含有两片矩形桨叶。计算状态:μ=0.2,Mtip=0.8,θ0.75=0°,Re=3.55×106。
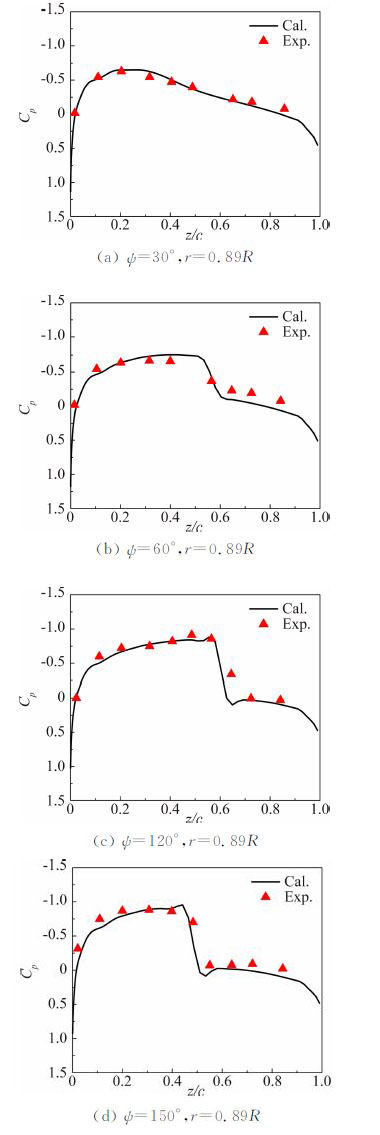
图 12给出了前飞状态下旋翼桨叶不同剖面压强系数计算值与试验值[14]的对比。从图 12中可以看出计算值与试验值吻合良好,且能较好地捕捉激波位置,表明所建立的嵌套网格方法能够用于前飞状态旋翼非定常流场的数值模拟研究。
|
| 图 12 前飞状态下C-T旋翼桨叶不同方位角压强系数分布 Fig. 12 Pressure coefficient distributions on C-T rotor blade at different azimuthal angle in forward flight |
(2) 选取大速度、中等过载飞行下的UH-60A旋翼进行数值模拟。计算状态:桨盘前倾角αtpp=-7.31°,μ=0.368,Mtip=0.642,总距操纵规律:θ0.75=12.55°+3.39°cosψ-8.62°sinψ。
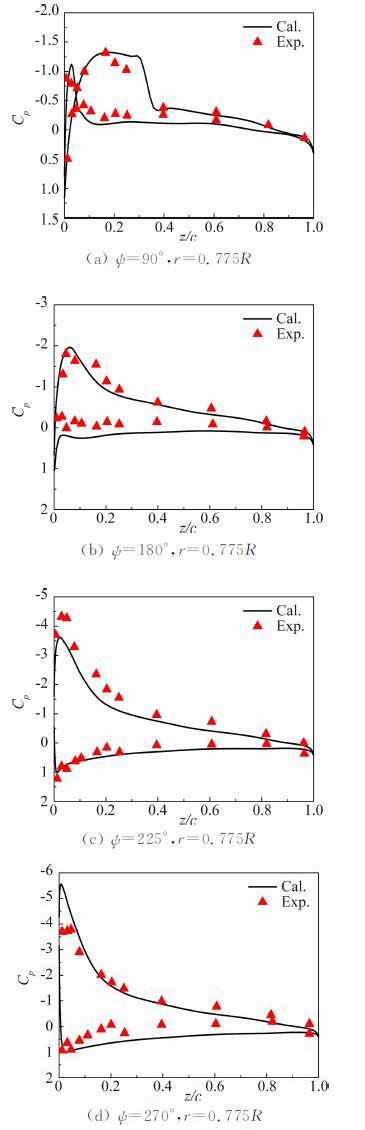
图 13给出了前飞状态下不同方位角处桨叶剖面的压强系数与试验值[15]的对比。在该飞行状态下, 各个方位角压强系数均能很好地贴合试验值,但在幅值上略有一定的差距,这是由于该状态下桨叶尖部可能出现较大的结构变形,而本文采用的是刚性旋翼假设,未考虑弹性造成的差异。但总体来说,本文的计算结果仍能很好地用于实际的旋翼设计分析,进一步表明所建立的“预定边界”嵌套网格方法对复杂外形的旋翼非定常状态模拟具有良好的适应性。
|
| 图 13 前飞状态下UH-60A桨叶不同方位角压强系数 Fig. 13 Pressure coefficient distributions on UH-60A blade at different azimuthal angle in forward flight |
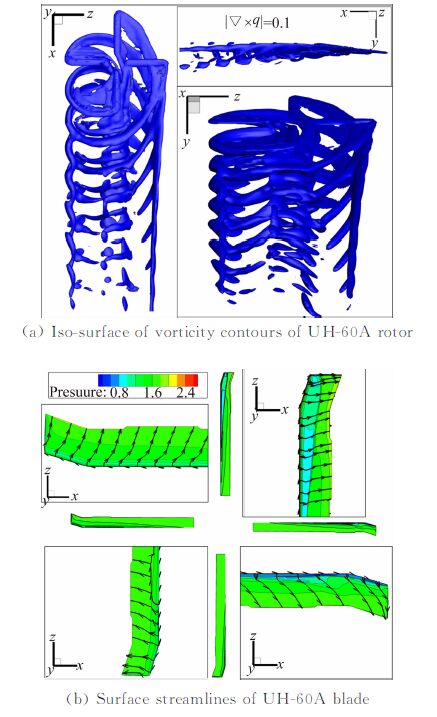
图 14分别给出了该状态下计算得到的涡量等值面图和桨叶表面流线图。从图 14中可以明显看出,建立的嵌套方法对复杂流场有较好的模拟作用,且对涡的捕捉精度较高。并且流线图很好地反映了前飞情况旋翼当地非对称来流的影响,特别是展向流动特征,表明所建立的网格方法和CFD方法能够很好地捕捉前飞非定常流场细节特性。
|
| 图 14 前飞状态C-T旋翼涡量等值面图和桨叶表面流线图 Fig. 14 Iso-surface of vorticity contours and surface streamlines of UH-60A rotor in forward |
本文提出并建立了适用旋翼流场计算的“预定边界”嵌套网格方法。根据各项算例的计算结果,得出以下结论:
(1) 提出的“逆向边界”能很好地避开旋翼流场的非线性区域,且在不同操纵条件下均能很好地保证洞边界的封闭性和到翼面距离的一致性,并在一定程度上提高了流场模拟的精度。
(2) 提出的结合 “逆向边界”方法和LDP方法形成的“预定边界”嵌套方法能够较为方便地用于贡献单元的搜寻,并很好地简化了嵌套流程,相对于结合“Inverse-Map”的“透视图”方法,在鲁棒性和嵌套效率方面均有了明显提高。
(3) 结合发展的嵌套网格方法,建立了旋翼非定常流场的CFD方法,验证了该方法能满足旋翼数值模拟所需的精度,为进一步开展高性能旋翼气动设计分析打下了良好的基础。
| [1] | Woodgate M A, Barakos G N. Implicit CFD methods for fast analysis of rotor flows[R]. AIAA 2012-0421. |
| [2] | Yashwanth Ganti, James D Baeder. CFD analysis of a slatted UH-60 rotor in hover[R]. AIAA 2012-2888. |
| [3] | Thomas D Economon, Francisco Palacios, Juan J Alonso. Optimal shape design for open rotor blades[R]. AIAA 2012-3018. |
| [4] | Tung W, Lin J X, Hsiang-Chun Kuan. Aerodynamic analysis of helicopter rotor blades in heavy rain condition[R]. AIAA 2013-0653. |
| [5] | La Bozzetta W F, Gatzke T D. MACGS-towards the complete grid generation system[R]. AIAA 94-1923-CP. |
| [6] | Slotnick J P, Kandula M, Buning P G. Navier-Stokes simulation of the space shuttle launch vehicle flight transonic flowfield using a large scale chimera grid system[C]//12th AIAA Applied Aerodynamic Conference. Colorado Spings, Colorado, USA, 1994. |
| [7] | Meakin R L. A new method for establishing intergrid communication among systems of overset grids[R]. AIAA 1991-1586. |
| [8] | Li T H, Yan C. A new method of hole-point search in grid embedding technique[J]. Acta Aerodynamica Sinica, 2001, 19(2):156-160. (in Chinese)李亭鹤,阎超.一种新的分区重叠洞点搜索方法-感染免疫法[J].空气动力学学报, 2001, 19(2):156-160. |
| [9] | Ye L, Zhao Q J, Xu G H. Numerical simulation of flowfield of helicopter rotor and fuselage in forward flight based on unstructured embedded grid technique[J]. Journal of Aerospace Power, 2009, 24(4):904-909. (in Chinese)叶靓,招启军,徐国华.非结构嵌套网格的直升机旋翼/机身前飞流场数值模拟[J].航空动力学报, 2009, 24(4):904-909. |
| [10] | Yang W Q, Song B F, Song W P. Distance decreasing method for confirming corresponding cells of overset grids and its application[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(2):205-212. (in Chinese)杨文青,宋笔锋,宋文萍.高效确定重叠网格对应关系的距离减缩法及其应用[J].航空学报, 2009, 30(2):205-212. |
| [11] | Wang B, Zhao Q J, Xu G, et al. A new moving-embedded grid method for numerical simulation of unsteady flow-field of the helicopter rotor in forward flight[J]. Acta Aerodynamica Sinica, 2012, 30(1):14-21. (in Chinese)王博,招启军,徐广,等.一种适合于旋翼前飞非定常流场计算的新型运动嵌套网格方法[J].空气动力学学报, 2012, 30(1):14-21. |
| [12] | Spalart P R, Allmaras S R. A one equation turbulence model for aerodynamic flows[C]//30th Aerospace Sciences Meeting & Exhibit, 1992. |
| [13] | Du Z H. Parallel programming techniques of high performance computing MPI parallel programming design[M]. Beijing:Tsinghua University Press, 2001. (in Chinese)都志辉.高性能计算并行编程技术-MPI并行编程设计[M].北京:清华大学出版社, 2001. |
| [14] | Caradonna F X, Tung C. Experimental and analytical studies of a model helicopter rotor in hover[J]. Vertica, 1981, 5(1):149-161. |
| [15] | Sitaraman J, Baeder J D, Chopra I. Validation of UH-60A rotor blade aerodynamic characteristics using CFD[C]//Proceedings of the 59th Annual Forum of the AHS, 2003. |



