2. 美国加州大学尔湾分校机械与宇航工程系, 美国加利福尼亚 62697
2. University of California, Irvine, California 92697-3975, USA
0 引 言
现代高机动战斗机、导弹等飞行器通常具有类似尖头旋成体的细长前体,当迎角增大到一定程度,其分离涡流场会从对称变得非对称,同时伴随有方向和大小均无法预估的侧向力/力矩,这对飞行器的操纵性和稳定性有很大影响[1, 2, 3, 4]。因而在大迎角下实现对细长体上侧向力/力矩的控制,对飞行器气动设计具有重要的意义。同时这个分离涡流场对细长体头部尖端处的扰动非常敏感,从而给通过注入很少的能量来主动控制飞行器的侧向力提供了可能性。
Hanff等[5]在细长尖拱前体头部安装了两个向前吹气的气管,并通过改变占空比来控制左右舷气孔交替吹气,以此来控制平均的横向气动力/力矩。这种方法利用了前体涡内在的双稳态特性,有意使涡对在两个稳定状态之间按一定的频率转换。明晓和顾蕴松[6, 7]等在细长旋成体头部靠近尖端处设置可以自动控制的微小的扰动片,利用该扰动片的往复振荡实现了对细长体大迎角下侧向力的比例控制。王延奎等[8]在某型飞机模型头部使用微三角块和背风侧单孔微吹气组合作用,对大迎角下的非对称侧力实现有效控制。
近年来,等离子体流动控制技术受到国内外很多研究团队的关注[9, 10],研究者将等离子体流动控制方式也应用到了细长前体非对称分离流动的控制中。Liu Feng等[11]、孟宣市等[12]的研究表明,在大迎角下,通过分布在细长圆锥前体尖端处一对SDBD(Single Dielectric Barrier Discharge)激励器,配合占空循环技术,可以实现圆锥前体侧向力和力矩的比例控制。
本文在上述工作基础上,在压力测量的同时进行了当地截面速度场的PIV测量,并通过表面压力和空间二维速度场的分析,研究了等离子体激励对圆锥前体分离涡位置及其特性的影响。
1 模型及实验设备实验在西北工业大学NF-3低速直流闭口风洞中进行,实验段截面尺寸为3.0 m×1.6 m。实验迎角为45°,实验风速为5 m/s。基于圆锥段底面直径的雷诺数为5×104。
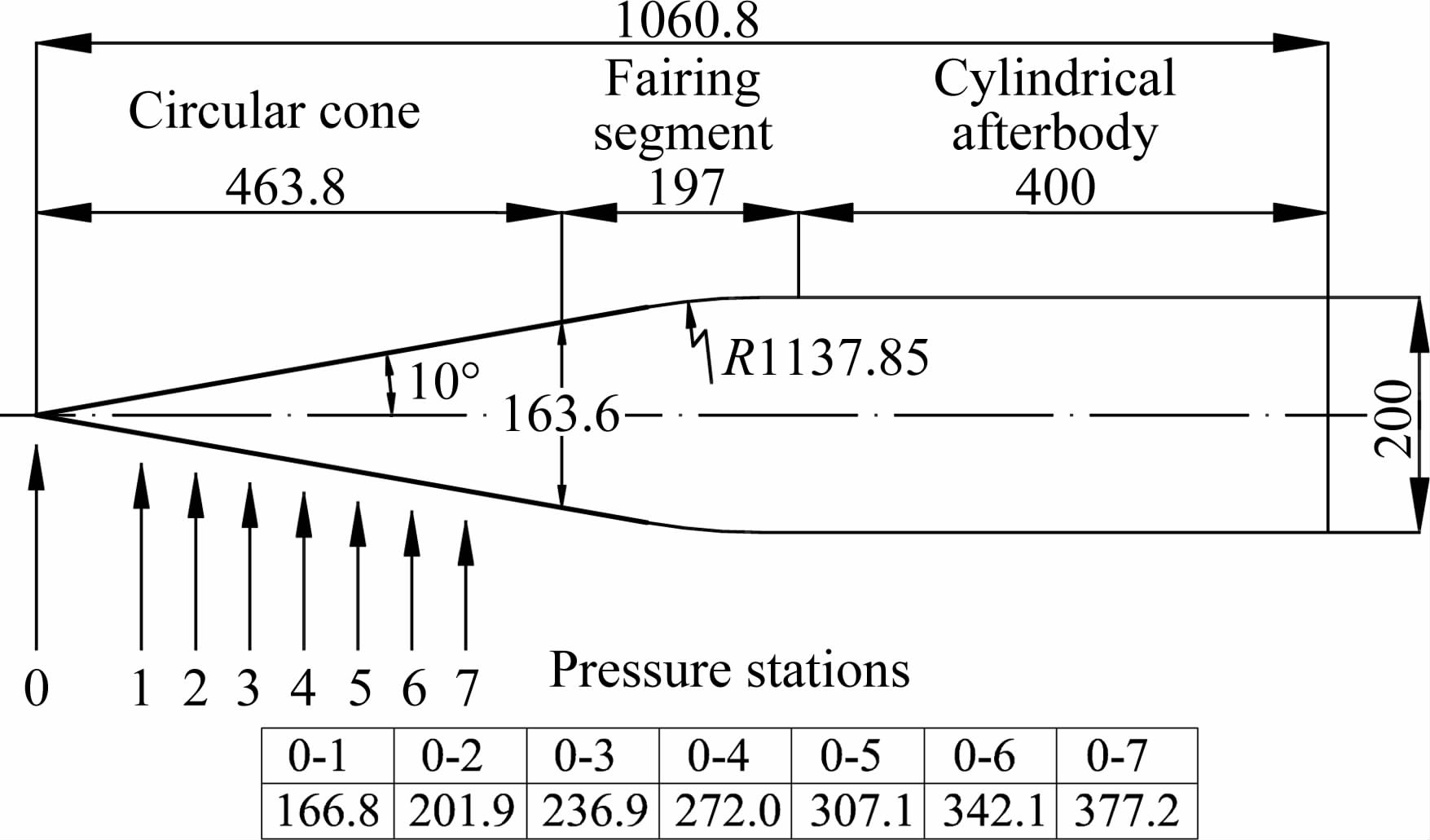
模型圆锥段共设置7个测压截面,从尖端36%到81%处等距分布(如图 1)。每个测压截面上间隔10°方位角均匀分布36个测压孔。压力测量采用PSI公司生产的9816型压力扫描阀,采集频率为100Hz。文中使用的压力数据均为第2截面上15s内采集的压力值的算术平均值。当地截面侧力系数CYd是由压力分布积分得到的侧向力由当地截面直径d无量纲化得到,指向右舷时为正。
|
| 图 1 实验模型(单位: mm) Fig. 1 Test model(unit: mm) |
圆锥头部长度为150 mm的部分为绝缘材料,其余部分为金属。圆锥全长463.8 mm,底面直径为163.6 mm。如图 2(a)所示,在圆锥头部靠近尖端处安放了一对对称的长条形单电极介质阻挡放电(SDBD)等离子体激励器。激励器由不对称的两条厚度为0.03 mm铜电极组成。使用聚酰亚胺绝缘层将下电极完全覆盖住并包裹在圆锥头部。两个激励器中心线方位角θ分别为±120°(图 2(a))。方位角定义为面向来流方向,顺时针为正,0°方位角在模型迎风面正中。电极前缘距模型尖端为9 mm,沿圆锥母线的长度为20 mm。上、下电极宽度分别为1 mm和2 mm。上、下电极间隔1.5 mm(图 2(b)),等离子体就在这个间隙附近产生,并以诱导射流的形式为流动注入动量[9]。在静止大气条件下该等离子体激励器诱导出的气流方向由上电极指向下电极,诱导气流的大小根据等离子体激励器激励电压、频率等因素改变,最大诱导风速约4 m/s。

|
| 图 2 等离子体激励器 Fig. 2 Plasma actuators |
实验中使用了三种等离子体激励器工作模式:(1)激励器关(两侧激励器都不工作);(2)左舷激励器开(左舷激励器工作,右舷激励器不工作);(3)右舷激励器开(右舷激励器工作,左舷激励器不工作)。圆锥模型上的每个激励器单独由交流电源供电。电源输出的是峰-峰电压值Vp-p约为14 kV的正弦波(Alternative Current,AC),频率约为8.9kHz。单侧等离子体激励器工作时电源输入功率约为19.3 W。
使用丹迪(Dantec Dynamic)公司生产的二维粒子图像测速系统(Particle Image Velocimetry,PIV),Nd∶YAG激光器,功率≤200 mJ,相机像素为1600×1200。相机固定在测量平面的下风向处的迎角控制台上。对位于第二截面处的空间流场进行了观测,图 3为PIV实验布局。PIV采集时每对脉冲间距为60 μs,数据处理时收索区域为32像素×32像素,重叠区设置为50%,脉冲重复频率为9 Hz,数据处理每个状态持续采集10 s,并对10 s内采集的结果进行平均。PIV示踪粒子是从风洞入口处点燃烟饼产生的,并由风洞入口吸入风洞内,粒子直径约1 μm。

|
| 图 3 PIV实验布局 Fig. 3 PIV test layout |
图 4给出了激励器三种工作模式下的PIV结果。当流动逆时针时轴向涡量ωx为正,顺时针时为负。PIV结果中给出的z/d和y/d表示x、y方向坐标用当地直径无量纲化的结果。

|
| 图 4 速度向量和轴向涡量云图 Fig. 4 Velocity vectors and axial-vorticity contours |
左舷等离子体激励器诱导气流的作用点在θ=120°处,诱导出逆着来流方向的气流。从图 4(a)中可以看出这个由等离子体诱导出的左侧逆着来流方向的气流与旋涡产生相互作用,使得左舷一侧的剪切层及其卷起的涡移动到了远离模型的位置,右舷一侧的剪切层及其卷起的涡移动到更靠近物面的位置。
右舷激励器开时旋涡的流动状态(如图 4b)基本上与左舷激励器开时反向对称。右舷激励器诱导气流的的作用点位于θ=-120°处。此时左舷一侧的剪切层及其卷起的涡移动到靠近物面处,右舷一侧的剪切层及其卷起的涡则移动到远离模型的位置。
左、右舷激励器分别开启状态下,压力分布及PIV显示测量截面上的流场并没能达到精确的双稳态。这些误差可能是由于模型以及等离子体激励器安装的几何误差造成的,也可能是由于涡本身的跳动等原因[13]造成的。但是,PIV实验结果清楚地证实了等离子体激励器在控制双稳态涡结构中所起的作用。
等离子体激励器关状态下(如图 4c),左舷一侧的剪切层沿着模型截面圆周弯曲然后卷起一个位置靠近模型表面的涡。同时右舷方向的剪切层远离模型表面,其卷起的涡也处在远离模型表面的位置,此时的流动状态和右舷激励器开的状态很相似。在实验中发现同一个模型在同样是等离子体激励器关的状态下产生的压力分布以及分离涡的位置在重复实验中会随机的出现双稳态中的一种状态[1]。事实上,细长旋成体在大迎角无控制状态下的非对称侧向力是由自由来流或模型头部尖端处的微小不对称扰动决定的[1]。但是,在三次实验中左舷激励器开和右舷激励器开时的非对称的流动状态总是保持不变的。
PIV结果上可以看到测量截面上有一个切向速度很低的点,将该点定义为涡心,坐标为(yC,zC)。本文中涡心是通过分析过该点的水平和垂直速度分布来确定的。
表 1给出了在三种激励器工作模式下的涡心坐标、附面层分离点和局部侧力系数(CYd)。左舷激励器开状态下左舷一侧的涡心明显高于右舷一侧。右舷激励器开和激励器关状态下左舷一侧的涡心位置比起右舷一侧的涡更接近于模型对称面。虽然右舷激励器开和激励器关时流动状态很相似,但是右舷激励器开时产生的局部侧向力比激励器关时产生的要大16%(表 1)。
| Mode | CYd | Port side | Stardboard side | ||||
| Vortex core center | Separation location | Vortex core center | Separation location | ||||
| yc/d | zc/d | yc/d | zc/d | ||||
| Port-on | 0.88 | -0.25 | 0.72 | 90° | 0.24 | 0.33 | -110° |
| Starboard-on | -1.22 | -0.03 | 0.43 | 100° | 0.47 | 0.45 | -100° |
| Plasma-off | -1.05 | -0.07 | 0.41 | 100° | 0.57 | 0.43 | -100° |
同样可以从压力分布看出流动非对称的情况,图 5比较了三种工作模式下的压力分布。左、右舷激励器开状态下的压力分布接近反向对称,但并不是完全精确的镜像对称,其原因和前文中提到的一样是由模型以及激励器的几何不对称还有旋涡本身的抖动造成的。表 1比较了三种状态下流动分离点的方位角,分离点的方位角是由压力分布推测得到的[14],当地侧向力系数也是由压力分布计算得到的。左舷激励器开时左舷一侧附面层分离点方位角和激励器关状态相比向迎风面移动了10°,同时右舷一侧附面层分离点的方位角向着背风面移动了10°。和激励器关状态相比左舷激励器开时左舷侧的吸力峰值较低右舷侧的吸力峰值较高,同时等离子体激励器关和左舷等离子体激励器开时的局部侧力方向相反。

|
| 图 5 对比三种激励器工作模式下的压力分布 Fig. 5 Comparison of pressure distributions forthree models of plasma actuation |
次涡核的特性可以通过围绕涡心的切向速度分布来研究[15, 16](次涡核并不是多次涡,而是通过旋涡切向速度定义的涡核部分)。过涡心并平行于y轴和z轴的切向速度分别是由w和v来表示的。研究中分别画出了三种等离子体激励器工作模式下切向速度分布,图 6只给出了左舷激励器开模式下左舷侧涡的结果。

|
| 图 6 左舷侧涡心沿y轴和z轴的切向速度分布, 左舷激励器开 Fig. 6 Tangential velocity along horizontal and vertical lines passing through port side vortex core center,port-on |
涡心处的切向速度为0,距离涡心较远处的速度逐渐接近v=0和w=0.7U∞。切向速度从涡心处开始近似线性地升高到最大值,然后开始下降,但是下降的速度较慢。将切向速度达到最大值的点定义为次涡核的边界,这点到涡心的距离则为次涡核半径r。从图 6中可以看出,在次涡核内部切向速度分布沿涡半径方向近似线性增加,就像理论上的兰金涡模型(Rankine vortex)一样接近一个旋转的固体。
过涡心平行于y轴和z轴的两个切向速度的最大值出现的位置距离涡心的位置并不相同,这说明涡心并不是在涡核的几何中心上。表 2给出了沿x、y方向次涡核几何中心与涡心的偏差,分别用Δy和Δz表示。左舷等离子体激励器开时左舷一侧的涡心向着右上方偏移,同时右舷一侧的涡心则向着左下方偏移。右舷等离子体激励器开时左舷一侧的涡心向上偏移,同时右舷一侧的涡心向着左上方移动。当等离子体激励器关时涡心基本上没有偏移。这就是说等离子体激励器的作用加剧了涡心从次涡核几何中心处偏移的程度。
| Mode | Port-side vortex | Starboard-side vortex | ||
| Δy/d | Δz/d | Δy/d | Δz/d | |
| Port-on | 0.1 | 0.1 | -0.1 | -0.1 |
| Starboard-on | 0.0 | 0.1 | -0.1 | 0.1 |
| Plasma-off | 0.0 | 0.0 | 0.0 | 0.1 |
最大轴向涡量ωx和其所在的位置是由PIV图像通过和找涡心同样的方法得到。表 3给出了最大轴向涡量及其位置,就像前面从PIV图像中看到等离子体激励器关时的右舷一侧涡核消失的结果一样,右舷一侧涡的最大涡量值明显低于左舷一侧涡的涡量。无论左舷还是右舷等离子体激励器的作用下右舷一侧涡的轴向涡量都变大到了和左舷一侧涡到同一个量级上。在三种状态下左舷一侧涡的最大轴向涡量值出现的位置基本上和涡心的位置重合(见表 1)。但等离子体激励器关状态下右舷一侧涡的差别较大。这可能是右舷一侧涡的消失引起的。
| Mode | Port-side vortex | Starboard-side vortex | ||||
| ωxd/U∞ | y/d | z/d | ωxd/U∞ | y/d | z/d | |
| Port-on | -14.1 | -0.30 | 0.66 | 13.6 | 0.16 | 0.33 |
| Starboard-on | -15.8 | -0.05 | 0.50 | 13.8 | 0.57 | 0.33 |
| Plasma-off | -18.7 | -0.11 | 0.43 | 11.6 | 0.59 | 0.27 |
研究中分别画出了三种等离子体激励器工作模式下过涡量极值点的水平线和垂直线的涡量分布图。图 7只给出了左舷激励器开模式下左舷侧涡的结果。轴向涡量分布的曲线比切向速度变化的曲线波动的要剧烈得多。轴向涡量随着离涡量极值点的距离增大而减少。将轴向涡量接近于0的那一点定义为涡核边界,这点到涡量极值点的距离则为涡核半径R。

|
| 图 7 左舷激励器开时左舷侧沿过涡量极值点的水平和垂直方向的轴向涡量分布 Fig. 7 Distribution of axial vorticity along horizontal and vertical lines passing through maximum vorticity point for port-on,port side |
图 8给出了等离子体激励器三种工作状态下涡心附近的最大切向速度vΘ,max、次涡核平均半径r、涡核的平均半径R沿着以涡心为原点的极坐标角度Θ的变化。因为右舷一侧的涡有时候会消失,所以给出了左舷一侧涡的情况。

|
| 图 8 左舷涡最大切向速度、涡核半径、 次涡核半径沿着极坐标角度Θ的分布 Fig. 8 Distributions of maximum tangential velocity, sub-core radius and core radius of port-side vortex |
通过定量分析最大切向速度、涡核、次涡核半径及其比值的变化和沿次涡核边界的环量(表 4),可以看出沿着次涡核一周的速度环量Γ是通过次涡核半径分布和最大切向速度沿着Θ分布计算得到的。在等离子体激励器的作用下,涡核的平均半径R明显增大了70%,平均的次涡核半径r只增大了10%~40%,这也就是说在激励器关状态下次涡核半径相对与涡核半径变得更小了。切向速度最大值的平均值vΘ,max降低了。沿左舷侧次涡核边界一周的环量Γ在左舷激励器作用下增大了约20%。Γ在右舷激励器工作时略有减小。对照表 1中的旋涡位置和侧向力系数的变化可以看出,在激励器的作用下使得分离涡的涡核、次涡核特性产生了变化,该变化与分离涡的相对位置以及分离点产生了相互作用。但影响细长体侧向力的主要因素是分离涡的相对位置。
| Mode | vΘ,max/U∞ | r/d | R/d | r/R | Γ/dU∞ |
| Port-on | 0.54 | 0.21 | 0.35 | 0.60 | 0.80 |
| Starboard-on | 0.58 | 0.17 | 0.33 | 0.52 | 0.62 |
| Plasma-off | 0.72 | 0.15 | 0.20 | 0.75 | 0.66 |
在半顶角为10°的圆锥前体模型头部尖端处的特定位置安装了一对等离子体激励器,实现了圆锥前体在低风速大迎角下侧向力的控制。使用二维粒子图像测速技术和压力测量技术证实了等离子体激励器对圆锥前体在大迎角下分离涡的控制作用。
(1) 在等离子体激励的作用下,与其同侧的附面层分离点推向迎风面,同时将另一侧的分离点拉向背风面方向。吸力峰值在激励器工作的这一侧减弱,同时在另一侧加强。同侧的分离剪切层及其卷起的涡向外移动同时另一侧的向着靠近模型的方向移动。
(2) 在重复实验中,左/右舷激励器开状态下流动的非对称状态始终保持一致,但激励器关状态下的流动非对称状态则有可能改变。验证了等离子体激励器对大迎角下前体分离涡流场的控制作用。
(3) 任意一侧等离子体激励器的作用都会使双侧涡心位置从次涡核的几何中心处发生偏移。
(4) 任意一侧激励器工作时左舷侧涡核以及次涡核的尺寸都明显变大,且涡核半径变大更为明显。
| [1] | Ericsson L. Sources of high alpha vortex asymmetry at zero sideslip[J]. Journal of Aircraft, 1992, 29(6):1086-1090. |
| [2] | Zilliac G G, Degani D, Tobak M. Asymmetric vortices on a slender body of revolution[J]. AIAA Journal, 1991, 29(5):667-675. |
| [3] | Liu P Q, Deng X Y. Lee-side vortex structure and aerodynamic characteristics analysis over a slender cylinder at high incidence[J]. Acta Mechanics Sinica, 2002, 34(2):248-255. (in Chinese)刘沛清,邓学蓥.大迎角细长体绕流背涡结构与气动特性分析[J].力学学报, 2002, 34(2):248-255. |
| [4] | Bo N, Deng X Y, Ma B F, et al. The effect of critical Reynolds number and zonal characteristics on asymmetric vortices at forebody[J]. Acta Aerodynamica Sinica, 2009, 27(5):529-535. (in Chinese)柏楠,邓学蓥,马宝峰,等.前体非对称涡流动临界雷诺数效应及分区特性[J].空气动力学学报, 2009, 27(5):529-535. |
| [5] | Hanff E, Lee R, Kind R J. Investigations on a dynamic forebodey flow control system[C]. Proceedings of the 18th International Congress on Instrumentation in Aerospace Simulation Facilities. Inst. of Electrical and Electronics Ehgineers. Piscataway, NJ, 1999. |
| [6] | Ming X, Gu Y. An innovative control technique for slender bodies at high angle of attack[C]. 3rd AIAA Flow Contronl Conference. San Francisco, California, 2006. AIAA 2006-3688. |
| [7] | Gu Y S, Ming X. Proportional side force control of slender body at high angle of attack[J]. Acta Aeronoutica et Astronautica Sinica, 2006, 27(5):746-750. (in Chinese)顾蕴松,明晓.大迎角细长体侧向力的比例控制[J].航空学报, 2006, 27(5):746-750. |
| [8] | Wang Y K, Wei Z F, Deng X Y, et al. An experimental study on forebody vortex flow control technique using combined perturbation[J]. Chinese Journal of Theoretical and Applied Mechanics, 2007, 39(4):433-441. (in Chinese)王延奎,魏占峰,邓学蓥,等.飞机大迎角非对称涡组合扰动主动控制研究[J].力学学报, 2007, 39(4):433-441. |
| [9] | Zhang P F, Wang J J, Shi W Y, et al. Experimental study on the separation control by plasma actuator in subsonic flow[J]. Journal of Experiments in Fluid Mechanics, 2007, 21(2):35-39. (in Chinese)张攀峰,王晋军,施威毅,等.等离子体激励低速分离流动控制实验研究[J].实验流体力学, 2007, 21(2):35-39. |
| [10] | Li Y H, Liang H, Ma Q Y, et al. Experimental investigation on airfoil suction side flow separation by pulse plasma aerodynamic actuation[J]. Acta Aeronoutica et Astronautica Sinica, 2008, 29(6):1429-1435. (in Chinese)李应红,梁华,马清源,等.脉冲等离子体气动激励抑制翼型吸力面流动分离的实验[J].航空学报, 2008, 29(6):1429-1435. |
| [11] | Liu F, Luo S J, Gao C, et al. Flow control over a conical forebody using duty-cycled plasma actuators[J]. AIAA Journal, 2008, 46(11):2969-2973. |
| [12] | Meng X S, Guo Z X, Luo S J, et al. Control of asymetric vortices over a slender conical forebody using plasma actuators[J]. Acta Aeronoutica et Astronautica Sinica, 2010, 31(3):500-505. (in Chinese)孟宣市,郭志鑫,罗时钧,等.细长圆锥前体非对称涡流场的等离子体控制[J].航空学报, 2010, 31(3):500-505. |
| [13] | Orloff K L. Trailing vortex wind-tunnel diagnostics with a laser velocimeter[J]. Journal of Aircraft, 1974, 11(8):477-482. |
| [14] | Hall R M. Influence of Reynolds number on forebody side forces for 3.5-diameter tangent-ogive bodies[C]. NASA Langley Research Center. Hampton, Virginia, 1987. AIAA 87-49056. |
| [15] | Beresh S J, Henfling J F, Spillers R W. Planar velocimetry of a fin trailing vortex in subsonic compressible flow[C]. 38th Fluid Dynamics Conference and Exhibit. Seattle, Washington, 2008. AIAA 2008-4179. |
| [16] | Beresh S J, Henfling J F, Spillers R W. Planarvelocimetry of a fin trailing vortex in subsonic compressible crossflow[J]. AIAA Journal, 2009, 47(7):1730-1740. |


