2. 中国空气动力研究与发展中心计算空气动力研究所, 四川绵阳 621000
2. Computational Aerodynamics Institute of China Aerodynamics Research and Development Center, Mianyang 621000, China
0 引 言
随着计算机技术和CFD方法的飞速发展，CFD已经获得了广泛的应用，不仅引起了飞行器设计思想的变革，导致高性能飞行器的诞生，同时在复杂流动机理研究等方面也发挥了重要作用。然而目前广泛应用的CFD软件大多基于二阶精度格式。对于只涉及附着流和小分离流的问题，二阶精度格式能够给出较好的模拟结果，但是对于复杂流动问题，特别是涉及到导数计算的摩阻和热流计算，二阶精度格式难以满足科学研究和工程应用的精度要求。
高阶精度方法近年来获得了广泛、深入的研究，发展了一系列高阶精度格式，如ENO、WENO、DCS、WCNS和DG等。与二阶精度格式相比较，高阶精度格式具有高分辨率、低耗散等特点，能够给出更加精细的流动结构和更准确的计算结果，已经被广泛应用于流动机理、气动声学、大涡模拟(LES)和直接数值模拟(DNS)等科学研究领域。但是，针对复杂的工程问题，目前尚没有一种实用的高阶精度计算方法与数值模拟软件。主要原因在于高阶精度方法对计算网格的质量要求高，计算效率低，鲁棒性差等。
五阶空间离散精度的WCNS[1, 2, 3, 4, 5]格式作为一种非线性高阶精度空间离散格式，不仅具有高分辨率、低耗散、低色散和一致高阶精度等特点，而且对间断具有很好的捕捉能力。其显式格式WCNS-E，在保持上述优良特性的前提下，相比隐式紧致格式，进一步提高了计算效率。特别是，文献[6]针对高阶有限差分算法在满足几何守恒律方面的困难，发展了满足几何守恒律的高阶精度的网格坐标变换导数算法，大大提高了WCNS-E格式对复杂计算网格的适应性和鲁棒性，显示了WCNS-E格式在复杂的工程应用方面具有潜在的优势。
为了将高阶精度格式应用于工程实际问题，还要有可以接受的计算效率。计算效率除受空间离散格式影响外，更主要受时间推进方法影响。时间推进方法可分为显式和隐式两类。显式方法受CFL条件限制，计算效率较低。与显式方法比较，隐式方法具有更高的效率。因此，在CFD应用技术研究中得到了更多的关注，发展了许多有效的隐式方法，如Beam-Warming[7]的ADI方法，Pulliam和Chaussee[8]的DADI方法，Bardina和Lombard[9]的DDADI方法，Klopfer和Hung[10]等的D3ADI方法，Jameson和Turkel[11]的LU方法，Yoon和Jameson[12]的LU-SGS方法，Fujii和Obayashi[13]的LU-ADI方法，Briley和Neerarambam[14]的LU-AF方法，Chen和Wang[15]的BLU_SGS方法，Jameson和Caughey[16]的SGS-Newton迭代方法，MacCormack的GSLR[17]，Reddy等[18, 19]的GSPR方法等。这些方法在二阶精度的CFD计算中取得了很好的效果。但是，将这些在二阶精度计算中发展的隐式时间推进方法直接应用于高阶精度计算，存在一个适应性问题。比如，LU-SGS方法构造简单，在二阶精度计算中具有良好的稳定性和收敛性，因此得到了广泛的应用，但是将其应用于WCNS高阶精度格式上效果就不太理想。究其原因，离散方程左端项的精度低，特别当右端项采用高阶精度格式离散时造成左、右两端离散精度不匹配影响了收敛速度[10, 15]。针对这个问题，文献[20]研究了LU-SGS、点松弛、线松弛以及 GMRES四种方法应用于WCNS-E高阶精度格式上的适应性问题。其高超声速数值试验表明，与LU-SGS相比，采用准确雅克比矩阵的松弛法可以显著提高高阶精度格式的收敛速度。从而证实了提高离散方程左端项的精度可以达到提高收敛速度的目的。
众所周知，流动控制方程和CFD方法在不同的速度范围具有不同的特性和表现。比如，低速问题受所谓“刚性”的影响，如果不采用特殊处理(比如，预处理技术)，其计算效率往往比较低。而对于跨声速问题，控制方程性质处于跨界状态，有激波与边界层干扰，流场对很多因素都比较敏感，历来是CFD计算的难点。低速和跨声速问题不但非常典型，而且具有广泛的工程背景。另一方面，BLU-SGS方法也采用了更准确的方式分裂雅克比矩阵，在二阶精度计算中表现很优秀。所以，本文针对低速流动问题，重点研究BLU-SGS方法应用到WCNS-E高阶精度格式上的收敛效率问题，并与LU-SGS方法进行比较。
1 计算方法 1.1 时间推进方法对非定常雷诺平均的Navier-Stokes方程(URANS)在时间方向上进行隐式离散，非定常项采用一阶后向差分，其它项采用一阶泰勒展开，并令δQ=Qn+1－Qn，δEv=Evn+1－Evn，得：
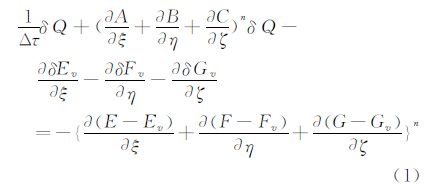
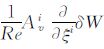，Tw=∂Q/∂W，则：
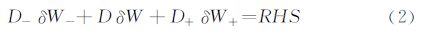
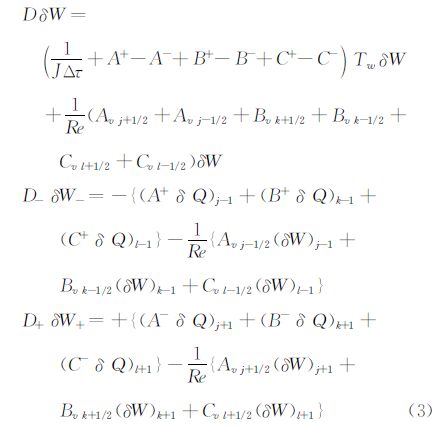
对于离散方程(3)可以采用不同的方法进行求解。本文采用BLU-SGS和LU-SGS两种隐式方法进行迭代求解。采用BLU-SGS时，A±=$\frac{1}{2}$(A±β|A|)，Av采用完整形式的雅克比矩阵，因此D为 一个5×5矩阵，具体方法参见文献[15]。采用LU-SGS时，A±=$\frac{1}{2}$(A±βrA))，rA为A的谱半径，Av只取对角项，因此D为对角矩阵，具体方法参见文献[12]。
1.2 空间离散方法对于式(1)右端项的离散，对流项采用具有五阶空间离散精度的WCNS-E格式，粘性项采用基于节点/半节点交错方法的六阶中心型差分。 1.2.1 对流项的离散
对流项采用具有五阶空间离散精度的WCNS-E格式离散，以∂E/∂ξ为例：
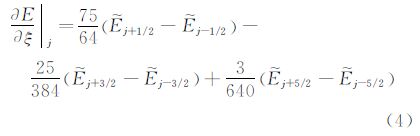
粘性通量采用与无粘通量相同的六阶中心型格式(4)进行离散，其中粘性通量$\tilde{E}$v j+1/2包含的半节点处的原始变量通过插值得到，一阶导数通过六阶中心型差分格式计算。
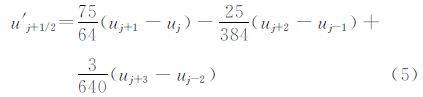
湍流模型选择k-ω SST两方程模型，采用与RANS方程相同的方法进行离散。即对流项采用WCNS-E五阶格式离散，耗散项采用六阶中心型差分格式离散；湍流模型离散方程的求解方法选择1.1节的BLU-SGS或LU-SGS方法，流动控制方程与湍流模型方程采用松耦合方式迭代求解。
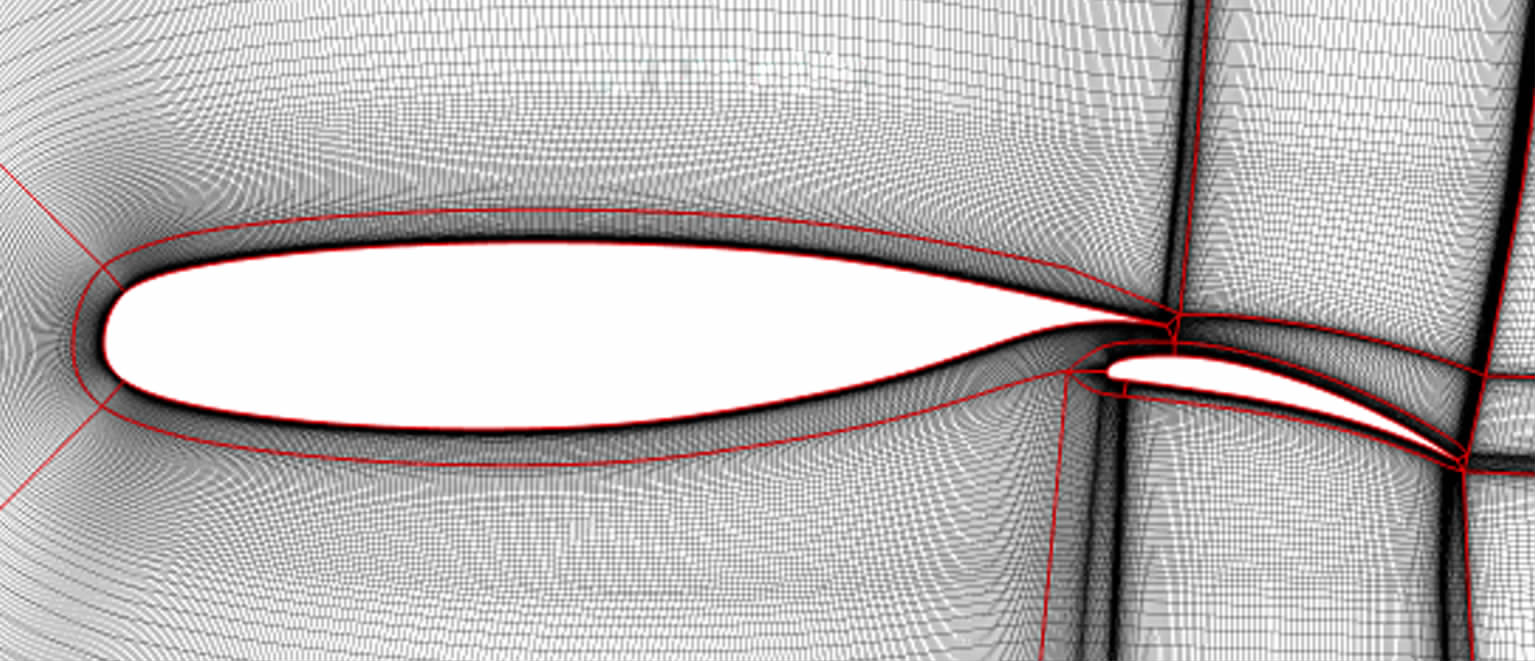
2 NLR7301两段翼型数值模拟 2.1 NLR7301两段翼型外形及网格NLR7301两段翼型由主翼和襟翼组成，襟翼偏角为20°，主翼和襟翼之间的间隙宽度为0.026c (c为弦长)，重叠区域长度为0.053c(CFG.2)。计算网格如图 1所示，多块对接网格，网格单元数为191 376，第一层壁面距离5×10－6c。
|
| 图 1 NLR7301计算网格 Fig. 1 Computational mesh of NLR7301 |
计算状态：M∞=0.185，α=13.1°，Re=2.51×106(基于平均气动弦长)。
2.2.1 收敛效率图 2比较了BLU-SGS和LU-SGS两种求解方法的残差和升力系数和阻力系数的收敛情况。从图 2中可见，两种求解算法的气动力收敛结果是一致的，BLU-SGS算法的残差收敛更佳；得到收敛的气动力系数的迭代步数比LU-SGS节约50%，虽然单步CPU时间前者要多15%左右，但是对总CPU时间而言BLU-SGS算法仍具有明显优势。
|
| 图 2 NLR7301翼型的收敛性历程曲线 Fig. 2 Convergence histories of NLR7301 airfoil |
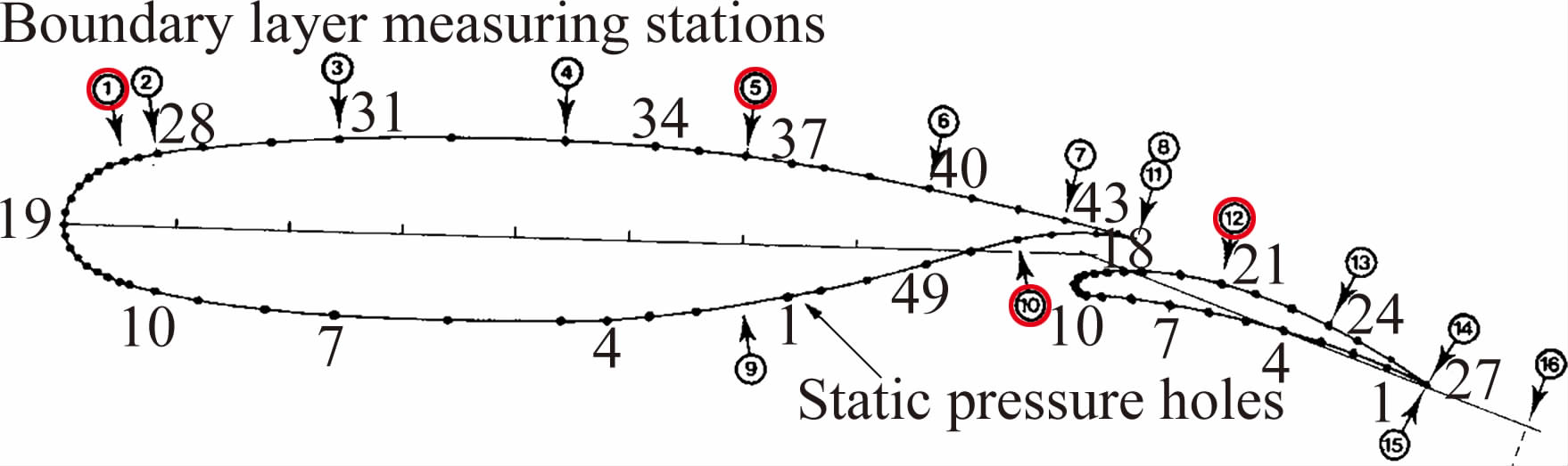
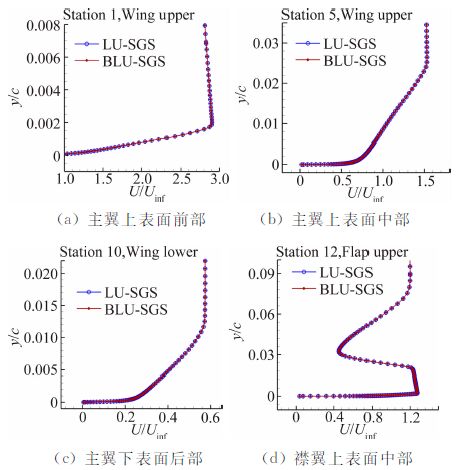
图 3给出了NLR7301两段翼型四个典型站位的示意图，主翼上表面前部、主翼上表面中部、主翼下表面后部和襟翼上表面中部分别位于层流区域、湍流充分发展区域和尾迹影响区域。图 4比较了BLU-SGS和LU-SGS两种方法在这四个站位上的速度型分布，二者给出了完全重合的结果。
|
| 图 3 NLR7301翼型边界层测量站位示意图 Fig. 3 Boundary layer measuring stations of NLR7301airfoil |
|
| 图 4 NLR7301典型站位边界层速度型 Fig. 4 Typical velocity profiles for boundary layer of NLR7301 airfoil |
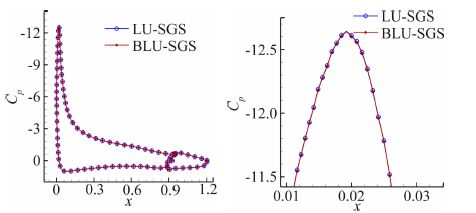
图 5给出了BLU-SGS和LU-SGS两种方法得到的表面压力分布及局部放大图，二者是一致的。
|
| 图 5 NLR7301翼型表面压力分布 Fig. 5 Distribution of pressure coefficent for NLR7301 airfoil |
表 1给出的采用两种求解方法得到气动力系数及相应的试验结果[21]，其中CDf为摩擦阻力系数、CDp为压差阻力系数。
| CL | CD | Cm | CDf | CDp | |
| LU-SGS | 3.121 | 0.0552 | -0.449 | 0.0085 | 0.0468 |
| BLU-SGS | 3.120 | 0.0550 | -0.449 | 0.0085 | 0.0466 |
| Experiment | 3.141 | 0.0445 | / | / | / |
从表 1看出，BLU-SGS和LU-SGS两种方法的结果没有明显的差异，不同的隐式迭代方法对升力系数和阻力系数的影响非常小。采用转捩模型可以进一步提高计阻力系数与试验结果的吻合程度[22]。
3 Trap Wing 梯形翼数值模拟 3.1 Trap Wing 梯形翼构型及网格梯形翼高升力构型是安装在机身上的大弦长、中等展弦比、前缘缝翼/主机翼/后缘襟翼三段构型，机翼无扭转、无上反角，前缘缝翼偏角为30°，后缘襟翼偏角为25°(CFG.1)，半展长为2.1604m，平均气动弦长1.0067m。计算网格如图 6所示，为多块对接网格，网格单元数为14 645 760，第一层法向网格壁面距离4×10－6。
|
| 图 6 梯形翼构型计算网格 Fig. 6 Computational grid for trap wing configuration |
计算状态：M∞=0.2，α=13°，Re=4.3×106(基于平均气动弦长)。
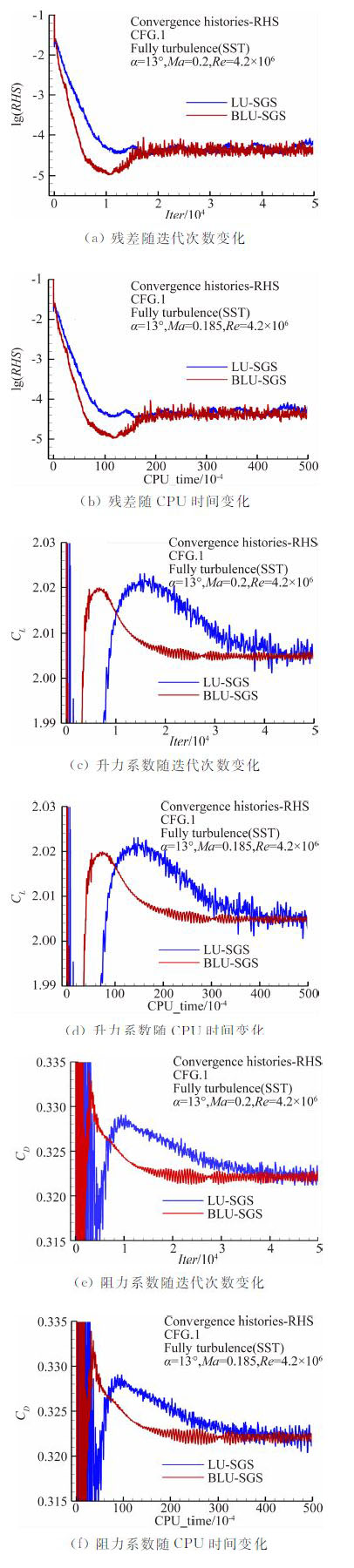
3.2.1 收敛效率图 7比较了BLU-SGS和LU-SGS两种方法的残差和气动力系数的收敛情况。与二维NLR7301的表现一致： 两种求解算法的气动力收敛结果是一致的，BLU-SGS算法的气动力力系数波动更小；从迭代步数和总CPU时间来看，BLU-SGS算法都具有明显的优势。残差及气动力系数的波动是由流场中的局部分离引起的。
|
| 图 7 梯形翼构型气动力系数的收敛性历程曲线 Fig. 7 Convergence histories of aerodynamic characteristics of trap wing configuration |
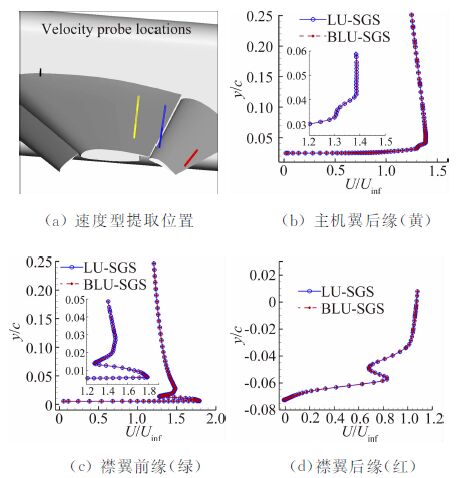
图 8给出了边界层内三个典型站位上的速度型分布，分别位于主机翼后缘、襟翼前缘和襟翼后缘，都在靠近翼梢的上表面上。从图 8可见，BLU-SGS和LU-SGS两种方法给出了相同的结果，在这三个站位上的速度型都是重合的。
|
| 图 8 高升力构型典型站位边界层速度型 Fig. 8 Typical velocity profiles for boundary layer of trap wing configuration |
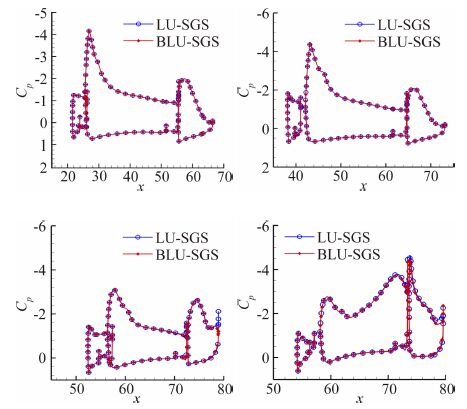
图 9给出了BLU-SGS和LU-SGS两种求解方法得到的梯形翼构型典型展向站位的表面压力分布曲线。在位于机翼中部的η=0.41和η=0.70位置，两种求解方法的表面压力分布是完全一致的；在位于翼梢附近的η=0.95和η=0.98位置，缝翼和主机翼上的表面压力分布也保持了一致性，只是在襟翼上表面特别是襟翼后缘存在微小差异。
|
| 图 9 高升力构型表面压力分布 Fig. 9 Distribution of pressure coefficent for trap-wing |
表 2给出了采用两种隐式求解方法得到的梯形翼构型的气动力系数及相应的试验结果[23]。
| CL | CD | Cm | CDf | CDp | |
| LU-SGS | 2.0045 | 0.3219 | -0.4761 | 0.0118 | 0.3101 |
| BLU-SGS | 2.0048 | 0.3221 | -0.4762 | 0.0118 | 0.3103 |
| Experiment | 2.0468 | 0.3330 | -0.5032 | / | / |
从表 2给出的气动力系数来看，两种隐式求解方法的结果没有明显的差异，不同的时间推进方法对气动力系数的影响非常小。
4 结 论通过NLR-7301两段翼型和Trap Wing梯形翼两个低速构型的算例分析，可以得出以下结论：
(1) BLU-SGS的收敛特性显著优于LU-SGS，残差下降更快。
(2) 对收敛的流场，BLU-SGS方法与LU-SGS方法的计算结果基本相同，不同隐式迭代方法对计算结果影响很小。
本项研究的下一步工作将采用高阶精度计算方法，针对跨声速构型开展BLU-SGS方法的收敛效率研究。
| [1] | Deng X G, Maekawa H. Compact high-order accurate nonlinear schemes[J]. J. Comp. Phys., 1997, 130:77-91. |
| [2] | Deng X G, Mao M L, Weighted compact high-order nonlinear schemes for the euler equations[R]. AIAA 97-1941. |
| [3] | [KG2.6mm]Deng X G, Zhang H X. Developing high-order weighted compact nonlinear schemes[J]. J. Comp. Phys., 2000, 166:22-44. |
| [4] | Deng X G. High-order accurate weighted compact nonlinear schemes[J]. Science in China, Ser. A, 2001, 31(12):1104-1117.邓小刚,高阶精度耗散加权紧致非线性格式[J].中国科学(A辑), 2001, 31(12):1104-1117. |
| [5] | Deng X G, Liu X, Mao M L, et al. Advances in high-order accurate weighted compact nonlinear schemes[J]. Advances in Mechanics, 2007, 37(3):417-427.邓小刚,刘欣,毛枚良,等.高精度格式加权紧致非线性格式的研究进展[J].力学进展, 2007, 37(3):417-427. |
| [6] | Deng X G, Mao M L, Tu G H, et al. Geometric conservation law and applications to high-order finite difference schemes with stationary grids[J]. J. Comp. Phys., 2011, 230:1100-1115. |
| [7] | Beam R, Warming R F. An implicit factored scheme for the compressible Navier-Stokes equations[J]. AIAA Journal, 1978, 16:393-402. |
| [8] | Pulliam T H, Chaussee D S. A diagonal form of an implicit approximate factorization algorithm[J]. J. Comp. Phys., 1981, 39(2):347-363. |
| [9] | Bardina B S, Lombard H. Three dimension hypersonic flow simulations with the CSCM implicit upwind Navier-Stokes equations[R]. AIAA 87-1114. |
| [10] | Klopfer G H, Hung C M, Van der Wijgaart R F, et al. A diagonalized diagonal dominant alternating direction implicit (D3ADI) scheme and subiteration correction[R]. AIAA 98-2824. |
| [11] | Jameson A, Turkel E. Implicit schemes and L-U decompositions[J]. Mathematics of Computation, 1981, 37(156):385-397. |
| [12] | Yoon S, Jameson A. Lower-upper symmetric gauss-seidel method for the Euler and Navier-Stokes equations[J]. AIAA J., 1988, 26:1025-1026. |
| [13] | Fujii K, Obayashi S. Computation of three-dimensional viscous transonic flows using the LU-ADI factored scheme[R]. NAL-TR-899T, 1986. |
| [14] | Briley W R, Neerarambam S S, Whitfield D L. Implicit lower-upper/approximate-factorization schemes for incompressible flows[J]. J. Comp. Phys., 1996, 128:32-42. |
| [15] | Chen R F, Wang Z J. Fast, block lower-upper symmetric gauss-seidel scheme for arbitrary grids[J]. AIAA Journal, 2000, 38(12):2238-2245. |
| [16] | Jameson A, Caughey D A. How many steps are required to solve the Euler equations of steady, compressible flow:in search of a fast solution algorithm[R]. AIAA 2001-2673. |
| [17] | MacCormack R W. Current status of numerical solutions of the Navier-Stokes equations[R]. AIAA 85-0032. |
| [18] | Reddy K C, Jacocks J L. A locally implicit scheme for the Euler equation[R]. AIAA 87-1144. |
| [19] | Reddy K C, Benek J A. A locally implicit scheme for 3-D compressible viscous flows[R]. AIAA 90-1525. |
| [20] | Zhang Y F. Investigations of convergence acceleration and complex flow numerical simulation for high-order accurate scheme (WCNS)[D]. China Aerodynamics Research and Development Center, 2007.张毅锋.高阶精度格式(WCNS)加速收敛和复杂流动数值模拟的应用研究[D].中国空气动力研究与发展中心, 2007. |
| [21] | Van Den Berg B. Boundary Layer measurements on a two-dimensional wing with flap[R]. NLR-TR-79009 U. Amsterdam:NLR, 1979. |
| [22] | Wang Y T, Zhang Y L, Li S, et al. Calibration of a γ-Reθ transition model and its validation in low-speed flows with high-order numerical method[J]. Chinese Journal of Aeronautics, 2015, 28(3):704-711. |
| [23] | Johnson P L, Jones K M, Madson M D. Experimental Investigation of a simplified 3D high lift configuration of civil transport aircraft[R]. AIAA 2008-410. Reston:AIAA, 2008. |