2. 南京航空航天大学航空宇航学院, 江苏南京 210016
2. College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China
0 引 言
随着计算机计算能力的提升与计算技术的发展,CFD(计算流体动力学)软件已经成为流场分析、流场计算、流场预测的重要工具。在翼型气动优化过程中,由于需要在翼型设计空间大量调用高精度流场计算模拟,基于CFD的优化计算会受到时间、财力的限制。一个解决方案是采用代理模型[1]技术(又称响应面技术)构建近似模型来代替复杂的CFD计算。近似模型描述了目标函数(输出)与设计变量(输入)之间对应关系。通过近似模型计算目标函数值节省了大量计算时间并且可以搜索更广阔的设计空间。一些试验表明基于代理模型的优化技术不仅高效而且可靠,已逐渐在工程上得到应用[2, 3, 4, 5]。
翼型设计领域中常用的代理模型主要有多项式模型,人工神经网络模型,Kriging模型(单输出高斯回归模型)[3, 4, 5, 6]等。高斯过程回归模型本质上是一种基于贝叶斯框架的回归方法,有着严格的统计学理论基础。高斯模型能很好地处理小样本、非线性等复杂的问题。利用统计学方法来寻找输入变量与输出变量之间的条件分布,从而建立两者的回归方程。高斯回归模型分为单输出高斯过程(Single Output Gaussian Process,即Kriging)回归模型[7]和多输出高斯过程(Multiple Output Gaussian Process,MOGP)回归模型[8, 9]。单输出模型对每个输出端口分别建模,忽略了端口之间的潜在相关性。MOGP回归模型则为各个输出端口之间建立了协方差矩阵来模拟它们之间可能存在的依赖关系,每个端口都可以利用其它输出端口来提升自己的预测性能。
在先前的工作中,我们验证了MOGP模型相比Kriging模型在多响应之间存在显著相关性时,能进一步提高代理模型在超临界翼型设计中的预测精度[10]。本文将CST参数化方法、MOGP多响应代理模型与模拟退火算法相结合设计了一种翼型优化设计方法,并将该方法应用到超临界翼型的优化设计中。通过单点和多点两个翼型优化算例证明了提出方法的有效性。
1 多输出高斯过程模型MOGP设含有D个函数的集合,{fd(x)}d=1D,其中每一个函数都可以被表示成一个光滑核函数,{Gd(x)}d=1D,和一个隐含函数u(x)的卷积,即:
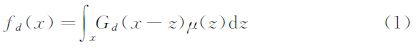
更一般的,可以认为每一个光滑核函数和隐函数都是由若干个子函数线性组合而成,
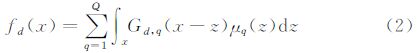
每一个子函数都拥有相同的协方差函数,且相互独立。
多输出高斯过程卷积的光滑核函数和隐函数的选择有多种,但在实际应用中,一般采取高斯形式,使光滑核函数和隐函数拥有相同的高斯形式,其可行性已由Boyle和Frean证明[8],光滑核函数表示为:
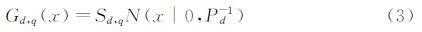
隐含过程的协方差函数可以表示为:
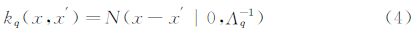
在上面的表达式中,Λq是关于隐函数的精度矩阵。于是我们可以得到任意两个输出端口的协方差表达式:
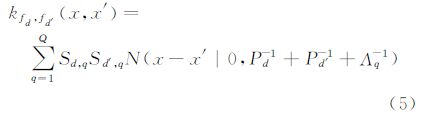
给定卷积形式之后,模型的似然函数表示为:
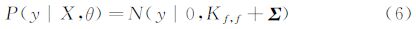
给定新的输入集合X*后,模型输出的预测分布为:
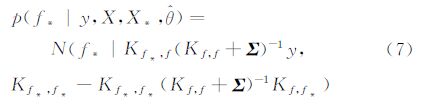
由于式(7)的协方差矩阵Kf,f表示的是所有输出数据的协方差,所以MOGP可以为多输出建模,能够模拟多输出端口之间的相关性。
2 CST翼型参数化方法CST方法[11, 12, 13]是近年提出的一种可以使用较少的设计变量来精确描述复杂几何外形的翼型参数化方法。该方法通过类函数定义了要描述的一般的几何外形,型函数用来描述给定类函数的特性,具有设计变量可调节、设计空间广等优点。本文采用CST参数化方法对超临界翼型进行建模。
用CST参数化方法表示翼型的数学公式为:
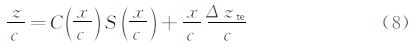
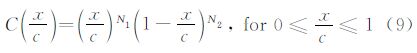
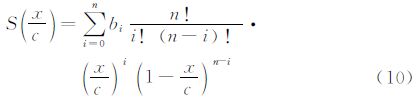
对于C(x/c),当N1、N2取不同的值时,可以定义不同分类的基本几何形状。本文中取N1、N2分别为0.5和1.0,方程(8)右边的第一项和第二项分别表示翼型的圆前缘和尖后缘,以保证参数化在翼型的轴向极值处具有很好的数学特性。
在方程(10)中,多项式系数{bi}表示了对给定翼型的设计变量,称之为Bernstein系数,用以生成更复杂更实用的翼型,可通过最小二乘法拟合翼型得到。
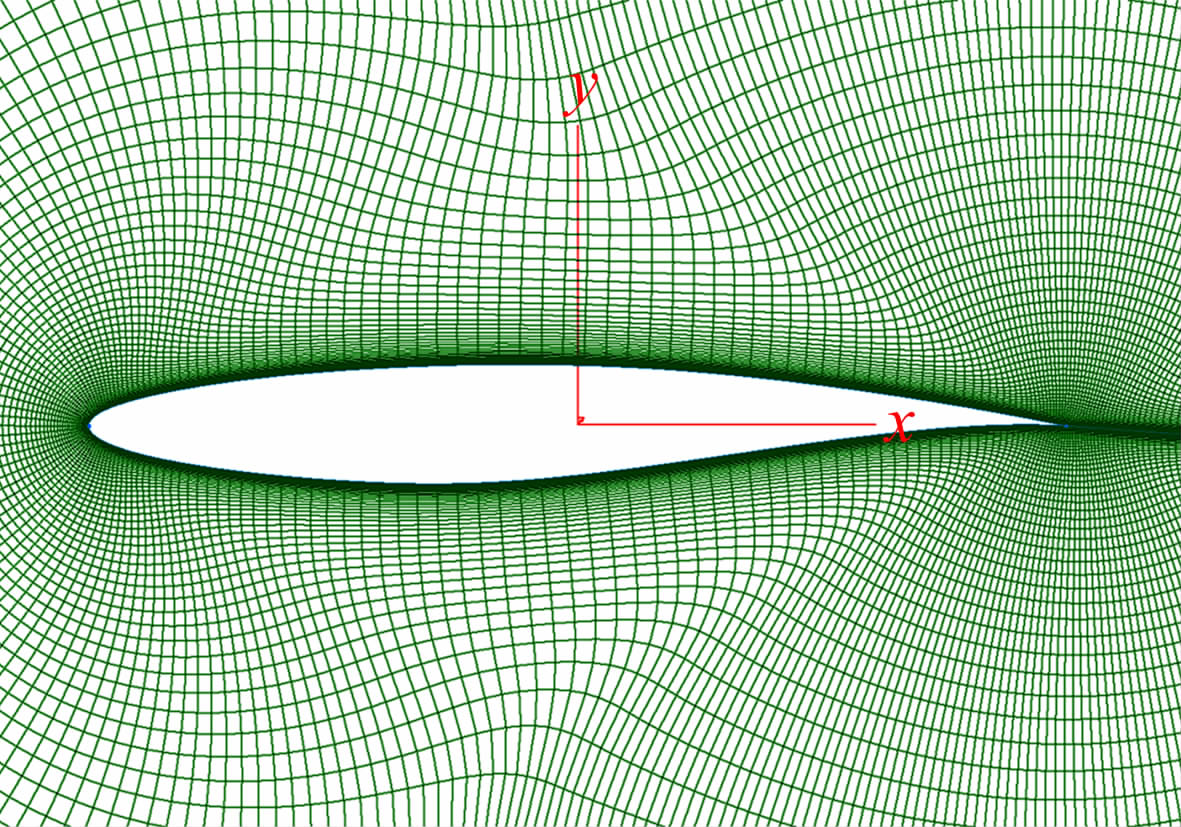
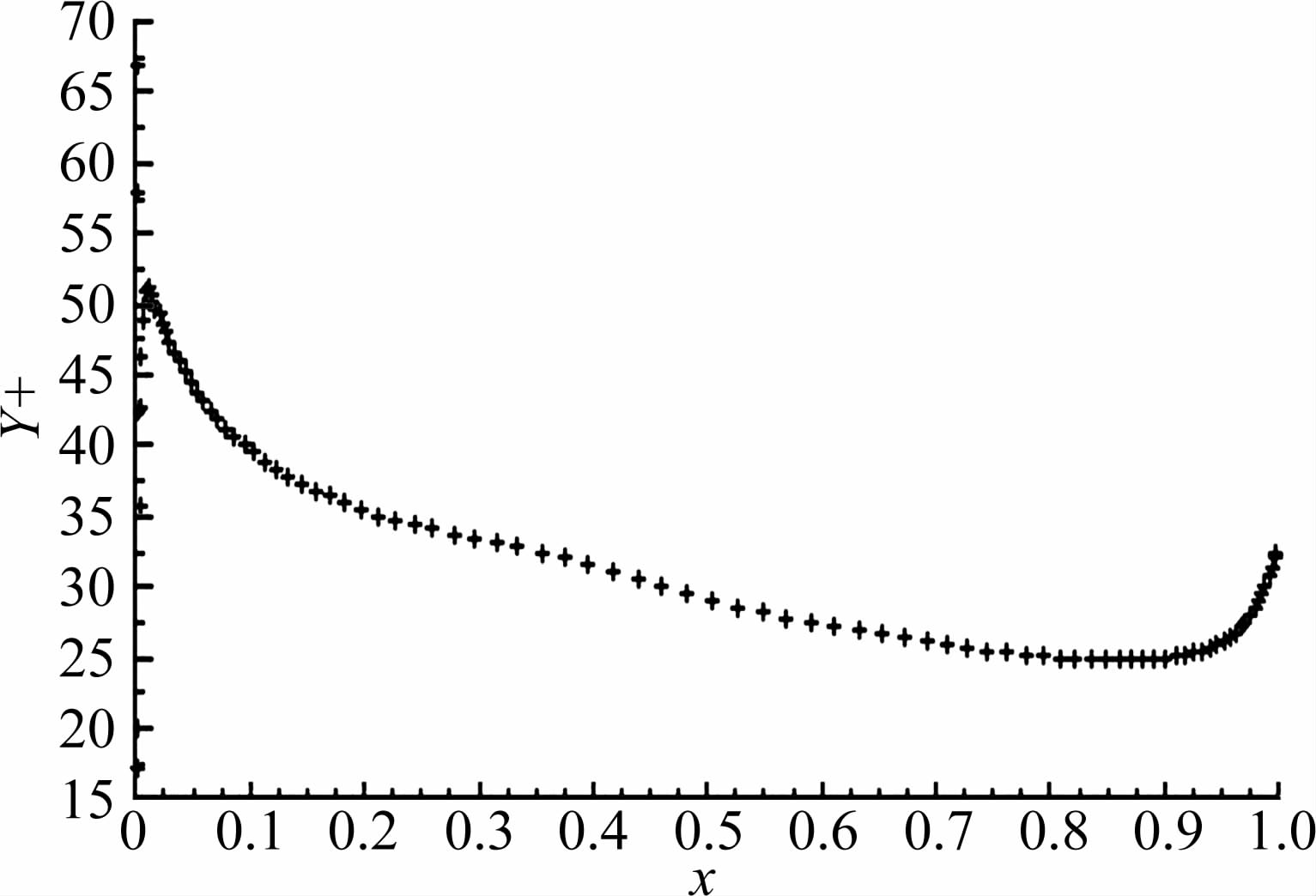
3 CFD分析方法流场控制方程采用守恒形式的N-S方程。N-S方程空间离散采用有限体积方法,对流通量采用Roe通量差分格式,湍流模型采用了κ-ε模型。采用粘性网格,网格在整个流场范围内的规模为387×104个单元,图 1 表示了RAE2822翼型网格拓扑结构。图 2 表示了该网格的Y+分布。
|
| 图 1 RAE2822的网格图示 Fig. 1 Grid for RAE2822 |
|
| 图 2 翼型RAE2822网格的Y+分布 Fig. 2 Y+ distribution of RAE2822 |
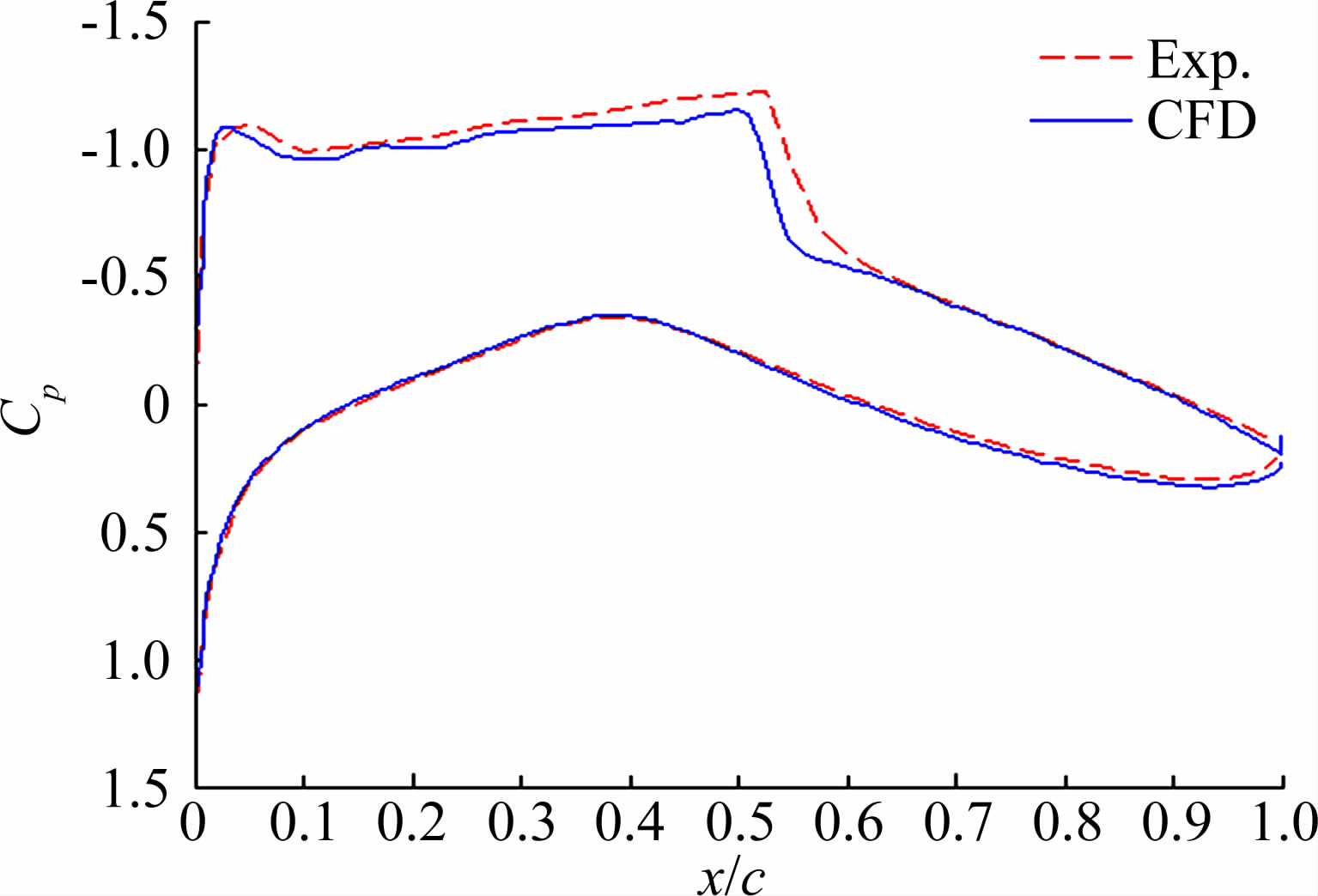
为了验证计算程序的准确性,图 3给出了RAE2822翼型马赫数0.729,迎角2.31°状态下计算与试验压力分布对比。可以看出,CFD计算与试验结果吻合较好,能够准确捕捉到上翼面的激波。
|
| 图 3 压力分布比较 Fig. 3 Comparison of pressure coefficient distributions |
模拟退火算法[14](Simulated Annealing,SA)的思想来源于热力学中对固体退火过程的模拟,将固体加温至融化,再让其徐徐冷却凝固成晶体。加温时,固体内部粒子随者温度升高处于不稳定状态,内能增大,而温度缓慢下降时,粒子内能减小,固体内部状态趋于稳定。在实际应用中,将温度t作模拟为控制参数,将内能模拟为目标函数值f,对于控制参数t的每一个取值,算法持续进行“产生——新解——判断——接受或舍弃”的迭代过程,并逐步衰减t值,算法终止时的当前解记为所得近似最优解。其中,使用Metroplis准则作为判断当前解是否为新解替换的标准。这是基于蒙特卡罗迭代算法的一种启发式随机搜索过程。模拟退火算法适合处理传统搜索方法难以解决的高度复杂的非线性问题。本文采用模拟退火算法作为翼型设计的优化算法。
5 翼型优化系统 5.1 试验设计试验设计的目的是选择一些有代表性的样本点从而利用少量试验点得到较高精度的代理模型。试验设计的方法有多种,但主要有正交试验设计、均匀设计、中心复合设计和拉丁超立方设计等。拉丁超立方设计[15](Latin Hypercube Sampling,LHS)是满足空间试验设计中一种较为优秀的试验设计方法,现在已经获得了广泛的应用。因此本文选用拉丁超立方设计来选取所需要的样本点。
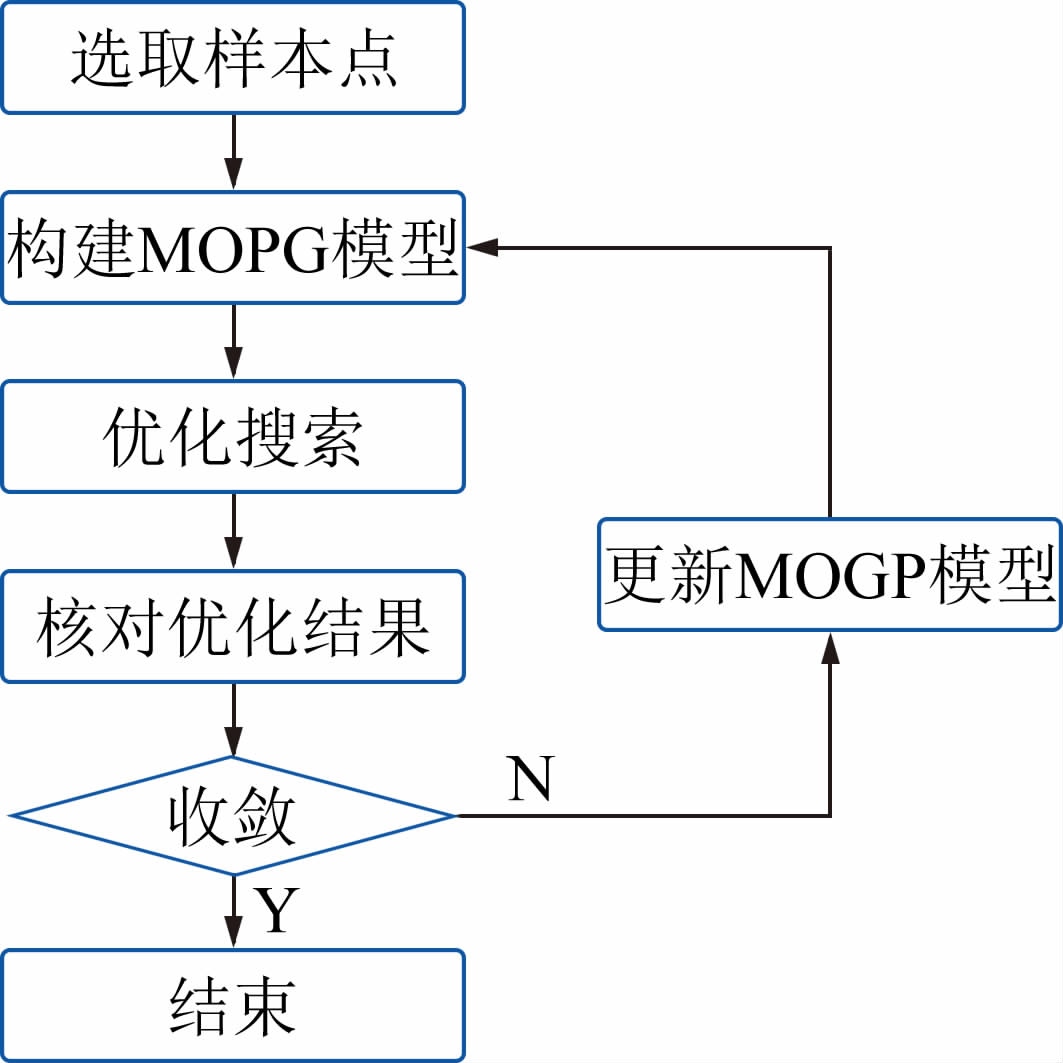
5.2 翼型优化设计算法框架基于MOGP多响应代理模型的翼型优化设计方法的步骤为:首先确立使用数学语言描述的优化目标,通过CST参数化方法确定合理的翼型设计空间(设计变量的个数及其取值范围);然后采用拉丁超立方抽样在设计空间内选取合适的初始样本点,并使用CFD软件计算出初始翼型所对应的响应值(升力系数、阻力系数等);根据初始样本点信息构造MOGP模型;根据初始样本点构造MOGP代理模型。对代理模型进行优化分析,翼型的几何约束采用罚函数法[16]处理,即对违反约束的个体适应度施加一个惩罚项,使用模拟退火算法寻找最佳的设计变量取值,对搜索到的局部最优值,将它加入到初始样本点中,重新构造模型,如此迭代计算,直到收敛到全局最优点。图 4是基于MOGP模型与模拟退火算法的优化流程图。
|
| 图 4 优化流程图 Fig. 4 Flow chart of optimization |
6.1 单点翼型优化设计
算例1。以超临界翼型RAE2822为初始翼型,以面积、升力等作为约束条件,进行单目标减阻优化设计,设计状态为迎角2.79°,马赫数0.734,雷诺数6.5×106。优化问题可以描述为:
Minimize CD
Subject to CL=0.7983
Area≥0.99Area0
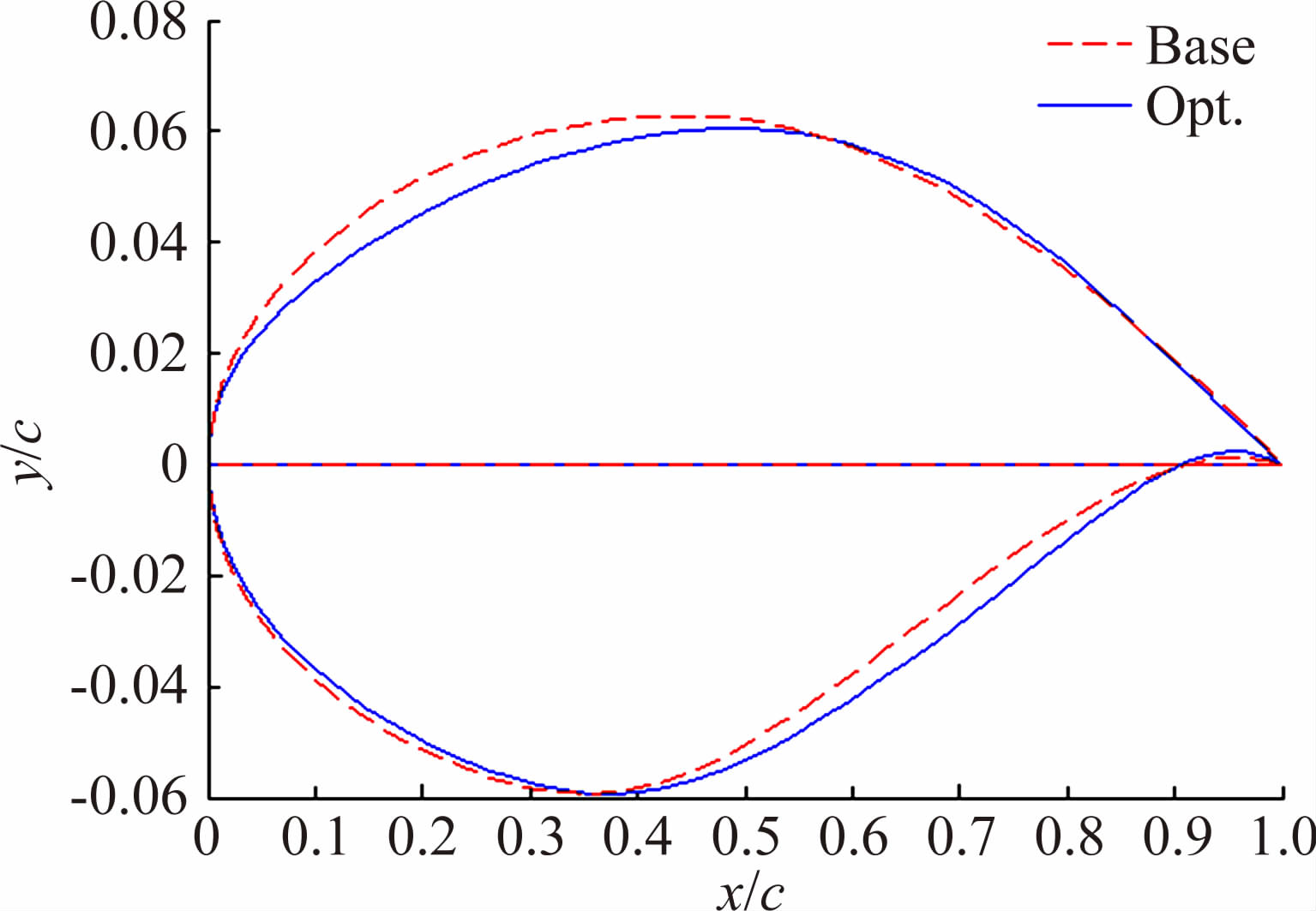
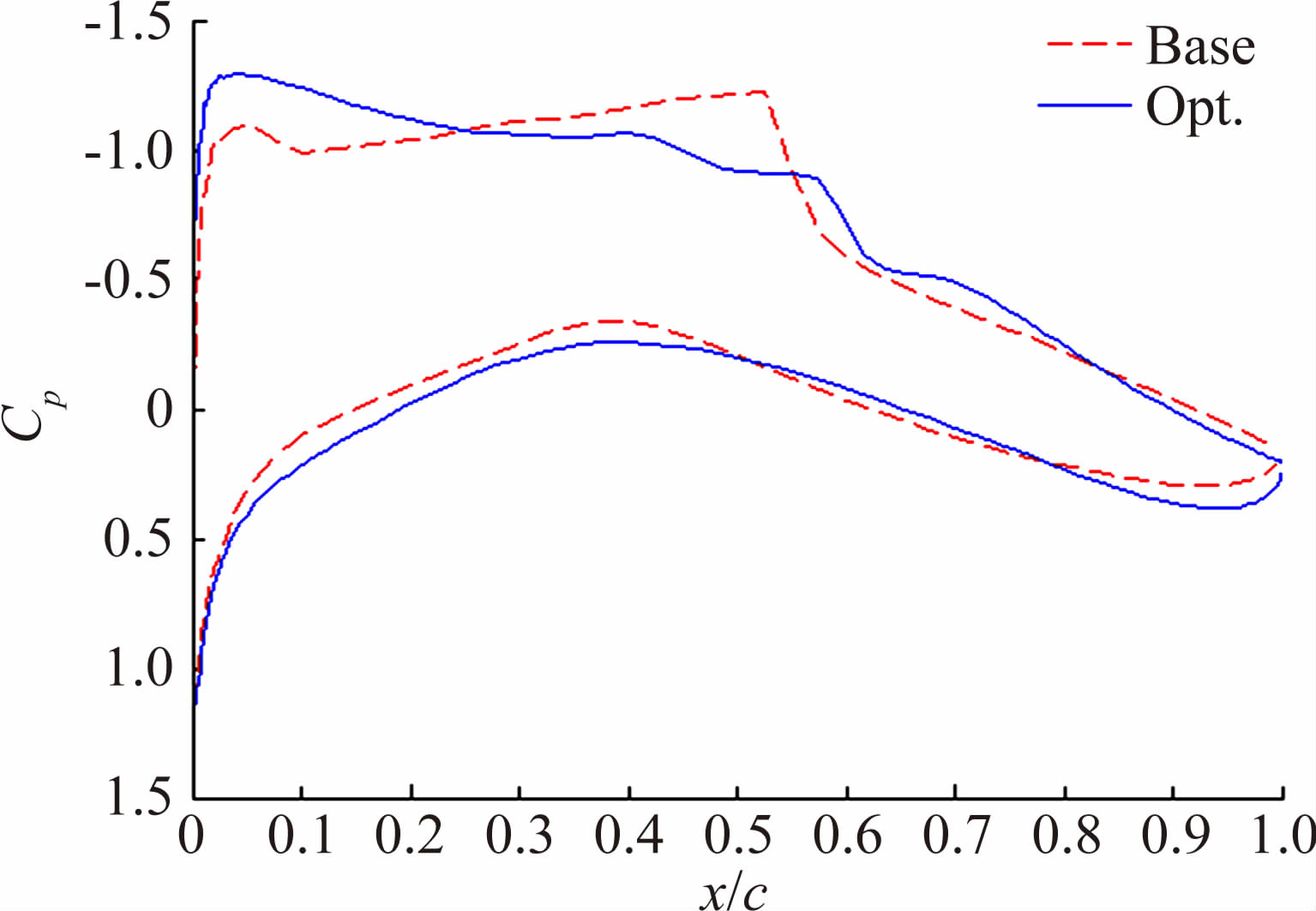
在优化设计过程中,取12维Bernstein系数作为设计变量,在给定的设计变量约束范围内,采用拉丁超立方抽样选取121个初始试验点,建立初始MOGP模型,通过模拟退火算法得到单次搜索最优解并加入原样本集中,经过21次循环后得到最终最优解。表 1给出了设计变量范围与最终优化结果,表 2给出了基准翼型和优化后翼型的气动力参数比较。由表可知,在满足约束条件的前提下,优化后的翼型阻力系数比基准翼型减小了31%。图 5和图 6分别给出了原始外形与最终优化得到的翼型的形状以及压力分布的比较。由图可知,优化翼型有着较小的前缘半径,并且翼型的激波有着明显的减小。
| 设计变量 | 约束范围 | 优化结果 |
| b0 | [0.06,0.18] | 0.1018 |
| b1 | [0.09,0.20] | 0.1244 |
| b2 | [0.06,0.24] | 0.1473 |
| b3 | [0.10,0.30] | 0.1836 |
| b4 | [0.04,0.34] | 0.2583 |
| b5 | [-0.01,0.40] | 0.1233 |
| b6 | [0.06,0.18] | 0.1243 |
| b7 | [0.04,0.16] | 0.1321 |
| b8 | [0.09,0.28] | 0.2149 |
| b9 | [0,0.22] | 0.1050 |
| b10 | [-0.14,0.22] | 0.1522 |
| b11 | [-0.23,0.20] | -0.1086 |
| 翼型 | CD | CL | Area |
| 基准翼型 | 0.0185 | 0.7983 | 0.0778 |
| 优化翼型 | 0.0127 | 0.8054 | 0.0770 |
|
| 图 5 优化前后翼型形状 Fig. 5 Comparison between initial and optimized airfoil configurations |
|
| 图 6 优化前后翼型表面压力分布比较 Fig. 6 Comparison of airfoil pressure distribution between initial and optimized airfoil |
飞行器需要在一定的马赫范围内均有良好的性能。通常只有一个设计状态的单点优化很难满足要求,而多目标优化可以有效地将多个设计要求统一起来处理。这里我们对RAE2822翼型在马赫数0.70和0.75进行两点优化,并考察优化翼型在马赫数范围0.68至0.76内,阻力系数的发散情况。
对于多目标的优化问题,采用“统一目标函数法”[17, 18, 19]处理多目标函数。统一目标函数法,即将各个分目标函数统一到一个总的目标函数中去。在两点翼型优化中,假设第一设计点和第二设计点的目标函数分别为F1(x)、F2(x),使用线性插值法将各个分目标函数规格化为:


本文中,目标函数F1(x)、F2(x)分别代表待优化翼型在低马赫数与高马赫数下的气动性能参数,其权重是相同的,我们令加权因子ω1、ω2均为0.5。
算例2。设计状态(1):迎角2.79°,马赫数0.70,雷诺数6.5×106;设计状态(2):迎角2.79°,马赫数0.75,雷诺数6.5×106。
Minimize CD1,CD2
Subject to CL1=0.7526
CL2=0.7858
算例2采用了242个初始样本点构造MOGP代理模型,表 3、表 4给出了优化结果。经过优化后,优化翼型在两个设计状态下,阻力系数比基准翼型分别减小了5.5%和23%。
| CD | CL | |
| 基本翼型 | 0.0110 | 0.7526 |
| 优化翼型 | 0.0104 | 0.7534 |
| CD | CL | |
| 基本翼型 | 0.02502 | 0.7858 |
| 优化翼型 | 0.01920 | 0.8080 |
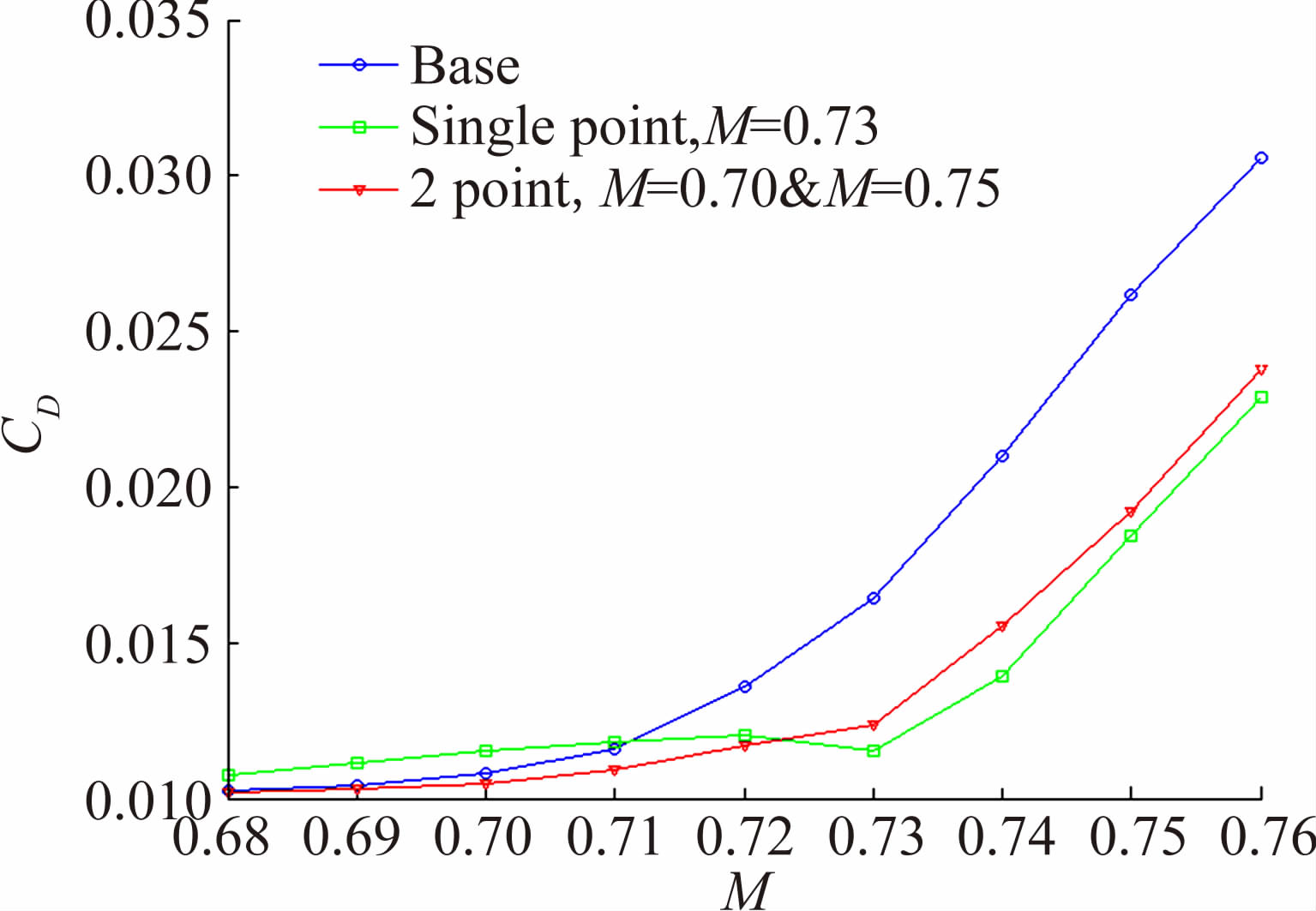
图 7给出了优化前后的阻力发散特性。从图 7中可以看到,由于单点优化只是局部地优化了一个设计点(Ma=0.73)的气动性能,所以优化后的翼型虽然在设计点处和高马赫区域取得了良好的减阻效果,却较为严重地恶化了低马赫数条件下翼型的阻力特性。而多目标优化在设计点Ma=0.70(低马赫数区域)和设计点Ma=0.75(高马赫数区域)进行了全局的优化,所以优化后的翼型在给定的马赫数范围0.68至0.76内都有良好的减阻效果,极大地提高了阻力发散特性。
|
| 图 7 翼型单点与多点优化阻力特性比较 Fig. 7 Drag character of airfoil at different optimization result |
本文设计了一种基于机器学习算法和传统优化算法相结合的优化方法,并用于超临界翼型的优化设计。其核心部分为采用训练后的MOPG模型作为气动性能评估的代理模型,优化算法采用的是模拟退火算法。根据所采用的优化算例可以看出,基于MOGP模型的优化设计方法有效地改善了初始基准翼型的气动性能。从优化设计压力分布来看,所采用的优化方法能给出合理的翼型,并给出期望的压力分布。优化结果表明,所发展翼型优化设计方法可以有效地应用于超临界翼型的多目标气动优化设计,有着较好的工程应用前景。
| [1] | Pena F L, Casás V D, Gosset A, et al. A surrogate method based on the enhancement of low fidelity computational fluid dynamics approximations by artificial neural networks[J]. Computers and Fluids, 2012, 58:112-119. |
| [2] | Hacioglu A. Fast evolutionary algorithm for airfoil design via neural network[J]. AIAA Journal, 2007, 45(9):2196-2203. |
| [3] | Tao Y, Li Y H, Huang Y. Multi-point optimization of supercritical airfoil based on agent model[J]. Scientific Research, System Simulation Technology & Application, 2012, (14):77-81. |
| [4] | [KG2.1mm]Han Z, Görtz S, Zimmermann R. Improving variable-fidelity surrogate modeling via gradient enhanced kriging and a generalized hybrid bridge function[J]. Aerospace Science and Technology, 2013, 25(1):177-189. |
| [5] | Jeong S, Murayama M, Yamamoto K. Efficient optimization design method using Kriging model[J]. Journal of Aircraft 2005, 42(2):413-420. |
| [6] | Ren Q Z, Song W P. Multi-objective aerodynamic design optimization for airfoil using Kriging model[J]. Aeronautical Computing Technique, 2009, 39(3):78-82. (in Chinese)任庆祝,宋文萍.基于Kriging模型的翼型多目标气动优化设计研究[J].航空计算技术, 2009, 39(3):78-82. |
| [7] | Rasmussen C E, Williams C K I. Gaussian processes for machine learning[M]. Cambridge, MA:MIT Press, 2006. |
| [8] | Boyle P, Frean M. Dependent gaussian processes[C]. Advances in Neural Information Processing Systems 17. Saul L K, Weiss Y, Bottou L, edit. Cambridge, MA:MIT Press, 2005:217-224. |
| [9] | Alvarez M A, Lawrence N D. Computationally efficient convolved multiple output Gaussian processes[J]. Journal of Machine Learning Research, 2011, (12):1425-1466. |
| [10] | Liu X, Zhu Q, Lu H. Modeling multi-response surfaces for airfoil design with multiple output gaussian process regression[J]. Journal of Aircraft, 2013. doi:10.2514/1.C032465. |
| [11] | Jacob C H, Willam A C, Gosset A. A parametric approach to supercritical airfoil design optimization[R]. AIAA Paper 2007-62. |
| [12] | Li J, Gao Z H, Huang J T, et al. Aerodynamic optimization system based on CST technique[J]. Acta Aerodynamica Sinica, 2012, 30(4):443-449. (in Chinese)李静,高正红,黄江涛,等.基于CST参数化方法气动优化设计研究[J].空气动力学学报, 2012, 30(4):443-449. |
| [13] | Kulfan B, Bussoletti J E. Fundamental parametric geometry representations for aircraft component shapes[J]. AIAA 2006-6498, 2006. |
| [14] | Xia L, Chang Y X, Zhang L. The application of an improved simulated annealing algorithm to airfoil design[J]. Flight Dynamics, 2008, 26(1):71-74. (in Chinese)夏露,常彦鑫,张龙.改进的模拟退火算法在翼型设计中的应用[J].飞行力学, 2008, 26(1):71-74. |
| [15] | Bai J Q, Wang B, Sun Z W. The research of robust supercritical airfoil design optimization[J]. Acta Aerodynamica Sinica, 2011, 29(4):459-463. (in Chinese)白俊强,王波,孙智伟.超临界翼型稳健型优化设计研究[J].空气动力学学报, 2011, 29(4):459-463. |
| [16] | Zhang L, Chen H Q. Research on genetic algorithm for aerodynamic shape optimization based on CST[J]. Aeronautical Computing Technique, 2011, 41(6):53-57. (in Chinese)张磊,陈红全.基于CST参数化的翼型优化遗传算法研究[J].航空计算技术, 2011, 41(6):53-57. |
| [17] | Zhong X P, Ding J, Li W, et al. Robust airfoil optimization with multi-objective estimation of distribution algorithm[J]. Chinese Journal of Aeronautics, 2008, 21(4):289-295. |
| [18] | Ursache N M, Bressloff N W, Keane A J. Aircraft roll enhancement via multi-objective optimization using surrogate modeling[J]. AIAA Journal, 2011, 49(7):1525-1541. |
| [19] | Yu G, Li D. Optimization design of airfoil based on hybrid genetic algorithm and compound form method[J]. ScieTechnology and Engineering, 2007, 7(10):2292-2295. |



