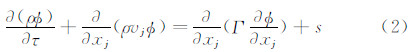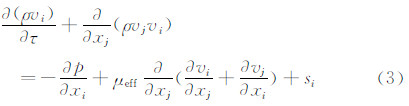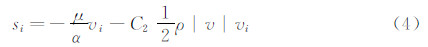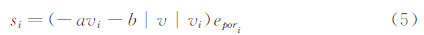0 引 言
降落伞伞衣是一种微孔透气材料，其织物透气性对降落伞的气动性能(如阻力系数、稳定性、开伞性能等)有很大的影响，由于织物透气性影响的流场模拟较为困难，风洞试验是研究降落伞气动性能和流场结构的主要方法[1, 2]。但由于降落伞伞衣一般面积很大，受风洞尺寸限制，模型伞小尺寸结构(如微孔)的缩尺效应引起的误差难以估计，因此风洞试验往往只能适用于面积较小的伞衣，应用非常有限。
早期对于降落伞绕流流场的研究是基于势流理论，Roberts在这方面做了较多工作，以此来确立伞衣面上的压力分布[3]。由于降落伞绕流存在流动分离、旋涡生成和脱落，在势流理论假设下，计算结果误差很大。考虑到绕钝体流动的流场特性，Mayer,Frucht,彭勇等人采用涡方法来计算伞形物的绕流问题[4, 5, 6, 7, 8]，涡方法对于大尺度分离流动具有自适应性强、计算量小等优点，但是由于涡的布置是人为近似确定的，这也导致计算结果的误差比较大。近年来，随着CFD技术的发展，采用基于网格的CFD技术来分析降落伞的气动特性成为各国学者研究的热点[9, 10, 11, 12, 13, 14]，该方法精度高，能精确地获得流场细节结构，具有强大的生命力和广泛的应用前景。
降落伞伞衣是一种柔性可拉伸织物微孔透气结构，若采用常规的加密网格方式处理，不仅对计算机提出了更为苛刻的要求，同时会造成其它区域很大的计算浪费，造成非常大的计算误差，甚至导致计算无法收敛，因此对织物透气性的流场模拟被认为是降落伞流场计算的关键技术问题。Tezduyar[15]将环帆伞衣分为12个同心块，对每一块的织物透气性采用几何孔隙率均匀化建模(Homogenized Modeling of Geometric Porosity)，较好的模拟了透气伞衣的全局流场特性，但孔隙率参数较难测准，使局部流场结构误差较大。Han[16]对十字形伞衣采用透气跳跃(porous jump)边界条件来模拟织物透气性，轴向力系数与实验结果比较一致，但在伞衣处出现压力阶跃，无透流速度，与实际物理现象并不完全一致。Aquelet、Tamborra、Coquet[17, 18, 19]等对降落伞流固耦合过程的织物透气性进行了模拟，将流体和固体的相对速度作为透过织物的气流速度应用于Ergun公式中得到透过织物产生的压降，以接触力形式施加到伞衣织物上，阻力系数与实验结果比较符合，但只对织物透气性进行了力等效，没有很好的模拟它对气动性能的影响。
本文建立了新型的透气织物流场动量方程，将整个流场计算域分成伞衣厚度区域(多孔织物区)的流动和伞衣外的流动两部分，在伞衣织物区，将织物透气性模型引入动量方程的源项来考虑伞衣织物的透气性问题，数值结果较好的得到了伞衣的透流速度和绕透气伞衣的流场结构，和传统无透气性影响流场模型相比，数值结果更为准确。 1 环帆伞基本参数
本项目采用的环帆伞共有24个伞衣幅，单个伞衣幅结构如图 1所示，具体结构尺寸见表 1。
 |
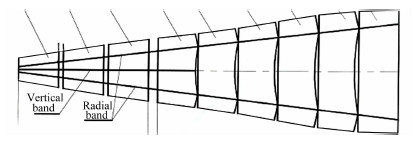| 图 1 环帆伞伞衣幅Fig. 1 A gore of the ringsail parachute |
|
Nominal diameter D0 | Gore height | Ring height | Gap width | Sail Height |
| 7.35 | 3.69 | 0.39 | 0.045 | 0.39 |
伞衣的环片和帆片为两种不同的材料，厚度分别为0.15mm和0.1mm。由于织物透气性对气动性能有重要的影响，本文计算时充分考虑了织物透气性的影响。各伞衣织物的透气性能可以采用Ergun公式描述[20]：
式中，a、b分别为描述织物透气性的粘性系数和惯性系数，e为伞衣厚度，vq为透过伞衣织物的气流速度，Δp为伞衣织物的试验压差。经过试验测量，分别得到两种织物材料的粘性系数a和惯性系数b：
环片：
α=1.3×106kg/(m3·s),b=6.47×105kg/m4
帆片：
α=1.89×106kg/(m3·s),b=1.17×106kg/m4 2 控制方程 2.1 流场控制方程
环帆伞稳降阶段速度小，为不可压流动，流场控制方程采用标准k-ε模型，其表达通式为：
式中，Φ、Γ分别为通用变量和扩散系数，s为源项。对于连续性方程、动量方程和源项，上面三项分别为：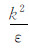
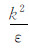)。本文算例中，对应系数取值为：c1=1.44,c2=1.92,cμ=0.09;湍动能k和耗散率ε的湍流普朗特数分别为：σk=1.0,σε=1.3。
2.2 织物透气性模型
空气透过伞衣微孔时，会存在压力降低，织物透气性能的好坏可用压力损失大小来描述。因此，本文考虑压力修正源项的方法来建立透气织物的新型流场动量方程，整个流场计算域分成多孔织物域(伞衣区)和自由域两部分，在多孔织物透气计算域，流场动量方程为：
式中，si为织物透气性引起的附加单位源项，其表达式如下： 式(4)中，等式右边分别为粘性损失项和惯性损失项。其中，α为渗透系数；C2为内部阻力因子21]。
当织物经纬向密度一致时，可认为多孔织物域透气性能为各项同性，据公式(1)织物透气性能的Ergun描述：Δp=(avq+bv2q)e。则沿i维方向的压力梯度为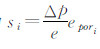
,式中epori为多孔介质计算i维方向的厚度(图 2)，则织物透气性能的三维源项表达为：
 |
| 图 2 流场织物透气域Fig. 2 Permeability of fabric region in the flow field |
降落伞在最后的稳定下降阶段，外形变化很小，可以假设该阶段形状不变，据表 1及空投图像资料数据处理后建立该降落伞的数值模型，伞衣存在一定厚度(图 2),为三棱柱体网格，伞衣表面为三角形(图 3)。流场计算域如图 4所示(其中D0为伞衣名义直径)，其伞衣中心区域的流场网格如图 5所示。
 |
| 图 3 降落伞模型Fig. 3 Parachute model |
 |
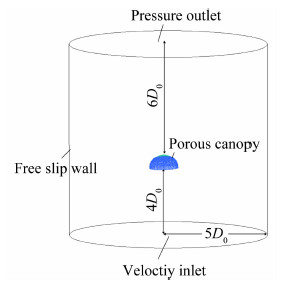| 图 4 流场计算域Fig. 4 Computational domain of the flow field |
 |
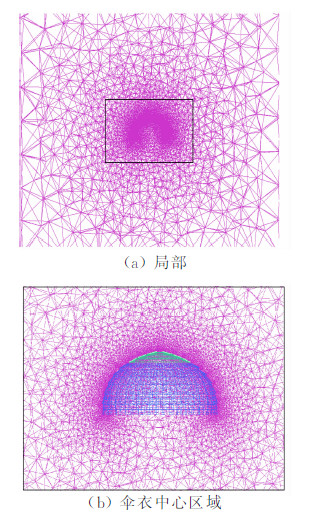| 图 5 伞衣对称面的网格Fig. 5 Grid in the symmetry plane of the canopy |
对透气模拟整个流场计算域分成多孔织物域(伞衣区)和自由域两大计算区域，其动量控制方程分别为式(2)和式(3)，非透气模拟则将伞衣设置为无滑移壁面边界条件，不添加动量方程源项。本文基于有限体积法对上述方程进行三维求解，为了加快计算速度，时间项采用了二阶格式的隐式双时间步离散求解方法[22]，空间对流项应用二阶迎风格式，粘性项则采用中心差分格式离散求解。
计算中定解条件如下设置：
初始条件：
v0i=vin=30m/s;p0=81000Pa;ρ0=1kg/m3
计算域边界条件：入口，v=vin；出口,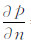
=0；四周壁面，vb=vin。
图 6~图 7分别为伞衣中心对称面流线图和压力云图，结果表明：伞衣尾部存在紧贴伞衣织物的第 一尾涡区和尾部中心旋涡对组成的第二尾涡区，织物透气性使第一尾涡区变长，螺旋点增多，旋涡分布更 均匀对称，而第二尾涡区尺寸则变小，整个尾涡区变短变窄，其宽度约缩小15％左右，长度减少25％左右。伞衣尾流压力分布更均匀，提高了伞衣的稳定性。
 |
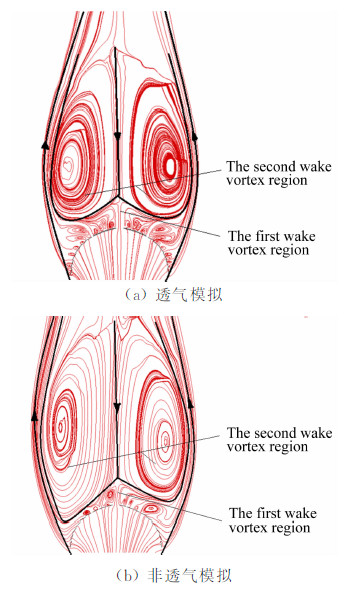| 图 6 伞衣对称面流线图Fig. 6 Streamline diagram in the symmetry plane of the canopy |
 |
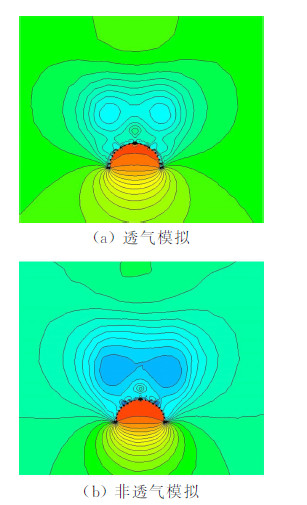| 图 7 伞衣对称面压力云图Fig. 7 Contours of pressure in the symmetry plane of the canopy |
图 8~图 9分别为伞衣环片局部压力云图和速度矢量图，结果表明：透气模拟的织物面处压力由内侧压力逐渐过渡到外侧压力，伞衣外侧压力分布较非透气模拟均匀，织物面处有明显的流体穿过，其流速低于周围有孔出流速度及自由来流速度，而非透气模拟气流均从结构透气孔处流出，表明本文采用的Ergun修正源项的动量方程模型可有效的模拟织物透气性情况。
 |
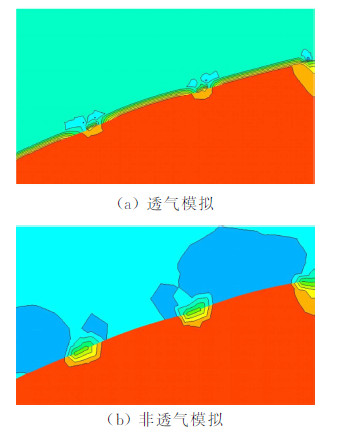| 图 8 伞衣环片局部压力云图Fig. 8 Contours of pressure around the ring |
 |
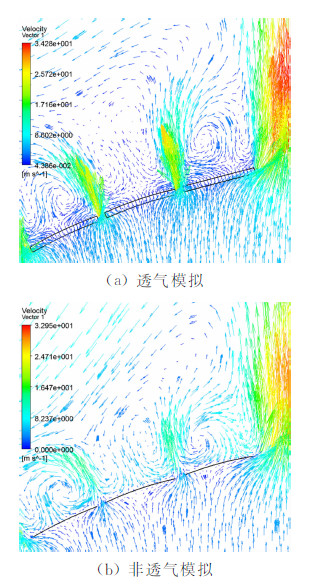| 图 9 伞衣环片局部速度矢量图Fig. 9 Velocity vector diagram around the ring |
本文对环帆伞稳降阶段进行了透气模拟和非透气模拟，其阻力系数分别为0.733和0.79，空投试验的平均阻力系数为0.731，两种模型阻力系数误差分别为0.27％和8％，可见本文建立的透气性流场模型使流场计算准确性大为提高。
图 10~图 11为伞衣沿子午线(无量纲量)上内外压力分布和压差系数，结果表明：透气性模型伞衣内侧压力低于或等于非透气模型，除第一环和第一帆外，外侧压力均大于非透气模型，可见透气性的存在使伞衣面存在透流速度(速度并不为0)，该速度导致伞衣内侧正压减小，伞衣外侧负压降低，造成透气性模型压差系数小于非透气性模型，该结果也与工程经验一致。
 |
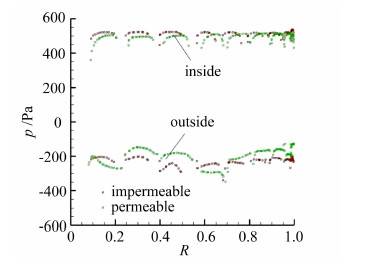| 图 10 伞衣沿子午线上内外压力分布Fig. 10 Internal and external pressure distribution along the meridian of the canopy |
 |
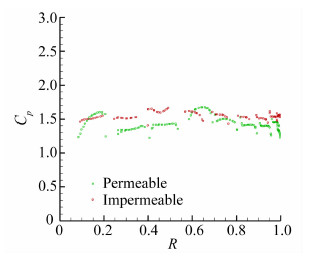| 图 11 伞衣沿子午线上压差系数Fig. 11 Pressure coefficient along the meridian of the canopy |
本文建立了微孔透气伞衣的流场方程，以某环缝伞为对象，开展了透气伞衣和非透气伞衣的绕流数值模拟，对数值结果进行了分析，得出如下结论：
(1) 采用对动量方程增加附加源项的新型流场控制方程能有效得到微孔伞衣的透流速度，计算结果更接近空投试验结果，准确性大为提高。
(2) 对伞衣尾部流场进行了分析，发现了两大尾涡区分布，透气性伞衣将使第一尾涡区变长，螺旋点增多，旋涡分布更均匀对称，而第二尾涡区变小，整个尾涡区变短变窄。
(3) 比较了透气性模型和非透气性模型的数值结果，透气性模型伞衣内侧压力略有降低，而外侧负压升高明显，伞衣阻力系数降低,尾流压力分布更均匀。
| [1] | Barber J, Johari H. Experimental investigation of personnel parachute designs using scale model wind tunnel testing[C]//16th AIAA Aerodynamic Decelerator Systems Technology Conference, Boston:MA, AIAA 2001-2074, 2001. |
| [2] | Yu Li, Ming Xiao, Cheng Liqun. Experimental investigation on the flow-field of different vent canopy[J]. Acta Aerodynamica Sinica, 2008, 26(1):19-24. (in Chinese)余莉, 明晓, 陈丽群. 不同透气情况降落伞的流场试验研究[J]. 空气动力学学报, 2008, 26(1):19-24. |
| [3] | Roberts B W. A contribution to parachute inflation dynamics[R]. AIAA-68-0928, 1968. |
| [4] | Meter J, Purvis T W. Vortex lattice theory applied to parachute canopy configurations[R]. AIAA-84-0787, 1984. |
| [5] | Parag K, Vijay G, Chaman S V. Numerical simulation of the flow past bluff bodies using discrete vortex methods[R]. AIAA-95-1559, 1995. |
| [6] | Shirayama S, Kuwahara K. Computation of flow past a parachute by a three-dimensional vortex method[C]//AIAA, 24th Aerospace Sciences Meeting, Reno, NV.1986. |
| [7] | Frucht Y, Cockrell D. A discrete free vortex method of analysis for inviscid axisymmetric flows around parachute canopies[R]. AIAA-91-0850, 1991. |
| [8] | Peng Yong, Song Xumin, Qin Zhizeng. Simulation of flow around a parachute shape by viscous vortex method[J]. Spacecraft Recovery & Remote Sensing, 2004, 25(4):10-14. (in Chinese)彭勇, 宋旭民, 秦子增. 用粘性涡方法计算伞状物绕流[J]. 航天返回与遥感, 2004, 25(4):10-14. |
| [9] | Stein K. Computations of the flow characteristics of aerodynamic decelerators using computational fluid dynamics[C]//Proceedings of AIAA 11th Aerodynamic Decelerator and Balloon Technology Conference, 1991:9-11. |
| [10] | Barnette D W. Preliminary numerical simulations for parachutes using a Navier-Stokes solver on a zoned grid[C]//AIAA Aerodynamic Decelerator Systems Technology Conference, 11th, San Diego, CA. 1991:323-332. |
| [11] | Li Xiaoyong, Cao Yihua, Jiang Congwen, et al. The numeric simulation of the parachute flow field during terminal descent[J]. Spacecraft Recovery & Remote Sensing, 2004, 25(2):5-9. (in Chinese)李晓勇, 曹义华, 蒋崇文, 等. 降落伞稳定下降阶段流场地的数值模拟[J]. 航天返回与遥感, 2004, 25(2):5-9. |
| [12] | Cao Yihua, Wan Kan, Song Qianfu, et al. Numerical simulation of parachute fluid-structure interaction in terminal descent[J]. Science China, 2012, 55(11):3131-3141. |
| [13] | Yu Li, Ming Xiao. Study on transient aerodynamic characteristics of parachute opening process[J].Acta Mechanica Sinica, 2007, 23(6):627-633. |
| [14] | Sahu J, Benney R. Prediction of terminal descent characteristics of parachute clusters using CFD[J]. AIAA-97-1453, 1997. |
| [15] | Tezduyar T E, Sathe S, Schwaab M, et al. Fluid-structure interaction modeling of ringsail parachutes[J]. Computational Mechanics, 2008, 43(1):133-142. |
| [16] | Han Y H, Wang Y W, Yang C X, et al. Numerical methods for analyzing the aerodynamic characteristics of cross parachute with permeability[C]//Proceeding of AIAA Aerodynamic Decelerator Systems (ADS) Conference, 25-28. |
| [17] | Aquelet N, Tutt B. Euler-Lagrange coupling for porous parachute canopy analysis[J]. The International Journal of Multiphysics, 2007, 1(1):53-68. |
| [18] | Tutt B, Charles R, Roland S. Development of parachute simulation techniques in LS-DYNA[C]//11th International LS-DYNA Users Conference, 2010. |
| [19] | Coquet Y, Bordenave P, Capmas G, et al. Improvements in fluid-structure interaction simulations of parachutes using LS-DYNA[C]//21st AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, 2011. |
| [20] | Han Cheng, Li Yu, Wei Rong, et al. A numerical study of parachute inflation bases on a mixed method[J]. Aviation, 2012, 16(4):115-123. |
| [21] | Ansys CFX-solver theory guide (Version 14.0)[R]. ANSYS, Inc, 2011. |
| [22] | Zhao Yunfei, Liu Xu, Tu Guohua, et al. High-accuracy numerical method applied to calculate unsteady Euler equations[J]. Journal of National University of Defense Technology, 2012, 34(3):12-16. (in Chinese)赵云飞, 刘绪, 涂国华, 等. 非定常Euler方程数值计算中高精度格式应用[J]. 国防科技大学学报, 2012, 34(3):12-16. |