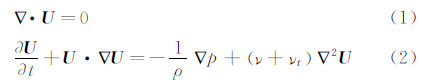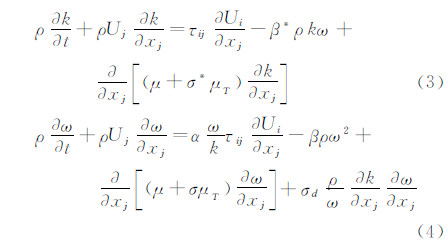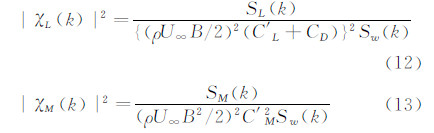0 引 言
气动导纳是描述自然风脉动速度到结构物所受气动力的传递函数,是桥梁风致抖振响应分析中的关键因素之一。气动导纳最初诞生于航空领域,20世纪30年代Von Karman[1]和Sears[2]在解析机翼抖振力时引入了气动导纳函数,基于势流理论推导得到薄翼气动导纳函数的理论解。随后Liepmann[3]将Sears函数进一步近似化简为更易使用的形式。气动导纳与物体形状及自然风湍流特性有关,早期的研究对象为薄翼或平板等流线体,这使得研究者能够从流体力学基本理论出发寻找气动导纳的解析解。对于复杂钝体绕流问题,由于存在流体理论描述的困难,只能通过试验手段获得其气动导纳。Davenport[4]给出了一定厚度矩形断面的气动导纳经验式。Holms[5]通过全桥气弹模型试验研究了West Gate桥的抖振响应,指出主梁断面气动导纳大于Sears函数,并通过间接修正Sears函数中的部分系数,使其可用于主梁断面的气动导纳描述。Walshe[6]基于Wye桥首次对桥梁断面气动导纳开展试验间接测量。此后Larose、Scanlan、Diana、Costa、马存明、王雄江等大量研究者[7, 8, 9, 10, 11, 12]对桥梁断面气动导纳进行了卓有成效的探索,发展出各种各样的识别方法,这些方法大致可归为两类,其一是同时测得脉动风谱与抖振力谱,再依二者比值直接拟合出气动导纳经验表达式;其二是不测试气动力,测试脉动风谱与气弹模型随机响应谱,再以系统辨识方法间接识别气动导纳,而这些研究均建立在风洞试验基础之上。
从试验研究所涉及的风场来看,识别气动导纳所用风场条件常见有两种。一为频率连续分布的局部各向同性紊流风场(宽带紊流),湍流能谱满足Kolmogorov“-5/3”定律,在该风场中识别气动导纳可一次性获得各个频率下气动导纳值,此类风场可由风洞中固定的被动湍流模拟装置(如尖劈、格栅、粗糙块)制造产生,但目标风场的低频和高频成分湍动能往往不易满足,使得一次识别全频率气动导纳在频率两端特别是高频段易导致较大误差。另一类为频率单一的谐波风场(窄带单频紊流),在该风场中识别气动导纳一般采用分离频率法,通过改变风场卓越频率进行多次识别,能独立保证高低频段各自的识别精度,该类风场只能在主动控制风洞(多风扇、主动叶栅)中获得,是当下研究的热点。需指出的是,由于湍流雷诺应力的能量再分配作用,初始时仅有单向速度脉动成分的一维湍流,会随着流动向下游的推移演化逐渐发展成具有三个方向速度脉动的三维湍流,实验室内生成的窄带单频紊流不可能保持严格意义上的单一频率,脉动频率必分布在一定频段范围内,在此风场中识别的气动导纳结果是有待商榷的。
风洞试验中要测试获得模型的气动力有两种途径,一是用天平直接连接模型测力,二是先测量表面压力再积分求合力。前者对模型制作要求十分苛刻,模型测力系统需具备足够高的频率(高于80Hz),模型在测试过程中不能发生变形和振动,否则将面临模型惯性力难剔除的困难。后者仅适用于闭口箱梁断面的气动导纳测试,无法考虑栏杆、轨道等桥梁附属设施的影响,且测试所得气动力还受测压孔布置方式及压力积分格式等多重因素影响严重,误差较大。
现场实测是研究真实桥梁气动导纳的最佳手段。陶奇[13]采用测压法现场实测研究苏通大桥主梁断面气动导纳,获取第一手珍贵实测数据,研究结果表明该桥现场实测气动导纳结果与风洞试验结果接近,与Sears函数有交叉。使用测压法的现场实测结果同样受测点布置和积分格式的影响,此外还要克服测压管路过长引起的各测点信号不同步及脉动信号失真的困难。就本文作者收集的文献资料来看,目前暂未见到其他有关桥梁断面气动导纳现场实测的公开报道。
正因为钝体扰流理论推导面临的障碍难以逾越,试验研究亦存在不少问题,现场实测研究凤毛麟角,近年来有少数学者开始尝试借助CFD数值模拟技术识别气动导纳。与风洞试验不同,数值识别中可直接生成完全单一频率的谐波风场,数值模型提取气动力简单便捷,研究周期短费用低,潜力巨大。Uejima[14]基于二维雷诺平均的CFD数值模拟生成单频谐波风场,研究平板、长宽比5∶1的矩形和扁平六边形断面的气动导纳,平板模拟结果与Sears函数十分接近,另外两个断面模拟结果也与试验吻合较好,但Uejima对计算来流特性的自保持问题讨论得不够,使得其识别的折算频率最大不超过0.7。韩艳[15]推导了6个复气动导纳定义式,并基于三维雷诺平均方法采用标准κ-ε模型研究平板的气动导纳,所得结果与试验值和Sears函数存在差别,其识别的折算频率最大不超过0.6。Rasmussen[16]基于二维离散涡方法生成频率连续的紊流风场,研究平板的气动导纳结果同Liepmann近似解较吻合,但在高频段(折算频率大于2)吻合度不太理想,其还研究大贝尔特东桥主梁的气动导纳,数值所得气动导纳同试验结果整体基本吻合,而高频段二者差异显著。总的来说,桥梁断面气动导纳的数值识别方法尚处于起步阶段,而基于雷诺平均CFD数值模拟识别桥梁断面气动导纳的研究则鲜有报道。
桥梁断面气动导纳数值识别的主要工作在于断面绕流场CFD计算,故须对流场计算中常见的几个问题予以足够关注。本文在Uejima[14]工作的基础上,首先对无障碍物计算域的入流自保持能力进行详细讨论,使其具备更广的折算频率识别范围,随后开展理想平板的气动导纳数值识别以验证方法,紧接着研究某桥梁断面的气动导纳并与风洞试验比较,最后还分析了流场初始化技术对数值计算效率的影响。与传统与风洞试验和现场实测相比,本文数值方法所生成的脉动风场具有单一频率,且在获取气动力的便捷性上亦有优势,为工程中识别桥梁断面气动导纳建议了一种新的途径。
1 数值模型 1.1 基本控制方程假设横向风绕过桥梁断面为二维不可压缩的流动过程,以非定常雷诺平均纳维-斯托克斯方程(URANS)为基本流动控制方程:
其中U为速度矢量,ν为空气分子粘度,νt为湍动粘度。选用SST κ-ω 湍流模型[17],其控制方程为:
模型封闭系数:
α=5/9,β=3/40,β*=9/100,σ=1/2,σ*=1/2
时间离散采用二阶隐式,对流项为二阶迎风格式,其它流动物理量的空间离散也为二阶格式,以SIMPLEC算法处理压强与速度耦合,数值求解在基于有限体积法的通用流体软件Fluent中完成。
1.2 计算域和边界条件模型计算域见图 1,在计算域左侧边界为速度入口条件,x方向速度保持恒定不变,y方向速度随时间简谐变化,通过用户自定义函数(UDF)编程实现。上下侧边界也为速度入口条件,y方向速度不仅随时间简谐变化,还随着空间位置不同而变化,以保持与左侧边界的波动特征相协调,其余边界参数设置与左侧边界类似。右侧边界为自由出流条件。桥梁断面为无滑移壁面条件。
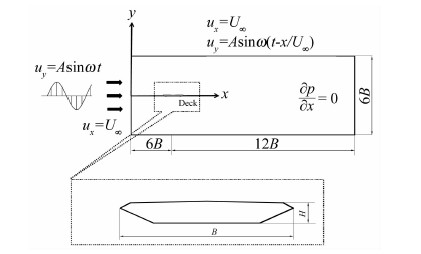 |
| 图 1 计算域Fig. 1 Computational domain |
数值模拟建模时未直接使用实际桥梁断面的原始尺寸,而采用风洞试验中常见的缩尺桥梁模型断面尺寸(梁宽B=0.5m~1m),并据此确定计算域大小,如图 1所示。该处理基于以下考虑:①气动导纳与桥梁断面形状有关,而受雷诺数影响较小[13];②现场实测极为少见,数值方法研究足尺断面气动导纳缺乏实测数据支持;③足尺建模的计算域太大,二维网格数量随计算域尺寸增大呈平方关系增长,计算量难以承受。
来流平均风速U∞取为12m/s, y向(竖向)速度简谐脉动幅值A取0.336,相应的湍流强度为2%。通常,来流的湍流强度会影响气动导纳的识别结果,但由于本文重点旨在介绍气动导纳的数值识别方法,对湍流强度的影响,未作详细讨论。
对无障碍物的计算域,按均匀方形结构化网格对其进行划分。对有桥梁断面的计算域网格划分如图 3,保持外围区域为均匀方形结构化网格不变,仅在断面附近区域内使用四边形非结构化网格,断面壁面网格局部加密以满足湍流模型对壁面网格y+值的要求,并通过尺寸函数控制渐变网格大小从壁面到均匀区域的平缓渐变,其相应的相邻网格尺寸增长因子为1.06。
2 入流自保持能力正确的数值方法必须和流动的物理性质一致。通常,在外部绕流的CFD数值模拟中,随时空变化的计算入流边界条件须具备在无障碍物的整个计算域中自然保持其边界特征的能力,应避免发生明显不符合计算者预期的幅值衰减(即数值耗散)和频率畸变(即数值弥散/色散),如雷诺平均(RANS)中大气边界层入流风剖面自保持[18, 19],又如大涡模拟(LES)中充分发展均匀湍流脉动特性自保持[20]。
在对桥梁断面气动导纳进行数值识别之前,同样需考察无障碍物计算模型入口处简谐速度分量的自保持能力,其中计算域网格分辨率和数值求解使用的非定常时间步长是关键影响参数。
2.1 网格分辨率的影响以往钝体绕流的数值模拟中有研究者[21]结合自身经验给出了钝体网格分辨率的经验值,且大多以壁面网格份数这种无量纲的形式表达。但他们重点关心研究对象的气动力或压强分布,其给出的网格分辨率建议值可能不适合本文时变来流脉动特征的自保持问题。在此从数值误差角度,对网格尺寸进行经验估计并验证。
一般认为数值误差主要产生于把连续的微分方程转换为各网格点处离散的代数方程的过程中,并随着对流扩散而存在于整个计算流场中,在时间步长和数值格式确定的情况下,离散误差的大小主要取决于网格尺寸。
附加在主流上的竖向简谐脉动速度对应的空间波长为:
式中U∞为计算来流平均风速,f为竖向脉动频率。要使该简谐波长能够在计算域内有效传播,则网格尺寸Δx应至少比波长小一个量级:
气动导纳通常表达为折算频率k的函数:
经整理,网格尺寸可按下式估计:
其中,B为待识别断面的宽度,N为单波长内网格数,需进一步研究确定。在无障碍物空计算域内试算,改变网格尺寸以考察y向简谐脉动速度在计算域内的自保持情况。待计算达到统计稳定后,顺主流方向沿直线y=0任意提取某时刻的脉动速度分量的空间分布,如图 2所示。图中相邻两波峰间幅值衰减可用对数衰减率δ表示:
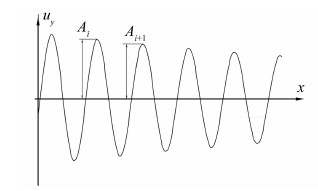 |
| 图 2 竖向脉动衰减示意Fig. 2 Decay of the vertical velocity |
本文在此处约定,当δ≤0.003时,认为数值耗散可接受,来流脉动特征实现自保持。
兼顾计算效率的同时,应尽可能地减小时间离散带来的误差。试算时采用的时间步长为0.0001s,采样频率10000Hz,而通常气动导纳研究考查的最 大折算频率约为10,若按断面宽度0.6m计,对应的简谐速度脉动频率为31Hz,采样频率约为最大简谐速度脉动频率的300倍,时间离散误差的影响可忽略。
在不同折算频率下进行数值试算,考查网格尺寸对来流脉动速度分量在计算域内自保持能力的影响,结果见图 3。竖向简谐脉动速度的衰减受网格尺寸影响显著,随着网格数量的倍增,脉动速度幅值的对数衰减率与之成平方关系减小,且两个折算频率下的衰减规律是一致的。
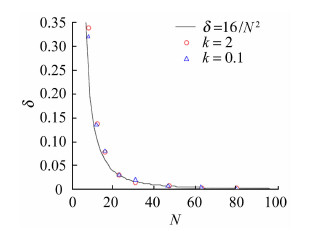 |
| 图 3 单波网格数对竖向脉动速度衰减的影响Fig. 3 Decay of vertical velocity influenced by N |
通过数据拟合,可得对数衰减率经验表达式:
图 3中按该式绘制的曲线与两个折算频率下的试算结果均吻合良好,说明用该经验式近似描述流场竖向简谐速度脉动衰减规律是可行的。
当单波网格数N达80时,对数衰减率不超过0.003。在进行气动导纳数值识别的流场网格划分时,建议按式(8)确定计算域最大网格尺寸,且式中单波网格数N应不小于80,可基本保证来流脉动速度的自保持。
2.2 时间步长的影响取单波网格数N为80,考查时间步长对简谐脉动速度幅值的影响。基于来流速度和计算域网格尺寸,定义一个无量纲时间步长
表 1所示试算结果反映时间步长对简谐脉动速度幅值的影响。时间步长越小,脉动速度的衰减也越小,当无量纲时间步长小至1.2时,计算来流脉动速度幅值的对数衰减率可控制在0.003以下,高、低折算频率条件下试算得到的衰减规律基本一致。在进行气动导纳识别时,建议无量纲时间步长取值应不大于1.2,据此估算相应计算工况的时间步长。另外,本研究试算中还观察到网格分辨率和时间步长对脉动速度频率无明显影响,不再赘述。
| 算例 | 折算频率 k/Hz | 网格尺寸 Δx/m | 时间步长 dt/s | 无量纲时间 步长dt′ | 对数衰减率 δ/10-3 |
| 1 | 2 | 0.005 | 0.0005 | 1.2 | 2.35 |
| 2 | 2 | 0.005 | 0.001 | 2.4 | 11.5 |
| 3 | 2 | 0.005 | 0.002 | 4.8 | 78.7 |
| 4 | 2 | 0.005 | 0.004 | 9.6 | 499 |
| 5 | 0.1 | 0.1 | 0.01 | 1.2 | 0.5 |
| 6 | 0.1 | 0.1 | 0.02 | 2.4 | 16 |
| 7 | 0.1 | 0.1 | 0.04 | 4.8 | 104 |
| 8 | 0.1 | 0.1 | 0.08 | 9.6 | 742 |
在数值识别气动导纳时,断面升力的功率谱表示为:
其中,k为式(7)定义的折算频率,|χL(k)|2为升力的气动导纳,|χM(k)|2为力矩的气动导纳,SL(fr)为升力频谱,SM(fr)为力矩频谱,CD、CL、CM分别为阻力、升力和力矩系数,C′L、C′M分别为升力系数和力矩系数对风迎角的斜率,ρ为空气密度,U∞为来流平均风速,B为断面宽度。升力气动导纳的识别过程如下:①在均匀流条件下,通过CFD计算获得C′L+CD值;②生成具有单一折算频率简谐脉动分速度的风场,计算获得该风场中待研究断面的升力时程;③对升力时程进行快速傅里叶变换获得频谱数据,代入式(11)计算该折算频率下的气动导纳值;④改变折算频率,重复步骤②③,直至在所考察折算频率范围内获得足够多的数据点,以拟合气动导纳函数。同理可识别力矩的气动导纳。
因本文重在介绍气动导纳的数值识别方法,故未对气动导纳理论如三维气动导纳[11]或六分量导纳[15]等做深入研究。
3.1 平板气动导纳对于理想平板升力气动导纳的Sear函数,Liepmann给出的理论近似解为:
数值计算中取宽厚比为100的矩形平板进行建模,为减小钝角引起的流动分离,对平板前后缘倒大圆角处理。对于平板,其阻力系数为零,升力系数斜率为2π。图 4为平板升力气动导纳的识别结果,并与近似解析解相比较。不难看出,无论是在高折算频率还是在低折算频率,平板气动导纳的数值识别结果与按势流理论推导得到的Sears函数都吻合得非常好。
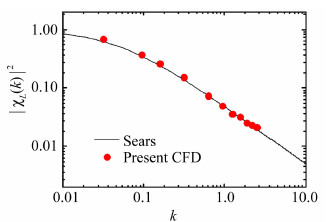 |
| 图 4 平板的气动导纳Fig. 4 Aerodynamic admittance of thin plate |
南京三桥(NJ3B)主梁为一典型扁平钢箱梁,宽高比11.6,本文作者之一曾对该桥主梁断面气动导纳进行了详细的风洞模型试验测试[11],试验模型断面如图 5所示。在此以该断面为例,验证数值方法对桥梁断面气动导纳的识别能力。
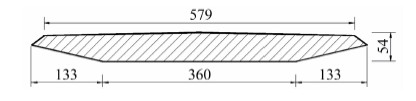 |
| 图 5 南京三桥主梁模型断面(mm)Fig. 5 Section of NJ3B(unit:mm) |
在均匀来流条件下,先识别模型断面的三分力系数,结果见图 6,其中力矩方向以图 1中顺时针为正。零度迎角来流时,计算得到的升力系数斜率为5.294,与文献[11]中的试验值5.302十分吻合;力矩系数斜率为1.532,与试验值1.305比较接近;计算的阻力系数为0.213。这些数据作为基本参数,代入式(11)、式(12)用于断面气动导纳的识别。
 |
| 图 6 南京三桥主梁静力三分力系数Fig. 6 Static coefficients of NJ3B |
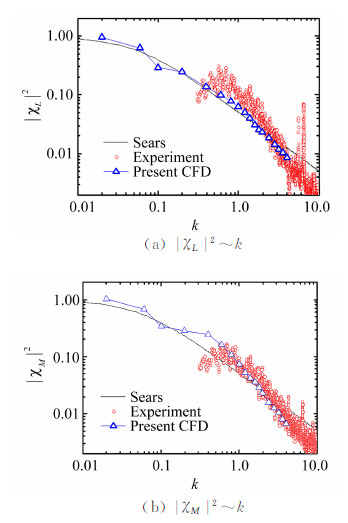
南京三桥主梁断面的气动导纳识别结果见图 7,其中用于结果比较的试验测试风场为固定格栅制造的紊流,竖向积分尺度为0.41m。
 |
| 图 7 南京三桥断面的气动导纳Fig. 7 Aerodynamic admittance of NJ3B |
就升力气动导纳而言,扁平箱梁断面的数值识别结果与Sears函数相比,在低频范围内非常接近,在高折算频率段略低,但与已有试验结果在折算频率(0.3,4)范围内亦吻合良好。
就力矩气动导纳而言,扁平箱梁断面的数值识别结果与Sears函数存在明显差异。原因应在于:Sears函数描述的对象为0°风迎角下的类平板薄翼,当迎角小范围变化时,其气动中心是基本固定的,而对于截面形式非对称的扁平箱梁断面,并不具备固定的气动中心,造成了二者在结果比较上的困难。但数值识别的结果与已有试验在高折算频率段却有着很好的吻合度。
对于更高的折算频率范围(k>4),未做更进一步的计算验证主要基于如下两个原因:①本文识别气动导纳折算频率范围(0.01,4)已能满足常规抖振计算需要。桥梁断面气动导纳识别主要用于大跨度桥梁抖振计算,以桥面宽30m为例,一般大跨度桥梁常见的设计风速值约为35m/s,主梁一阶竖弯频率约为0.2~0.4Hz,则其对风致振动敏感的折算频率在0.17~0.34附近,本文所识别气动导纳的折算频率范围已将其包含在内。②计算资源的限制。以本文识别的最高折算频率k=4为例,为保证来流的自维持,二维模型的网格数量需达400万,若要识别k=10时的气动导纳值,单向网格尺寸需细化至该模型的2/5,由于数值模型的两个维度,则计算模型网格总数将达2500万,普通工程计算难以承受。
3.3 流场初始化条件的讨论在数值模型建立后,需预先人为给定流场初始值作为迭代计算的初始化条件。合理的初始化流场能帮助数值计算过程顺利收敛,提高计算效率,故流场的初始化条件是值得研究的。
对钝体空气绕流问题,大多数研究者习惯参考来流边界条件的参数对所有流场内点进行赋值,所得初始流场物理量处处相等,为均匀常数场。当入口边界为定常条件时,这样的常数初始场是非常合理的,而当入口边界为非定常时,由于入口的时变信息传播至模型处需要一定的计算时间,常数初始场不一定为最优,这时可考虑非均匀的初始化条件。
通过Fluent软件预留的用户自定义函数(UDF)接口自编程序,以计算域上下边界处(图 1)的波动方程对全场速度进行流场初始化。湍动能和比耗散率仍参考入流边界取常数值均匀初始化。
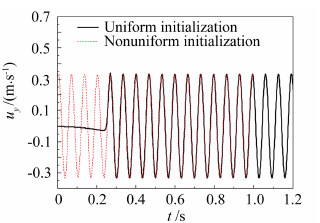
对来流自保持问题中无障碍物计算域进行数值模拟,监视计算域(6B,0)点处y向速度时程,对比两种初始化条件对计算过程的影响,如图 8所示。当采用均匀条件初始化流场时,计算初级监视点处y向速度基本为零,经过一段时间后开始进入等幅简谐脉动。可对该时间长度进行估算:由边界时变信息的传播速度为U∞/f,入口边界到计算关心区域的距离为6B,则传播用时6Bf/U∞。这段计算时间对于气动导纳的识别没有实际意义,仅是流场初始条件不够好所造成的额外迭代过程耗费。当采用恰当的非均匀初始化条件,可快速获得流场稳态振荡解。
 |
| 图 8 监视点的速度分量时程Fig. 8 Time history of the vertical velocity for monitored point |
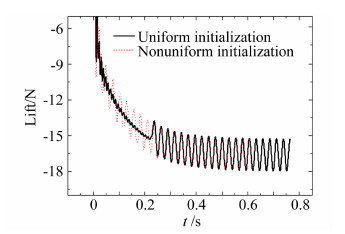
图 9所示为k=2时两种初始条件下的南京三桥断面升力曲线。从图中曲线来看,随着计算时间的推移,两种初始条件下计算的断面升力最终都将进入周期振荡,初始条件的影响主要表现在数值迭代开始时解的振荡差异上。气动导纳识别所用升力时程须选取稳定振荡部分的数据,从这个意义上看,两种初始化条件并无明显的效率差别。造成该现象的原因在于:非均匀初始化技术主要是节约来流边界时变信息传播到数值计算关心区域的时间t1,而对由桥梁断面附近因断面存在所造成的有物理意义的流场收敛尚需时间t2演化,当t1不显著大于t2时,流场非均匀初始化的优势并不十分明显。由此还可推断,当待识别断面距离入口边界较远或来流速度很小时,使用非均匀初始化条件将在一定程度上提高识别效率。
 |
| 图 9 断面升力时程Fig. 9 Lift history of NJ4B deck |
本文考查一种基于二维URANS的桥梁断面气动导纳数值识别方法,得到如下结论:
(1) 来流的竖向简谐脉动速度在计算域内的自保持能力受网格分辨率和时间步长的影响,单波长内的网格数越大,对应的无量纲时间步长越小,该简谐脉动速度幅值衰减程度越小。
(2) 提出了竖向简谐脉动速度幅值衰减效应的估算公式,据此确定数值模型最大网格尺寸与时间步长,可保证来流脉动速度幅值不发生明显衰减,这也是气动导纳识别的前提条件。
(3) 平板升力气动导纳的数值识别结果与Sears解析解高度吻合,证明了数值方法的正确性和可行性。桥梁断面升力气动导纳数值识别结果在低频段与Sears解吻合较好,在高频段虽低于Sears解,但与既有文献中的风洞试验结果基本一致,为本文数值方法的工程应用建立了信心。
(4) 流场初始条件对计算效率确有影响。总体上看,数值识别时使用恰当的非均匀初始条件要比使用均匀初始条件有利于提高效率。
建议进一步开展顺风向简谐脉动速度自保持能力研究,以及桥梁、高层建筑等结构断面阻力气动导纳的数值识别工作。
| [1] | Karman T H V, Sears W R. Airfoil theory for non-uniform motion[J]. Journal of the Aeronautical Sciences, 1938, 5(10):379-390. |
| [2] | Sears W R. Some aspects of non-stationary airfoil theory and its practical application[J]. Journal of the Aeronautical Sciences, 1941, 8(3):104-108. |
| [3] | Liepmann H W. On the application of statistical concepts to the buffeting problem[J]. Journal of the Aeronautical Science, 1952, 19(2):793-800. |
| [4] | Davenport A G. Buffeting of a suspension bridge by storm winds[J]. Journal of Structural Engineering, 1962, 88(ST3):233-268. |
| [5] | Holmes J D. Prediction of the response of a cable-stayed bridge to turbulence[C]. Proceedings of the Fourth International Conference on Wind Effects on Buildings and Structures, Heathrow, 1975, 187-197. |
| [6] | Walshe D E, Wyatt T A. Measurement and application of the aerodynamic admittance function for a box-girder bridge[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1983, 14(1):211-222. doi:10.1016/0167-6105(83)90024-7 |
| [7] | Larose G L, Mann J. Gust loading on streamlined bridge decks[J]. Journal of Fluids and Structures, 1998, 12(5):511-536. doi:10.1006/jfls.1998.0161 |
| [8] | Scanlan R H, Jones N P. A form of aerodynamic admittance for use in bridge aeroelastic analysis[J]. Journal of Fluids and Structures, 1999, 13(7):1017-1027. doi:10.1006/jfls.1999.0243 |
| [9] | Diana G, Bruni S, Cigada A, et al. Complex aerodynamic admittance function role in buffeting response of a bridge deck[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(12):2057-2072. doi:10.1016/S0167-6105(02)00321-5 |
| [10] | Costa c. Aerodynamic admittance functions and buffeting forces for bridges via indicial functions[J]. Journal of Fluids and Structures, 2007, 23(3):413-428. doi:10.1016/j. jfluidstructs.2006.10.002 |
| [11] | Ma Cunming. 3D aerodynamic admittance research of streamlined box bridge decks[D].[PhD Thesis]. Chengdu:Southwest Jiaotong University, 2007. (in Chinese)马存明. 流线箱型桥梁断面三维气动导纳研究[D].[博士学位论文]. 成都:西南交通大学, 2007. |
| [12] | Wang Xiongjiang, Gu Ming, Qin Xianrong. Estimation of aerodynamic admittance function of long-span bridges by the relationships among aerodynamic parameters[J]. Acta Aerodynamica Sinica, 2009, 27(6):707-712. (in Chinese)王雄江, 顾明, 秦仙蓉. 基于气动参数之间关系的桥梁断面气动导纳识别[J]. 空气动力学学报, 2009, 27(6):707-712. |
| [13] | Tao Qi, Liao Haili, Li Mingshui, et al. The actually test research of aerodynamic admittance of long-span cable-stayed bridge girder section[J]. Acta Aerodynamica Sinica, 2010, 28(006):655-660. (in Chinese)陶奇, 廖海黎, 李明水, 等. 大跨斜拉桥主梁断面气动导纳的实测研究[J]. 空气动力学学报, 2010, 28(006):655-660. |
| [14] | Uejima H, Kuroda S, Kobayashi H. Estimation of aerodynamic admittance by numerical computation[C]. BBAA Ⅵ International Colloquium on Bluff Bodies Aerodynamics and Applications, Milano, Italy, July, 20-242008 |
| [15] | [KG0.5mm] Han Yan, Chen Zhengqing. Experimental and numerical simulations studies on complex aerodynamic admittance functions of thin plate section[J]. Journal of Vibration Engineering, 2009, 22(2):200-206. (in Chinese)韩艳, 陈政清. 薄平板复气动导纳函数的试验与数值模拟研究[J]. 振动工程学报, 2009, 22(2):200-206. |
| [16] | Rasmussen J T, Hejlesen M M, Larsen A, et al. Discrete vortex method simulations of the aerodynamic admittance in bridge aerodynamics[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2010, 98(12):754-766. doi:10.1016/j.jweia.2010.06.011 |
| [17] | Menter F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8):1598-1605. doi:10.2514/3.12149 |
| [18] | Richards P J, Younis B A. Comments on "Prediction of wind-generated pressure distribution around buildings" by E. H. Mathews[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1990, 34(1):107-110. doi:10.1016/0167-6105(90)90152-3 |
| [19] | Yang Y, Gu M, chen S, et al. New inflow boundary conditions for modelling the neutral equilibrium atmospheric boundary layer in computational wind engineering[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2009, 97(2):88-95. doi:10.1016/j.jweia.2008.12.001 |
| [20] | Tamura T, Ono Y. LES analysis on aeroelastic instability of prisms in turbulent flow[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91(12):1827-1846. doi:10.1016/j.jweia.2003.09.032 |
| [21] | Kravchenko A G, Moin P. Numerical studies of flow over a circular cylinder at Re=3900[J]. Physics of Fluids, 2000, 12(2):403-417. doi:10.1063/1.870318 |