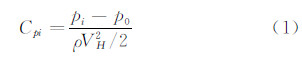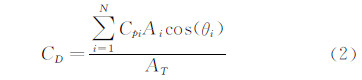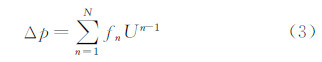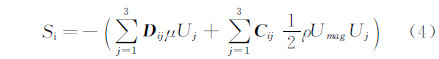2. 高速铁路建造技术国家工程实验室, 湖南 长沙 410075;
3. 湖南大学 风工程试验研究中心, 湖南 长沙 410082
2. National Engineering Laboratory for High Speed Railway Construction, Changsha 410075, China;
3. Wind Engineering Research Center, Hunan University, Changsha 410082, China
0 引 言
为实现循环水的冷却,冷却塔风筒顶部敞开,底部由人字柱支撑而形成风通道,故其内表面也受到风荷载作用。相对外表面风荷载而言,有关冷却塔内表面风荷载的研究成果较少,我国规范也未对其取值作出相关规定,但明确指出在进行塔筒局部弹性稳定性验算时必须要考虑内压产生的应力[1, 2]。研究表明[3],考虑内压效应后,环向压应力增大,结构的整体稳定性与局部弹性稳定性降低,这 一趋势可能随着冷却塔高度的增加而更加显著。随着我国电力事业的发展,我国冷却塔高度即将突破现有世界纪录(200m),此类超 大型冷却塔设计的风荷载取值既无规范指导,又无实际工程经验借鉴,因此亟需开展相关研究。
孙天风通过对茂名冷却塔的实测研究发现强风作用下的内压并非沿环向均匀分布[4];Kasperski通过风洞试验发现内压沿环向和高度均匀分布,压力系数值接近-0.50[5];李鹏飞的风洞试验结果表明内压基本均匀分布,但大小与与填料层透风率密切相关[6];张陈胜[7]、沈国辉[8]等通过CFD方法对内压分布进行了研究,结果表明内压沿高度和环向变化明显;鲍侃袁通过CFD数值模拟发现塔底尾流区内侧风压急剧减少[9];余关鹏[10]、沈国辉[11]等通过风洞试验发现内压在底部180°圆周角急剧减少。此外,一些学者认为内压沿环向、高度不变,根据经验假定它为某一数值,例如,Diver[12]认为内压压力系数取值在 -0.40~-0.50之间,Sollenberger[13]认为取值为-0.40,Scanlan[14]在由内外压差实测数据获得外表面风压系数时取内压为-0.40,Kawarabata[15]认为实际设计中内压可取为-0.45。由以上成果可以看出,虽然一些学者认为内压沿环向、高度不变,但不同学者的取值略有差异,也有研究结果(包括实测、数值模拟和风洞试验)表明内压沿高度变化,沿环向分布也并不均匀,可见人们对冷却塔内表面风荷载分布尚无统一认识。此外,从上述综述可以看出,人们通常采用单一手段对内压进行研究(风洞试验或数值模拟),但由于冷却塔壁厚较薄,风洞试验中内压刚性模型几何缩尺比较小,通常只能保证内表面几何相似而不满足外表面相似,且无法模拟冷却塔运行过程中由塔内、外空气压差产生的向上抽力等,这些因素可能会对内压试验结果产生影响;而数值模拟方法尽管可以较好地解决上述不足,但其计算结果的可靠性也需要风洞试验结果的验证。
本文以某拟建的220m高双曲冷却塔为例,通过刚性模型测压风洞试验对其内表面风荷载进行研究,考虑试验风速、十字挡风板、填料层透风率等参数对内压的影响,并通过CFD数值模拟分析风洞试验存在的不足及其对试验结果的影响,将两种方法得到的结果进行对比,以对结果的可靠性进行相互验证。
1 风洞试验概况 1.1 试验模型与测点布置某内陆拟建冷却塔淋水面积为20000m2,塔顶 标高220.0m,喉部标高169.4m,进风口标高13.45m,人字柱底面标高0m,塔顶直径109.0m,喉部直径103.5m,底部直径169.9m,风筒采用分段等厚,最小厚度在喉部断面,壁厚0.23m,最大厚度在下环梁位置,壁厚1.4m,由均匀分布的56对Φ1.4m人字柱支撑。刚性模型测压风洞试验在湖南大学HD-2风洞的高速试验段进行,试验段长17.0m,宽3.0m,高2.5m。试验模型采用6mm厚的有机玻璃制作,保证模型具有足够的强度和刚度,在试验风速下不发生变形及不出现明显的振动。模型几何缩尺比为1∶220,内表面在外形上与实际结构保持几何相似,外表面几何相似则由于结构壁厚太薄而无法满足,模型底部由严格几何缩尺的人字柱支撑,保证人字柱之间的空隙使得空气可以自由出入,确保真实模拟冷却塔内部空气流动特征。试验模型照片如图 1所示。在模型内表面共布置14层测点,每层沿环向等间距布置36个测点,共计504个内压测点,测点布置如图 2所示。
 |
| 图 1 试验模型Fig. 1 Test model |
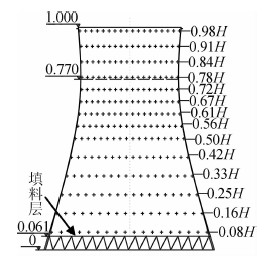 |
| 图 2 测点布置Fig. 2 Pressure port arrangement |
试验对多种不同透风率填料层下的内压分布进行了测试,以比较填料层透风率对内压的影响,其中填料层模型开孔均匀布置以尽可能的模拟实际填料层通风情况(图 3(a))。考虑到不同试验风速下塔内空气流量不一致可能会影响内压分布[16],因此每个工况进行了多个试验风速的测试。还研究了底部有无十字挡板对内压的影响(图 3(b))。当塔底有十字挡板时,结构为非轴对称结构,因此进行了多个风向角的测试(风向角定义如图 3(c)所示)。详细试验工况安排如表 1所示,共进行了约300个吹风工况。
 |
| 图 3 填料层与十字挡风板模型及风向角定义Fig. 3 Model and define of wind direction |
| 工况编号 | 填料层透风率/% | 十字挡板 | 风场类型 | 风向角β/(°) | 试验风速υ/(m·s-1) |
| 1 | 100 | 有、均匀流场、 无B类风场 |
0、20、45 | 6、8、 10、12、14 |
|
| 2 | 85 | ||||
| 3 | 80 | ||||
| 4 | 70 | ||||
| 5 | 55 | ||||
| 6 | 30 | ||||
| 7 | 15 | ||||
| 8 | 10 | ||||
| 9 | 5 | ||||
| 10 | 3 | ||||
| 11 | 0 | ||||
项目厂址周边地形与GB 50009—2001《建筑结构荷载规范》规定的B类地貌类似,在湖南大学HD-2风洞高速试验段模拟了B类地貌风场,转盘中心处的模拟结果如图 4所示,其中u350代表梯度风风速。从图 4(a)可以看出,风洞中模拟的平均风速剖面与 GB 50009—2001《建筑结构荷载规范》规定的B类风场基本一致,湍流度剖面也与实际大气中的情况基本一致。图 4(b)给出了转盘中心50cm高处的顺风向脉动风谱,可以看出,模拟的顺风 向脉动风谱与常用的von Karman、Kaimal、Davenport等理论谱基本一致。
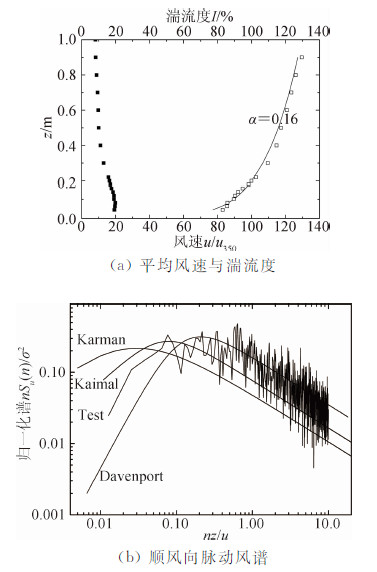 |
| 图 4 风洞中大气边界层的模拟Fig. 4 Simulation of wind characteristics in Boundary Layer Wind Tunnel |
任意测点i处的风压系数Cpi表示为:
式中,pi为测点i处的压力;ρ为空气密度,取ρ=1.225kg/m3;p0为来流静压;vH为塔顶高度处来流风速。对于冷却塔这种圆形截面结构,截面顺风向阻力系数CD可由风压系数积分得到。设某截面布置N个风压测点,其计算表达式如下:
式中,Ai为第i个测点代表的面积,θi为第i测点法向与来流方向夹角,AT为结构沿顺风向的投影面积。 2 风洞试验结果与分析 2.1 试验风速对内压的影响以透风率100%、塔底无十字挡板、B类风场、各试验风速下的试验结果分析来流大小对内压的影响。之所以选择透风率100%作为比较工况,这是因为大多研究结果考虑的透风率均为100%,便于与已有研究成果比较,且该透风率在施工过程中也普遍存在,另经比较发现各参数对不同透风率工况影响规律也基本一致。不同试验风速下冷却塔上部、中部、下部三段区域内典型高度的内表面风压沿环向分布情况如图 5所示。从图 5中可以发现,内表面风压系数沿环向分布趋势 基本不受试验风速影响,且除v=6m/s时的测试结果略有偏 差外,其它试验风速下的风压系数大小也基本一致。图 6所示为各试验风速下截面阻力系数CD sec结果,各曲线的重合进一步说明了试验风速对内压沿环向的分布特征基本没有影响。图 7给出的是不同风速下各层测点风压系数的平均值沿高度变化曲线。由图 7可以看出,除v=6m/s时由于风速太小测试结果略有偏差外,其它试验风速下各高度的风压系数特征值基本一致,平均风压系数在-0.50~-0.60范围内变化。
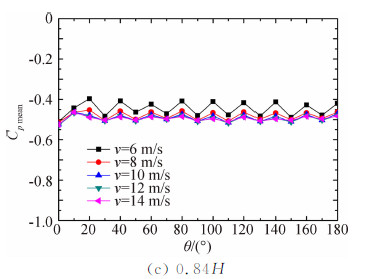 |
| 图 5 不同试验风速下典型高度平均风压系数比较Fig. 5 Cp mean of typical height for different test speed |
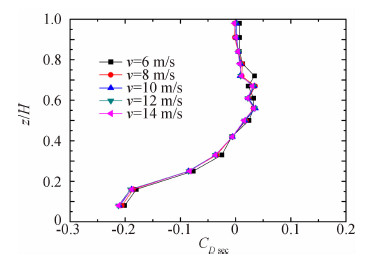 |
| 图 6 截面阻力系数比较Fig. 6 Comparison of CD sec |
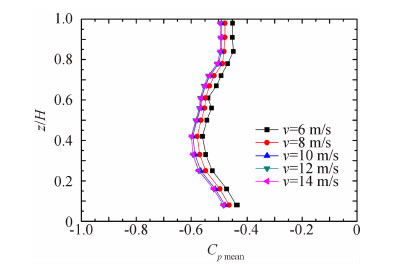 |
| 图 7 平均风压系数沿高度变化Fig. 7 Variation of Cp mean along height |
图 8给出的是透风率100%时、在B类风场中、塔底有/无十字挡风板时典型高度内表面平均风压系数沿环向分布情况,有十字挡板时考虑了风向角对塔内风压的影响。由图 8可知,增加十字挡风板后,塔底内压沿环向分布更为均匀,没有在180°圆周角附近发生突变;中段内压则在180°圆周角附近有增大的趋势,这是因为塔底设置十字挡风板后,撞击在尾流区内壁的气流上移;上部内压沿环向的分布趋势受十字挡风板影响不大;有十字挡风板时,不同风向角下的内压分布特征基本一致,表明风向角对内压影响较小;塔底增加十字挡风板后,各高度的风压系数绝对值略小于无十字挡板时。
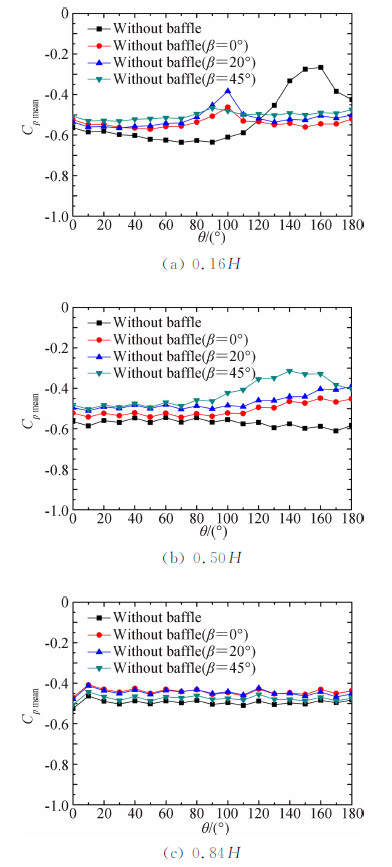 |
| 图 8 不同风向角下典型高度平均风压系数比较Fig. 8 Cp mean of typical height for different yaw angle |
各工况的截面阻力系数比较如图 9所示。由图 9可以更加清楚地看到十字挡风板及风向角对内压沿环向分布特征的影响:有十字挡风板时,底部截面阻力系数绝对值比没有十字挡风板时小,表明增加十字挡板后塔底内压沿环向分布更为均匀;而对于0.30H~0.50H截面,增加十字挡风板后的阻力系数绝对值大于无十字挡板,说明该高度范围内压沿环向分布的均匀性在塔底无十字挡板时较好;塔顶各高度截面阻力系数在有、无十字挡风板时基本一致,说明十字挡板对塔顶各高度的内压沿环向分布特征影响较小;有十字挡风板时,不同风向角下截面阻力系数曲线的重合说明风向角对塔内风压沿环向的分布特征基本没有影响。
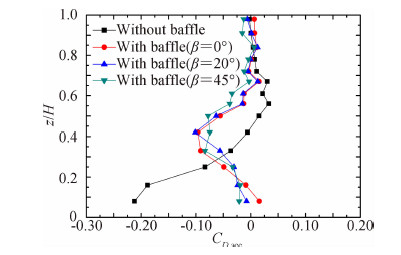 |
| 图 9 截面阻力系数比较Fig. 9 Comparisonof CD sec |
图 10给出的是不同工况下各层测点风压系数的平均值沿高度变化曲线。由图 10可以看出,增加十字挡板后,内压均值波动性减小,沿高度基本不变,且绝对值略有减小;有十字挡板时,各风向角下的风压系数特征值沿高度变化趋势基本一致且大小相当,平均风压系数约为-0.50。
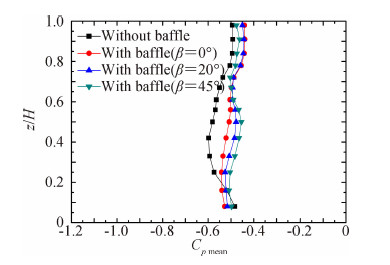 |
| 图 10 平均风压系数沿高度变化Fig. 10 Variation of Cp mean along height |
B类风场不同透风率下典型高度的内压均值沿环向分布情况如图 11所示。由图 11可知,各透风率下的内压沿环向分布趋势基本一致,均沿环向基本不变;内压绝对值以透风率为0%时最大,并随透风率的增大略有减小,但当透风率大于10%后变化较小。为更清晰地比较透风率对内压沿环向分布特征的影响,将各工况的截面阻力系数结果列于图 12。可以看出,透风率小于70%时,截面阻力基本接近0,表明内压沿环向基本均匀分布;但当透风率大于70%后,0.30H~0.50H范围内的阻力系数偏离0较远,表明该范围内的风压沿环向分布略有不均匀,受侧风影响明显。图 13给出的是不同透风率下各层测点风压系数的平均值沿高度变化曲线。由图 13可以看出,各透风率下的风压系数特征值均值沿高度变化趋势基本一致,均沿高度基本不变;平均风压系数绝对值随透风率的增大而减小,但当透风率大于10%后各 风压系数特征值基本不随透风率变化,各高度平均风压系数约为-0.50。
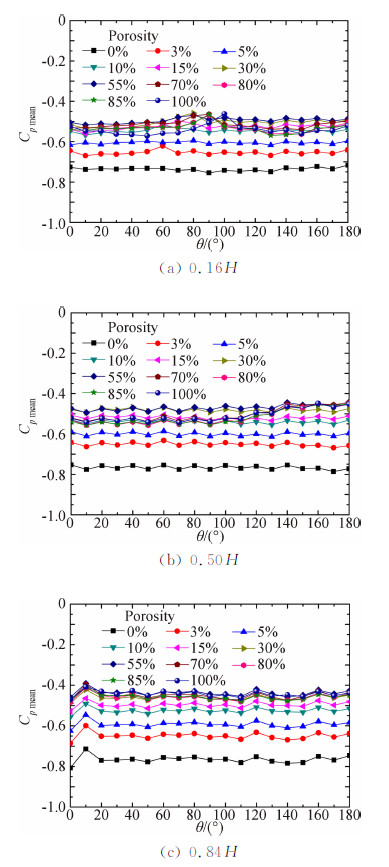 |
| 图 11 不同透风率典型高度平均风压系数比较Fig. 11 Cp mean of typical height for different porosity |
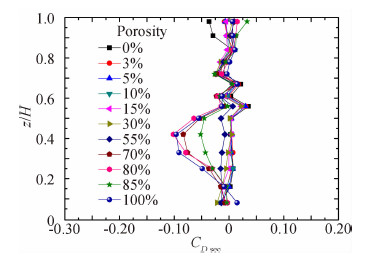 |
| 图 12 截面阻力系数比较Fig. 12 Comparison of CD sec |
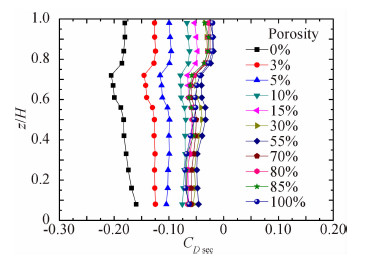 |
| 图 13 平均风压系数沿高度变化Fig. 13 Variation of Cp mean along height |
由以上参数分析结果可知,内表面风压系数沿环向、高度基本不变,因此取所有测点风压系数特征值的算术平均作为该工况测试结果的代表值。图 14所示为各风压系数代表值随透风率的变化曲线。可以看出,两类流场中各代表值的绝对值均在透风率为0%时达到最大,并都随透风率的增大略微减小,但当透风率大于10%后,各风压系数代表值基本不再随透风率变化;透风率小于10%时,均匀流场中的平均风压系数绝对值与B类风场相当,但透风率大于10%后,均匀流场要比B类风场约大20%;而脉动风压刚好相反,透风率小于10%时,均匀流场中的脉动风压系数显著小于B类风场,透风率大于10%后,均匀流场的脉动风压系数与B类风场相当;B类风场中,平均风压系数约为-0.50,脉动风压系数约为0.045;均匀流场中,平均风压系数约为-0.61,脉动风压系数约为0.035。
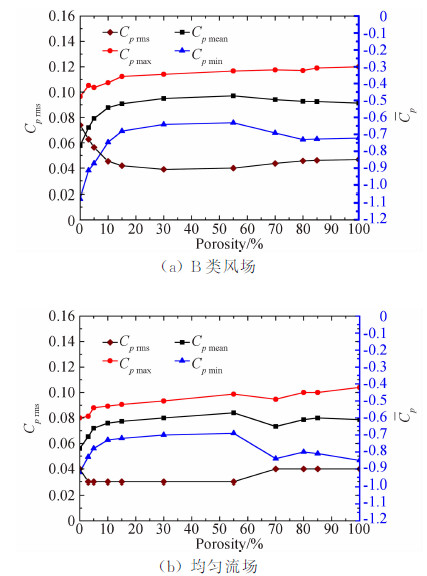 |
| 图 14 不同透风率风压系数代表值比较Fig. 14 Test result of different porosity |
通过计算流体力学软件Fluent对模型空塔(塔底无十字挡风板)与运行实塔内表面的风荷载进行模拟,并将数值模拟结果与刚性模型测压试验结果进行对比,以分析风洞试验方法存在的不足,如无法保证外表面相似,以及模拟塔内、外空气压差产生的向上抽力等不足。 3.1 计算方法
冷却塔内热交换系统包括填料及其支撑构件、进水竖井和淋水喷头等复杂结构,热交换过程又是气水两相质量和热量的传输过程,直接模拟该过程非常困难。考虑到填料层对冷却塔内流场的影响主要有两点:(1)塔内自下而上的抽力;(2)对气流的阻力。因此,可对计算模型进行简化,忽略塔内复杂的热交换系统,其两点主要影响可由设置适当的边界条件实现,其中,塔内自下而上的抽力可以通过风扇边界条件来模拟,而填料层的阻力和透风率可以通过多孔介质边界条件来实现。
塔内抽力的具体实现过程为在塔内设定一个无限薄的面,空气流经这个面时压强会出现跃升,且压强跃升量是速度的函数,通常可用多项式表达如下:
式中,Δp为压强跃升量;fn为多项式系数;U为速度。阻力可由多孔介质模型的经验公式定义,其实质为在动量方程中增加一个源项,它代表动量的消耗,表达式如下:
式中,Si表示第i个方程的源项;μ为粘性系数; D、C 为给定的矩阵。上述边界条件通过编写用户自定义函数(UDF)实现。
3.2 网格划分及参数设置建模时,采用CAD软件的PROE建立物理模型,将它导入GAMBIT软件进行网格划分。对于模型空塔,整个计算域长17.0m、高2.5m、宽3.0m,与风洞试验段尺寸保持一致,划分网格时将它分为内、外两个区域,内区长1.0m、宽1.0m、高1.0m,网格间距0.012m,外区流场网格间距0.05m,总网格数约为130万,如图 15所示。冷却塔内、外表面及地面都设有边界层,首层高度0.003m,高度增加因子为1.02,总高度为0.018m。冷却塔表面边界层网格划分如图 16所示。
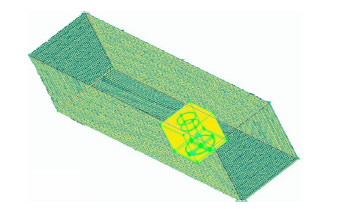 |
| 图 15 整体网格图Fig. 15 Grid of globe |
 |
| 图 16 冷却塔壁面边界层网格划分Fig. 16 Mesh of boundary layer of wall surface |
计算区域及边界条件如图 17所示。入口处采用速度入口边界条件,来流风速v=14m/s,风场条件与风洞模拟结果尽可能保持一致,平均风速剖面指数α=0.16,湍流度剖面计算表达式为Iu=A(z/H)-α-0.05,其中A为常数,z为离地高度,H为大气边界层厚度,离地高度30m处的湍流强度为16%,指定的平均风速和湍流度剖面可通过编写用户自定义函数(UDF)在边界条件中实现。出口处采用自然出流边界条件,流量权重为1。计算域顶部及左右侧壁采用自由滑移壁面边界条件,地面及冷却塔壁面采用无滑移壁面边界条件。经多次试验比较,取粗糙度常数为0.5,粗糙度平均高度为0.0008m。计算域控制方程的离散方法采用有限体积法,时间、空间离散格式分别为二阶迎风差分和二阶中心差分离散格式,计算模型选取RNG k-ε控制方程和非平衡壁面函数,压力、速度耦合采用Simple算法。
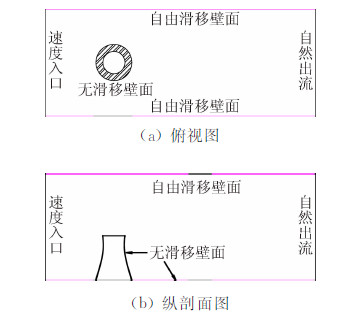 |
| 图 17 计算区域及边界条件Fig. 17 Calculation region and boundary conditions |
运行实塔计算模型的几何尺寸为实塔的几何参数,并考虑了塔底的十字挡风板。计算域长3000m、高600m、宽1200m,将其分为内、外两个区域来划分网格,内区为圆柱型,直径d=250m。多孔介质边界条件中,竖向惯性阻力系数取为16m-1,径向为160m-1,填料层开孔率为85%,风扇边界条件的压强跃升量设为130Pa。其它边界条件与计算参数的设置与模型空塔计算工况一致。
3.3 计算结果与分析图 18(a)所示为模型空塔内表面风压CFD模拟结果。可以看出:并不是所有高度的内压沿环向均匀分布,这种不均匀性在塔底尤为突出,其原因在于气流从塔底进入塔内,随后撞击在背风区的内壁上,使得该区域的负压急剧减少,甚至出现微正压;最大风压系数为-0.25,最小风压系数为-0.75,二者均出现在塔底,它们之间的偏差大小反应塔底内压沿环向分布的非均匀程度;除塔底外,风压系数沿高度基本均匀分布,波动范围在0.1以内;风压系数均值为-0.56,与风洞试验结果-0.52基本一致。由此可见,不管是内压大小还是分布特征,数值模拟结果均与风洞试验基本一致,表明刚性模型试验忽略模拟外表面对内压测试结果基本没有影响。从图 18(b)可以看出塔内流场分布并不均匀,在塔底入口处有较大的回流区,其产生原因是气流从塔底进入塔内,撞击在背风区内壁上的气流沿内壁向上爬升,由于喉部附近截面减小,气流上升受到阻滞,部分气流被迫沿迎风侧的内壁流回塔底,形成旋涡。
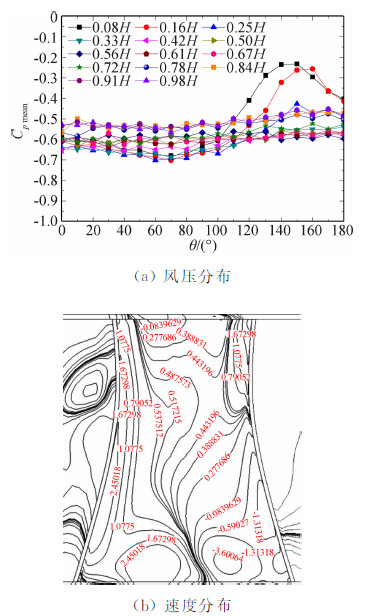 |
| 图 18 模型空塔数值计算结果Fig. 18 Result of numerical simulation for model |
图 19(a)为运行实塔内表面风压CFD模拟结果。可以看出:塔底风压沿环向均匀分布,没有在180°圆周角出现“突变”,但0.30H~0.50H之间的风压沿环向分布略有不均匀;内压沿高度基本呈均匀分布,波动范围在0.1之内;整体均值为-0.47,与风洞试验的-0.51基本一致。由此可见,不管是内压大小还是分布特征,数值模拟结果均与风洞试验基本一致,表明刚性模型试验忽略冷却塔运行过程中产生的向上抽力对内压测试结果基本没有影响。此外,运行实塔塔内风速分布较为均匀,且没出现明显的回流区(图 19(b))。
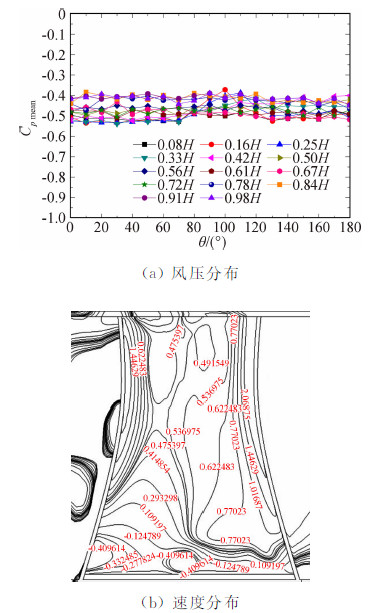 |
| 图 19 运行实塔数值计算结果Fig. 19 Result of numerical simulation for prototype |
通过刚性模型风洞试验和CFD 数值模拟对某220m 高冷却塔内表面风荷载特性进行了研究。计算得到的空塔和运行实塔内表面风压系数均值与试验数据基本一致,验证了数值计算的可靠性;反过来,数值计算考虑了冷却塔外表面以及冷却塔运行时内、外空气压差产生的向上抽力,其结果表明该两种因素对冷却塔内压的影响不大,表明风洞试验忽略这两种因素并无不妥。通过进一步的试验研究,发现:冷却塔内表面风压对试验风速大小、风向角不敏感;在塔底设置十字挡板后,塔内风压略有减小,风压沿环向、高度分布的均匀性更好;内压受填料层透风率影响较大,内压绝对值随透风率的增加略有减小,但当透风率大于10%后变化较小。总的来说,内表面风压系数沿环向、高度基本不变,B类风场中,平均风压系数约为-0.50,脉动风压系数约为0.045;均匀流场中,平均风压系数约为-0.61,脉动风压系数约为0.035。
由于风洞试验难以模拟冷却塔内气水两相质量和热量的传输过程,而CFD数值模拟较适用开展此类研究,但本文CFD模拟对气水两相流进行了简化处理,下一步应提高冷却塔运行时传热传质过程的模拟精度,以得到与实际更为接近的内压分布。
| [1] | GB/T 50102-2003. Code for cooling design of industrial circulating water[S]. (in Chinese) GB/T 50102-2003. 工业循环水冷却设计规范[S]. |
| [2] | DL/T 5339-2006. Technical regulation for hydraulic design of fossil fuel power plant[S]. (in Chinese) DL/T 5339-2006. 火力发电厂水工设计技术规定[S]. |
| [3] | Zhao Lin, Li Pengfei, Ge Yaojun. Numerical investigation on performance of super large cooling towers under equivalent static wind load[J]. Engineering Mechanics, 2008, 25(7):79-86. (in Chinese)赵林, 李鹏飞, 葛耀君. 等效静风荷载下超大型冷却塔受力性能分析[J]. 工程力学, 2008, 25(7):79-86. |
| [4] | Sun Tianfeng, Zhou Liangmao. A full-scale and wind-tunnel study of wind pressure distribution around a ribless hyperbolic cooling tower[J]. Acta Aerodynamica Sinica, 1983, (4):68-76. (in Chinese)孙天风, 周良茂. 无肋双曲线型冷却塔风压分布的全尺寸测量和风洞研究[J]. 空气动力学学报, 1983, (4):68-76. |
| [5] | Kasperski M, Niemann H J. On the correlation of dynamic wind loads and structural response of natural-draught cooling towers[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1988, 30:67-75. |
| [6] | Li Pengfei, Zhao Lin, Ge Yaojun, et al. Wind tunnel investigation on wind load characteristics for super large cooling towers[J]. Engineering Mechanics, 2008, 25(6):60-67. (in Chinese)李鹏飞, 赵林, 葛耀君, 等. 超大型冷却塔风荷载特性风洞试验研究[J]. 工程力学, 2008, 25(6):60-67. |
| [7] | 张陈胜. 大型双曲冷却塔风荷载的数值模拟研究[D]. 杭州:浙江大学, 2008. |
| [8] | Shen Guohui, Zhang Chensheng, Sun Bingnan, et al. Numerical simulation of wind load on inner surface of large hyperbolic cooling tower[J]. Journal of Harbin Institute of Technology, 2011, 43(4):104-108. (in Chinese)沈国辉, 张陈胜, 孙炳楠, 等. 大型双曲冷却塔内表面风荷载的数值模拟[J]. 哈尔滨工业大学学报, 2011, 43(4):104-108. |
| [9] | Bao Kanyuan, Shen Guohui, Sun Bingnan. Numerical simulation of mean wind load on large hyperbolic cooling tower[J]. Acta Aerodynamica Sinica, 2009, 27(6):650-655. (in Chinese)鲍侃袁, 沈国辉, 孙炳楠. 大型双曲冷却塔平均风荷载的数值模拟研究[J]. 空气动力学学报, 2009, 27(6):650-655. |
| [10] | 余关鹏. 大型双曲冷却塔风荷载特性和风致干扰效应研究[D]. 杭州:浙江大学, 2010. |
| [11] | Shen Guohui, Yu Guanpeng, Sun Bingnan, et al. Analysis of wind load on large hyperbolic cooling tower considering interaction between internal and external pressure[J]. Acta Aerodynamica Sinica, 2011, 29(4):339-446. (in Chinese)沈国辉, 余关鹏, 孙炳楠, 等. 考虑内外压共同作用的大型冷却塔风荷载分析[J]. 空气动力学学报, 2011, 29(4):339-446. |
| [12] | Diver M. Large cooling towers the present trend[J]. Journal of Structural Engineer, 1977, 10(55):130-137. |
| [13] | Sollenberger N J, Billington D P. Wind loading and response of cooling towers[J]. Journal of the Structural Division, ASCE, 1980, 103(3):601-621. |
| [14] | Scanlan R H, Leonard J F. Turbulent winds and pressure effects around a rough cylinder at high Reynolds number[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1982, 9:207-236. |
| [15] | Kawarabata Y, Nakae S, Harada M. Some aspects of the wind design of cooling towers[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1983, 14:167-180. |
| [16] | Zhai Zhiqiang, Zhu Keqin, Fu Song. Model experiment for the influence of cross-wind on the air flow field in natural draft dry-cooling tower[J]. Journal of Experimental Mechanics, 1997, 12(2):306-311. (in Chinese)翟志强, 朱克勤, 符松. 横风向对自然通风干式冷却塔空气流场影响的模型实验研究[J]. 实验力学, 1997, 12(2):306-311. |