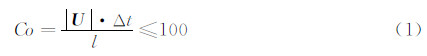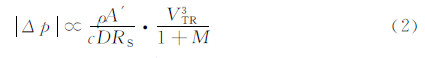0 引 言
高速列车驶入隧道时,在车头前隧道内产生的压缩波以近似声速向隧道出口端传播,到达隧道出口端后大部分反射形成膨胀波,少部分向洞外折射形成洞口微气压波。微气压波含有大量的低频波,强度较大时会产生音爆,对隧道周围环境和居民产生严重影响,因而带来环境问题。有关微气压波的研究起始于日本,系统的研究形成了一系列成果和相应的减缓措施[1, 2]。随着高速铁路的发展,欧洲、韩国等国家也开始关注该类空气动力学问题,开展了不同高速铁路特点下的微气压波研究[3, 4, 5, 6, 7, 8, 9]。在我国高速铁路发展过程中,吸取了外国特别是日本的经验教训,对微气压波问题较为重视,取得了许多有益的成果[10, 11, 12, 13, 14, 15]。
随着高速列车的速度进一步提高,在日本新干线上发现当高速列车驶入和驶出隧道时,隧道入口和出口附近也能观测到直接由隧道端口辐射出的低频(10~20Hz)脉冲波,称为隧道进口波和出口波[16]。从日本学者的研究来看,与洞口微气压波相比,隧道进/出口波不涉及在洞内传播这一环节,几乎不会受到非线性特性的影响,尽管强度较弱,但仍属次声波范畴,其危害与洞口微气压波一样,主要体现为隧道端口附近的轰鸣声、附近房屋窗框/百页窗等的剧烈振动引发的“喀喇”声。随着高速列车速度进一步提高,隧道进/出口波现象愈加明显,造成的环境问题也将更加严重[17]。目前,对隧道进/出口波的研究主要是以日本新干线技术路线为对象,采用试验研究、气动声学理论分析和数值模拟三种方法进行研究。M Iida等人[18, 19, 20]和MSHowe[21]应用单极子声源辐射理论建立了隧道进口波的理论预测模型,解释了进口波的基本特征,为隧道进/出口波的研究奠定了一定基础。但由于气动声学理论模型无法准确表述列车近场压力的影响,上述模型的预测结果与试验结果偏差较大。M Iida等人[20]利用二维无粘模型对旋成体列车模型过隧道的进口波进行了数值模拟研究,其结果在列车头部附近与试验结果吻合情况较好,但由于高速列车周围的流场是复杂的三维湍流流动,其列车尾部进口波的计算结果与试验结果之间的误差较大。需要指出的是上述研究中,均采用了旋成体列车模型,与实际的列车和隧道结构相差较远。在我国尚未见到他人研究隧道进/出口波的公开报道。
本文依据我国CRH380A高速列车,采用基于CFD软件的三维非定常可压缩湍流模型,在与日本试验和理论研究结果对比基础上,研究列车进入隧道过程的流动特性,揭示进口波的基本特性,为今后进一步深化研究提供基础。
1 问题描述和定解条件 1.1 物理问题和计算模型当CRH380A高速列车以380km/h的速度通过隧道时,运动马赫数为0.31,基于列车轨面以上高度的雷诺数高达107数量级,其外部的空气流动为三维非定常可压缩的湍流流动。本文忽略单洞复线隧道内的内部建构筑物,将隧道简化为光滑半圆管模型,横断面直径D=13.3m,横截面面积FTU=100m2,长LTU=58.6D,线间距0.38D;CRH380A高速列车为忽略转向架和受电弓等部件的光滑表面模型,轨面以上车高hT=0.28D,长LTR=7.74D;车/隧模型的阻塞比为0.108。
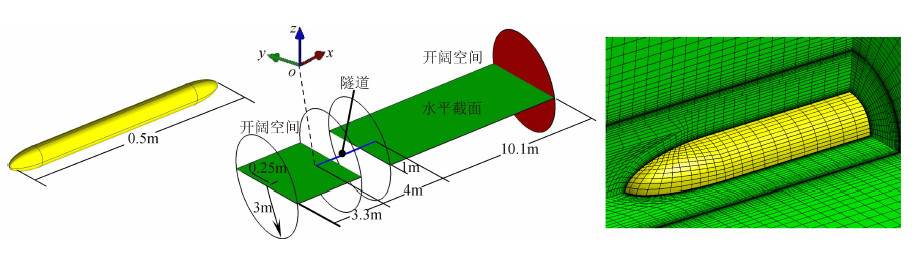
取隧道空间及端口外的开阔空间构成计算区域,两者横截面为同心圆弧,开阔空间半径15D。以隧道入口平面内隧道中心线与轨面的交点为坐标原点,高速列车前进方向为x正方向,铅垂向上为z正方向,按右手准则建立直角坐标系,如图 1(a)所示。图 1中的计算区域可同时研究隧道进出口波。本文仅介绍隧道进口波,隧道出口波将另行撰文。
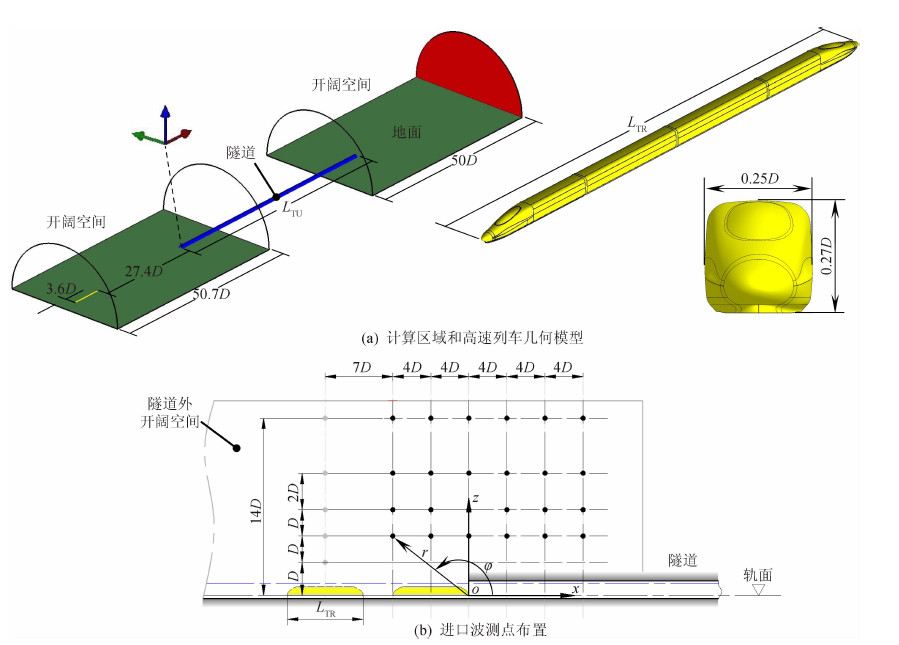 |
| 图 1 计算模型和进口波测点布置Fig. 1 Numerical model and monitoring points of the tunnel entry wave |
若研究中保持模型几何相似且马赫数与实际情况相等,则几何上对应位置的压力一致,但频率会成比例放大[1, 19]。研究采用1∶10缩比模型,高速列车的速度与实际情况保持一致,因此研究中的雷诺数较实际情况小一个数量级,从而降低了网格总体规模。为避免数值模拟中列车突然运动引起的不符合物理实际的压力波动,应用了光滑启动技术[22]。高速列车匀速运动后离隧道端口应保持一定距离,以避免其非均匀运动对进口波观测造成影响,因此图 1(a)中高速列车在求解之初距离隧道较远。结果分析中定义高速列车到达隧道入口端时刻为t=0,在流场中布置图 1(b)所示的观测点研究隧道进口波。
1.2 求解方程及定解条件高速列车外部的空气按有粘完全气体处理,采用SST k-ω高雷诺数湍流模型数值求解CRH380A高速列车外部的三维非定常可压缩湍流流动,即求解连续性方程、动量方程、能量方程、状态方程和湍流模型方程[23]。在求解初始时刻,CRH380A高速列车处于静止状态,其周围流场也静止,按海平面国际标准大气(ISA)确定参考压力和温度状态,湍流物理量处处为0。
高速列车通过隧道时的边界区域如图 1(a)所示。其中高速列车表面为无滑移运动壁面,其运动速度在求解过程中由0增加至匀速运动的车速VTR。隧道表面和地面为无滑移静止壁面,被计算区域流体包裹的隧道部分设为无滑移挡板边界,两侧均为无滑移静止壁面。这些固体壁面均为绝热边界,湍流物理量用非平衡壁面函数法处理。隧道外开阔空间的各表面为常温常压的黎曼边界,湍流物理量为0。
2 数值计算方法 2.1 网格划分 2.1.1 网格划分整体策略应用STAR-CD软件的ASI技术求解高速列车通过隧道问题,整个计算区域可分为静止和运动两大部分,两者之间的交界面构成滑移界面。数值求解时,在列车远前方的计算区域边界上,运动网格不断逐层移出;在列车远后方的计算区域边界上,运动网格不断逐层添加进计算区域;每个计算时间步内,动静网格通过解耦—运动—耦合—求解,实现动网格的计算。因此,网格划分中将动静两部分作为两个单独的“体”处理,并将列车周围区域从运动网格中分出来,进行适度加密。这样形成三个体的多块网格划分方法,其中列车周围区域完全包含于运动部分之中,两者之间的交界面用网格耦合处理。图 2为多块网格划分的整体规划示意图。
 |
| 图 2 网格分布规划与多块网格划分策略Fig. 2 Layout of grid distribution and the strategy of multi-block grid generation |
高速列车表面法向第一层网格的厚度按照y+=50取定,流向和展向网格尺度分别为Δx+=(9~152)y+,Δz+=(5~52)y+。
2.1.3 求解稳定性和时间步长非定常问题的求解中,尽管隐式时间离散格式是无条件稳定的,但实际计算中为减小误差累积,应满足稳定性条件[24],即:
其中,Co为Courant数,|U|= u cell+a,u cell为某点速度,a为当地声速,l为网格特征尺度。本文用列车表面最小网格尺度和固壁法向第一层网格厚度估算时间步长Δt,其典型值为0.018LTR/VTR。 2.1.4 运动网格步长动网格运动的速度和方向与列车相同,在求解的一个时间步长Δt内向前移动δx=VTRΔt。计算区域的边界在求解过程中保持不变,添加和删除的网格在其运动方向(流向) 上的步长Δx为均匀分布,并满足Δx=nδx=nVTRΔt,即n个时间步运动一层网格。图 3为典型的网格划分结果示例,网格划分的总体规模约为420万。
 |
| 图 3 CRH380A通过隧道数值模拟的网格划分示例Fig. 3 General grid generation of CRH380A high-speed train passing throughatunnel |
列车光滑启动阶段,由于列车和动网格运动速度的不均匀变化,采用课题组研制的软件结合ASI技术实现。用PISO算法求解压力速度耦合问题,各方程时间项的离散用欧拉隐格式,并用中心差分格式离散扩散项,用MARS格式离散对流项。用代数多重网格法(AMG)求解离散的代数方程组。
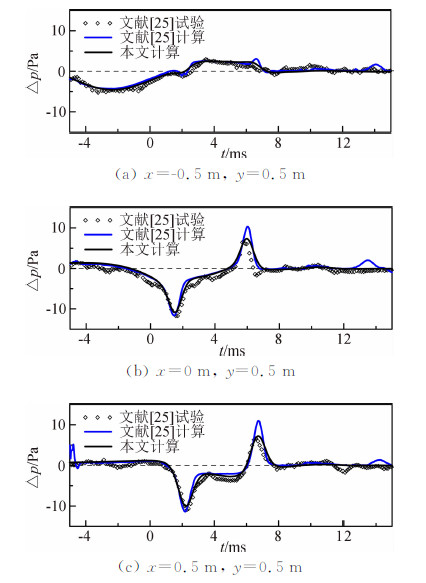
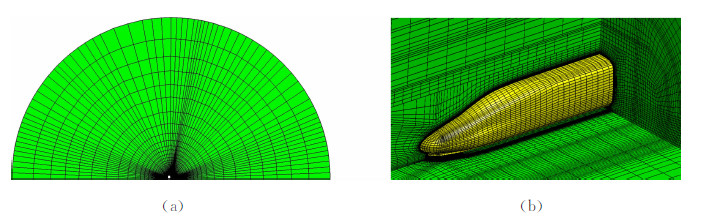
3 计算结果和讨论 3.1 数值方法验证以文献[25]关于旋成椭圆体的模型试验和数值模拟结果检验本文数值计算方法的正确性。计算条件与文献模型试验保持相同,即隧道直径0.1m,列车模型直径42.7mm,计算区域与网格划分如图 4所示。除列车模型和隧道壁面为无滑移静止壁面外,其余开阔空间各表面均为常温常压的黎曼边界。图 5为三个典型测点处本文计算结果与文献[25]结果的对比。由图 5可见,本文计算结果与试验数据更为吻合,说明三维流动模型能够提高计算精度,从而验证了本文数值方法的正确性。
 |
| 图 4 数值方法验证采用的计算模型和网格Fig. 4 Solution domain and grid generation in the numerical method verification study |
图 5也表明了列车鼻尖进入隧道时产生的进口波为负压力脉冲,当传播过一定距离r到达x≥0(图 1中φ≤π/2)的测点时,压力降低;平直车身驶入隧道时压力短暂恢复;列车尾尖进入隧道时产生的进口 波为正压力脉冲,当传播到x≥0的测点时,压力升高;尾部驶入隧道后压力逐渐恢复。进口波沿流向反向传播到x<0(φ>π/2)的区域时,情况有所不同。这是由于高速列车在明线上运行时,外部的压力分布可分为近场区的流体力学压力波动和远场区的低频噪音两部分,前者与离开列车的距离的平方成反比,后者与离开列车距离的均方根成反比[26]。对于x<0的区域,首先受到列车通过测点时的近场压力的影响,进口波传播到测点时,与近场压力互相叠加。由于进口波幅值较小,从图 5(a)中可见进口波对测点 -0.5m,0,0.5m 压力波动的影响幅度要小得多。这表明仅在距离列车/隧道较远、近场压力衰减较明显的x≥0区域时,才能观察到进口波对测点压力的影响,并且文献[25]将这种现象称为进口波的指向性,即隧道进口波在x≥0(φ≤π/2)的区域较为明显,而在x<0(φ>π/2)的区域影响减弱。
3.2 高速列车近场和远场压力波动特征应用前述经过验证的数值方法研究CRH380A高速列车以380km/h的速度通过隧道时的情况。
虽然隧道进口波是高速列车驶入隧道时列车与隧道共同作用的结果,但了解高速列车进入隧道前明线上运行时其外部开阔空间的压力波动情况,有助于认识隧道进口波的基本特性。图 6从侧面和俯视两个角度给出了CRH380A高速列车距隧道入口15D(t=-0.95s)时周围的压力分布。由图 6可见,由于此时相当于高速列车在明线上稳定运行,列车表面和周围的压力分布呈现典型的明线绕流特征:列车头部周围的流动属于“源流”,尾部周围的 流动属于“汇流”[14];车头鼻锥前方是正压区,后部直至尾车鼻锥均受负压区影响,尾车鼻锥后部又形成正压区。图 6也说明了可将高速列车头部和尾部分别作为运动的单极子声源,列车明线上运行时其强度并不发生变化,因此也不会产生压力脉动。图 6中Cp=Δp/ 0.5ρV2TR 为压力系数,且为便于观察流场形态,速度矢量箭 头仅代表速度的方向,速度大小由色彩表示。
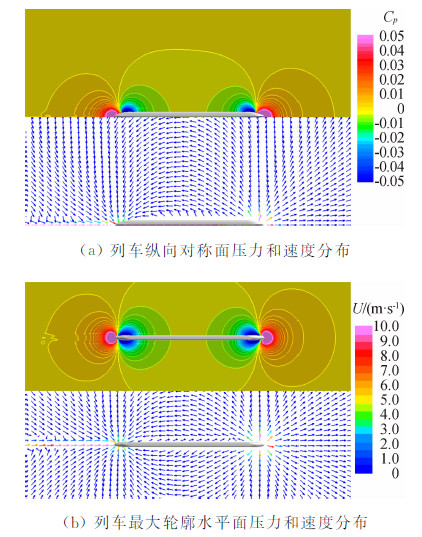 |
| 图 6 高速列车明线运行时周围的压力和速度分布Fig. 6 Distribution of pressure and velocity around the high-speed train when running in open section |
为进一步说明列车周围的近场和远场压力特征,图 7给出了列车纵向中心平面内自车体上表面铅垂向上远离列车时的压力变化。由图 7可见,CRH380A曲线车头、车尾处压力变化剧烈,其中车头最大/最小压力值为6.25kPa/-1.27kPa,车尾为1.26kPa/-1.01kPa,说明这些区域存在较大的压力梯度。由于司机室窗户处形成较小的“鼓起”形态(见图 1),所以此处压力出现幅度较小的极大值与极小值。平直车身压力逐渐恢复,但未恢复到Δp=0Pa的水平,最高到-0.02kPa。离开列车表面后,车体周围流场的压力幅值逐渐减小。z<0.4D时流场压力波动基本上仍能反映出列车上表面的压力分布细微特征,如司机室前玻璃窗的凸起引起的压力波动,表明在这个区域内列车近场压力的影响仍较显著。
 |
| 图 7 高速列车明线运行时近场和远场的压力波动Fig. 7 Vertical pressure variation stepping from the high-speed train surface |
垂向距离进一步增加时,这种细微特征消失了,但车体周围压力分布的主要特征仍保持得较好,即列车曲线头部先正后负、平直车身压力恢复、曲线尾部先负后正的压力变化过程,说明列车近场压力的影响逐渐减弱。当z>2D时,压力变化已趋平坦,至z=5D时在图示的压力标尺下基本为一直线,表明列车近场压力已经较弱了。因此距离列车越远,压力波动的幅值越小,列车近场压力的影响越小,这与文献[26]所述变化规律相符。
如果没有隧道,高速列车将在明线上一直匀速运动,其周围的压力分布形态也将跟随列车一起向前推进,线路上任意位置上的压力波动沿垂向的变化均如图 6和图 7所示,因此图 7也可看作列车经过相应测点的压力波动,即将图 7横坐标当作时间轴t,t=tH时以速度VTR运动的高速列车的头部鼻尖通过测点所在位置,t=tT时尾部鼻尖离开测点所在位置。如此类比有助于认识和分析高速列车通过隧道时,相同垂向位置z处由于隧道因素而引起的压力波动。
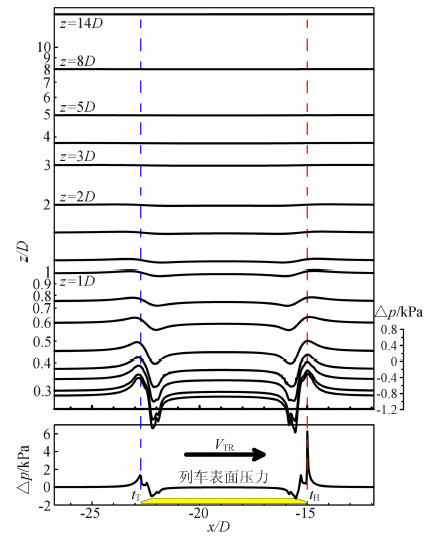
3.3 高速列车隧道进口波的波形特征随着高速列车逐渐驶向隧道,其周围流场逐渐受到隧道的影响。图 8和图 9分别从垂向和流向两个角度展示了y=0平面内隧道入口前后各测点处的压力波动情况。高速列车头部和尾部进入隧道时均会产生隧道进口波,并以当地声速向四周传播,图 8中tHW、tTW分别为列车头部和尾部鼻尖驶入隧道产生的进口波传播到z=2D直线上各测点的时刻,时间差δt=tHW-tTW=tH-tT=LTR/VTR是整列车通过测点所需时间。注意到图 7与图 8、图 9中的压力标尺范围并不相同,因此后者x≤0各处的压力波动与图 7所示的压力波动形态有差异。
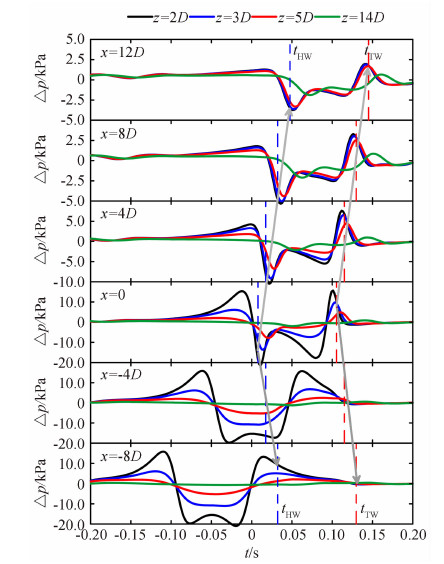 |
| 图 8 高速列车驶入隧道时隧道入口附近的压力波动Fig. 8 Pressure fluctuation near the entrance when the high-speed train running into the tunnel |
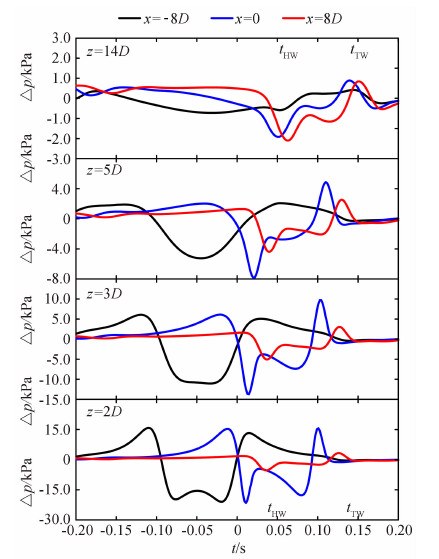 |
| 图 9 高速列车驶入隧道时沿流向的压力波动Fig. 9 Stream wise pressure fluctuation when the high-speed train running into the tunnel |
由图 8可见,t=0时刻CRH380A高速列车驶入隧道入口产生负压力脉冲,当传播到x>0同一流向位置不同垂向高度时使该处压力下降;车尾进入隧道时产生正压力脉冲,当传播到同一流向位置不同垂向高度时使该处压力升高。此即CRH380A驶入隧道时产生的进口波传播至测点时的基本特征。图 9进一步说明由于受到列车近场压力的影响,x<0区域各测点的压力波动形态明显有别于x≥0区域各测点。当z=2D时,列车通过x≤0各测点的压力波动幅值较大,进口波传播到测点引起的压力波动不明显;当z>2D时,由图 6和图 7可知此处列车近场压力已较为平坦,因此能够清晰地观察到进口波传播至测点后引起的压力变化。不过由于进口波在传播中也随着距离的增加而减弱,因此引起的测点压力变化幅值较低,如z=5D各测点由进口波引起的压力变 化为-8~5Pa,z=14D处为-2~1Pa。因此,对于x≤0的测点,压力波动是列车近场压力与进口波共同作用的结果,前者不具声波特征,后者是以声速传播的声波。隧道进口波展现出的这种对进口端两侧的不同影响,说明本文得出的高速列车隧道进口波具有指向性的特征,与文献[16, 17, 18, 19, 20]结论一致。
3.4 高速列车隧道进口波的传播特性图 10为CRH380A高速列车驶入隧道产生的进口波的传播特性。前已述及在距离隧道较远的区域进口波影响比较明显,考虑到其幅值随传播距离增大而衰减,因此图中缩小了压力标尺的范围。由图 10可清晰观察到列车驶入隧道产生的进口波向x≥0区域的传播,即车头驶入的进口波传播到测点时使其压力降低,车尾进口波传播到测点时使其压力升高,同时也说明了进口波的指向性。进口波传播到x<0区域时,也会使列车近场压力分布形态发生变化,但由于进口波幅值远小于近场压力,因此图中该区域的进口波传播特性并不明显。
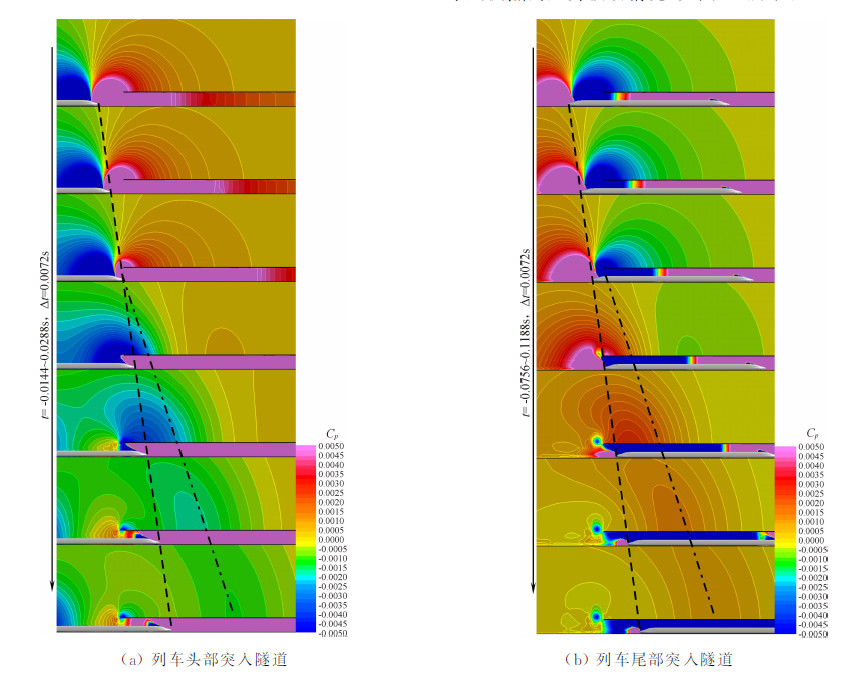 |
| 图 10 高速列车隧道进口波的传播特征Fig. 10 Propagation of the tunnel entry wave during the high-speed train running into the tunnel |
为进一步说明进口波对x<0区域的影响,在直线y=0、z=3D上x=-8D~8D范围内连续观察一
系列测点的压力波动情况,如图 11所示。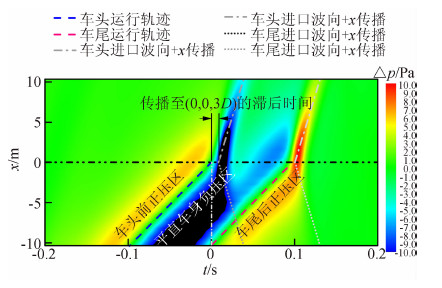 |
| 图 11 y=0,z=3D直线上x=-8D~8D范围内的压力波动Fig. 11 Pressure variation along the line x=-8D~8D, y=0,z=3D |
由图 11可见,CHR380A高速列车驶入隧道产生的正负压力脉冲传播到x≥0区域时,由于这些区域未受到列车近场压力波动的影响或影响较小,因此 能够从图中明显观察到以近似当地声速传播的进口波。而当进口波传播到x<0区域时,会与列车近场压力互相干涉、叠加,在x>-6m区域车头驶入的进口波使得近场较大的负压值减小,车尾驶入的进口波使较大的正压值略微减小;x<-6m时由于进口波幅值衰减,其对测点压力的影响减弱。这可理解为高速列车进口波的正负压力脉冲对x<0区域的列车近场压力有削峰平谷作用。
3.5 高速列车突入隧道进口波的产生过程线性声学理论分析结果表明[20],当高速列车在明线上运行时,运动的车头车尾单极子声源的强度不发生变化,其结果是不会产生压力脉动,即不会产生类似隧道进口波的声波,而当高速列车驶入隧道时才 会产生扰动而形成声波。声学理论可解释这一现象, 但不直观。本文结合三维流场特征揭示进口波产生过程。图 12表示了CRH380A高速列车以380km/h 的速度突入隧道时,列车表面、隧道表面和地面上的压力分布和三个断面x=-0.45D、0、0.45D上的气流速度变化情况。
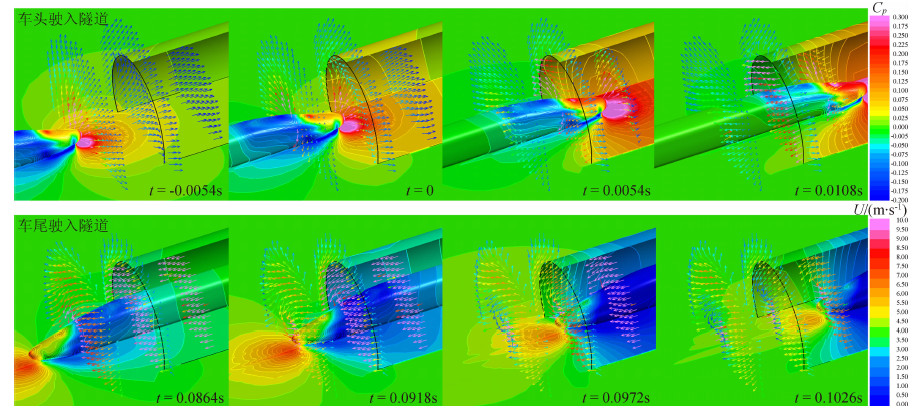 |
| 图 12 高速列车驶入隧道产生进口波的机理分析Fig. 12 Generation mechanism of entry wave when high-speed train entering the tunnel |
图 12表明,当高速列车即将驶入隧道前(t= -0.0054s),处于列车运行前方的空气(包括隧道内的空气在内)受到列车鼻锥前的“源流”流场的扰动,其运动方向与列车前进方向相同,距离列车越远受到扰动的速度和压力越微弱;在隧道端口边缘,气流有不太明显的绕过隧道壁面向外的流动。当列车到达隧道入口端时(t=0s),该处气流受到的扰动明显增强,形成以隧道端口边缘为起始的声源辐射;在距离隧道较远的区域观察,隧道入口作为静止的单极子声源被驶近的列车头部单极子声源激活,将向外辐射声波。与此同时,隧道内靠近入口的区域已经感受到了较强的车头前正压区的影响,压力急剧上升,在很短的流向距离上存在较大的压力梯度,表明即将形成隧道内的初始压缩波。当一部分列车曲线头部驶入隧道时(t=0.0054s),由于隧道壁面的限制,头部鼻锥对正前方一部分空气的推压作用增强,隧道内初始压缩波的强度逐渐增加。而此时受高速列车的流线型头部形状的影响,曲线头部与隧道之间环状空间的空气受到排挤,反向朝隧道入口外流动。随着列车曲线头部突入隧道,环状空间的面积逐渐减小,反向气流加速;当其到达隧道入口端时,会形成向外辐射的正压力脉冲波。这样一来,对隧道外的观测点来说,既观察到了运动的列车曲线头部单极子声源的突然消 失过程,又观察到隧道端口静止单极子声源的声辐射,但由于突然消失的头部压缩波强度大于隧道端口的声辐射强度,两者叠加就使隧道外部观测点感受到负的压力脉冲波。列车曲线头部完全驶入隧道后(t=0.0108s),环状空间的横截面积不再变化,气流不再加速,因此负压力脉冲波也即结束。
高速列车车尾驶入隧道的过程与此类似,但情况恰好相反。由图 12可见,随着列车曲线尾部驶入隧道,原来环状空间中被列车排挤反向流动的气流,由于环状空间的横截面积逐渐增加,速度逐渐减小,直至最后跟随列车尾部的尾流一同流入隧道。在此过程中,这部分气流扰动形成隧道入口端的静止单极子声源的声波辐射。同时,因为车尾驶入隧道时在隧道内形成膨胀波,因此对隧道外空间来说,观察到的是突然消失的运动的单极子膨胀波声源和静止声源辐射的声波,但前者的强度大于后者,因此隧道外观测点感受到的是正压力脉冲波。列车曲线尾部完全驶入隧道后,环状空间的横截面积不再变化,隧道外区域感受到的正压力脉冲波也即结束。
高速列车驶入隧道过程中形成的正压力脉冲和负压力脉冲构成了进口波的基本特征,如图 8、图 9所示。不过由于进口波总是表现为运动的列车曲线头部和尾部的声源辐射与进口端静止声源辐射的共同作用,其幅值并不大,在距离列车和隧道较近的区域存在列车近场压力波动的情况下,不易直接观察到进口波的形态。只有在距离隧道端口较远的区域,才可以在压力分布图中观察到进口波及其传播的特征,这也是图 10和图 12涉及的区域并不相同的原因。
3.6 列车速度对隧道进口波的影响为定量研究高速列车速度对隧道进口波的影响规律,本文研究了CRH380A以300、380、450、500km/h通过隧道时的情形。图 13为四种车速情况下三个典型位置的压力波动,表明在本文研究的速度范围内,隧道进口波波形的基本特征并不随列车速度的增加而改变,但幅值增大(x≥0区域)。其次,由于各种情况下均定义列车鼻尖突入隧道时刻为时间原点,因此车头鼻尖突入隧道的负压力脉冲到达测点的时刻是相同的,但车尾突入隧道的正压力脉冲到达测点的时刻随车速增加而提前。
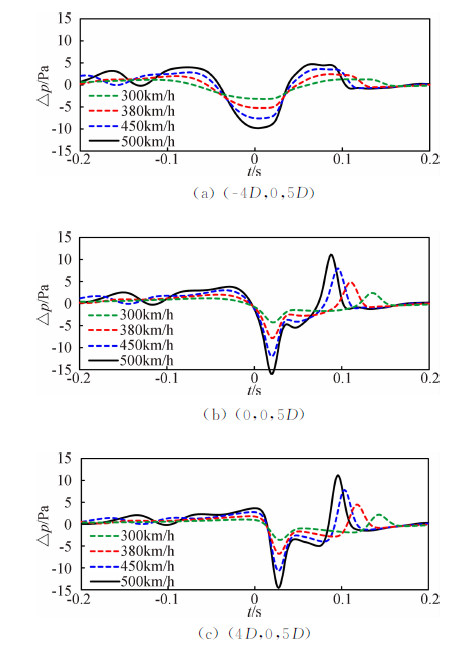 |
| 图 13 列车速度对隧道进口波的影响Fig. 13 Train speed dependency of tunnel entry waves |
以本文计算的隧道进口波的正负压力脉冲的峰值(绝对值)统计数据研究隧道进口波随列车速度变化的规律,结果如图 14所示。图 14表明本文计算的CRH380A高速列车隧道进口波的最大正压值与列车速度的3~3.3次方成正比,而最大负压值与速度的2.6~2.8次方成正比。文献[18, 19]对试验结果的分析说明隧道进口波的幅值与列车速度的三次方成正比关系,而Iida等人[20]的气动声学分析表明:
式中c为当地声速,A′为列车横截面积,RS为观测点据隧道端口的距离。式(2)表明在隧道和列车条件不变时,固定观测点处的隧道进口波幅值与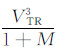 成正比。严格讲列车速度变化时其运动的马赫数也发生变化,因此进口波的幅值应近似与列车速度三次方成正比。同时,数值上ρA′~D~10、cRS~105,说明比例关系系数较小。以本文速度380km/h工况和5D高度测点即65.5m为例,有 |Δp| ∝3.51×10-5V3TR。考虑到高速列车速度的数值较大,一般达每小时数百公里,即VTR~100km/h,而进口波的最大正负压力值数值较小,一般为几十Pa,即Δp~10Pa,因此图 14中各拟合公式的列车速度的单位取“102km/h”,以避免拟合公式中的比例系数过小,在估算进口波幅值时引起额外的计算误差。此外,图 14中由于测点 4D,0,5D 较测点 0,0,5D 距隧道入口更远,因此也可说明隧道进口波幅值随观测点距隧道入口距离的增加而减小。
成正比。严格讲列车速度变化时其运动的马赫数也发生变化,因此进口波的幅值应近似与列车速度三次方成正比。同时,数值上ρA′~D~10、cRS~105,说明比例关系系数较小。以本文速度380km/h工况和5D高度测点即65.5m为例,有 |Δp| ∝3.51×10-5V3TR。考虑到高速列车速度的数值较大,一般达每小时数百公里,即VTR~100km/h,而进口波的最大正负压力值数值较小,一般为几十Pa,即Δp~10Pa,因此图 14中各拟合公式的列车速度的单位取“102km/h”,以避免拟合公式中的比例系数过小,在估算进口波幅值时引起额外的计算误差。此外,图 14中由于测点 4D,0,5D 较测点 0,0,5D 距隧道入口更远,因此也可说明隧道进口波幅值随观测点距隧道入口距离的增加而减小。
 |
| 图 14 最大压力值(绝对值)与列车速度的拟合关系Fig. 14 Speed dependency of the maximum pressure fluctuation (absolute value) of tunnel entry waves |
隧道进口波属于次声波范畴,其对环境的影响主要体现在其频域特性上。本文用傅氏变换对(0,0,3D)和(0,0,5D)两个典型测点的时域数据进行处理,用频谱幅值和声压级分析结果来说明隧道进口波的次声波特性及其对环境的影响,如图 15所示。
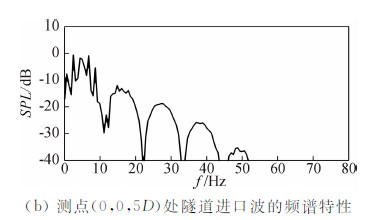 |
| 图 15 隧道进口波的频谱特性Fig. 15 Frequency spectrum of the tunnel entry waves |
由图 15可见,CRH380A高速列车在速度为380km/h时,尽管距离隧道越远频谱幅值越小,但是两测点处的频率均小于70Hz,这说明实车模型时隧道进口波的频率小于7Hz,从而表明了其次声波的特性。此外,声压级的幅值较小且呈现离隧道端口越远而越小的趋势,在(0,0,3D)处的最大值约为5dB。这是由于头尾部的流线型较好,而且我国隧道的横断面积较大,因而声压级较低,对环境的影响较小。 4 结 论
本文对CRH380A高速列车驶入隧道时诱发的隧道进口波进行了数值研究,得出以下结论:
(1) 与文献[25]试验数据和数值模拟结果的对比研究表明,本文建立的三维流动模型的数学物理模型合理,数值计算方法正确,计算精度更高。
(2) 高速列车头部和尾部驶入隧道时,分别向隧道入口外辐射负压力脉冲波和正压力脉冲波,从而形成隧道进口波。隧道进口波存在朝向列车运行方向的指向性,列车运行前方的隧道外区域要比其运行后方的区域感受到更明显的进口波。
(3) 高速列车驶入隧道产生的进口波幅值近似与列车速度的三次方成正比,与观测点距隧道入口距离成反比。
(4) 隧道进口波作为次声波,其主频小于70Hz,对应实际列车模型时小于7Hz。隧道进口波的频率和频谱幅值均随着距隧道入口的距离而减小。CRH380A高速列车因其头尾部的流线型较好,因此驶入隧道诱发的进口波的声压级较低,对外部环境的影响较小。
| [1] | Ozawa S. Studies of micro-pressure wave radiated from a tunnel exit[R]. Japanese National Railways, Railway Technical Research Institute Report, 1979, 1121:1-92. (in Japanese) |
| [2] | Ozawa S. Present situation and future outlook of aerodynamics and aeroacoustics problems of high speed trains[R]. Quarterly Report of Railway Technical Research Institute, 1992, 23(1):33-38. |
| [3] | Schetz J A. Aerodynamics of high-speed train[J]. Annual Review of Fluid Mechanics, 2001, 33:371-414. |
| [4] | Raghunathan R S, Kim H D, Setoguchi T. Aerodynamics of high-speed railway train[J]. Progress in Aerospace Sciences, 2002, 38:469-514. |
| [5] | Yoon T S, Lee S, Hwang J H, et al. Prediction and validation of the sonic boom by a high-speed train entering a tunnel[J]. Journal of Sound and Vibration, 2001, 247(2):195-211. |
| [6] | Ehrendorfer K, Reiterer M, Sockel H. Numerical investigation of the micro pressure wave[G]. TRANSAERO-a European initiative on transient aerodynamics for railway system optimization:notes on numerical fluid mechanics and multidisciplinary design (NNFM), 2002, 79:321-341. |
| [7] | Vardy A E. Generation and alleviation of sonic booms from rail tunnels[J]. Engineering and Computational Mechanics, 2008:107-119. |
| [8] | Tielkes Th. Aerodynamic aspects of maglev systems[C]//MAGLEV'2006:The 19th International Conference on Magnetically Levitated Systems and Linear Drives. Dresden, Germany:Transrapid International GmbH und Company KG, 2006:641-649. |
| [9] | Tielkes Th, Kaltenbach H J, Hieke M, et al. Measures to counteract micro-pressure waves radiating from tunnel exits of DB's new Nuremberg-Ingolstadt high-speed line[J]. Noise and Vibration Mitigation, 2008, 99:40-47. |
| [10] | Mei Yuangui, Xu Jianlin, Geng Feng, et al. Numerical investigation of micro-pressure waves radiated from a tunnel exit based on the model of radiating of circular piston in the infinite plat[J]. Journal of the China Railway Society, 2006, 28(4):74-78. (in Chinese)梅元贵, 许建林, 耿烽, 等. 基于无限大障板圆形活塞辐射原理的隧道微气压波计算方法[J]. 铁道学报, 2006, 28(4):74-78. |
| [11] | Luo Jianjun, Gao Bo, Wang Yingxue. Numerical study on tunnel-hood when high-speed train passing a tunnel[J]. Acta Aerodynamica Sinica, 2003, 20(9):376-381. (in Chinese)骆建军, 高波, 王英学. 高速列车突入隧道与缓冲结构时的数值模拟[J]. 空气动力学学报, 2003, 20(9):376-381. |
| [12] | Wan Jianyu. Tunnel aerodynamics in high-speed railways[C]//Proceedings of 2006 China international symposium on high speed railway tunnels. China Railway Publishing House, 2006:74-86. (in Chinese)王建宇. 高速铁路隧道空气动力学若干问题探讨[C]//2006中国高速铁路隧道国际技术交流会论文集. 中国铁道出版社, 2006:74-86. |
| [13] | Tian Hongqi. Aerodynamics of trains[M]. Beijing:China Railway Publishing House, 2007. (in Chinese)田红旗. 列车空气动力学[M]. 北京:中国铁道出版社, 2007. |
| [14] | Mei Yuangui, Zhou Zhaohui, Xu Jianlin. Aerodynamics of high-speed railway tunnel[M]. Beijing:Science Press, 2009. (in Chinese)梅元贵, 周朝晖, 许建林. 高速列车隧道空气动力学[M]. 北京:科学出版社, 2009. |
| [15] | Wang Yingxue, Gao Bo, Zhu Dan, et al. Control technology of Aerodynamics effect of high speed railway tunnel[M]. Beijing:Science Press, 2012. (in Chinese)王英学, 高波, 朱丹, 等. 高速铁路隧道空气动力效应控制技术[M]. 北京:科学出版社, 2012. |
| [16] | Tanaka Y, Kikuchi K, Iida M, Takahashi R. Field measurement of pressure waves radiated from tunnel portals at train entry/exit[J]. Transactions of the Japan Society of Mechanical Engineers (B Series). 2001, 67:2470-2477. |
| [17] | Iida M. Current status of research and development on railway aerodynamics[R]. Railway Technical Research Institute Report, 2011, 25(11):1-4. (in Japanese) |
| [18] | Iida M, Kikuchi K, Fukuda T. Pressure wave radiated from a tunnel entrance when a train enters a tunnel[C]. Meeting of Japan Society of Fluid Mechanics, 1999:147-148. |
| [19] | Iida M, Tanaka Y, Kikuchi K, Fukuda T. Characteristics of the pressure wave radiated from an entrance portal when a train enters a tunnel[J]. Theoretical and Applied Mechanics.2001:371-377. |
| [20] | Iida M, Kikuchi K, Fukuda T. A pressure wave radiated from a tunnel entrance when a train enters a tunnel[C]. Caserta A. 10th International Symposium on the Aerodynamics and Ventilation of Vehicle Tunnels. Boston:BHRA, 2000:779-797. |
| [21] | Howe M S. On the infrasound generated when a train enters a tunnel[J]. Journal of Fluids and Structures, 2003, 17:629-642. |
| [22] | Yo-Cheon Ku, Joo-Hyun Rho, Su-Hwan Yun, et al. Optimal cross-sectional area distribution of a high-speed train nose to minimize the tunnel micro-pressure wave[J]. Structural and Multidisciplinary Optimization, 2010, 42:965-976. |
| [23] | CD-adapco Group. STAR-CD version 4.08 Methodology[M]. Computational Dynamics Limited, 2008:2.1-2.35. |
| [24] | CD-adapco Group. STAR-CD version 4.08 User guide[M]. Computational Dynamics Limited, 2008:5.8-5.9. |
| [25] | Iida M, Fukuda T, Kikuchi K. Numerical analysis of the pressure wave radiated from the entrance when a train enters a tunnel[J]. Transaction of the Japan Society of Mechanical Engineers, 2000, 66(651):2861-2868. |
| [26] | Kikuchi K, Takasaki T, Iida M. Characteristics of low-frequency pressure waves radiated from a train passing an open section[J]. Journal of Environment and Engineering, 2007, 2(2):359-370. |