0 引言
20世纪以来,随着现代高强材料和施工技术的发展,大跨度桥梁尤其是悬索桥、斜拉桥在世界各地相继兴建[1]。现代大跨度桥梁的代表作有1997年建成的主跨1624 m的丹麦大贝尔特东桥、1998年建成的主跨1 991 m的日本明石海峡大桥和即将兴建的主跨3 300 m的意大利墨西拿海峡大桥等,而1999年建成的主跨1 385 m的江阴长江大桥、2005年建成的主跨1 490 m的润扬长江大桥南汊桥以及2008年建成的主跨1 088 m的苏通大桥等,标志着中国建设大跨度桥梁的能力已经迈入世界前列。然而随着现代大跨度桥梁跨径的不断增大,桥塔的高度也随之显著增加。大跨度斜拉桥挂索之前的裸塔在水平向没有约束,风荷载是裸塔结构的主要控制荷载之一,且随着高度的增加,裸塔结构的风振响应也逐渐增大。由于自然风中紊流成分的存在,裸塔在脉动风作用下的抖振是其不可避免的振动形式之一[2]。虽然不会引起桥塔的失稳或强度破坏,但过大的抖振响应会影响施工人员及机械的安全,同时也会导致桥塔结构的疲劳破坏,缩短其使用寿命。因此,有必要采取有效措施对大跨度斜拉桥裸塔结构的抖振响应进行控制,以提升其抗风安全性。
结构被动控制是国内外研究最早、应用最多的一种振动控制方式,目前在理论和应用上都取得了很多成果。TMD作为结构被动控制的主要形式之一,国内外关于其在高耸结构风振控制及桥梁振动控制方面都有着较多的应用[3, 4]。例如,徐刚等基于结构一阶模态向单自由度系统简化的方法,进行了施工中桥塔的TMD减振研究[5];Lin等针对结构的一阶弯曲和一阶扭转模态,研究了TMD对大跨度桥梁弯扭耦合抖振响应的减振效果[6]。然而研究发现,TMD对其与结构频率比的变化十分敏感,具有一定频带宽的MTMD可以较好的解决这一问题[7],因而MTMD系统也是振动控制研究中的热点形式之一。Masato和Fujino对MTMD减振系统的动力行为进行了描述,据此提出了MTMD减振设计的相关公式[8]; Kareem等研究了风和地震等随机荷载作用下MTMD的减振性能[9];顾明等以上海杨浦大桥为背景,进行了MTMD用于该桥抖振减振参数研究[10];唐俊华等利用Sap2000进行了常州东经120主题公园景观塔的MTMD风振控制研究[11];白桦等针对主跨246 m杭州之江大桥的拱形钢塔进行了MTMD的风振控制研究[12]。可知,MTMD用于大跨度桥梁主梁、景观塔等结构的抖振控制以及桥塔主塔的涡振控制研究[13, 14]已崭露头角,然而其用于桥塔结构尤其是超大跨度斜拉桥桥塔施工阶段的风致抖振控制研究尚不多见。
苏通大桥桥塔高300.4 m,建成时为斜拉桥中的世界第一高塔,风荷载是施工阶段的主要荷载之一,因此有必要开展减振措施研究,以提升该超高裸塔结构的抗风安全性。本文以该桥为工程背景,基于ANSYS建立了结构三维有限元模型,在对大桥进行结构动力特性分析和桥址区三维脉动风场模拟的基础上,详细探讨了MTMD参数对裸塔结构减振效果的影响规律,分析了其中的关键影响因素,以期为同类型桥塔的抗风减振设计提供参考。
1 工程背景苏通大桥位于江苏省东部南通和苏州市之间,工程全长32.4 km,由跨江大桥和南北接线组成,跨江大桥全长8 146 m,包括主桥、辅桥和南北引桥。大桥按双向六车道高速公路标准设计,设计行车速度100公里每小时。主桥设计采用双塔双索面钢箱梁斜拉桥,全长2 088 m,由7跨组成,桥跨组合为100 m+100 m+300 m+1 088 m+300 m+100 m+100 m,其中主跨跨径为1 088 m,2008年建成通车时为世界跨径最大的斜拉桥,其立面如图 1所示。
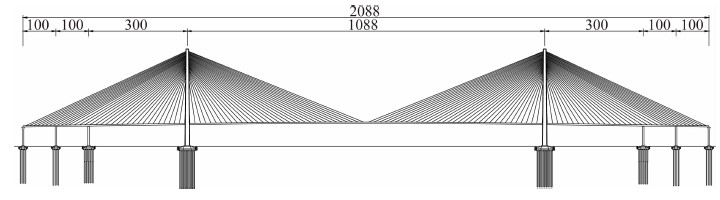 |
| 图 1 苏通大桥立面图Fig. 1 Layout of Sutong Bridge |
苏通大桥桥塔 采用钢筋混凝土结构,塔柱为单箱单室截面A形索塔,如图 2所示。桥塔总高300.4 m,其中上塔柱高91.361 m,中塔柱高155.813 m,下塔 柱高53.226 m,中、下塔柱横桥向外侧面的斜率为1/7.929 5,索塔在桥面以上高度为230.41 m,高跨比为0.212,塔底左右塔柱中心间距62 m。
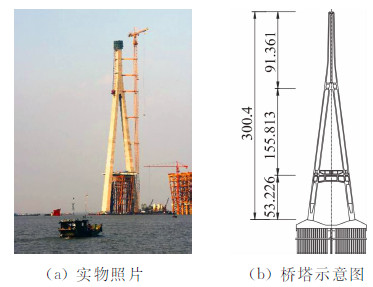 |
| 图 2 施工中的苏通大桥桥塔Fig. 2 Bridge tower of Sutong Bridge under construction |
严格按照苏通大桥设计图纸,基于大型有限元软件ANSYS建立了该桥裸塔结构有限元计算模型,如图 3所示。模型中,塔柱及横梁均采用BEAM4单元进行模拟,单元划分由下横梁位置以及拉索固定位置等共同确定。假定桥塔在承台位置固结,未考虑“土-桩-结构”共同作用。采用子空间迭代法分析了桥塔动力特性,见表 1。
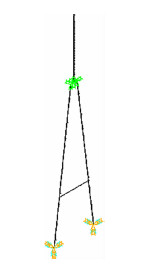 |
| 图 3 苏通大桥桥塔有限元模型Fig. 3 FE model of Sutong Bridge′s tower |
| 阶次 | 频率/Hz | 振型描述 |
| 1 | 0.1504 | 一阶顺桥向弯曲 |
| 2 | 0.4061 | 一阶横桥向弯曲 |
| 3 | 0.6874 | 二阶横桥向弯曲 |
| 4 | 0.7250 | 二阶顺桥向弯曲 |
| 5 | 1.4273 | 三阶横桥向弯曲 |
| 6 | 1.5051 | 一阶扭转 |
上述分析表明,该桥塔结构的振动主要包括顺桥向弯曲、横桥向弯曲和扭转振动三种形式。由于采用了A型桥塔,其顺桥向的刚度明显小于横桥向,因而结构第一阶模态为顺桥向弯曲。
3 三维脉动风场的模拟桥塔为竖向线状结构且竖向脉动风对结构的附着效应较弱,故竖向脉动风速的作用可忽略不计。假设脉动风速为平稳随机过程,采用Davenport相干函数[15]考虑不同空间点脉动风速的相关性,因而桥塔的风场可简化为分别沿顺桥向和横桥向的多个独立的线状一维风速场。风场模拟时,跨中桥面高度处的10 min平均风速考虑了实测[16, 17]和规范两种情况:①凤凰台风过境时,平均风速15.7 m/s;②我国现行规范[18]推荐的百年一遇设计风速38.0 m/s。采用谐波合成法,以Kaimal谱[19]为目标谱,进行了大桥裸塔阶段三维脉动风场模拟,其中考虑了风速相位角的影响。模拟点沿主塔从下而上等间距(30 m)分布,具体参数见表 2。作为代表,图 4给出了USC=15.7 m/s时1、5点模拟的顺风向脉动风速时程。模拟风场的功率谱、相关函数与目标值的对比如图 5、图 6所示。
| 主塔高度 | H=306 m | 模拟点范围 | Z=15~315 m | |
| 主梁高度处 的平均风速 | U SC=15.7 m/s U SJ=38.0 m/s | 地面粗糙长度 | 0.01 m | |
| 脉动风速模拟点数 | n=10 | 截止频率 | ω u=4 π rad/s | |
| 频率分段数 | N=2 048 | 样本时间间隔 | Δ t =0.25 s | |
| 样本周期 | T 0=10 240 s | 采样时段长 | T u=1 200 s | |
| 注:下标“SC”表示实测所得数据,下标“SJ”表示设计数据 | ||||
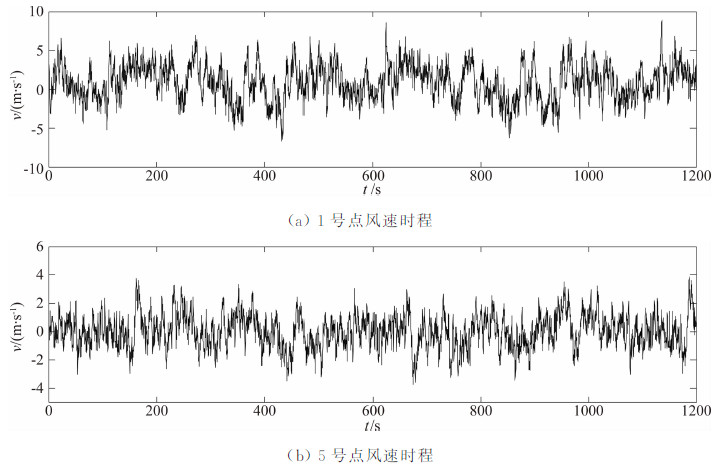 |
| 图 4 顺风向脉动风速时程(USC=15.7 m/s)Fig. 4 Along-wind fluctuating wind speed (USC=15.7 m/s) |
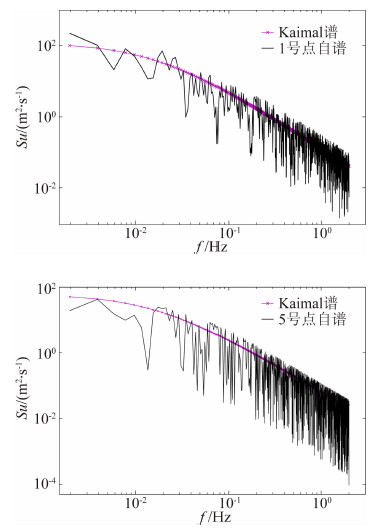 |
| 图 5 模拟风速自谱与目标谱的对比 (USC=15.7 m/s)Fig. 5 Comparison of simulated and target wind speed auto-power spectrum (USC=15.7 m/s) |
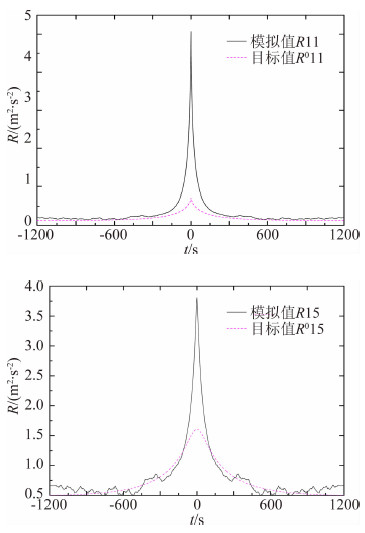 |
| 图 6 模拟风速相关函数与目标值的对比 (USC=15.7 m/s)Fig. 6 Comparison of simulated and target wind speed correlation functions (USC=15.7 m/s) |
由图 5、图 6可知,模拟风速功率谱和相关函数和目标值吻合程度总体上较好,因此,从谱密度和相关性两方检验了模拟风场的可靠性,说明风场模拟结果符合后续风振分析要求。需要指出的是,由于在以上分析中模拟风速样本仅取了1 200 s,且未采用多样本平均技术对模拟风速数据进行处理,使得模拟值与目标值之间存在一定的差别。
4 裸塔MTMD减振分析 4.1 裸塔抖振响应分析基于上述风场模拟结果和有限元计算模型,计算了裸塔阶段在风向角β=0°(横桥向)、β=90°(顺桥向)[2]两种情况下结构的风振响应,塔顶风振响应见表 3。
| 主梁高度处 平均风速 /(m·s -1) | 风向角 β/(°) | 结构响 应方向 | 位移 RMS值 /mm | 位移 峰值 /mm | 加速度 RMS值 /(10 -3m·s -2) | 加速度 峰值 /(10 -3m·s -2) |
| U SC=15.7 | 0 | 顺桥向 | 0.10 | 0.30 | 0.1 | 0.3 |
| 0 | 横桥向 | 1.00 | 3.70 | 5.0 | 18.2 | |
| 90 | 顺桥向 | 5.40 | 17.10 | 4.5 | 13.1 | |
| 90 | 横桥向 | 0.04 | 0.15 | 0.2 | 0.7 | |
| U SJ=38.0 | 0 | 顺桥向 | 0.70 | 2.00 | 0.6 | 2.0 |
| 0 | 横桥向 | 7.30 | 27.80 | 38.4 | 140.0 | |
| 90 | 顺桥向 | 60.10 | 174.60 | 53.3 | 154.0 | |
| 90 | 横桥向 | 0.09 | 0.36 | 0.5 | 1.8 |
为了确保主塔的安全性及施工人员舒适性,通常将结构加速度允许幅值设为0.5 m/s2以下,要求在低风速下进行施工。两种情况下,塔顶顺、横桥向的加速度响应RMS值均不超过0.06 m/s2,峰值不超过0.2 m/s2。可见,该桥塔顶加速度响应满足一般要求。
4.2 MTMD减振参数敏感性分析虽然苏通大桥桥塔施工阶段可满足抗风要求,但在设计风速下的抖振加速度峰值已达0.154 m/s2;而随着未来更大跨径桥梁的兴建,桥塔高度也将越来越高,同时近年来强台风愈演愈烈,桥塔抖振响应必将更为突出,因此有必要进行超高桥塔施工阶段减振控制的深入研究。由表 3可见,由于桥塔顺桥向刚度相对于横桥向较小,β=90°时塔顶顺桥向位移相对较大。因此,以塔顶顺桥向位移为控制目标,进行桥塔的风振控制研究。
研究表明,高耸结构各方向的一阶振型一般对其相应方向的风振响应贡献最大,其余振型贡献较小,可忽略不计。因此,将桥塔的一阶顺桥向弯曲振型确定为受控振型。以桥塔顶部的位移响应为减振控制目标,定义减振率如下:
式中,D0、D1分别为无控和受控结构的位移响应RMS值。δ越大表明减振效果越好。由于ANSYS并未直接给出各种阻尼器单元,故采用Combin14和Mass21两种单元组合以模拟TMD的质量、刚度和阻尼特性[20]。MTMD布置在桥塔顶部平台位置,在此基础上进行了有控与无控结构的风振响应分析。
4.2.1 TMD数量对减振效果的影响MTMD沿横桥向对称等间距布置在桥塔顶端,其中心频率与结构第1阶振型频率(一阶顺桥向弯曲,f=0.155 4 Hz)调谐,相应的结构模态质量M1=9 080 t。暂取MTMD的质量比μ=0.01,频带宽ΔR=0.1,阻尼比ξ=0.02,TMD数量n=2、3、5、7、9、11时,塔顶位移减振率的变化规律如图 7所示。
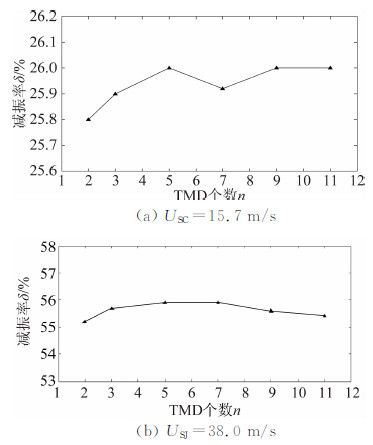 |
| 图 7 TMD数量对减振效果的影响Fig. 7 Influence of the number of TMD on damping effect |
由图 7可知:当MTMD总质量一定时,此时增加TMD数量无益于提高减振效果,但增加TMD数量可使TMD频率分布变密,靠近主控频率的质量增加,可在一定程度上增强MTMD的鲁棒性[10]。两种风速下减振率变化范围分别为25.8%~26.0%和55.2%~55.9%,该MTMD系统在风速较大时,减振效果更加明显。对于本桥塔,考虑TMD质量块体积及安装空间的要求,n=3比较合理。图 7还表明,本案例中高风速下MTMD的控制效果更佳,其可能原因是风与桥梁结构气动耦合效应的影响,使得MTMD装置的频率更加接近于高风速下风-桥梁耦合系统的振动频率。
4.2.2 质量比对减振效果的影响取n=3,暂取MTMD的频带宽ΔR=0.1,阻尼比ξ=0.02,MTMD总质量比μ=0.005、0.01、0.015、0.02、0.025、0.03时,塔顶位移减振率的变化规律如图 8所示。
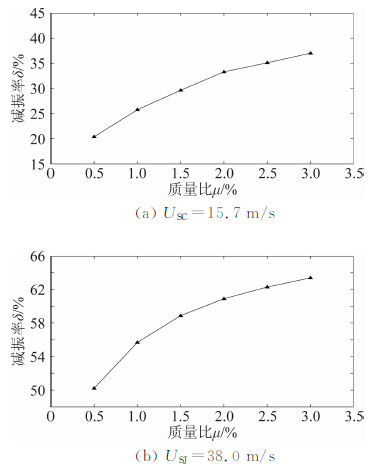 |
| 图 8 质量比对减振效果的影响Fig. 8 Influence of mass ratio on damping effect |
由图 8可知:MTMD的质量比对减振效果影响显著,质量比越大,减振效果越好。但减振效果的趋势渐趋平缓,说明当质量比增大到一定程度后,减振 率增加的幅度有限。考虑桥塔顶部平台使用空间要 求,本桥塔取质量比μ=2%较为合理,此时单个TMD质量块重约60.5 t,若采用铁块(ρ≈7 800 kg/m3),则尺寸约为1.98 m×1.98 m×1.98 m,满足使用空间要求,同时质量比取2%可以保证两种风速下的有效减振率。研究还发现,当ΔR、ξ变化时,MTMD质量比对减振率的影响规律大致相同,在此不再赘述。
4.2.3 频带宽对减振效果的影响取n=3,μ=2%,暂取阻尼比ξ=0.02,MTMD频带宽ΔR=0.05、0.1、0.15、0.2、0.25、0.3、0.35、0.4时,塔顶位移减振率的变化规律如图 9所示。
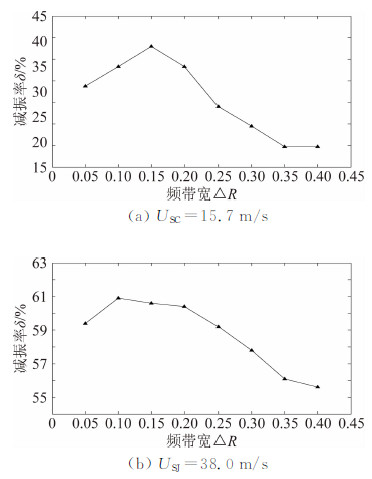 |
| 图 9 频带宽对减振效果的影响Fig. 9 Influence of bandwidth on damping effect |
由图 9可知:当n、μ和ξ一定时,随着ΔR的增加,减振率先增后减。实测和设计风速对应的最佳频带宽分别为ΔRSC=0.15和ΔRSJ=0.10。必须指出,实际工程中MTMD的ΔR应考虑以上情况进行综合确定,本文为对比不同风速下的减振效果而采用不同的ΔR值。
4.2.4 阻尼比对减振效果的影响取n=3,μ=2%,频带宽ΔRSC=0.15、ΔRSJ=0.10,MTMD阻尼比ξ=0.005、0.01、0.02、0.03、0.04、0.05、0.06、0.07、0.08时,塔顶位移减振率的变化规律如图 10所示。
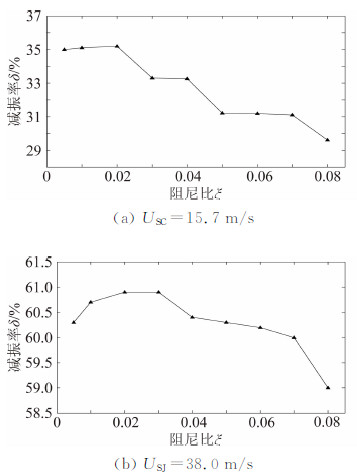 |
| 图 10 阻尼比对减振效果的影响Fig. 10 Influence of damping ratio on damping effect |
图 10 表明:ξ对减振效果影响较小,当ξ小于0.02时,减振率随ξ的增加略有增加,随后则呈下降趋势。因为较大的阻尼会增加结构耗能,同时也会减弱TMD质量块的振动幅度而削弱其减振能力。对于两种风速,裸塔结 构均在ξ=0.02时达到最优减振率。
4.3 MTMD减振效果分析通过以上分析,确定了该桥裸塔阶段减振分析中的MTMD参数,见表 4。此时,USC=15.7 m/s和USJ=38.0 m/s时的减振率分别为35.2%和60.9%。以USC=15.7 m/s为例,制振前后的塔顶顺桥向位移时程如图 11所示;峰值最大的TMD位移时程如图 12所示。
| 工况 | TMD 序号 | 质量 M T/t | 刚度常数 K T/(kN·m -1) | 阻尼常数 C T/(kN·s·m -1) |
| U SC=15.7m/s | 1 | 60.5 | 46.3 | 2.12 |
| 2 | 60.5 | 54.0 | 2.29 | |
| 3 | 60.5 | 62.4 | 2.46 | |
| U SJ=38.0m/s | 1 | 60.5 | 48.8 | 2.18 |
| 2 | 60.5 | 54.0 | 2.29 | |
| 3 | 60.5 | 59.5 | 2.40 |
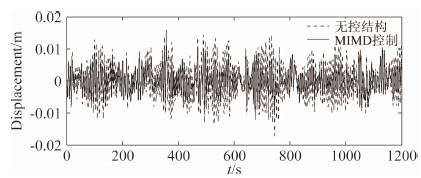 |
| 图 11 桥塔制振前后塔顶的位移时程Fig. 11 Displacement time history at the top of the bridge tower before and after using MTMD |
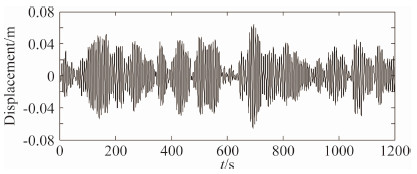 |
| 图 12 TMD的位移时程Fig. 12 Displacement time history of TMD |
以上分析表明,MTMD的设置可有效控制裸塔阶段桥塔顶部的顺桥向位移,且桥塔顶部平台使用空间可满足TMD的最大位移行程要求。对制振前后获得的塔顶位移时程进行傅里叶变换,获得了塔顶位移响应功率谱密度如图 13所示。
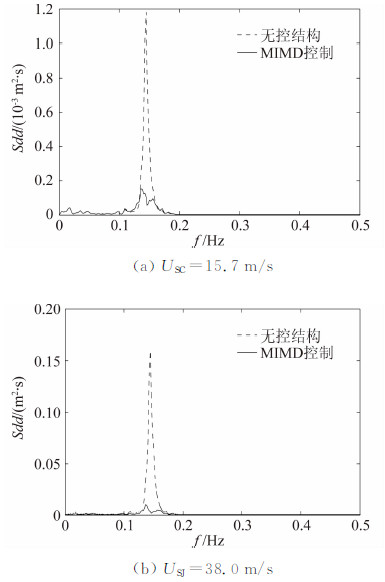 |
| 图 13 制振前后塔顶位移功率谱密度Fig. 13 Power spectral density of bridge tower displacement before and after using MTMD |
图 13可知,塔顶位移功率谱密度的峰值位置对应结构的一阶顺桥向弯曲模态,验证了本文所选取受控振型的正确性。风速较大时,塔顶位移响应谱值远大于低风速情况,表明高风速时桥塔所蕴含的振动能量比低风速情况要大得多。设置MTMD后,两种工况下塔顶位移响应谱均显著降低,证明塔顶位移响应得到了有效控制。
5 结论本文根据规范推荐的桥址区风谱模型,采用谐波合成法模拟了苏通大桥裸塔结构的脉动风场,基于ANSYS平台进行了该桥裸塔结构MTMD减振控制研究,获得了MTMD关键参数的变化对裸塔结构减振效果的影响规律,所得结论具体如下:
(1) 由于桥塔横桥向刚度比顺桥向大得多,所以裸塔阶段桥塔顶部顺桥向抖振位移响应相对突出。而桥塔结构的第一阶顺桥向弯曲模态对桥塔抖振顺桥向抖振位移贡献最大,故结构的振动控制需选其为受控振型。
(2) MTMD的力学参数中,TMD的数量、MTMD的质量比、频带宽、阻尼比等参数的变化对裸塔结构减振效果的影响不尽一致。其中,当MTMD的总质量一定时,TMD的数量对结构减振效果影响不大;MTMD的减振效果随着质量比的增加而增加,随着频带宽或阻尼比的增加先增大后减小。
(3) 通过控制变量法进行MTMD参数敏感性分析,综合考虑桥塔结构的使用空间要求,可获得MTMD在不同风速下的最优力学参数,实现裸塔结构振动的有效控制。就本案例而言,两种风速下的减振率均较高,风速较大时减振效果更优。
必须指出,合理设置MTMD参数可有效降低裸塔结构的抖振位移,但实际应用中MTMD系统参数应综合考虑产品型号、减振效果、经济性、设计及施工等方面予以确定。
| [1] | 项海帆, 葛耀君, 朱乐东, 等. 现代桥梁抗风理论与实践[M]. 北京:人民交通出版社, 2005. |
| [2] | Zhu Ledong, Cao Yinhong, Ding Quanshun, et al. Buffeting performance of the free-standing tower of long-span cable-stayed bridge under yawed wind[J]. Journal of Tongji University(Natural Science), 2005, 33(7):880-884. (in Chinese)朱乐东, 曹映泓, 丁泉顺, 等. 斜风作用下大跨度斜拉桥裸塔抖振性能[J]. 同济大学学报(自然科学版), 2005, 33(7):880-884. |
| [3] | 欧进萍. 结构振动控制——主动、半主动和智能控制[M]. 北京:科学出版社, 2003. |
| [4] | 瞿伟廉. 高层建筑和高耸结构的风振控制设计[M]. 武汉:武汉测绘科技大学出版社, 1991. |
| [5] | Xu Gang, Wang Jingfu, Ren Wenmin, et al. Reduction of vibration during construction of bridge towers by TMD[J]. Engineering Mechanics, 2003, 20(6):106-109. (in Chinese)徐刚, 王靖夫, 任文敏, 等. 施工中大桥桥塔的TMD减振研究[J]. 工程力学, 2003, 20(6):106-109. |
| [6] | Lin Y Y, Cheng C M, Lee C H. A tuned mass damper for suppressing the coupled flexural and torsional buffeting response of long-span bridges[J]. Engineering Structures, 2000, 22:1195-1204. |
| [7] | Igusa T, Xu K. Vibration control using multiple tuned mass dampers[J]. Journal of Sound and Vibration, 1994, 175(4):491-503. |
| [8] | Masato A, Fujino Y. Dynamic characterization of multiple tuned mass dampers and some design formulas[J]. Earthquake Engineering & Structural Dynamics, 1994, 23(8):813-835 |
| [9] | Kareem A, Kline S. Performance of multiple mass dampers under random loading[J]. Journal of Structural Engineering, 1995, 121(2):348-361. |
| [10] | Gu M, Cheng S R, Chang C C. Parametric study on multiple tuned mass dampers for buffeting control of Yangpu Bridge[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89:987-1000. |
| [11] | Tang Junhua, Liu Weiqing, Wang Shuguang, et al. Study on control of wind induced vibration of Changzhou E120 Theme Park Landscape Tower with MTMD[J]. China Civil Engineering Journal, 2010, 43:243-248. (in Chinese)唐俊华, 刘伟庆, 王曙光, 等. 常州东经120主题公园景观塔MTMD风振控制研究[J]. 土木工程学报, 2010, 43(增刊):243-248. |
| [12] | Bai Hua, Li Yu, Li Jiawu, et al. Study on MTMD control of wind-induced vibration for arch steel tower of cable-stayed bridge[J]. China Railway Science, 2013, 34(1):22-28. (in Chinese)白桦, 李宇, 李家武, 等. 斜拉桥拱形钢塔的MTMD风振控制研究[J]. 中国铁道科学, 2013, 34(1):22-28. |
| [13] | Wang Zhongwen, Zhu Hongping, Liao Haili, et al. Vortex-induced vibration reduction of steel free-standing tower using tuned liquid damper[J]. Journal of Huazhong University of Science and Technology, 2009, 26(2):9-11. (in Chinese)王中文, 朱宏平, 廖海黎, 等. 钢桥塔裸塔状态涡激振动的TLD减振方案研究[J]. 华中科技大学学报(城市科学版), 2009, 26(2):9-11. |
| [14] | Wen Yongkui, Sun Limin. Parametric study on vibration control scheme for steel tower of large span cable-stayed bridge[J]. Journal of Tongji University (Natural Science), 2006, 34(3):296-301. (in Chinese)文永奎, 孙利民. 大跨度斜拉桥钢塔制振方案与参数分析[J]. 同济大学学报(自然科学版), 2006, 34(3):296-301. |
| [15] | Simiu E, Scanlan R H. Wind effects on structures:fundamentals and applications to design[M]. John Wiley & Sons, INC, 1996. |
| [16] | Wang Hao, Li Aiqun, Xie Yishun. Field measurement on buffeting response of Runyang Suspension Bridge under typhoon Matsa[J]. ACTA Aerodynamica Sinica, 2008, 26(3):297-303. 王浩, 李爱群, 谢以顺. 台风"麦莎"作用下润扬悬索桥抖振响应实测研究[J]. 空气动力学学报, 2008, 26(3):297-303. |
| [17] | Xie Yishun, Li Aiqun, Wang Hao. Comparison study on experimental strong wind characteristics of Runyang Suspension Bridge[J]. Acta Aerodynamica Sinica, 2009, 27(1):47-51. 谢以顺, 李爱群, 王浩. 润扬悬索桥桥址区实测强风特性的对比研究[J]. 空气动力学学报, 2009, 27(1):47-51. |
| [18] | 中交公路规划设计研究院. JTG/T D60-01-2004公路桥梁抗风设计规范[S]. 北京:人民交通出版社, 2004. |
| [19] | Kaimal J C. Spectral characteristics of surface layer turbulence[J]. Journal of the Royal Meteorological Society, 1972, 98(1):563-589. |
| [20] | Long Xiaohong, Li Li, Tang Jiaxiang, et al. A study on the nonlinear seismic response and TMD control of cable-stayed bridge of the third Aodang Bridge in Macao[J]. China Civil Engineering Journal, 2004, 37(11):56-61. (in Chinese)龙晓鸿, 李黎, 唐家祥, 等. 澳凼第三大桥斜拉桥的非线性地震反应及TMD初步控制研究[J]. 土木工程学报, 2004, 37(11):56-61. |




