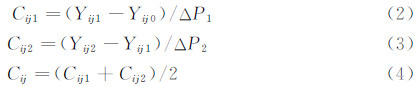0 引言
静气动弹性(简称静弹性)是飞行器在空气动力作用下产生弹性变形而引起其气动特性变化的一种现象。静弹性对飞行器气动特性有较大影响,主要表现为:改变飞行器的几何外形从而改变原有气动载荷;影响飞行器的舵面效率及操稳特性;可能导致升力面发散,出现翼面破坏[1, 2]。例如,一些大飞机在飞行中翼尖的变形可达4~6m的量级,波音707飞机在3km高度亚声速飞行时,静弹性可使飞机气动焦点前移0.06cA(即机翼平均气动弦长的6%),航向静稳定性导数Cnβ下降50%;具有小展弦比机翼的战斗机的气动特性也受到静弹性的显著影响,具有切尖三角翼的某歼击机,在10km高度作两倍声速飞行时,静弹性造成气动焦点前移0.07cA,使Cnβ下降近40%[1]。
通过理论计算或静弹性模型风洞试验可以获得飞行器的静弹性特性,从而精确预测飞行器的的气动特性,保证飞行器的飞行安全。国内静弹性领域的研究人员在飞行器静弹性理论计算方面开展了广泛的研究工作[3, 4, 5, 6, 7],由于静弹性模型高速风洞试验较为复杂,国内关于静弹性模型高速风洞试验方面的研究工作比较少,而国外进行了较多的静弹性模型高速风洞试验研究。俄罗斯中央空气流体动力研究院在Т-109、Т-128风洞对多种飞机开展了静弹性模型高速风洞试验研究,研究了副翼反效、发散、静弹性对载荷分布及气动力影响等问题;美国航空航天局兰利研究中心在TDT风洞进行了F/A-18A飞机静弹性模型高速风洞试验,研究了静弹性对升力线斜率、气动焦点位置、舵面效率等气动特性的影响,测量了舵面的形变,进行了前缘控制面发散预测[8, 9, 10] 。
通过本项静弹性模型高速风洞试验研究,获得了静弹性对升力线斜率、气动焦点位置、襟副翼效率等气动特性的影响及静弹性机翼的弯/扭应变、变形特性,为静弹性模型刚度试验、弯/扭应变信号测量、模型变形视频测量(VMD)及风洞总压控制等静弹性风洞试验能力的提高积累了经验,促进了高速风洞静弹性试验技术的发展。
1 模型与试验设备 1.1 模型静弹性模型与真实飞行器需要满足几何外形相似和刚度相似,根据相似理论,刚度比例尺为:
其中,kEI、kGJ、kl分别为模型与真实飞行器的弯曲刚度比、扭转刚度比、长度比,kq为模型风洞试验速压与真实飞行器的飞行速压比。本项研究中的静弹性试验模型共4个,编号分别为为1#、2#、3#和4#。1#和2#静弹性模型为翼身组合体测力模型,其外形相同,刚度基本一致,由刚性机身与静弹性机翼组成。静弹性机翼采用双梁结构,梁架与蒙皮由复合材料增强玻璃纤维加工而成。模型全长约3m,展长约1.2m,机翼展长0.825m,机翼根弦长0.835m。图 1为1#和2#静弹性模型外形及测压剖面、应变贴片剖面位置示意图。
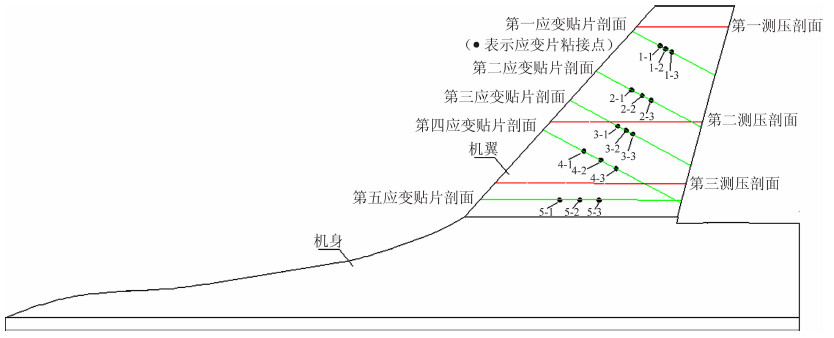 |
| 图 1 1#和2#静弹性试验模型Fig. 1 1# and 2# static aeroelastic testing models |
3#和4#静弹性模型为单独机翼测力模型,其平面形状相同,翼型略有差异,4#静弹性模型刚度较3#静弹性模型增大。静弹性机翼采用外双梁内三梁结构,梁架与蒙皮由复合材料碳纤维加工而成。机翼展长1.383m,机翼根弦长0.579m。图 2为3#和4#静弹性模型内部结构布置图[11]。
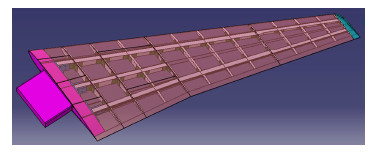 |
| 图 2 3#和4#静弹性试验模型内部结构Fig. 2 Internal structure of 3# and 4# static aeroelastic testing models |
FL-26风洞系试验段横截面为2.4m×2.4m的半回流、暂冲引射式跨声速增压风洞,能够进行变速压试验,试验Ma数为0.3~1.2。风洞试验时,模型通过侧壁转窗支撑于FL-26风洞半模试验段侧壁上。
采用气动中心高速所五分量半模电阻应变天平测量模型的气动力和力矩,采用电子扫描阀测量模型表面压力。
2 试验方法 2.1 刚度试验刚度试验用于测定模型在静态载荷下的结构变形特性[12, 13, 14, 15]。
采用“定点加载,多点测量”的方法对静弹性模型进行挠度影响系数C ij(j表示为第j个加载点,i表示第i个变形测量点)测量,从而检查静弹性模型与真实飞行器的刚度相似程度。测量方法如下:
(1) 未加载时,测量模型各变形测点的坐标Yij0。
(2) 对第一变形测点对应的模型下表面点施加上一个方向垂直向上的载荷ΔP1,测量各变形测点的坐标Yij1;再施加上一个方向垂直向上的载荷ΔP2,测量各变形测点的坐标Yij2。
(3) 更换加载点,重复步骤(2)。当所有变形测点对应的模型下表面点加载完毕,测量完成。
对各加载点加载两次,得到两个挠度影响系数值,然后取其平均,数据处理方法如下:
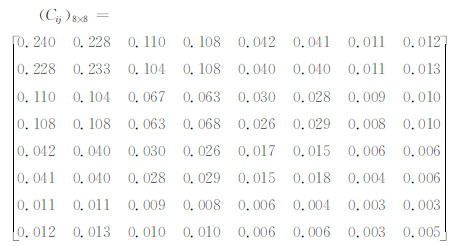
下面给出了测得的3#静弹性试验模型挠度影响系数矩阵[Cij],Cij的单位为10-1mm/N,柔度测量点分布示意图见图 3。
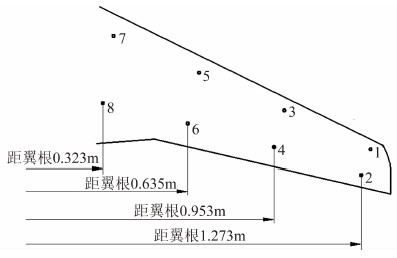 |
| 图 3 3#静弹性试验模型柔度测量点分布示意图Fig. 3 Schematic of flexibility measurement points distribution of 3# static aeroelastic testing model |
对1#和2#静弹性模型进行了气动力、表面压力分布、弯/扭应变信号测量及变速压试验,对1#和2#静弹性模型外形相同的刚模进行了气动力、表面压力分布测量对比试验;对3#静弹性模型及外形相同的刚模进行了气动力测量试验;对4#静弹性模型进行了气动力测量及变速压试验,未进行外形相同刚模对比试验;此外,采用模型变形视频测量(VMD)技术[4, 9]对3#和4#静弹性模型外翼进行了变形测量。模型的测力、测压方法按常规方式进行,下面只简要介绍静弹性模型试验对风洞控制系统的要求、弯/扭应变信号测量方法及弯/扭变形测量方法。
2.2.1 静弹性模型试验对风洞控制系统的要求由于静弹性机翼模型模拟了真实机翼的刚度,其结构强度明显弱于金属模型,而风洞启动、关车过程冲击载荷较大,为了避免静弹性机翼模型在试验过程被损坏,要求进行静弹性模型试验时,风洞启动、关车过程的速压变化平滑、不能出现大的波动。由于静弹性模型的气动特性受速压影响,进行静弹性模型试验时,在流场稳定阶段,要求总压控制精度高。
2.2.2 静弹性模型弯、扭应变测量弹性模型内部应变片组桥电路为半桥电路,采用精密电阻与模型内部的应变片组成应变测量电路,弯、扭应变信号由4芯屏蔽电缆传输,采用信号调理板、多功能数据采集卡、零槽控制器测量应变信号。
2.2.3 静弹性模型弯、扭变形测量在试验模型的上表面布置标记点,用两台高分 辨率摄像机在风洞试验段顶部的观测窗口拍摄试验图像,利用双目立体视觉的原理,测量试验模型上标记点的三维坐标值,再通过对比试验前后标记点的三维坐标位置来计算试验模型机翼在 气动载荷下的变形量。3#静弹性试验模型VMD标记点分布如图 4所示。
 |
| 图 4 3#静弹性试验模型VMD标记点分布Fig. 4 VMD targets distribution of 3# static aeroelastic testing model |
由表 1可知,1#、2#和3#静弹性模型较刚性模是在气动载荷作用下,静弹性机翼模型前缘扭转变形当地迎角增大而后缘扭转变形当地迎角减小所致。
| Ma | 速压(kPa) | 模型 | 静弹性模型与刚性模型升力线斜率比值 | 静弹性模型与刚性模型气动焦点位置差量 |
| 0.60 | 21.8 | 1# | 0.96 | -1.7%c A |
| 0.60 | 21.8 | 2# | 0.96 | -2.8%c A |
| 0.85 | 41.0 | 2# | 0.97 | -2.7%c A |
| 1.14 | 57.0 | 2# | 0.89 | -5.6%c A |
| 0.74 | 34.6 | 3# | 0.99 | -1.0%c A |
| 0.80 | 38.2 | 3# | 0.96 | -3.2%c A |
表 2给出了2#静弹性模型、刚性模型的襟副翼效率对比结果。模型的襟副翼位于机翼后缘内侧。襟副翼效率是在襟副翼偏角δ=0°~-5°范围内获得,2#静弹性模型襟副翼效率较刚性模型明显下降。表 2中,Clδ、Cmδ分别为滚转力矩系数、俯仰力矩系数对襟副翼偏角的导数。
| Ma | 速压/kPa | 迎角/(°) | 2 #静弹性模型与刚性模型襟副翼效率C lδ比值 | 2 #静弹性模型与刚性模型襟副翼效率C mδ比值 |
| 0.60 | 21.8 | 0 | 0.71 | 0.77 |
| 0.85 | 41.0 | 0 | 0.68 | 0.73 |
由表 3和表 4可知,在本项试验研究的速压变化范围内,速压对1#、2#和4#静弹性模型的升力线斜率及气动焦点位置影响较小。
| 模型 | 速压30 kPa、21.8 kPa升力线斜率比值 | 速压30 kPa 、21.8 kPa气动焦点位置差量 |
| 1 # | 0.98 | -0.8%c A |
| 2 # | 0.97 | -0.5%c A |
| 速压49.0 kPa、34.6 kPa升力线斜率比值 | 速压63.0 kPa、49.0 kPa升力线斜率比值 | 速压49.0 kPa、34.6 kPa气动焦点位置差量 | 速压63.0 kPa、49.0 kPa气动焦点位置差量 |
| 0.99 | 1.0 | -0.7%c A | 0.1%c A |
上述试验结果符合静弹性模型气动特性变化规律。静弹性后掠机翼的弯曲、扭转变形使有效迎角变小[16],且随着迎角增大,有效迎角减小幅度愈大,这是产生静弹性模型较刚性模型升力线斜率下降的原因;在正升力作用下,与刚性机翼相比,静弹性机翼前、后缘均出现绕刚轴上翘变形现象,从而导致静弹性机翼前缘的载荷增加、后缘的载荷减小,静弹性模型较刚性模型气动焦点前移;负偏度的襟副翼引起的负升力使静弹性机翼产生抬头方向的扭转,这样,静弹性模型负偏度襟副翼引起的升力和滚转力矩增量都较刚性模型减小,此外,由于气动载荷作用,弹性襟副翼偏度量值会较刚性襟副翼减小,因此,静弹性模型襟副翼效率较刚性模型明显下降。
3.2 静弹性对模型表面压力分布的影响图 5给出了2#静弹性机翼模型、刚性机翼模型表面压力对比曲线。由于静弹性机翼模型变形较大,静弹性机翼模型与刚性机翼模型表面压力差异明显。
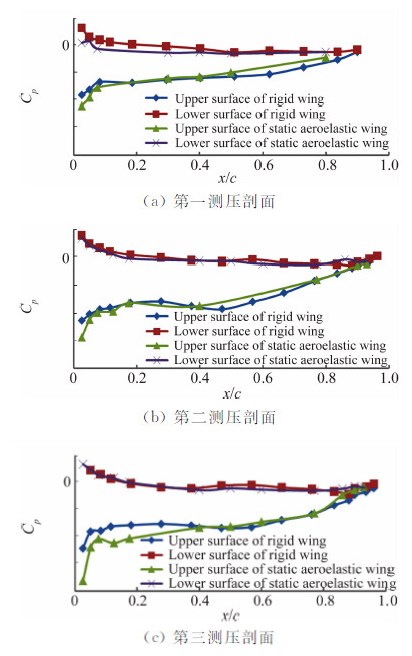 |
| 图 5 2#静弹性机翼模型与2#刚性机翼模型压力分布对比 (Ma=0.6,α=2°,q=21.8 kPa)Fig. 5 Comparison of section pressure for 2# static aeroelastic and rigid wing models (Ma=0.6,α=2°,q=21.8 kPa) |
在Ma=0.6、迎角α=2°、速压q=21.8 kPa时,2#静弹性机翼模型前缘的上表面压力低于刚性机翼模型,后缘的上表面压力高于刚性机翼模型,这可能是在气动载荷作用下,静弹性机翼模型前缘扭转变形当地迎角增大而后缘扭转变形当地迎角减小所致。
3.3 静弹性模型弯、扭应变测量结果静弹性机翼模型弯、扭应变测量旨在获得静弹性机翼模型的弯、扭应变分布,弯、扭应变测量结果可用于分析模型载荷特性[8]。在风洞试验前,按以下方法进行弯、扭应变标定:对静弹性机翼模型下表面各加载点进行单点加载,获得各加载点单位载荷作用下静弹性机翼模型15个应变片贴片点的弯、扭应变信号即应变测量电桥输出的电压信号。图 6给出了风洞试验静弹性机翼模型弯、扭应变信号测量结果,弯、扭应变信号随迎角增加基本呈线性变化,与升力系数、俯仰力矩系数在小迎角范围内随迎角增加基本呈线性变化的规律一致。
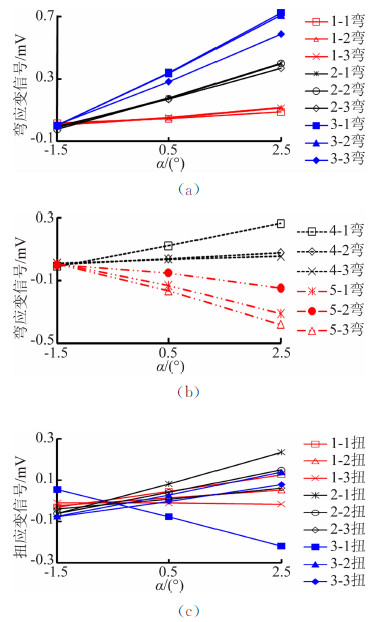 |
| 图 6 弯/扭应变信号随迎角的变化曲线 (Ma=0.6,q=21.8 kPa)Fig. 6 Bending and torsion strain signals versus angles of attack (Ma=0.6,q=21.8 kPa) |
3#静弹性试验模型6个变形测量弦向剖面距翼根距离分别为0.692 m、0.791 m、0.892 m、0.992 m、1.093 m、1.193 m。图 7给出了3#静弹性试验模型6个弦向剖面50%当地弦长位置的弯曲变形测量结果。图 8给出了3#静弹性试验模型6个弦向剖面的扭转变形测量结果(对于大展弦比机翼,假定弦向剖面是绝对刚硬的[16])。3#静弹性试验模型为大展弦比后掠机翼,在正迎角时,模型上翘弯曲变形,剖面气动弹性扭转变形角为负值(使有效迎角减小),剖面越靠近翼尖弯、扭变形越大;在Ma=0.8、α>2°时,剖面弯、扭变形随迎角增加增幅减小,这是由于翼面绕流出现分离从而升力系数随迎角增加增幅减小所致(如图 9所示)。
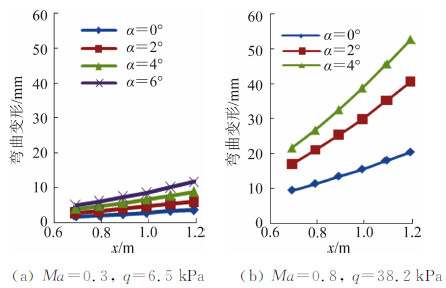 |
| 图 7 3#静弹性试验模型弯曲变形测量结果Fig. 7 Blending deformation measurement results of 3# static aeroelastic testing model |
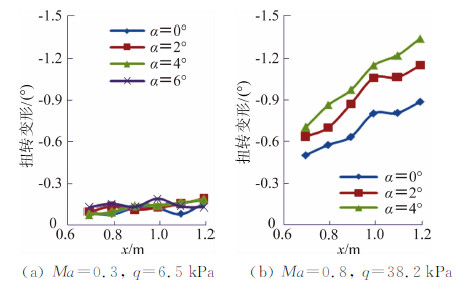 |
| 图 8 3#静弹性试验模型扭转变形测量结果Fig. 8 Torsional deformation measurement results of 3# static aeroelastic testing model |
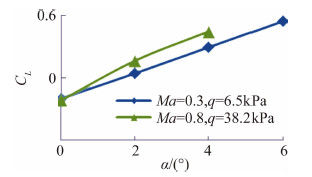 |
| 图 9 3#静弹性试验模型升力系数随迎角的变化曲线Fig. 9 Lift coefficient versus angles of attack for 3# static aeroelastic testing model |
通过本项研究,得出以下结论:
(1) 静弹性翼身组合体和单独机翼模型较刚性模型均出现了升力线斜率下降、气动焦点前移现象,2#静弹性模型襟副翼效率较刚性模型明显下降。在本项试验研究的速压变化范围内,速压对1#、2#和4#静弹性模型的升力线斜率及气动焦点位置影响较小。
(2) 2#静弹性模型与刚性模型表面压力差异明显。在Ma=0.6、迎角α=2°、速压q=21.8kPa时,2#静弹性机翼模型前缘的上表面压力低于刚性机翼模型,后缘的上表面压力高于刚性机翼模型。
(3) 在小迎角范围内,静弹性机翼模型弯、扭应变信号随迎角增加基本呈线性变化。
(4) 在正迎角时,大展弦比后掠机翼静弹性模型的剖面扭转变形使有效迎角减小,剖面越靠近翼尖弯、扭变形越大。
本项研究中的模型刚度试验、测力、测压、弯/扭应变信号测量、模型变形视频测量(VMD)及风洞总压控制等试验技术成熟,为飞行器静弹性研究提供了良好的试验平台。
| [1] | Wang Faxiang, et al. High speed wind tunnel testing[M]. Beijing:National Defense Industry Press, 2003. (in Chinese)王发祥, 等. 高速风洞试验[M]. 北京:国防工业出版社, 2003. |
| [2] | Yun Qilin. Experiments in aerodynamics[M]. Beijing:National Defense Industry Press, 1991. (in Chinese)恽起麟. 实验空气动力学[M]. 北京:国防工业出版社, 1991. |
| [3] | Zheng Chengxing, Xiao Xiaoling. The exploration of elastic aerodynamics for a joined wing configuration[J]. Acta Aerodynamica Sinica, 2005, 23(01):93-96. (in Chinese)郑诚行, 肖小玲. 翼尖连接机翼布局弹性气动力探讨[J]. 空气动力学学报, 2005, 23(01):93-96. |
| [4] | Zhang Shujun, Wang Yuntao, Meng Dehong. Study on static aeroelasticity for high aspect ratio joined-wings[J]. Acta Aerodynamica Sinica, 2013, 31(02):170-174. (in Chinese)张书俊, 王运涛, 孟德虹. 大展弦比联接翼静气动弹性研究[J]. 空气动力学学报, 2013, 31(02):170-174. |
| [5] | Chen Dawei, Yang Guowei. Static aeroelastic analysis of a flying-wing using different models[J]. Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(04):469-479. (in Chinese)陈大伟, 杨国伟. 静气动弹性计算方法研究[J]. 力学学报, 2009, 41(04):469-479. |
| [6] | Xiong Juntao, Qiao Zhide, Yang Xudong.An aerodynamic shape optimization of transonic wing design method for aeroelastic system[J]. Acta Aerodynamica Sinica, 2009, 27(02):154-159. (in Chinese)熊俊涛, 乔志德, 杨旭东. 一种计及静气动弹性变形影响的跨声速机翼气动优化设计方法研究[J]. 空气动力学学报, 2009, 27(02):154-159. |
| [7] | Sun Yan, Zhang Zhengyu, Deng Xiaogang. Static aeroelastic effects of wind tunnel model on aerodynamic forces[J]. Acta Aerodynamica Sinica, 2013, 31(03):294-300. (in Chinese)孙岩, 张征宇, 邓小刚. 风洞模型静弹性变形对气动力影响研究[J]. 空气动力学学报, 2013, 31(03):294-300 |
| [8] | Heeg J, Spain C V, Fiorance J R, et al. Experimental results from the active aeroelastic wing wind tunnel test program[R]. AIAA 2005-2234. |
| [9] | Spain C V, Heeg J, Ivanco T G, et al. Assessing videogrammetry for static aeroelastic testing of a wind-tunnel model[R]. AIAA 2004-1677. |
| [10] | Ivanco T G, Heeg J, Rivera Jr J A. An investigation of leading edge control surface divergence and its experimental prediction[R]. AIAA 2003-1960. |
| [11] | Kou Xiping. Research on high speed static aeroelastic model design of high-aspect-ratio wing[D].[Master's Thesis]. Mianyang:China Aerodynamics Research & Development Center, 2013. (in Chinese)寇西平. 大展弦比机翼高速静气动弹性模型设计研究[D].[硕士学位论文]. 绵阳:中国空气动力研究与发展中心, 2013. |
| [12] | Guan De. Aeroelastic experiment[M]. Beijing Aeronautics College Press, 1986. (in Chinese)管德. 气动弹性试验[M]. 北京:北京航空学院出版社, 1986. |
| [13] | Lizotte A M, Lokos W A. Deflection-based aircraft structural loads estimation with comparision to flight[R]. AIAA 2005-2016. |
| [14] | Northington J S, Pasiliao C. F-16 wing structural deflection testing-phase I[R]. AIAA 2007-1674. |
| [15] | Pendleton E, Flick P, Paul D, et al. The X-53 a summary of the active aeroelastic wing flight research program[R]. AIAA 2007-1855. |
| [16] | Chen Guibin, Zou Congqing, Yang Chao. Aeroelastic design foundation[M]. Beijing:Beijing University of Aeronautics and Astronautics Press, 2004. (in Chinese)陈桂彬, 邹丛青, 杨超. 气动弹性设计基础[M]. 北京:北京航空航天大学出版社, 2004. |