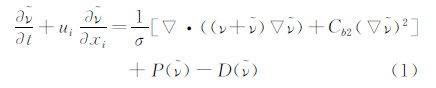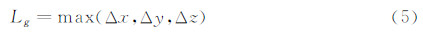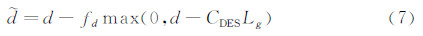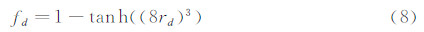2. University of Southampton, Southampton UK SO17 1BJ
2. University of Southampton, Aerodynamics and Flight Mechanics Group, Southampton, SO17 1BJ, UK
0 引 言
随着战斗机和无人机的内埋弹舱的应用,腔体结构的气动噪声问题成为研究热点。腔体的声学共振现象[12]产生于腔体前缘剪切层的不稳定增长,振荡的高速气流撞击到腔体后壁产生压强波形成声源,压强波向前传播并与前缘剪切层进行能量交换增强了自由剪切层的不稳定性,将在腔体后缘再次引发强烈的气流撞击,从而形成周期性的反馈回路[3]。当反馈压强波的频率与相位同自由剪切层一致时会导致共振[4]。腔体的这种自持振荡引发的气动噪声量级高达170 dB,会产生声疲劳和声辐射,造成结构破坏和舱内电子仪器失灵[5]。
国外关于开式腔体的气动噪声分析从1966年Rossiter[6]进行方形腔体噪声试验和半经验公式开始到现在已经发展十分成熟,现阶段主要研究重点在腔体结构的噪声抑制方法上,主要包括扰流棒[7, 8]、前缘扰流片[9]、质量喷流[10]等方法。国内从1996年罗柏华等[11]开始关注腔体噪声问题,现阶段研究主要关于噪声机理和计算方法。司海清、王同光[12]等对空腔振荡频率估算方程进行了改进,郝宗瑞[13]、马明生[14]和宋文萍等对空腔噪声的计算做了研究。噪声控制方法研究尚属起步阶段,张林[15]、罗新福[16]、杨党国[17]、范召林等采用试验的方法研究了腔体振荡影响因素以及质量喷流和后壁倾角等控制手段对腔体振荡的抑制效果。国外关于前缘扰流片的噪声控制方法研究已经成熟并被广泛应用在F-22和F-111[18]等飞机上,但国内关于前缘扰流片等被动控制方法的研究成果较少。
为了使简单有效的扰流片被动控制方法应用于国内内埋弹舱设计中,本文基于DDES的CFD方法来对安装有前缘锯齿形扰流片的腔体进行流场分析和声学计算,以验证这种被动控制方法对腔体气动噪声的抑制效果,并与试验数据进行了对比。
1 DDES方法单方程Spalart-Allmaras(S-A)[19]湍流模型可表示为:
耗散项表示为:
源项定义为:
其中,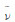 为湍流涡粘变量,ν为分子运动粘性系数,
为湍流涡粘变量,ν为分子运动粘性系数,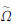 =|Ω|+
=|Ω|+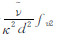 表示为涡量,σ、Cb1、Cb2、κ为常数。fw和fv2方程用来减小物面区域的湍流粘性,d表示流场中某点到最近壁面的距离。
表示为涡量,σ、Cb1、Cb2、κ为常数。fw和fv2方程用来减小物面区域的湍流粘性,d表示流场中某点到最近壁面的距离。
基于S-A单方程湍流模型的混合RANS/LES方法本质上是将方程(2)耗散项中的距离用下式代替:
其中,CDES是常数,常取为0.65。Lg是网格尺度,定义为:
Δx、Δy、Δz为某网格点三个方向上的网格尺寸。因此,当网格在物面附近时,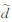 =d,这时流场求解使用基于S-A单方程湍流模型的RANS方法。当网格远离物面时,
=d,这时流场求解使用基于S-A单方程湍流模型的RANS方法。当网格远离物面时,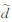 =CDESLg,这时湍流涡粘性系数的衰减便由当地的网格尺寸确定。通过式(1)可知,当源项的湍流涡流性系数与耗散项的衰减达到平衡时,这时的涡粘性系数
=CDESLg,这时湍流涡粘性系数的衰减便由当地的网格尺寸确定。通过式(1)可知,当源项的湍流涡流性系数与耗散项的衰减达到平衡时,这时的涡粘性系数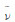 与
与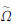 d2成正比关系,此时
d2成正比关系,此时 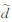 =CDESLg,则有:
=CDESLg,则有:
变成了Smagorinsky[20]亚格子模型。即在远离物面的地方,流场求解表现为LES所需要的亚格子模型。这种混合RANS/LES的方法称为分离涡模拟(Detached Eddy Simulation,DES)[21]方法。
由于在物面附近平行于物面方向的网格尺寸通常大于边界层的厚度,依据式(4)的判定条件可以保证在边界层内使用RANS算法。但是,若物面网格各个方向上都较为细密则可能使LES算法在边界层内被提前启动。这种情况下,边界层内的网格是无法满足LES计算要求的,并且计算效率将会下降。因此,一种称为延迟分离涡模拟(Delayed Detached Eddy Simulation,DDES)的改进DES算法被提出来以保证边界层内完全使用RANS算法[22]。
DDES算法是将式(4)的判据做如下改动:
其中:
rd被视为是当地湍流尺度与距离壁面距离的比值。在远离壁面区域rd«1,使得fd=1,该区域使用LES算法。其它区域中fd=0,使用RANS算法。不难想象,当涡粘度系数从数值较大的区域转向相对较小的区域时,将使得物面边界层附近的DDES模型从LES模式向RANS转变。
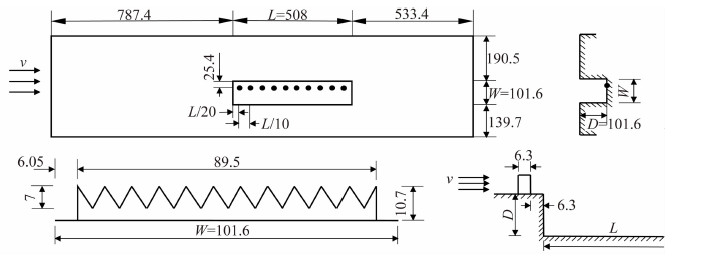
2 试验与计算用来与计算结果做比较的试验由Ross、Foster等[23]于1991年11月在Bedford英国皇家飞机研究院的ARA风洞中进行[24]。试验腔体长深比L/D=5,宽深比W/D=1。腔体模型的底部均布了10个Kulite压强传感器来测量腔体内部的非定常压强变化。试验的采样频率为6 kHz,时长3.2 s。试验台、腔体与扰流片的尺寸与结构如图 1所示。
|
| 图 1 试验腔体与计算扰流片尺寸(mm) Fig. 1 Cavity and spoiler model (unit: mm) |
计算模型是基于实验台基本尺寸向上延伸10倍腔体深度。上边界和流动方向的前后边界采用压强远场边界条件,两侧边界采用对称条件,下边界为无滑移的壁面。来流马赫数Ma=0.85,压强P=62 940 Pa,温度T=270.25 K,涡粘比μt/μ0=10。为了准确捕捉到产生声源的涡结构,腔体内部以及开口剪切层位置处网格布置十分细密,第一层网格y+值控制在2左右,计算网格总数为在450万左右。腔体与扰流片计算网格如图 2所示。

|
| 图 2 计算腔体与扰流片网格 Fig. 2 Mesh for cavity and spoiler |
计算基于Fluent计算平台,采用二阶隐式时间积分的格心有限体积法,无粘通量采用Roe-FDS的通量差分分裂格式,粘性通量采用三阶MUSCL空间离散格式。计算时间步长为10-5s,每步进行30次迭代计算,总计算时间持续了1s。在进行瞬态计算之前首先进行基于S-A单方程模型的稳态计算直到流场收敛,前0.5s时间的瞬态计算舍去,最后0.5s的流场信息以100 kHz的采样频率做声学分析。
计算在英国University of Southampton的Iridis3服务器上进行,采用36个4核2.27 GHz的处理器来进行腔体流场瞬态计算。空腔和带扰流片腔体均在30 000步以上的稳态计算后开始瞬态计算,空腔工况用时55天,带扰流片腔体用时57天完成。
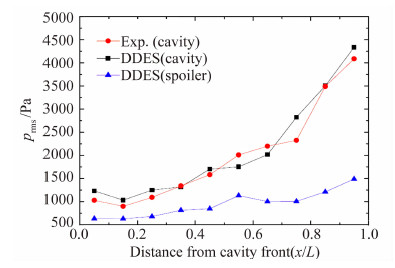
3 结果与分析图 3给出了DDES计算空腔结果与试验结果的对比,以及计算得到的安装有扰流片的腔体底面10个压力测量点的压强均方根值。
|
| 图 3 腔底压强均方根结果比较 Fig. 3 Comparison of experimentand DDES on prms |
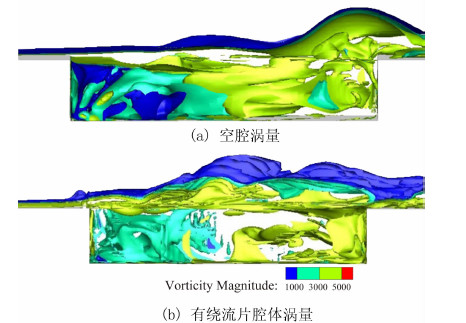
腔底压强的波动是腔体自激振荡的现象,如前文所介绍,剪切层撞击腔体后壁面使得腔体后部的涡严重振荡导致压强变化剧烈,如图 3所示。通过与试验进行对比,本文所用的DDES方法很好的计算出了空腔底部压强的振荡变化规律。安装前缘锯齿形扰流片的DDES结果表明腔体内部的压强波动得到了较大的抑制。其抑制机理是前缘扰流片可以将剪切层向上抬离腔体上方,如图 4(b)所示,使得剪切层在后缘撞击腔体后壁的强度和进入腔体的流量大为降低。高速气流流过锯齿形扰流片产生许多小尺度的涡结构,这些涡结构向后传播起到了稳定剪切层缓解其振荡幅度的作用,这使得扰流片能有效地降低腔体内部的压强脉动水平。
|
| 图 4 空腔(上)和装有扰流片腔体(下)涡量图 Fig. 4 Vorticity magnitudes of clean cavity (up) and cavity with spoiler (down) |
腔体流动的频域分析方法可以给出压强脉动的模态特征。使用声压级的指标对腔底不同位置进行分析。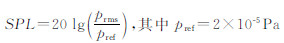 是国
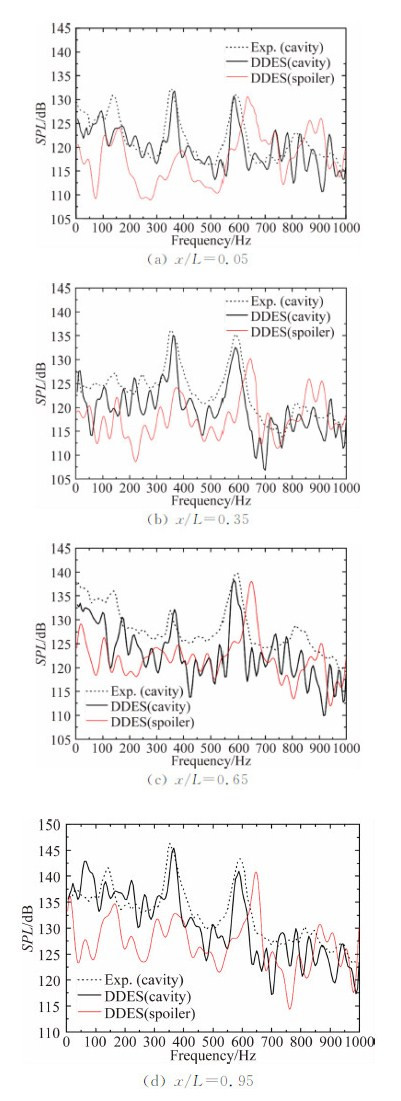
际公认的人耳可听声压阈值。图 5显示了腔体底面从前到后部四个典型测压点位置声压级变化的空腔
试验和计算结果以及带有扰流片的DDES结果。
是国
际公认的人耳可听声压阈值。图 5显示了腔体底面从前到后部四个典型测压点位置声压级变化的空腔
试验和计算结果以及带有扰流片的DDES结果。
|
| 图 5 x/L=0.05、0.35、0.65、0.95位置的声压级 Fig. 5 SPL at x/L=0.05,0.35,0.65,0.95 |
通过声谱图可以看出腔体后部的噪声等级显著高于腔体前部,声压级谱中的第二阶与第三阶模态较为显著的成为主导模态。计算结果对于第二阶和第三阶主导模态的预测与试验结果吻合较好,高频段的预测值出现多点峰值,这与Xiaoxian Chen等[25]的结果是一致的。第四阶模态的具体位置并不是很清晰,但是幅值与试验值差距较小。第一阶模态在腔体前部位置的预测同样也不是很清晰,而在腔体后部噪声等级较大时被清晰的预测出来。通过在腔体前缘添加锯齿形扰流片的控制手段后,计算结果表明腔体内部的全局噪声等级总体上有了明显的下降,尤其是对于前两阶声压级模态的抑制效果显著,对于第二阶主导模态幅值的降低达到10 dB以上。本文分析的锯齿形扰流片装置对声压级的第三阶主导模态的抑制效果微弱,但是改变了该模态的发生频率。
通过Rossiter[15]关于腔体振荡模态的半经验公式的预测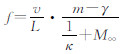 ,其中m和v分别表示模态数和自由来流速度,常数γ=0.25,κ=0.57分别表示相位延迟、平均扰动对流速度与自由来流的比值。分析腔体最后部的测压点x/L=0.95位置处的各阶模态频率与幅值,如表 1所示。
,其中m和v分别表示模态数和自由来流速度,常数γ=0.25,κ=0.57分别表示相位延迟、平均扰动对流速度与自由来流的比值。分析腔体最后部的测压点x/L=0.95位置处的各阶模态频率与幅值,如表 1所示。
| Mode | 1st | 2nd | 3rd | 4th | |
| Rossiter Fomulation | Frequency/Hz | 159 | 371 | 582 | 794 |
| Experiment (clean cavity) | Frequency/Hz Amplitude/dB | 142 141.6 | 353 146.3 | 592 143.4 | 813 130.2 |
| DDES (clean cavity) | Frequency/Hz Amplitude/dB | 67.5 143.0 | 366.6 145.5 | 589.0 141.0 | 783.7 130.0 |
| DDES (with spoiler) | Frequency/Hz Amplitude/dB | 164.1 134.7 | 371.2 132.8 | 647.2 140.7 | 866.6 130.6 |
由表 1可知Rossiter公式可以大体预测出各阶模态的 频率位置,与试验值相比前两阶模态发生频率高17 Hz左右,后两阶模态频率低于试验值10~20 Hz,总体上认为误差较小,说明Rossiter半经验公式对于空腔结构声调频率的预测精度较高。DDES预测的各阶频率除了第一阶 模态预测提前外,其余误差不超过4%。关于噪声幅值的预测DDES在所有四阶位置均十分准确,误差均控制在2 dB以内。由于腔体流动呈现较强的非定常特性,为了捕捉剪切层的作用和各种尺度的涡的瞬时特性,需要数量巨大的网格,而且第一阶与第四阶模态的幅值相比于主导模态较小,使得非主导模态的计算准确度不及主导模态。计算安装有扰流片以后通过DDES计算结果可以看出各阶模态的频率位置发生变化。与空腔的试验值和DDES仿真值相比,所有四阶模态频率均向高值移动,前两阶模态增幅为20 Hz左右,后两阶模态增幅为高达50 Hz。原因是由于扰流片的作用,除了将腔口处的剪切层抬升远离腔体外,它可以将大涡打碎成小涡,改变了腔体内部的涡结构,从而改变了由涡碰撞引发的声学共振现象的各阶模态,使得各阶模态发生频率均被增大。而与Rossiter公式预测的频率相比,更大的差异性说明Rossiter公式在仅考虑腔体长度和来流速度的前提下,只适合预测空腔结构而对于带有控制措施的腔体预测结果略差。DDES结果表明扰流片结构在对腔体内部总体声压级水平进行抑制的同时,对前两阶模态的幅值也有较大幅度降低。处于主导地位的第二阶模态在添加扰流片以后被降低了13 dB,第一阶模态被降低了8 dB,降噪效果较为显著。
4 结 论通过对来流Ma数为0.85下的长深宽比为5∶1∶1的 方形空腔和带有前缘扰流片的腔体使用DDES方法进行气动噪声分析后得到如下结论:
(1) 腔体内部声调噪声的产生是由剪切层的不稳定振荡引发,通过剪切层撞击腔体后壁产生向上游传播的压强声波进一步对剪切层干扰从而形成反馈回路。前缘锯齿形扰流片可以有效将高速剪切层抬离腔体上方,并且其产生的小涡具有稳定剪切层的作用,使得腔内后壁的撞击减弱达到抑制噪声幅值的效果。
(2) 延迟分离涡模拟(DDES)方法对于腔体气动噪声分析的仿真结果较为准确。腔体所有模态的声调噪声等级预测结果误差控制在2 dB以内,对于第二三阶主导模态的发生频率误差也控制在4%以内。仿真认为前缘锯齿形扰流片对第二阶主导模态的降噪幅度在10 dB以上,对腔体内部整体声压级降幅在5 dB左右。
本文首次将DDES方法用于腔体气动噪声分析中,准确预测出腔体声调噪声的主导模态。但是对于占非主导地位的第一阶模态发生频率预测误差较大,同时对于第四阶模态的仿真结果出现多个峰值,难以准确确定发生位置。使用前缘锯齿形扰流片的被动控制方法来抑制腔体气动噪声,可以引发对不同形式的扰流片(如平板或圆柱形)的降噪效果进行分析和探讨。
| [1] | Yang Dangguo, Li Jianqiang, Liang Jinmin. Sound generation induced by self-sustained oscillations inside cavities based on CFD and aeroacoustic theory[J]. Acta Aerodynamica Sinica, 2010, 28(6): 724-730. (in Chinese) 杨党国, 李建强, 梁锦敏. 基于CFD和气动声学理论的空腔自激振荡发声机理[J]. 空气动力学学报, 2010, 28(6): 724-730. |
| [2] | VakiliAD, Wolfe R, NaglePA. An experimental investigation of cavity aeroacoustics in high speed flows[R]. Air Force Office of Scientific Research, Aerospace & Materials Sciences Directorate, 1995. |
| [3] | Yang Dangguo, Luo Xinfu, Li Jianqiang, et al. Analysis of aeroacoustic characteristics in open cavities influenced by boundary-layer thickness[J]. Acta Aerodynamica Sinica, 2011, 29 (4): 486-490. (in Chinese) 杨党国, 罗新福, 李建强, 等. 来流边界层厚度对开式空腔气动声学特性的影响分析[J]. 空气动力学学报, 2011, 29 (4): 486-490. |
| [4] | LawsonSJ, BarakosGN. Assessment of passive flow control for transonic cavity flow using detached-eddy simulation[J]. Journal of Aircraft, 2009, 46 (3): 1009-1029. doi: 10. 2514/1.39894 |
| [5] | MortonMH, HampsonCD, AlexanderRA. Final vibration and acoustic loads development for certification of the F-22 advanced tactical fighter[C]. Schaumburg, IL: 49th AIAA/ASME/ASCE/ AHS/ASC Structures, Structural Dynamics, and Materials Conference, 2008. |
| [6] | RossiterJE. Wind-tunnel experiments on the flow over rectangular cavity at subsonic and transonic speeds[R]. London: Ministry of Aviation Aeronautical Research Council, 1966. |
| [7] | Lackey S, TramelRW, LandrumDB. Weapons bay acoustic suppression usinganovel rod in crossflow configuration[C]. 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, 2011. |
| [8] | ThiemannCL, MilneGJ, VakiliAD. An experimental investigation of supersonic cavity flow control with vertical cylinders[C]. 43rd AIAA Fluid Dynamics Conference, 2013. |
| [9] | NicholsRH.Acomparison of hybrid RANS LES turbulence models forageneric weapons bay with and withoutaspoiler[C]. 26th AIAA Applied Aerodynamics Conference, 2008. |
| [10] | Zhuang N, AlviFS, AlkislarMB, et al. Supersonic cavity flows and their control[J]. AIAA Journal, 2006, 44(9): 2118-2128. doi: 10. 2514/1.14879 |
| [11] | Luo Baihua, Hu Zhangwei. Experimental study of flow induced cavity oscillationand its suppression by sound excitation[J]. Journal of Nanjing University of Aeronautics and Astronautics, 1996, 28(3): 331-336. (in Chinese) 罗柏华, 胡章伟. 流动诱导空腔振荡及其声激励抑制的实验研究[J]. 南京航空航天大学学报, 1996, 28(3): 331-336. |
| [12] | Si Haiqing, Wang Tongguang, Zong Huiying. Influence of the plate on the cavity flow-induced oscillationsand the modification of the oscillation frequency equation[J]. Journal of Aerospace Power, 2006, 21(6): 6-11. (in Chinese) 司海青, 王同光, 宗慧英. 腔内平板对空腔自激励振荡的影响及预估振荡频率方程的改进[J]. 航空动力学报, 2006, 21(6): 6-11. |
| [13] | Hao Zongrui, Wang Leqin, Zhou Zhonghai, et al. Numerical simulation of cavity flow field and aeroacoustic[J]. Journal of Zhejiang University (Engineering Science), 2013, 47(1): 131-138. (in Chinese) 郝宗睿, 王乐勤, 周忠海, 等. 空腔流场及气动噪声数值模拟[J]. 浙江大学学报(工学版), 2013, 47(1): 131-138. doi: 10.3785/j.issn.1008-973X.2013.01.019 |
| [14] | Ma Mingsheng, Zhang Peihong, Deng Youqi, et al. Numerical simulation investigation of supersonic cavity flow[J]. Acta Aerodynamica Sinica, 2008, 26 (3): 388-393. (in Chinese) 马明生, 张培红, 邓有奇, 等. 超声速空腔流动数值模拟研[J]. 空气动力学学报, 2008, 26(3): 388-393. |
| [15] | Zhang Lin. Aeroacoustic experimental investigation of the cavity flow fields in high speed wind tunnel[D]. Changsha: National University of Defense Technology, 2006. (in Chinese) 张林. 高速风洞弹舱流场气动声学特性试验研究[D]. 长沙: 国防科技大学, 2006. |
| [16] | Yang Dangguo, Wu Jifei, Luo Xinfu. Investigation on suppression effect of zero-net-mass-flux jet on aerodynamic noise inside open cavities[J]. Acta Aeronauticaet Astronautica Sinica, 2011, 32(6): 1007-1014. (in Chinese) 杨党国, 吴继飞, 罗新福. 零质量射流对开式空腔气动噪声抑制效果分析[J]. 航空学报, 2011, 32(6): 1007-1014. |
| [17] | Yang Dangguo. Studies on aeroacoustic characteristics and noise suppressions for internal weapon bays[D]. Mianyang: China Aerodynamics Research and Development Center, 2010. (in Chinese) 杨党国. 内埋武器舱气动声学特性与噪声抑制研究[D]. 绵阳: 中国空气动力研究与发展中心, 2010. |
| [18] | LeonardLShaw, Rodney Clark, Disk Talmadge. F-111 generic weapons bay acoustic environment[J]. Journal of Aircraft, 1988, 25 (2): 147-153. |
| [19] | Travin A, Shur M, Strelets M, Spalart P. Physical and numerical upgrades in the detached-eddysimulation of complex turbulent flows[M]. Advances in LES of Complex Flows, Kluwer Academic Publishers:PFriedrich, W. Rodi, 2002: 239-254. |
| [20] | Smagorinsky J.General circulation experiments with the primitive equations[J]. Monthly Weather Review, 1963, 91: 99-165. |
| [21] | SpalartPR. Detached eddy simulation[J]. Annual Review of Fluid Mechanics, 2009, 41: 181-202. doi: 10.1146/annurev.fluid.010908.165130 |
| [22] | Rodriquez G, Velez C, Ilie M. Numerical studies of high-speed cavity flows using LES, DDES and IDDES[C]. Grapevine, Texas: 51th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, 2013. |
| [23] | FosterGW, RossJA, AshworthRM. Weapon bay aerodynamics wind tunnel trials and CFD modeling by QinetiQ UK[C]//Proceeding of the RTO/AVT Symposium on Flow-Induced Unsteady Loads and the Impact on Military Applications, Budapest, Hungary: 2005. |
| [24] | HenshawMJ de C. M219 cavity case-verification and validation data for computational unsteady aerodynamics[R]. Rep. RTO-TR-26, AC/323 (AVT) TP/19, QinetiQ, UK: 2000. |
| [25] | Chen Xiaoxian, SandhamND, Zhang Xin. Cavity flow noise predictions[R]. MSTARR DARP, Southampton: 2007. |