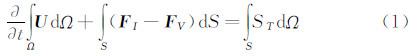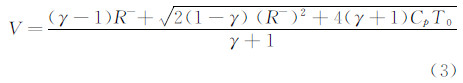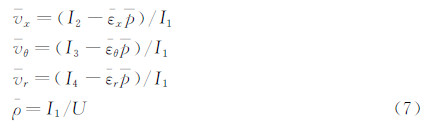0 引 言
航空发动机内部流动十分复杂,对于其可靠性、 寿命及可维护性要求极为苛刻[1],对于军用航空发动 机来说,推重比更是衡量其先进程度的一个重要指 标。为了提高航空发动机的性能,普遍的做法是提 高涡轮的进口温度、增加压缩比、提高压气机和涡轮 的效率[2]。压气机是航空发动机的重要部件,压气机 的气动性能是影响整个发动机的效率、推力和运转性 能的关键因素,因此充分认识压气机内部的流动机 理,准确预测其气动性能对发动机的设计有着重要意 义。
随着高性能计算机的快速发展,计算流体力学 (CFD)技术被越来越多的用于航空发动机压气机的设计和分析,其优点是周期短、成本低、效率高,是传统试验方法很好的互补。压气机CFD模拟的一大难点是如何模拟转/静子叶片排之间相对运动引起的非定常流动。采用滑移面网格[3]进行全流道非定常计算,上下游叶片排之间利用插值进行数据传递,能够捕捉到这些非定常现象,然而缺点是计算量太大。Denton提出的混合平面方法[4]基本思想很简单,转/静界面上下游的通量在相同展向高度处先通过周向平均后再进行传递,将非定常流动简化为准定常问题,从而只需要对一个叶片流道进行计算,大大减小了计算量。虽然这种方法忽略了转/静子相对运动造成的非定常效应,但是依然能够准确模拟压气机的性能和一些流动特性。因此,本文选取混合平面法,在已有的三维流场求解器MFlow的基础上,着力于自主开发压气机内流模拟程序,达到对压气机气动性能的预测能力。相比于商业软件,利用自主开发的程序具有更好的灵活性,能够应对各种不同的复杂问题。本文通过对NASA的两个不同压气机Rotor 67[5]和Stage 35[6]进行计算,并同试验结果进行了对比分析,检验了软件对压气机性能的模拟能力,能够为压气机气动设计提供参考。
1 计算模型 1.1 控制方程压气机内部流场的三维可压缩粘性Navier-Stokes(N-S)方程在旋转直角坐标系(x,y,z)下的形式为:
式中,Ω表示控制体的体积,S表示控制体封闭面的面积,U 为守恒变量,F I为无粘通量,F V为粘性通量,ST为科里奥利力和离心力引起的源项,具体定义参考文献[7]。 1.2 数值方法
对于式(1)的雷诺平均N-S方程采用基于控制体的有限体积方法离散。采用Roe迎风格式[8]计算通过控制体单元面的无粘通量。利用格林-高斯公式计算控制体单元的梯度,选择Venkataknshnan限制器[9]将控制体的原始变量通过线性重构插值到控制体单元面左右,达到更高的空间精度。本文中粘性项采用中心格式计算,时间项利用LU-SGS隐式推进方法[10],并采用局部时间步长加速收敛的技术,提高计算效率。湍流模型选取Spalart-Allmaras(SA)一方程模型[11]。
1.3 边界条件进出口采用特征边界条件。在进口,给定总温 T0,总压P0以及来流速度方向。向进口外发出的黎曼不变量R-由第一个内部边界点外插计算得到,利用R-计算出绝对速度大小V,再根据速度方向将V 分解为各个速度分量[12]:
式中,v d代表边界内部第一个单元速度矢量,cd为当地声速,γ为比热比,n 为法向量,Cp为定压比热。密度ρ和压力p利用T0、P0、V 之间的代数关系以及等熵关系计算得到。
在出口边界,展向高度r处的静压是给定的。虚拟网格的密度和速度分量直接通过外插得到,而当地静压结合式(4)给出的径向平衡方程和给定位置的静压积分得到。
由于利用单个叶片通道的网格进行计算,因此引入了周期边界条件。对于两个周期面上的网格,首先需要根据坐标建立一一对应的关系,在计算时周期边界上的网格类似内部网格,虚拟网格物理量直接通过相对应周期边界的网格得到。
对于粘性物面,采用无滑移边界条件,即相对于物面的速度为零。物面分转动部分和静止部分,对于转子和部分轮毂,有固定的转动速度。物面为绝热壁,物面温度直接由内部点外插得到。
1.4 转/静界面处理对于转/静界面,也是一种特殊的边界条件。本文对转/静界面的处理采用混合平面法,如图 1所示。在混合面处,对上下游变量沿圆周方向( θ 方向)分别进行周向平均,将平均量作为边界条件的值进行传递,在每一步的计算迭代中,上游混合面网格的平均值传递给下游虚拟网格,同理下游混合面网格的平均值传递给上游虚拟网格。最终收敛时,混合面上下游的平均值将趋向一致,达到质量、动量和能量守恒的目的。
 |
| 图 1 混合平面法示意图Fig. 1 Mixing plane method |
对于平均方法的选取,有多种不同的选择,包括面积平均、质量平均等等。本文采用通量平均策略(通常称为Mixed-out Average)[13],以保证质量、动量和能量的守恒。为了求解平均量,首先计算出无粘通量的面积平均,再根据式(5)的关系式反解出构成
这些通量的原始变量。
式中,I代表通量,A代表面积,ε代表单位法向分量,x、θ、r分别代表轴向方向、圆周方向和径向方向,U为速度在法向的投影,e为能量,上标的横线代表是平均量。
式(5)给出了一个关于 的二次方程,其解为:
式中,正号用于亚声速流动。进而通过式(7)迅速得到其他几个平均量:
2 算例与分析 2.1 NASA rotor 67NASA rotor 67是一个跨声速压气机转子叶片,其 在33.25 kg/s的流量下设计压比为1.63,一圈共有22个叶片,设计转速为16 043 r/min,叶尖转速达到429 m/s,叶尖的相对马赫数为1.38。Strazisar和Wood等对这个转子进行过测试,得到了详尽的试验数据[5],Chima等也对rotor 67进行过数值计算[14]。本文首先利用MFlow对这个单独的叶片进行计算,并与试验数据对比,对计算程序的控制方程、边界条件、湍流模型等进行了验证。计算网格采用全六面体网格,忽略了叶尖间隙,总网格量在70万左右,如图 2所示。
 |
| 图 2 Rotor 67叶片和计算网格Fig. 2 Rotor 67 blade and computational grid |
通过调节出口背压 来计算得到不同流量下总压比和绝热效率的工况曲线,并且同试验数据进行对比,如图 3所示,其中对流量除以壅塞流量进行了归一化。试验测得的壅塞流量为34.96 kg/s,而计算得到的壅塞流量为34.68 kg/s,之间相差0.8%。计算得到的失速流量在最大流量的92%左右,与试验相符。计算得到的总压比和绝热效率变化趋势和试验吻合较好,除了在近失速状态时计算的压比要偏低一 些。
 |
| 图 3 Rotor 67总体性能随流量变化Fig. 3 Overall performance of rotor 67 |
图 4给出了最佳效率点附近工况从叶根到叶尖30%和70%两个不同展向位置计算和试验对比的相对马赫数等值线图。在70%位置,叶片前缘处有一道 强的弓形激波,在靠近尾缘附近的流道间有一道强的正激波,激波位置和试验结果一致。在30%位置,叶片吸力面前端形成一块小的超声速区域,和试验结果相似。计算结果验证了本文程序的准确性和可靠性。
 |
| 图 4 不同展向位置相对马赫数分布计算与试验对比Fig. 4 Blade to blade Mach number countors at different span, CFD(left) and experiment(right) |
NASA stage 35是多级跨声速压气机中的其中一级,由转子部分rotor 35和静子部分stator 35组成,其中转子一圈共36个叶片,静子46个叶片。Reid和Moore曾经对stage 35的气动性能进行了测试并给出了详细的数据[6],这些数据为众多CFD软件模拟多级压气机提供了参考。通过对stage 35的计算,进一步验证了程序对“混合平面法”应用的正确性。stage 35的计算网格如图 5所示,转/静子网格块只取一个流道,各自生成,同样周期面网格完全对应,在转子尾缘和静子前缘中间位置上下游网格共面,即“混合平面”。
 |
| 图 5 Stage 35 计算网格示意图Fig. 5 Stage 35 computational grid |
图 6给出了计算得到的在叶高中间位置处压力的等值云图,可以看到在转子前缘处有一道强的弓形激波,在静子叶片15%弦长位置有一道正激波。在上下游的交界面处,当地静压并不连续,这是因为“混合平面”法是在此利用周向平均值进行传递的,仅仅 保证了上下游的平均量的连续性。图 7给出了近失速状态对熵值进行周向平均后在子午面上的分布云图,可以看到在转子叶尖缝隙之后有明显的熵增,这说明叶尖泄流是造成失速工况下流动损失的很大原因。
 |
| 图 6 Stage 35一半叶高位置静压计算结果Fig. 6 Static pressure at mid-span of stage 35 |
 |
| 图 7 周向平均熵值云图Fig. 7 Pitch averaged entropy contours |
图 8给出了stage 35总压比、总温比和绝热效率 计算结果,并同试验数据以及NASA Glenn研究中心的求解器SWIFT[15]的计算结果进行了对比。总体来说,CFD计算的结果和试验比较一致,对比MFlow 和SWIFT的结果,MFlow在某些流量工况下压比和温比数值要偏低一些。
 |
| 图 8 Stage 35整体性能计算结果和试验对比Fig. 8 Overall performance of stage 35, pressure ratio, temperature ratio and effiency |
图 9给出了最大效率状态和近失速状态rotor 35的性能展向分布,计算结果和试验比较一致。可以看出在40%展向位置以下有一个低的总压区域,即总压变化有呈“亏损”趋势,造成这个现象的原因是“角区失速”。本文的计算结果同样捕捉到了这个现象。但是总压并没有呈现出试验那样偏低得非常明显,分析其原因很可能是因为计算时忽略了静子的轮毂和转子之间的间隙泄流导致的。
 |
| 图 9 Stage 35最佳效率(PE, Peak Efficiency)状态和近失速(NS, Near Stall)状态出口展向性能分布Fig. 9 Spanwise profiles of exit at peak effiency(PE, Peak Efficiency) state and near stall(NS, Near Stall) state |
本文采用了基于周向平均的混合面法,对航空发动机压气机转/静子相对运动进行了模拟,使得复杂的非定常计算简化为准定常计算,大大减小了计算量。虽然由于方法的局限性导致在混合面处无法保证物理量的连续性,但是不影响一些关键气动性能参数的计算,具有较好的工程应用价值。通过和试验数据的对比,验证了本文程序的适用性和可靠性,可以为压气机设计进行气动性能预测。但是,在某些方面模拟精度仍存在不足,例如在靠近轮毂附近的总压亏损,计算得到的总压沿展向分布的曲线在这一区域虽然也有减弱的趋势,但远没有试验结果明显。因此,计算格式、湍流模型、网格等因素对计算结果的影响还需要在今后工作中进一步研究。
| [1] | Zhou Sheng, Han Zhenxue, Meng Qingguo. Some applications of computational fluid dynamics in the field of air-breathing propulsion[J]. Acta Aerodynamica Sinica, 1998, 16(1): 97-107. (in Chinese) 周盛, 韩振学, 孟庆国. 计算流体力学在吸气式推进领域中的某些应用[J]. 空气动力学学报, 1998, 16(1): 97-107. |
| [2] | Li Jianfeng, Lyu Junfu. Performance study of technology of combustion inside turbine using in fanjet[J]. Acta Aerodynamica Sinica, 2010, 28(3) : 356-362. (in Chinese)李建锋, 吕俊复. 涡轮燃烧技术在涡扇航空发动机上的应用分析[J]. 空气动力学学报, 2010, 28(3): 356-362. |
| [3] | Rai M. Three-dimensional Navier-Stokes simulations of turbine rotor-stator interaction. I-Methodology[J]. AIAA Journal of Propulsion and Power, 1989, 5(3): 305-311. |
| [4] | Denton J D. The calculation of 3-D viscous flow through multistage turbomachines[J]. Journal of Turbomachinery, 1992, 114: 18-26. |
| [5] | Strazisar A J, Wood J R, Hathaway M D, et al. Laser anemometer measurements in a transonic axial flow fan rotor[R]. NASA TP-2879, 1989. |
| [6] | Reid L, Moore R D. Performance of a single-stage axial-flow transonic compressor with rotor and stator aspect ratios of 1.19 and 1.26, respectively, and with design pressure ratio of 1.82[R]. NASA TP-1338, 1978. |
| [7] | Chen J P, Ghosh A R, Sreenivas K, et al. Comparison of computations using Navier-Stokes equations in rotating and fixed coordinates for flow through turbo machinery[R]. AIAA-97-0878, 1997. |
| [8] | Luo H, Baum J D, Lohner R. An improved finite volume scheme for compressible flows on unstructured grids[R]. AIAA-95-0348, 1995. |
| [9] | Venkatakrishnan V. On the accuracy of limiters and convergence to steady state solutions[R]. AIAA-93-0880, 1993. |
| [10] | Rieger H, Jameson A. Solution of steady 3-D compressible Euler and Navier-Stokes equations by an implicit L U scheme[R]. AIAA-88-0619, 1988. |
| [11] | Spalart P R, Allmaras S R. A one equation turbulence model for aerodynamic flows[R]. AIAA-92-0439, 1992. |
| [12] | Chima R V. Viscous Three-dimensional calculations of transonic fan performance[R]. NASA TM-103800, 1991. |
| [13] | Chima R V. Calculation of multistage turbomachinery using steady characteristic boundary conditions[R]. NASA TM-206613, 1998. |
| [14] | Chima R V. Viscous three-dimensional calculations of transonic fan performance[R]. NASA TM-103800, 1991. |
| [15] | Chima R V. SWIFT code assessment for two similar transonic compressors[R]. NASA TM-2009-215520, 2009. |