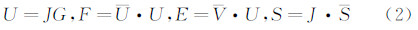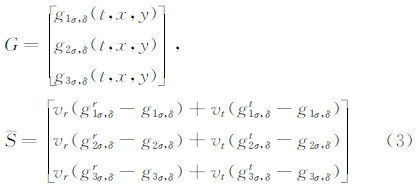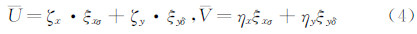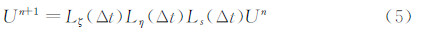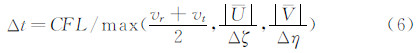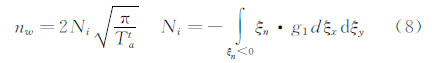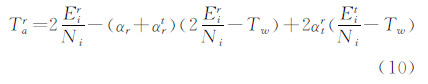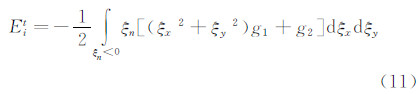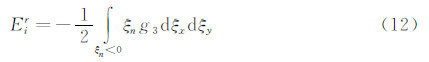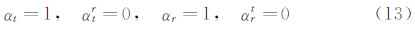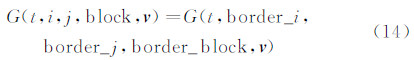0 引 言
气体的宏观流动本质上是由分子的微观运动决 定的,而描述微观层次的基本方程是基于分子量子力 学系统的Liouville方程及基于约化s粒子分布函数 的BBGKY方程链,二者是等价的[1]。仅考虑二体碰撞,并作混沌假设得到Boltzmann方程[2],它采用速度分布函数描述一个微观体系的平均行为,严格意义上来说它属于介观层次的分子运动描述。其中速度分布函数f是空间位置r和速度v的连续平滑函数,它并不包含每个微观分子的细致结构[1]。开展气体动理学研究一般都是基于Boltzmann方程,并且经过学者不断发展得到了多原子气体、多组元混合气体及化学反应混合气体的分子输运Boltzmann方程[1, 3]。但由于它是一个高维多重积分的微分方程,且非线性碰撞项极其复杂,直接求解是很困难的[3, 4]。比较广泛采用的方法包括Chapmann-Enskog逐级逼近解法[4]、模型方程方法[5]、有限差分Monte Carlo方法[6]及格子Boltzmann方法[7]。
最近十几年以来,针对Boltzmann方程开展的研究工作再次成为国际上的热点问题,基于模型方程的数值求解方法取得了极大进步。徐昆等发展了气体运动BGK格式(GKS)求解高速粘性流动等问题[8],为连续、近连续流动模拟提供了一种新的思路。李志辉发展离散速度坐标法求解Boltzmann模型方程[9],在平板Couette流动[10]等问题中得到应用,并建立起基于HPF、MPI的并行算法用于三维绕流[11, 12]。在解决实际问题中,为了模拟复杂物形绕流或多体流场,需要在位置空间建立能描述整个流场特性的网格系统。非结构网格虽然对复杂外形适应能力很强,但其计算效率相对较低[13],技术处理和相应算法改进上难度较大。相比较而言,分区对接网格对于气体运动论统一算法中的位置空间有限差分方法来说更容易实现。而且这种网格技术的对接面两侧网格点完全对接,避免了虚网格及流场信息的代数插值,既保证了对复杂外形的适应能力,又能较好地保证流动通量守恒[14]。
本文采用分块对接网格系统处理二维复杂外形或多体流动问题,针对气体运动论统一算法在速度空间的速度离散、位置空间的有限差分进行算法设计和技术处理,得到能够描述多体干扰流动问题的跨流域算法程序,并验证对接面两侧流场参数是否光滑过渡。
1 计算方法 1.1 控制方程考虑转动非平衡效应的二维Boltzmann-Rykov模型方程[15]无量纲形式[16]在速度空间离散成为各个离散速度坐标点上彼此独立的若干方程组,并将位置空间坐标通过雅克比(Jacobian)矩阵变换到计算平面内,得到二维跨流域气体运动论统一算法的控制方程形式为[17]:
其中,σ=1,2,…,N1;δ=1,2,…,N2。g1、g2、g3是约化速度分布函数[17],它是关于时间t,位置空间r和速度空间v的多维函数(对于二维问题具有五个自变量)。vt、vr 分别是弹性碰撞频率和非弹性碰撞频率。
采用非定常时间分裂方法[9],将控制方程(1)分裂为源项碰撞变化方程和位置空间的对流运动方程,得到求解约化速度分布函数方程的气体运动论数值格式为:
其中,下标 s表示源项,ζ、η 为计算平面坐标。
时间上采用二阶Runge-Kutta推进,位置空间采用NND-4(a)有限差分格式[18]。则该有限差分数值计算方法的稳定性条件为[19]:
其中,CFL为时间步长调节系数,一般CFL<1。 1.2 物面边界条件
考虑转动非平衡效应气体运动论统一算法的物面边界条件由分子与物面碰撞通量守恒无穿透条件[20]和平动、转动能量平衡关系得到[21]:
其中,气体分子经物面反射的数密度 nw 可确定为:
在物体表面,气体的平动温度 Tat和转动温度Tar 可表示为:
公式(9)、(10)中的适应系数 αt、αtr、αr和αrt 采用完全热适应边界条件[21]:
2 分区对接网格算法分区对接网格技术及其算法是数值模拟真实复杂流动的有效途径。在分区流动计算中涉及两个关键技术:一是边界类型及分区相邻关系判断;二是邻近分区之间信息的交换及流动信息在整个求解域中的传播。
由于流场采用固定网格划分,网格不随时间演变,因此在统一算法迭代之前的初始化过程中通过分区之间的位置关系判断邻近分区编号。判断区域单元的每个边界类型,如果是分区对接面则还需要给出邻近分区内该对接面的网格序列号。
控制方程在每个分区中是独立求解的,因此保证对接面两侧流场信息的正确传递是算法成功的关键。为了保证流场光滑过渡及流场信息在整个求解域内的正确传递,每个分区对接面网格的有限差分格式精度应该与内点保持一致,这就需要在对接面外设置虚拟网格,虚拟网格点的信息通过相邻分区同一位置的值给出。值得注意的是分布函数G=G(t,r,v )是关于速度 v 的函数,因此虚拟网格点上速度方向在邻近分区内对应的速度方向必须保持一致。虚拟网格点上的分布函数值可写为:
其中border_i、border_j表示相邻块内该位置的网格点编号。
为了保证流场信息在分区对接面上的光滑过渡,需要对两侧分区分别迭代得到对接面上的分布函数值进行平均操作。物面和来流边界的处理与单域网格一致[17]。
3 算例与讨论 3.1 竖直平板绕流算例验证文献[16]开展了稀薄过渡流区二维竖直平板高马赫数绕流计算,本文以其为算例验证分区对接网格的气体运动论统一算法程序可靠性。计算区域及网格分区如图 1所示,竖直平板厚度不计,高为1。左端自由来流氮气的无量纲速度[17]为S∞=7.0,壁面温度Tw=10,努森数Kn∞=0.01。图 2给出了数值计算得到该高马赫数竖直平板流场的无量纲压力等值线分布,可以看到左端来流在平板前端形成一道脱体激波。各网格分区之间的流场参数实现了光滑过渡,说明对接面处理方法是合理的。流场信息在全求解域内实现了较好地传递。
 |
| 图 1 竖直平板流场网格分区Fig. 1 Multi-block patched mesh for flow past a erect plate |
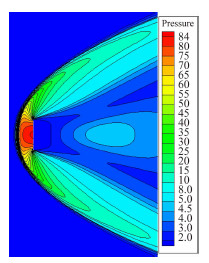 |
| 图 2 平板绕流压力等值线Fig. 2 Pressure contours of plate flow |
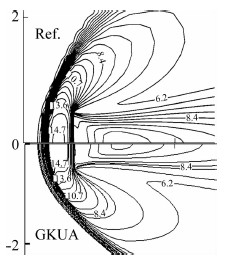
图 3中基于分区对接网格的气体运动论统一算法(GKUA)计算得到流场平动温度分布与文献[16]基本一致,包括脱体激波位置和形状、等值线分布变 化趋势等。比较结果表明本文的分区对接网格实现是可靠的。此外,GKUA得到的流场等值线更加光滑,不会出现波浪式起伏现象,这是分区对接网格相比于单域网格的一大优势。图 4中平板前端流场减速线上(y=0)的无量纲密度、平动温度、转动温度分布与文献的比较也很好地说明了分区对接网格在气体运动论统一算法中实现过程的可靠性。
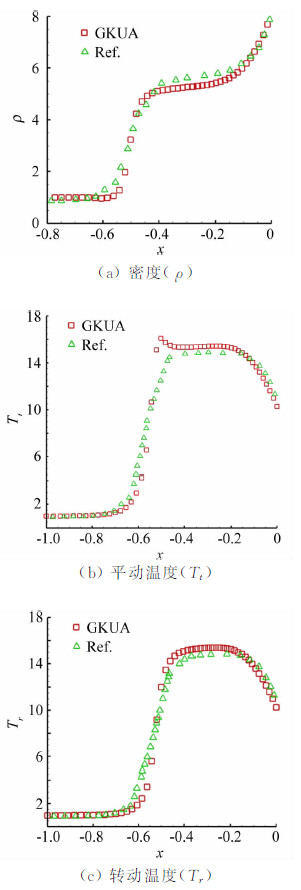 |
| 图 4 平板前端减速线上的流动参数分布Fig. 4 Macro-parameter distribution on forepart decelerating line |
将0.01 m×0.04 m的二维简化Crookes辐射计模型置于0.44 m×0.44 m的方腔内,辐射计风向标左侧温度为450 K、右侧为410 K,方腔壁温固定为300 K。模型及流场分区网格如图 5所示。由于辐射计左右两侧以及方腔壁之间的温差导致气体对流运动。图 6给出了统一算法采用分区对接网格(图 5)计算得到该辐射计流场温度分布与DSMC方法数值模拟结果的比较情况,可以看出二者能够较好地在上下交界处匹配起来,尤其是近壁区域能完全重合。图中DSMC方法的结果存在统计波动现象,而基于分区对接网格的统一算法(GKUA)等值线分布则较为光滑细腻,凸显出后者在计算这种低速辐射对流问题方面的优越性。
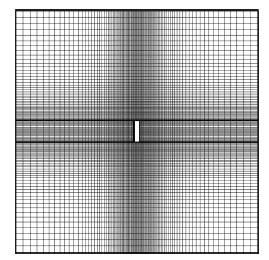 |
| 图 5 Crookes辐射计模型及分区网格Fig. 5 Model and multi-block patched mesh for Crookes vane |
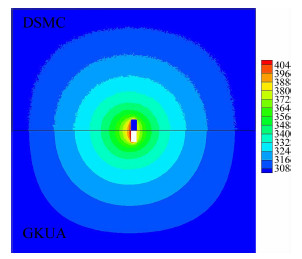 |
| 图 6 Crookes辐射计流场的温度分布Fig. 6 Temperature distribution around the vane |
图 7、图 8分别给出辐射计左侧中心线、上半部分中心垂直线上的无量纲温度和密度分布比较。可以看出DSMC和统一算法(GKUA)的计算结果沿这 两条线的流场参数轮廓线完全重合,进一步验证了分区对接网格在统一算法中的实现是可靠的。
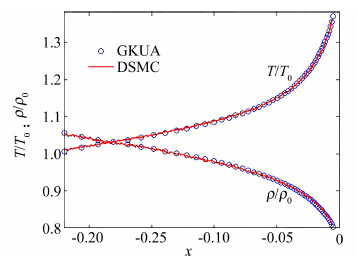 |
| 图 7 辐射计左侧中心线上的温度与密度分布Fig. 7 Temperature and density distribution along the central line at the left side of the vane |
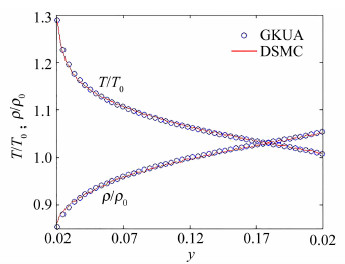 |
| 图 8 辐射计上侧中心垂直线上的温度与密度分布Fig. 8 Temperature and density distribution along the central vertical line above the vane |
流场中存在多个物体的情况需要采用分区对接网格才能描述。本文以相互交错放置的两个长方形为算例开展高马赫数(Ma∞=6)多体流场计算。来流克努森数为Kn∞= 0.003 65( 对应近连续流区),来流温度T∞=273.15 K,设置壁面温度为Tw=300 K,流动气体为单原子氩气Ar。图 9给出了两个长方形的相对位置及流场网格划分,其中长方形无量纲宽度为1,长度为5,左右交错1,上下距离为2。
 |
| 图 9 两个长方形流场网格Fig. 9 Mesh system for flow with two rectangles |
图 10-图 12是该多体干扰流场的马赫数、无量纲温度和压力等值线云图。可以看到整个流场在各网格分区之间光滑过渡,流场特征明显且合理,证明分区对接网格在气体运动论统一算法中的实现是正确的,分区对接面的处理是合理有效的。该多体干扰流场表现出连续流区的流动特征:物体前端出现脱体激波,使得超声速来流跨越激波成为亚声速流动。波后是高温高压区,延续到两个交错长方形的位置,最大无量纲温度和压力值分别达到13.5和55。脱体激波的形状不规则,下方要“胖”一些。
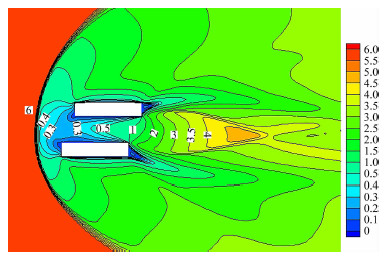 |
| 图 10 两个长方形流场马赫数等值线云图Fig. 10 Mach number contours for flow with two rectangles |
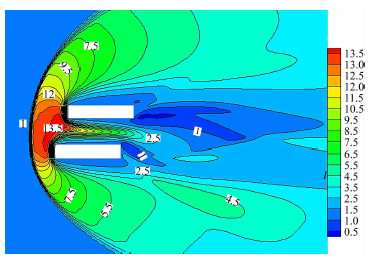 |
| 图 11 两个长方形流场温度等值线云图Fig. 11 Temperature contours for flow with two rectangles |
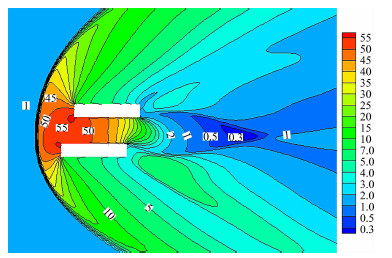 |
| 图 12 两个长方形流场压力等值线云图Fig. 12 Pressure contours for flow with two rectangles |
脱体激波波后的高温高压低速气体进入两个长 方形之间的槽道流动中。在向右运动过程中压力温 度逐渐减小,速度逐渐恢复。特别是在槽道的核心区位置是典型的连续流区亚声速槽道流动特征。槽道中的气体在长方形后端的扩张作用与外场气体压缩的共同作用下,形成了一片类似于“喷管扩张段”的核心区,该核心区内气体马赫数重新达到并超过1,最高时马赫数恢复到5左右,而压力和速度持续降低,并且形成了上下两道不太对称的压缩波。
从图 12中两个长方形上下物面附近的压力等值线分布能够明显看到一层薄薄的边界层,边界层厚度很小,这正是连续流动的典型特征。
此外,本文还数值计算了稀薄流区(Kn∞=1.0)上下对称尖劈外形(如图 13所示)的复杂流动。来流马赫数Ma∞=3,流动气体为氮气N2。图 14给出了该对称尖劈流场的无量纲密度等值线云图。不仅实现了分区之间流场参数的光滑过渡,高稀薄流动特征也非常明显。壁面干扰在流场中影响范围很广,整个流场没有激波的形成,流场参数缓慢过渡。
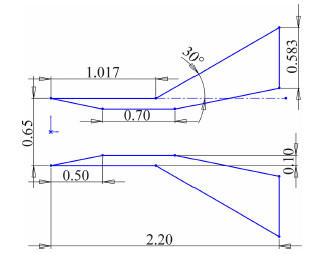 |
| 图 13 上下对称尖劈示意图Fig. 13 Sketch map for symmetrical ramps |
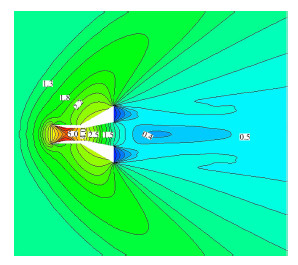 |
| 图 14 对称尖劈流场密度等值线云图Fig. 14 Density contours for symmetrical ramps flow |
在基于Boltzmann模型方程的气体运动论统一算法中应用分区对接网格技术,实现了复杂流场中网格分区之间流场信息的正确传递,以及分区对接面上流场参数的光滑过渡,能够实现对复杂外形的跨流域气体流动问题数值模拟。研究表明,分区对接网格能够实现对包括多体流场在内的复杂流动的正确描述,而且能够更加准确地捕捉流场阶跃、突变、过渡等特征。
| [1] | Wang Baoguo, Liu Shuyan. Calculation study of rarefied aerodynamics[M]. Beijing: Beihang University Press, 2013. (in Chinese) 王保国, 刘淑艳. 稀薄气体动力学计算[M]. 北京: 北京航空航天大学出版社, 2013. |
| [2] | Boltzmann L. Weitere studien uber das warm egleichgewicht unter gas molekulen[J]. Sitzungs Berichte kaiserl. Akad. Der wissenschaften, 1872, 66(2): 275-370. |
| [3] | Gilberto Medeiros Kremer. An introduction to the Boltzmann equation and transport processes in gases[M]. Brazil: Interaction of Mechanics and Mathematics, 2010. |
| [4] | Chapmann S, Cowling T G. The mathematical theory of non-uniform gases[M]. London: Cambridge university Press, 1990. |
| [5] | Bhatnagar P L, Gross E P, Krook M. A model collision processes in gases[J]. Phys. Rev., 1954, 94: 511-525. |
| [6] | Cheremisin F G. A two-level kinetic model for rotational-translational relaxations in a diatomic gas[J]. AIAA 2008-3932. |
| [7] | James Maxwell Buick. Lattice Boltzmann methods in interfacial wave modelling[M]. Philosophy: The University of Edinburgh, 1997. |
| [8] | Xu Kun, Mao Meiliang, Tang Lei. A multidimensional gas-kinetic BGK scheme for hypersonic viscous flow[J]. Journal of Computational Physics, 2005, 203: 405-421. |
| [9] | Li Zhihui, Zhang Hanxin. Study on gas kinetic numerical algorithm using Boltzmann model equation[J]. Advances in Mechanics, 2005, 35(4): 559-576.(in Chinese) 李志辉, 张涵信. 基于Boltzmann模型方程的气体运动论统一算法研究[J]. 力学进展, 2005, 35(4): 559-576. |
| [10] | Li Zhihui, Zeng Shi. Simulation of planar couette flows using the gas-kinetic Boltzmann model[J]. J. of Tsinghua Univ.(Sci. & Tech.), 2005, 45(8): 1103-1106.(in Chinese) 李志辉, 曾实. 基于Boltzmann模型方程的平板Couette流计算[J]. 清华大学学报(自然科学版), 2005, 45(8): 1103-1106. |
| [11] | Li Zhihui, Zhang Hanxin. HPF parallel computation based on Boltzmann model equation for flows past complex body from various flow regimes[J]. Acta Aeronautica et Astronautica Sinica, 2006, 27(2):175-181.(in Chinese) 李志辉, 张涵信. 基于Boltzmann模型方程不同流区复杂三维绕流HPF并行计算[J]. 航空学报, 2006, 27(2): 175-181. |
| [12] | Li Zhihui, Zhang Hanxin. Massive parallelization of gas-kinetic algorithm for Boltzmann model equation[J]. Chinase Journal of Computational Physics, 2008, 25(1): 65-74.(in Chinese) 李志辉, 张涵信. 求解Boltzmann模型方程的气体运动论大规模并行算法[J]. 计算物理, 2008, 25(1): 65-74. |
| [13] | Mao Meiliang, Deng Xiaogang, Xiang Daping. Applied study of method for multi-block patched mesh[J]. Acta Aerodynamica Sinica, 2002, 20(2): 179-183.(in Chinese) 毛枚良, 邓小刚, 向大平. 分区对接网格算法的应用研究[J]. 空气动力学学报, 2002, 20(2): 179-183. |
| [14] | Zhang Zhengke, Zhu Ziqiang, Zhuang Fenggan. Multiblock grid generation technique for multicomponent combination and its application[J]. Acta Aerodynamica Sinica, 1998, 16(3):311-317.(in Chinese) 张正科, 朱自强, 庄逢甘. 多部件组合体分块网格生成技术及应用[J]. 空气动力学学报, 1998, 16(3): 311-317. |
| [15] | Rykov V A. Model kinetic equation of a gas with rotational degrees of freedom [J]. Fluid Dynamics, 1975, 10: 959-966. |
| [16] | Rykov V A, Titarev V A, Shakhov E M. Numerical study of the transverse supersonic flow of a diatomic rarefied gas past a plate [J]. Computational Mathematics and Mathematical Physics, 2007, 47(1): 136-150. |
| [17] | Wu Junlin, Li Zhihui, Jiang Xinyu. Study of one-dimensional shock-tube and two-dimension plate flows by solving Boltzmann-Rykov model equation involving rotational energy[J]. Chinese Journal of Computational Physics, 2013, 30(3): 326-336.(in Chinese) 吴俊林, 李志辉, 蒋新宇. 考虑转动能的一维/二维Boltzmann- Rykov模型方程数值算法[J]. 计算物理, 2013, 30(3): 326-336. |
| [18] | Zhang Hanxin, Shen Mengyu. Computational fluid dynamics—fundamentals and applications of finite difference methods[M]. Beijing: National Defence Industry Press, 2003.(in Chinese) 张涵信, 沈孟育. 计算流体力学—差分方法的原理和应用[M]. 北京: 国防工业出版社, 2003. |
| [19] | Wu Junlin, Li Zhihui, Peng Aoping. Numerical simulation of unsteady flows from rarefied transition to continuum using the gas-kinetic unified algorithm[C]. Xi’an, Shaanxi: CSTAM 2013-A31-1100.(in Chinese) 吴俊林, 李志辉, 彭傲平. 气体运动论统一算法对连续流到稀薄流非定常流场计算研究[C]. 陕西西安: 中国力学大会-2013论文集, 2013, CSTAM2013-A31-1100. |
| [20] | Li Z H, Zhang H X. Study on gas kinetic unified algorithm for flows from rarefied transition to continuum[J]. J. of Comput. Phys., 2004, 193: 708-738. |
| [21] | Larina I N, Rykov V A. On boundary conditions for gases on a body surface[J]. Izv. Akad. Nauk SSSR, Mekh. Zhidk. Gaza, 1986, 5: 141-148. |
| [22] | Ketsdever A, Gnimelshein N. Radiometric phenomena: from the 19th to the 21st century[J]. Vacuum, 2012, 86: 1644-1662. |