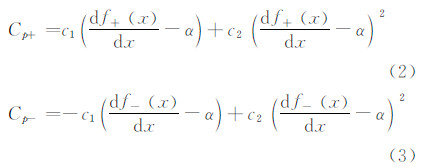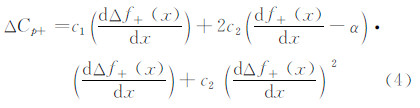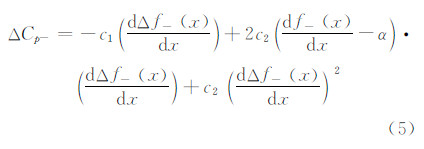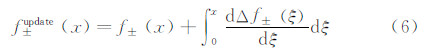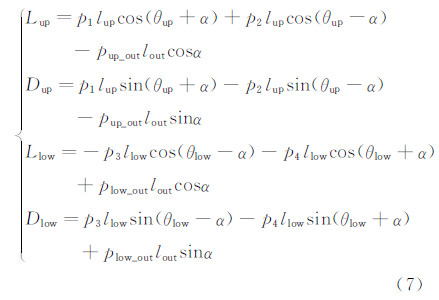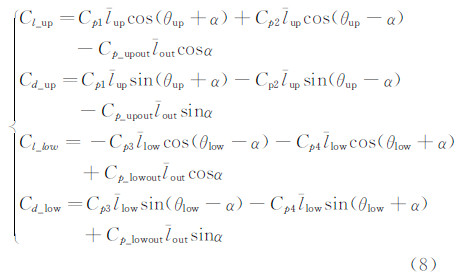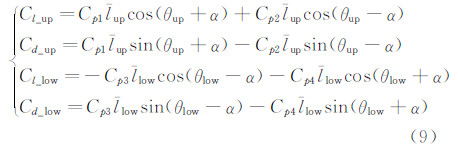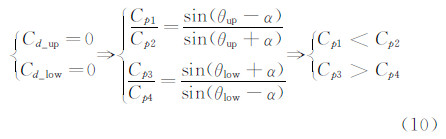0 引 言
升阻比是衡量飞行器气动效率的重要指标之一。超声速飞行器在飞行过程中的强波阻降低了飞行器的升阻比,影响了气动效率,限制了民用和军事领域超声速飞行器的进一步发展。因此,减小激波阻力、提高升阻比对超声速飞行器的发展至关重要。
1935年,第五届Volta空气动力学国际大会上,Busemann首次提出Busemann双翼的概念[1],并于文献[2]中详细描述了消波原理。采用双翼构型,当翼型间距离较近时,双翼间的激波和膨胀波通过相互干涉可以明显降低激波强度,如图1。
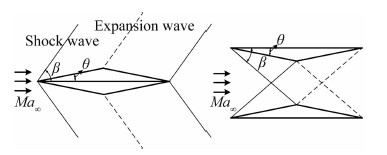 |
| 图 1 Busemann消波原理Fig. 1 Busemann concept |
近几年Busemann消波原理又引起广泛关注,一些学者[3, 4, 5, 6, 7]利用该消波原理提出了一些新概念飞行器的气动布局形式,Jameson等人使用伴随方法优化了该气动构型,解决了流动的壅塞问题[8, 9]。
实际飞行中翼型具有一定迎角,在Busemann建立的理论基础上,Licher提出了非对称Licher双翼[10]。如图2所示,根据叠加原理,将无厚度的平板双翼和上下对称的Busemann双翼相结合,即保证了激波、膨胀波的相对位置,起到消波减阻的效果,又使该翼型具有一定的升力,得到了较大的升阻比。
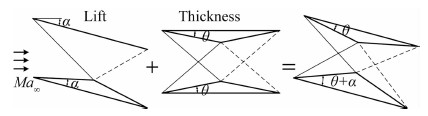 |
| 图 2 Licher双翼设计思路Fig. 2 Licher biplane |
但由于线化理论模型忽略了真实流动中的一些因素,Licher双翼内真实的波系分布不能达到理论预期的效果,因此,有必要对原翼型进行优化。目前梯度法、遗传算法等优化方法在工程上已经大量推广使用[11, 12, 13],但这些方法需要大量的CFD数值模拟结果,因此计算的效率往往不能让人满意。另一种翼型优化方法被称为反设计方法,该方法一般通过给定的目标压力分布求解满足这一压力分布的气动外形,计算效率较高,但也存在难以给定合理的目标压力分布的问题。
超声速Busemann双翼表面的压力分布具有明显的规律,故适合采用反设计方法对其进行优化。日本学者Kusunose教授团队成功的使用了反设计方法优化了Licher翼型,进一步减小了翼型的波阻[4, 14, 15]。
本文完善和发展了Licher双翼的反设计方法,在保留原算法主要框架[4]的基础上,提出翼型修正模块解决优化过程中的边交叉、边界不光滑,算法不收敛等问题;通过非零迎角下的翼型表面的受力分析,提出了一种新的目标压力分布方法,较文献[4]进一步提高了该方法的优化效果;并引入基于NS方程的流场求解器,探究了粘性对该方法的影响。
1 Licher双翼反设计方法原理 1.1 反设计法算法框架图3为反设计方法算法框架,该方法是迭代方法。首先确定初始翼型边界函数f和目标压力系数Cp分布,采用CFD技术求解当前翼型周围流场,确定翼型表面Cp的分布,从而得到压力系数的差值余量ΔCp,构造ΔCp和翼型边界函数变化量Δf之间的关系,确定新的翼型边界函数f。反复重复上述步骤,直到ΔCp < ε(ε为无量纲小量)
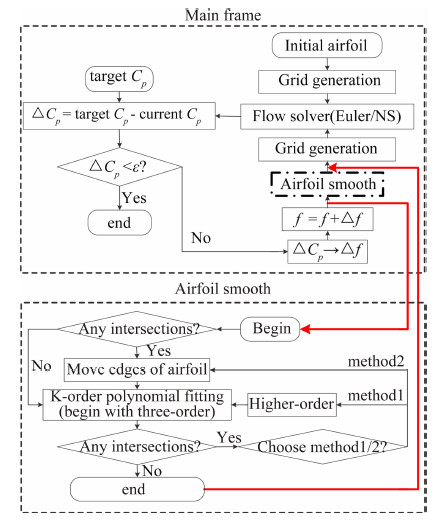 |
| 图 3 反设计优化方法Fig. 3 Inverse design method |
但在实际优化过程中,可能出现ΔCp过大造成的边交叉、边界不光滑或算法不收敛等现象(详见图4),这里提出了一种复合光顺方法对新生成的翼型进行光顺修形(见图3下),通过移动边界解决边交叉问题,采用多项式拟合不光滑边界,具有自适应调整多项式阶数的功能,并可在局部使用直线消除拟合过程中曲线的Runge现象,大量数值实验表明,该光顺方法有效提高了整个优化系统的鲁棒性。
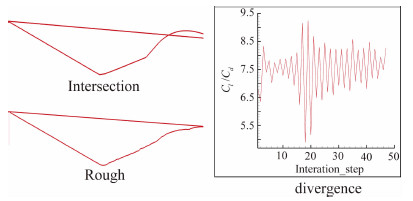 |
| 图 4 无光顺模块的算法缺陷Fig. 4 Setbacks of the method without smoothing airfoils |
基于斜基波关系式[16]可以构造压力系数Cp和翼型表面边界函数f之间的关系[4],θ为壁面楔角(流动转折角):
定义c1、c2为Busemann系数[16],这里Ma∞为来流马赫数,γ为比热比。

可近似认为超声速翼型表面的曲线斜率与自由来流迎角的差等于θ(如图5),故可得翼型上下表面Cp与f之间的关系,这里+代表上表面,-代表下表面,α为来流迎角。
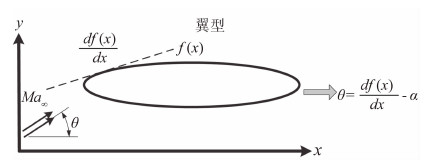 |
| 图 5 翼型与流动方向Fig. 5 Airfoil and flow direction |
进一步得到ΔCp和Δf之间的关系:
求解一元二次方程得 ,对结果进行积分得到优化翼型:
,对结果进行积分得到优化翼型:
翼型的目标压力分布是反设计方法的关键,图6(a)展示了来流马赫数为1.7情况下的Busemann双翼表面的压力系数云图,(b)为压力云图对应的Cp图。分析图6(b)可得,翼型表面Cp分布沿弦向可近似为直线,这是Busemann双翼减小压差阻力的原因。当上下表面Cp完全变为直线,即Cp曲线围成矩形时,翼型的压差阻力为零。文献[4]使用该原理,将优化框架中的目标压力分布定义为矩形(后文简称矩形分布),反复迭代优化,达到减小波阻的效果。
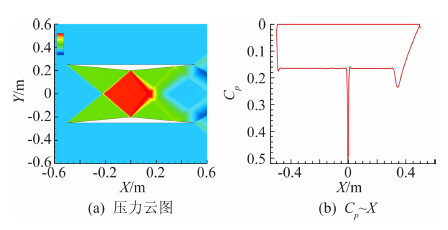 |
| 图 6 Busemann双翼压力分布Fig. 6 Pressure distribution of the Busemann airfoils |
但是,当翼型具有迎角时,矩形目标压力分布具有一定局限性。图7为来流迎角为α的Licher双翼受力分析图,忽略粘性等复杂因素的影响,可分别列出上下翼的升力L和阻力D关系式(7),这里p为翼型表面压力,l为各边长度,d为双翼间距,下标表示变量在翼型上的位置:
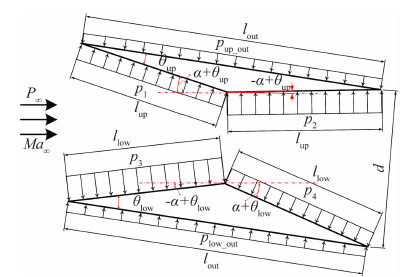 |
| 图 7 Licher双翼受力分析图Fig. 7 Force analyses of Licher airfoils |
根据压力系数Cp=(p-p∞)/q∞,对式(7)进行无量纲化得式(8),其中无量纲长度l=l/lout,Cl、Cd分别表示升力系数和阻力系数。
由于α较小,故Cp_upout<<Cp1(或Cp2),Cp_lowout<<Cp3(或Cp4),式(8)可简化为:
假设上下翼型表面压差阻力均为0,可得:
采用文献[4]做法时,目标Cp分布定义为矩形,对应的Cp1=Cp2;Cp3=Cp4,这显然与式(10)结论相悖。故提出一种新的目标压力分布形式,使Cp1、Cp2、Cp3、Cp4之间的关系满足式(10),如图8所示,Cp分布形似台阶,故简称该种目标压力分布为“阶梯形分布”。
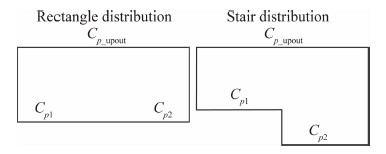 |
| 图 8 上翼目标Cp分布Fig. 8 TargetCp distribution of up airfoil |
由于Cl_up>0;Cl_low < 0,而该目标压力分布会使Cp2相对增大,Cp4相对减小,从而导致Cl_up和Cl_low同时增大。因此,阶梯形分布不仅可让Cd_up→0;Cd_low→0,还可以使双翼升力增大,进一步提高翼型升阻比。
2 计算结果与分析 2.1 基于Euler方程的Licher翼型优化算例初始翼型选取Licher双翼,相关参数见表1(参数具体含义参考图7),翼型表面控制点400个,各点流场状态变量均满足1.2节中的关系式。
| Ma∞ | α/(°) | lout/m | d/m | θup/(°) | θlow/(°) |
| 1.70 | 1.00 | 1.00 | 0.50 | 4.71 | 5.71 |
图9表明,优化后升阻比显著提高,且迭代15步算法基本收敛,说明该反设计方法具有极高的计算效率。表2统计了Licher双翼优化前后的气动力参数,可以看出,采用矩形目标压力分布进行优化未能达到文献的优化效果,对比发现本文优化结果的波阻偏大。而阶梯形分布的优化结果具有高升力特性,显著提高了翼型的升阻比,但阻力相对于矩形分布优化结果有明显增加。
 |
| 图 9 基于Euler方程的优化方法收敛性Fig. 9 Convergence of the optimization method based on Euler equations |
为进一步探究两种目标压力分布下不同优化效果的产生机理,分析优化前后翼型周围流场。图10为优化前流场,该图表明:线化理论设计的Licher双翼间的波系与理论估计有所差异,翼型前缘形成的激波打在了转折点前方,形成了Cp图上的第一个压力峰值;第一个激波的前移造成了反射激波与膨胀波的错位,反射的激波打在翼型后缘,形成了Cp图的第二个压力峰值;翼型后缘产生的膨胀波使得Cp值急剧减小。因此Licher双翼未能达到预期的减阻效果。
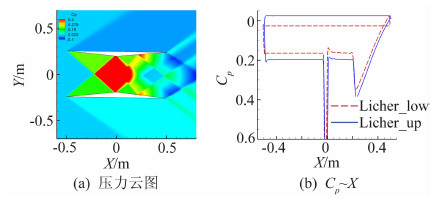 |
| 图 10 Licher双翼压力分布Fig. 10 Pressure distribution of the Licher airfoils |
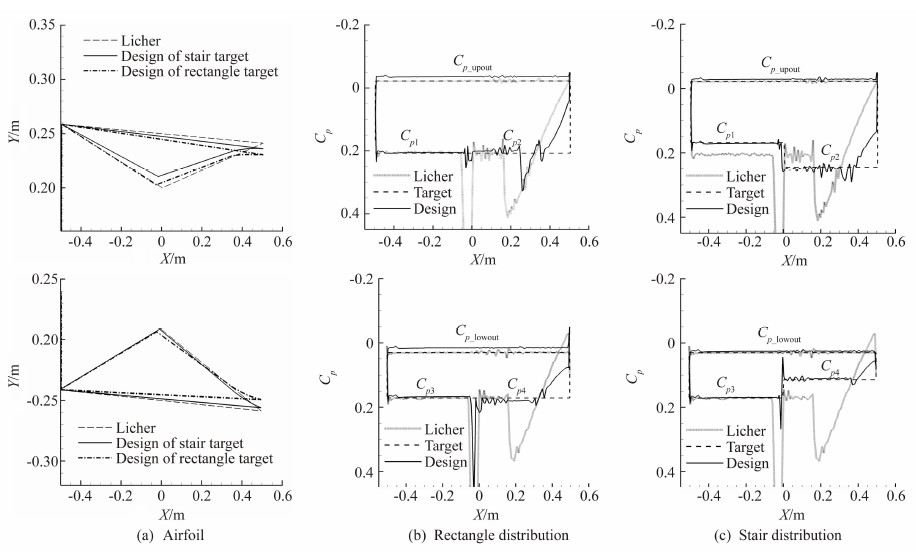
图11表明以矩形Cp分布为目标优化后,上下翼型被削薄,翼型内侧流动转折点前移,前缘形成的激波打在转折点处,消去了第一个Cp峰值;通过控制后 缘翼型内侧形状,使反射激波与膨胀波重合,消去第二个Cp峰值;同时改变翼型后缘曲率,降低了Cp曲线的衰减程度,从而达到减小阻力的作用。与矩形目标压力分布类似,阶梯形目标压力分布也削平了Licher双翼内侧的Cp峰值,减小了阻力,但翼型弯度较矩形优化结果有所增加。
 |
| 图 11 基于Euler方程的翼型优化结果Fig. 11 Optimization results based on Euler Equations |
对比图12(a)与图12(b),图(a)Cp1、Cp3和Cp2、Cp4区域颜色基本相同,图12(b)相对于图12(a),Cp2区云图颜色变深,上翼内侧压力系数增大,Cp4区云图颜色变浅,下翼内侧压力系数减小,该分布有效增加了双翼升力,使升阻比进一步提高,这与1.3节的理论分析的结果一致。
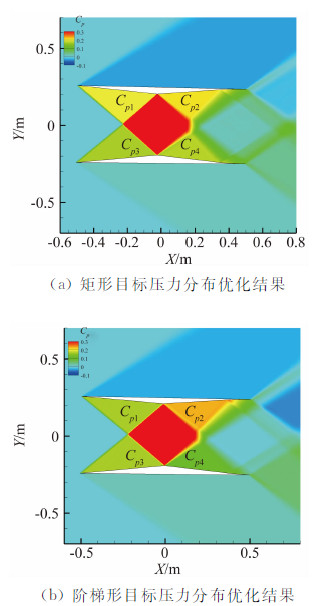 |
| 图 12 基于Euler方程优化结果的压力云图Fig. 12 Pressure contours of optimization airfoils based one Euler equations |
为探究阶梯形目标优化结果阻力偏大的原因,分别将上下翼阻力系数列于表3中,可得,在矩形目标分布下,下方翼型水平方向气动力呈推力状态,有效地减少了阻力。因此,矩形分布的优化结果侧重于低波阻,而阶梯分布的优化结果侧重于高升力。
| Cd | rectangle design | stair design |
| Up airfoil(×10-3) | 5.39 | 2.43 |
| Low airfoil(×10-3) | -1.45 | 1.92 |
| Sum(×10-3) | 3.94 | 4.35 |
优化结果仅给出设计迎角α=1°下的翼型升阻特性,保持来流马赫数不变,分别计算三种翼型在0°~4°迎角下的升阻特性。由图13可得:优化设计的双翼具有较好的稳健性,在迎角0°~4°的变化范围内没有出现流动壅塞现象[5, 8, 9];同时,设计状态下具有较高升阻比的翼型,在其它迎角下升阻比仍占据优势。
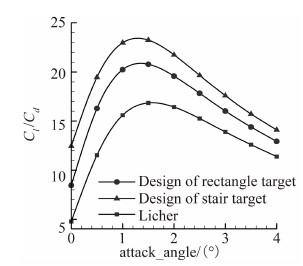 |
| 图 13 不同迎角下的升阻比Fig. 13 Lift-drag ratio of different angles |
为了探究粘性对双翼性能的影响,使用基于NS 方程的CFD求解器代替优化框架中的Euler方程求 解器,雷诺数Re=3.8×107,选择SST湍流模型,翼型数据,来流马赫数,来流迎角等初始条件均保持不变。
对比表2和表4的升阻比变化率可得,考虑粘性后,阶梯分布优化结果的优势更加明显,相对矩形分布优化的结果,其升阻比提高率达到了32.2%,远高于无粘情况下19.3%。为分析原因,将阻力分解成摩擦阻力和激波阻力(如图14)。图14表明:与菱形翼对比,双翼构型使激波阻力减小了约一个量级,但摩擦阻力却增加了两倍,阶梯分布优化结果的特点是高升力,而矩形分布优化结果的特点是低波阻,考虑粘性后,摩擦阻力在阻力中占据主导的地位,减小波阻提高升阻比的效果受到抑制,因此矩形分布的优化效果变差。但阶梯形分布具有高升力特性,仍可保持良好的优化效果,故以阶梯形分布为目标的反设计方法更具实用价值。
| Licher | Rectangle design | Stair design | |
| Cl(×10-2) | 8.48 | 8.52 | 11.10 |
| Cd(×10-2) | 1.34 | 1.15 | 1.18 |
| Cl/Cd | 6.30 | 7.38 | 9.41 |
| Increment | - | 17.0% | 49.2% |
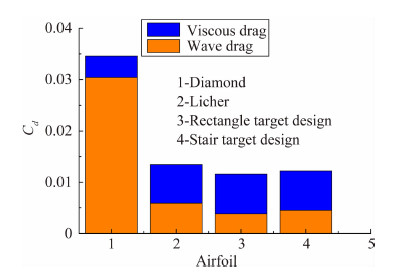 |
| 图 14 阻力分解Fig. 14 Drag analyses |
图15为基于NS方程的翼型优化结果,对比图11中的无粘优化结果可以看出,Cp分布规律基本保持不变,且阶梯形目标压力分布优化的翼型弯度仍大于矩形分布的优化结果。但由于边界层效应,Licher双翼内侧的两个压力峰明显前移,导致优化翼型的转折点前移,此外,激波(膨胀波)边界层干扰,边界层流动转捩等复杂流动现象使得计算出的翼型表面Cp值出现波动,影响了优化稳定性,削弱了减阻效果。
 |
| 图 15 基于NS方程的翼型优化结果Fig. 15 Optimization results based on NS Equations |
采用反设计方法,结合CFD技术,对Licher双翼进行了优化设计,得到以下结论:
1) 反设计方法有效修正了线化理论和实际流动之间的差异,提高了Licher双翼的升阻比;且该方法的计算效率极高,一般迭代不超过20步,即可得到收敛的结果。
2) 目标压力分布是反设计方法中的关键因素,矩形目标压力分布可以有效减小激波阻力,来流马赫数1.7、无粘情况下使升阻比提高30.5%。但该分布在翼型有迎角的情况下存在不足,本文提出阶梯形目标压力分布,在保留消波减阻特性的基础上,增加了双翼升力,无粘假设下升阻比可提高49.8%。
3) 当上述优化方法推广到粘性情况下进行设计时,由于摩擦阻力在阻力中占主导地位,矩形目标压力分布优化效果受到抑制,来流马赫数1.7时升阻比仅能提高17%,而阶梯形分布的优化效果受到影响较小,升阻比仍可提高49.2%,因此阶梯形目标压力分布更具实用价值。
| [1] | Busemann A. Aerodynamic lift at supersonic speeds[C]. The 5th Volta Aerodynamic Conference, Volta, Italy, October 3, 1935. |
| [2] | Busemann A. The relation between minimized drag and noise at supersonic speed[C]. The High-speed Aeronautics Conference. Brooklyn, USA, January 20-22, 1955. |
| [3] | Xu Y Z, Xu Z Q, Li S G, et al. A hypersonic lift mechanism with decoupled lift and drag surfaces[J]. Science China:Physics, Mechanics & Astronomy, 2013, 56(5):981-988. |
| [4] | Kusunose K. A fundamental study for the development of boomless supersonic transport aircraft[C]. The 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, USA, January 9-12, 2006. |
| [5] | Maruyama D, Matsuzawa T. Consideration at off-design conditions of supersonic flows around biplane airfoils[C]. The 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, USA, January 8-11, 2007. |
| [6] | Yonezawa M, Yamashita H, Obayashi S. Investigation of supersonic wing shape using Busemann biplane airfoil[C]. The 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, USA, January 8-11, 2007. |
| [7] | Hua Ruhao, Ye Zhengyin. Drag reduction method for supersonic missile based on Busemann biplane concept[J]. Chinese Journal of Applied Mechanics, 2012, 29(5):536-540. (in Chinese)华如豪, 叶正寅. 基于Busemann双翼构型的超音速导弹减阻技术研究[J]. 应用力学学报, 2012, 29(5):536-540. |
| [8] | Hu R, Jameson A. Wang Q Q. Adjoint-based aerodynamic optimization of supersonic biplane airfoils[J]. Journal of Aircraft, 2012, 49(3):802-814. |
| [9] | Hu R. Supersonic biplane design via adjoint method[D]. Stanford:Institution of aeronautics and astronautics, 2009. |
| [10] | Licher R M. Optimum two-dimensional multiplanes in supersonic flow[C]. Douglass Aircraft Conference, USA, 1955. |
| [11] | Ye Youda, Luo Tianning, Lu Shen, et al. Application of optimization method based on dynamic boundary control in configuration optimization of high lift-to-drag vehicle[J]. Acta Aerodynamica Sinica, 2009, 27:29-33. (in Chinese)叶友达, 罗天宁, 卢笙, 等. 基于动态边界控制的优化方法在高升阻比气动外形优化中的初步应用[J]. 空气动力学学报, 2009, 27:29-33. |
| [12] | Chang Yanxing, Gao Zhenghong. Applicability analysis of genetic algorithms using in aerodynamic optimization[J]. Acta Aerodynamica Sinica, 2009, 27(2):167-172. (in Chinese)常彦鑫, 高正红. 遗传算法在气动优化问题中的适应性分析[J]. 空气动力学学报, 2009, 27(2):167-172. |
| [13] | Li Jing, Gao Zhenghong, Huang Jiangtao, et al. Airfoil optimization based on distributed panicle swarm algorithm[J]. Acta Aerodynamica Sinica, 2011, 29(4):464-469. (in Chinese)李静, 高正红, 黄江涛, 等. 基于分布式粒子群算法的翼型优化设计[J]. 空气动力学学报, 2011, 29(4):464-469. |
| [14] | Matsushima K, Takanashi S. An inverse design method for wings using integral equations and its recent progress[C]. Proceedings of Lectures and Workshop International Recent Advances in Multidisciplinary Technology and Modeling, Japan, 2008. |
| [15] | Kusunose K, Matsushima K, Maruyama D. Supersonic biplane-a review[J]. Progress in Aerospace Sciences, 2011, 47:53-87. |
| [16] | Liepmann H W, Roshko A. Elements of gas dynamics[M]. New York:John Wiley & Sons, Inc, 1957. |
| [17] | Yamashita H, Yonezawa M, Obayashi S, et al. A study of Busemann-type biplane for avoiding choked flow[C]. The 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, USA, 2007. |