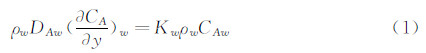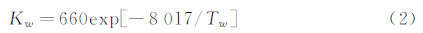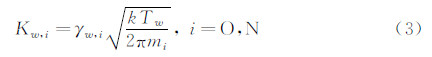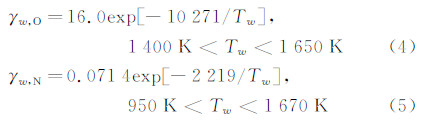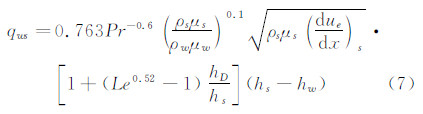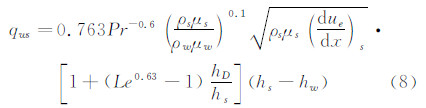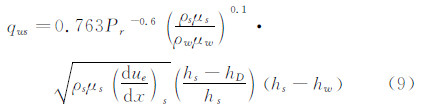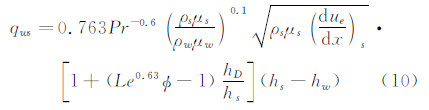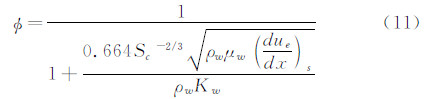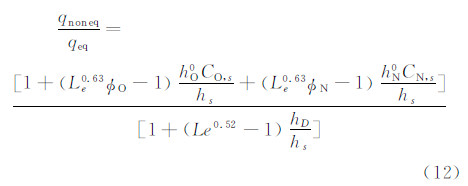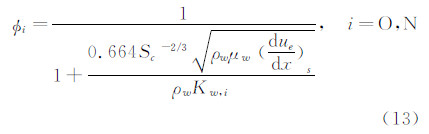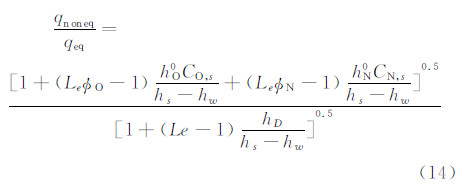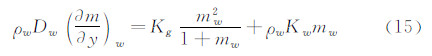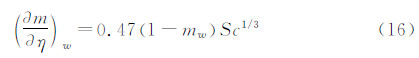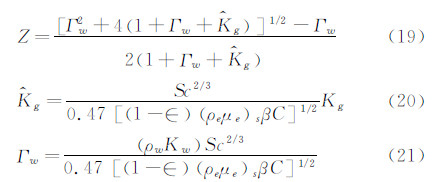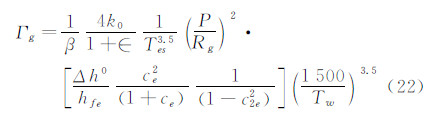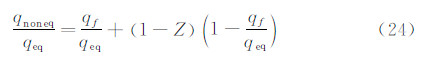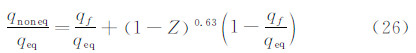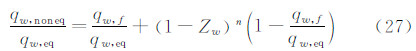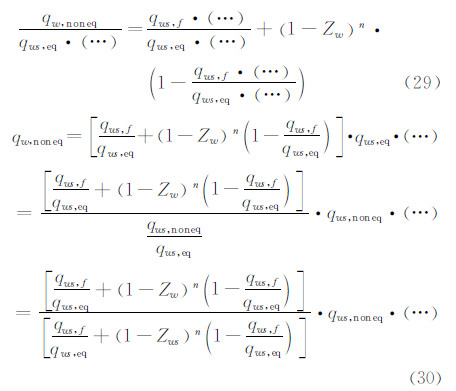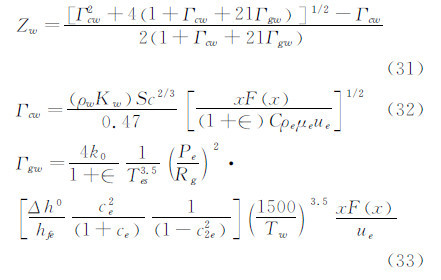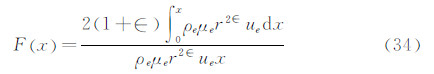0 引 言
高超声速或高温流动依据流动特征时间与振动松弛和化学反应特征时间的相对大小可区分为冻结、平衡和非平衡流动，平衡流和冻结流是非平衡流动的两种极限状态。对航天飞机或宇宙飞船等高超声速再入飞行器而言，最大加热率发生在60～70 km附近[1, 2]，而此时飞行马赫数往往很高，由于强激波的作用，会导致激波后空气分子被剧烈加热而产生离解和电离，由于这一高度范围的大气比较稀薄，原子或离子穿过边界层时碰撞不充分，往往来不及完全复合就到达飞行器表面，边界层内的流动处于热化学非平衡状态，此时在边界层内和表面上的化学复合能将对飞行器热环境产生很大影响。有关试验表明[3]，在某种情况下，非平衡和表面催化效应可使当地热流降低35％以上。因此，建立非平衡热环境快速估算方法，对于飞行器热环境准确预测和防热设计具有重要意义。
如何准确给出非平衡热环境是气动热研究中的一大技术难点。由于非平衡热环境试验研究难度较大，可用的设备不多，因此长期以来，有关非平衡热环境试验，特别是关于表面材料催化特性对热环境影响的试验研究开展的较少，数据积累不多。目前，人们主要通过计算手段研究非平衡效应，而计算分为工程方法[3, 4, 5]和数值方法[6, 7, 8]两种。工程计算具有快速可靠等优点，是型号研制中获取气动热数据的主要手段。目前，国内有关热化学非平衡的气动热环境工程计算主要借鉴于国外文献给出的相关性公式[3, 9]，但研究表明，现有的众多非平衡热流工程计算方法，都或多或少存在一些问题，采用不同方法给出的计算结果相互之间差别较大，有的低估了非平衡效应，而大部分方法都高估了非平衡效应。
早期工程方法[3]在估算非平衡热环境时，通常认为边界层内流动的化学状态是完全冻结的，边界层外缘的氧原子和氮原子全部扩散到壁面，并在壁面上发生原子复合反应，反应过程取决于壁面催化特性。如果壁面对原子复合是非催化的，则化学反应对壁面热流没有贡献，热流值最低；如果壁面是完全催化的，壁面原子浓度将降低到壁面条件下的平衡值。大量研究表明，冻结边界层完全催化壁条件下的热流与平衡边界层的壁面热流非常接近，热流达到最大值。但大多数壁面是属于任意催化的，此时壁面热流中的化学贡献部分完全取决于壁面上的原子复合速率。因此，对于冻结边界层，壁面催化特性对于壁面热流的影响是很重要的，选择低催化效率的壁面材料可以使壁面热流大大降低，在某种情况下，非催化壁热流仅为完全催化壁热流的30％～65％。因此，早期热流工程计算中所讨论的热化学非平衡效应，主要指的是冻结边界层的催化效应，而非边界层内的非平衡效应。
但实际上，边界层内化学反应不可能是完全冻结的，建立能同时考虑边界层内化学反应和表面催化特性的非平衡热环境快速估算方法更符合实际要求。研究表明[10, 11, 12]，边界层中的原子复合反应主要发生在靠近壁面的薄层内，根据这一特点，可以将边界层中的气相反应等价到表面上，由此可以建立同时考虑边界层非平衡反应和表面催化特性的非平衡边界层气动加热快速计算方法。在此基础上，本文借鉴国外材料催化特性数据，采用完全催化壁、完全非催化壁及有限催化壁模型，针对美国航天飞机[2]和欧洲钝锥标模[13]进行了计算分析，给出了非平衡流及催化特性对气动热环境影响的计算结果。
1 非平衡边界层气动加热计算方法 1.1 非平衡边界层气动加热计算方法对非平衡加热，材料的催化特性影响十分显著，在某种情况下，非催化壁热流仅为完全催化壁热流的30％。大多数壁面都属于任意催化壁，热流中的化学贡献部分取决于壁面上的原子复合率。在定常情况下，扩散到壁面的原子净质量流等于单位时间单位表面上的原子质量复合率，即:
其中，Kw为壁面催化速率常数，m/s；CAw为A原子在壁面上的质量浓度。上式即为扩散方程在双原子气体情况下的壁面边界条件。对于完全催化壁，Kw→∞，CAw→0；对于非催化壁，Kw→0，∂CA/∂y→0；对于有限催化壁，Kw的值与壁温和材料性能有关。对于美国航天飞机上所用的RCG涂料，文献[3]给出了Kw与壁温的关系:
在一些文献中，度量壁面的催化程度，不采用上式表示的催化反应速率常数Kw，而是采用所谓复合催化效率γ，它定义为单位时间单位面积上复合的原子数与单位时间撞击单位面积的总原子数之比，它与Kw之间有如下关系:
这里k为Boltzmann常数，mO和mN分别为氧原子和氮原子的质量。文献[3]根据RCG涂层的有关试验数据给出的氧原子和氮原子复合催化效率γw,O和γw,N同壁温的关系为: 1.2 冻结边界层的驻点气动加热计算方法
早期人们主要采用冻结边界层加表面催化的方法估算非平衡热环境。有关文献提供了多种化学非平衡气动加热计算方法，这里列出了其中四种方法：
(1) 方法1
文献[3]给出了一个较为简便且具有较好精度的化学非平衡驻点热流计算公式，为:
其中,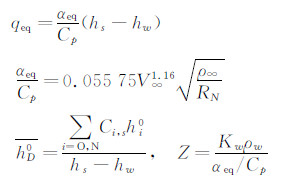
(2) 方法2
对平衡边界层，著名的Fay-Riddell驻点热流公式为:
对冻结边界层，在完全催化壁和非催化壁条件下，有在形式上与平衡边界层驻点热流公式相类似的驻点热流计算公式。
完全催化壁：
非催化壁:
比较公式(7)和(8)可以看出，两个公式的唯一差别在Le数的方次略有不同，因为Le数本身接近于1，从而可以得出这个结论:平衡边界层驻点热流与冻结边界层完全催化壁驻点热流是很接近的，这个结论为后来的大量计算所证实。
对于冻结边界层任意催化壁，文献[12]在高冷壁和各组元定压比热Cpi都相等的合理近似下，求得了冻结边界层的分析解，然后用完全催化壁的精确解来修正其结果，得到了冻结边界层有限催化壁的驻点热流公式:
其中,φ为驻点处壁面催化因子，由下式给出:
式中，Kw为壁面催化速率常数，Sc为斯密特数(=Pr/Le)。当Kw→∞时，φ→1，相当于完全催化壁；当Kw→0时，φ→0，相当于非催化壁。Kw的值与表面防热材料性能有关，由实验确定。
(3) 方法3
对于冻结边界层完全催化壁、非催化壁和有限催化壁，Fay和Riddell[14]给出了已被广泛应用的驻点热流公式(8)、(9)和(10)。但是，应当指出，那些结果是在二组元假定下(即气体原子和分子)得到的，即在处理边界层方程时，不去具体区分氧的原子和氮的原子，或氧的分子和氮的分子，而有些文献则分别考虑了氧原子和氮原子的壁面催化速率常数和，他们给出了对应的冻结边界层有限催化壁与平衡条件下的驻点热流比:
其中, 这里Kw,O和Kw,N分别为壁面对氧原子和氮原子的催化速率常数，它们同复合催化效率有关。
(4) 方法4
潘梅林[3]也给出了一个冻结边界层有限催化壁与平衡条件下的驻点热流之比的公式，取得了与飞行试验更为接近的计算结果：
1.3 非平衡边界层的驻点气动加热
对于发生在边界层内的化学反应，研究表明，对于高冷壁情况，边界层中的原子复合反应主要发生在靠近壁面的薄层内，因此可以将边界层中的气相反应等价到表面上。
对于任意催化壁，同时考虑原子气相复合反应和壁面催化复合反应的边界层内原子扩散方程为：
其中Kg为气相反应的等价表面反应常数，m=c/ce，c为原子的质量分数。由于我们将边界层内的非平衡气相反应等价到表面上，因此可以认为边界层内化学冻结，对于冻结边界层，扩散方程的精确解为： 这里：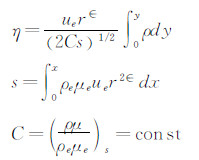
对于Lewis数偏离1不大的情况，以下关系式成立：
其中，q、qf、qeq分别为非平衡边界层、冻结边界层和平衡边界层表面热流。
联合求解式(15)、(16)和(17)得：
其中， 对于轴对称驻点，Goodwin[9]给出了(q-qf)/(qeq-qf)的另一个关联参数Γg取代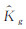
(见图1):
 |
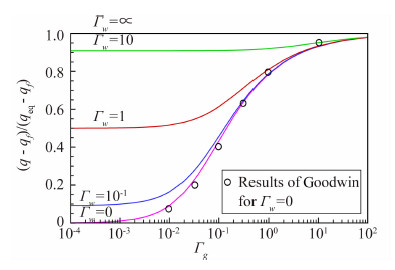| 图 1 (q-qf)/(qeq-qf)随变量Γg和Γw 的变化情况Fig. 1 Varation of heatflux with respect to Γg and Γw |
计算表明，如果取:
得到的热流关联与图1一致。这样就可以采用(18)式计算非平衡边界层传热了，可以同时考虑边界层内的气相反应和表面催化效应。其中Γg和Γw是非平衡边界层的Damkholer数，分别代表气相和表面反应的扩散特征时间与化学反应特征时间之比。
根据式(18)，非平衡热流与平衡热流的比值，即非平衡热流放大系数为:
其中qf和qeq分别采用Fay-Riddell冻结边界层完全非催化壁和平衡边界层热流公式(12)计算。这里将式(24)称为方法5。
借鉴方法4的处理方式，将式(24)右边项用n次方形式替换，用飞行数据去拟合，则:
根据STS-2飞行测量结果拟合的结果，n＝0.5～1，我们建议取n＝0.63，则有: 该式为方法6。 1.4 驻点下游的非平衡边界层气动加热
对于驻点下游的边界层加热，可以借鉴驻点的非平衡热流计算方法，即:
考虑到: 则 这里取[15]: 其中： 这样就可以采用式(30)计算驻点下游非平衡边界层传热了，可以同时考虑边界层内的气相反应和表面催化效应。其中Γgw和Γcw是非平衡边界层的Damkholer数，分别代表气相和表面反应的扩散特征时间与化学反应特征时间之比。 2 方法验证和计算结果分析 2.1 美国航天飞机计算结果
图2给出了针对美国航天飞机STS-2[2]采用不同计算方法得到的迎风中心线不同位置处非平衡热流与飞行测量结果的比较，可以看出，方法1、2、3结果基本一致，方法5结果略好于他们。对于X/L=0.025处，这4种方法在高空段都高估了非平衡效应。方法4和方法6对高空段进行了修正，但中间段比实测结果高。通过不同位置的综合比较，可以看出，本文给出的方法6结果与飞行测量结果符合的最好，虽然个别地方计算的热流略高于实测热流，但从飞行安全角度考虑，方法6结果是合适的，因此建议采用方法6。从图中可以看出，化学非平衡效应的影响主要发生在55 km高空飞行阶段，此时壁面处于有限催化到完全非催化之间的状态，更接近于完全非催化。随着飞行高度的降低，化学非平衡效应也在下降，50km以下，基本上处于化学平衡状态。
 |
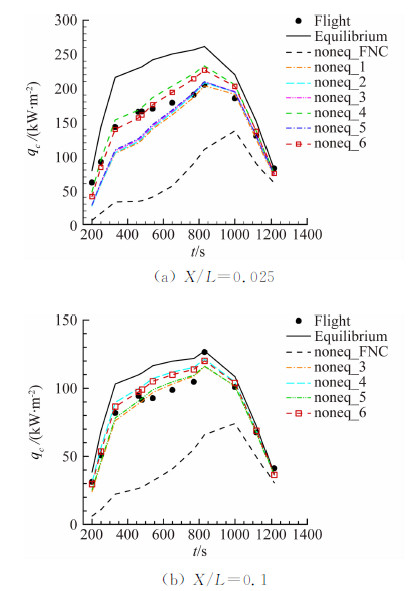| 图 2 不同方法计算的化学非平衡热流(STS-2)Fig. 2 Comparison of non-equilibrium heatflux for STS-2 using different methods |
图3给出了头部半径为1 ft、H=60 km、马赫数M∞=24.4时情况下，采用不同的计算模型计算的球双锥轴向热流分布情况。其中qeq、qf、qnoneq=Knoneq,s·qeq、qnoneq=Knoneq·qeq分别为按平衡边界层、冻结边界层完全非催化、任意催化条件下利用驻点的非平衡效应进行修正、沿物面根据当地非平衡效应进行适时修正得到的表面热流分布情况的比较。可以看出，平衡边界层结果显著高于冻结边界层完全非催化壁结果，它们给出了上下边界，任意催化壁结果介入平衡和冻结非催化壁之间。如果弹体表面都按照驻点的非平衡效应进行修正，那么在远离驻点的地方会高估了非平衡效应，这是因为驻点下游球面上，由于表面压力迅速下降，气流急剧膨胀加速，因此球面边界层基本处于冻结状态，但在球头下游，特别是锥面上，由于压力不再急剧变化，边界层逐渐趋于平衡状态，热流也趋于平衡值，这一点已经被试验和数值计算结果所证实。从图4的局部放大图可以看出，本文方法能够正确地反映这一过程。
 |
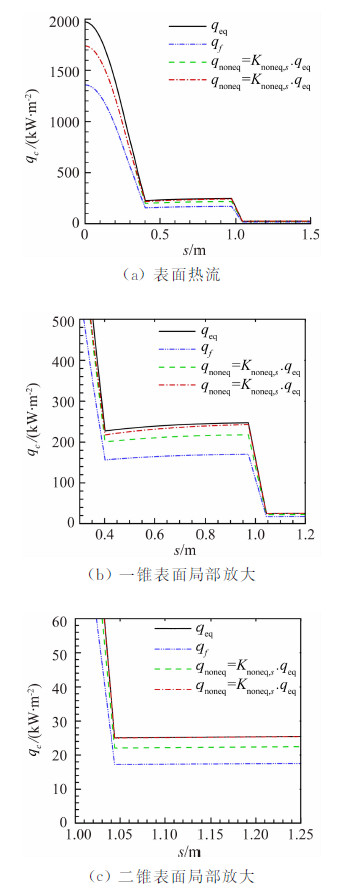| 图 3 非平衡效应对飞行器迎风母线热流的影响Fig. 3 Comparison of non-equilibrium windward heatflux using different methods |
 |
| 图 4 本文计算的热流与飞行数据和数值模拟结果的比较Fig. 4 Comparison of calculated results with flight and numerical data |
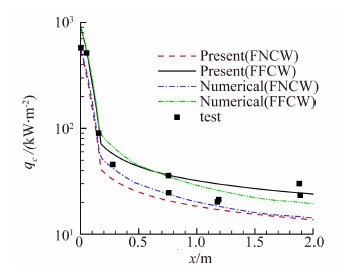
国外常用钝锥标模ELECTRE的飞行试验测量结果[13]来考核热环境地面试验和计算结果，飞行试验模型是总长度为2m，头部半径为0.175m，半锥角为4.6°，模型上布置了10个测热点T1至T10。图4给出了本文提出的新方法(方法6)计算的热流与飞行数据和数值模拟结果[8]的比较，这里同时给出了完全非催化壁面条件(FNCW)和完全催化壁面条件(FFCW)的计算结果，可以看出，工程计算与数值模拟结果基本一致，飞行试验数据除尾部一个点外大都在两者之间，这说明了计算的准确性是非常好的。
3 结 论本文通过对飞行器表面热环境计算分析，得出如下几点结论：
(1) 在50 km以上高空飞行阶段，非平衡效应与稀薄气体效应同时发生。在50～80 km范围内，边界层内的化学反应主要发生在靠近壁面的薄层内，可以将边界层中的气相反应等价到表面上，从而进一步将热化学非平衡边界层简化为具有有限催化壁的冻结边界层处理，据此建立了同时考虑边界层非平衡反应和表面催化特性的非平衡边界层气动加热快速计算方法。
(2) 平衡边界层结果显著高于冻结边界层完全非催化壁结果，它们给出了上下边界，任意催化壁结果介于平衡和冻结非催化壁之间。如果机身表面都按照驻点的非平衡效应进行修正，那么在远离驻点的地方会高估了非平衡效应，因为下游边界层逐渐趋于平衡状态。
(3) 文献中给出了许多非平衡热流工程计算方法，但采用不同方法给出的计算结果相互之间差别较大，有的低估了非平衡效应，而大部分方法都高估了非平衡效应。本文建立的新方法给出的热流计算结果与数值模拟和飞行试验测量结果都有很好的一致性。
| [1] | Williams S D. Colunbia:the first five flights entry data series, Volume 3, the lower windward surface centerline[R]. NASA CR-171665, 1983. |
| [2] | Dacid A S. Catalytic surface effects on space shuttle thermal protection system during earth of flights STS-2 through STS-5[R]. NASA CP-2283, Part2, 1983:827-846. |
| [3] | 张志成, 潘梅林, 刘初平. 高超声速气动热和热防护[M]. 北京:国防工业出版社, 2003. |
| [4] | Inger G R. Nonequilibrium viscous shock-layer heat transfer with arbitrary surface catalycit[J]. Journal of Spacecraft and Rockets, 2005, 42(2):193-200. |
| [5] | Hamillton H H, Weilumenster K J, DeJarnette F R, et al. Approximate method for computing the effect of a finite catalytic wall on laminar heating rates in an equilibrium air flowfield[R]. AIAA 2012-0535, 2012. |
| [6] | Park C. Nonequilibrium hypersonic aerothermodynamics[M]. Wiley, N Y, 1990. |
| [7] | Holden M S, Harvey J K, Cander G V. Camparisons between measurements in regions of laminar shock wave boundary layer interaction in hypersonic flows with Navier-Stokes and DSMC solutions[R]. AIAA 2002-0435. |
| [8] | Dong Weizhong, Ding Mingsong, Gao Tiesuo, et al. The influence of thermo-chemical non-equilibrium model and surface temperature on heat transfer rate[J]. Acta Aerodynamica Sinica, 2013, 31(6):692-698. (in Chinese)董维中, 丁明松, 高铁锁, 等. 热化学非平衡模型和表面温度对气动热计算影响分析[J]. 空气动力学学报, 2013, 31(6):692-698. |
| [9] | 卞荫贵, 钟家康. 高温边界层传热[M]. 科学出版社, 1986. |
| [10] | Goodwin G, Chung P M. Effects of nonequilibrium flows on aerodynamic heating during entry into the earth's atmosphere from parabolic orbits[J]. Advances in Aeronautical Sciences(Pergamon Press, New York, 1961, 4:997-1018. |
| [11] | Inger G R. Nonequilibrium-dissociated stagnation boundary-layer flow on a arbitrarily catalytic swept wing[J]. AIAA J., 1995, 33(10):1836-1841. |
| [12] | Wang Z H, Bao L, Tong B G. Theoretical modeling of the chemical non-equilibrium flow behind a normal shock wave[J]. AIAA J., 2012, 50(2):494-499. |
| [13] | Muylaert J, Walpot L, Hauser J. Standard model testing in the european high enthalpy facility F4 and extrapolation to flight[R]. AIAA-92-3905, 1992. |
| [14] | Fay J A, Riddell F R. Theory of stagnation point heat transfer in dissociated air[J]. J. Aeronaut Sci., 1958, 25(2):73-85. |
| [15] | Inger G R. Recombination-dominated nonequilibrium heat transfer to arbitrarily-catalytic hypersonic vehicles[R]. AIAA-89-1859, 1989. |