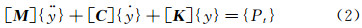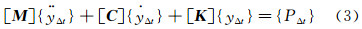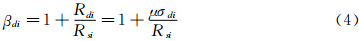2. 中南建筑设计院股份有限公司, 湖北 武汉 430071
2. Zhongnan Construction Design Institute Co., Ltd, Wuhan 430071, China
0 引 言
近年来,大跨屋盖由于具有诸多优点而被广泛应用在体育场、大型展览馆和机场航站楼等建筑结构,而跨度大、自重轻、结构柔以及自振频率低等特点使得其对风荷载的敏感度大大增强。在一般情况下,风荷载往往已成为结构设计的控制荷载。因此,在建筑荷载规范不完善的情况下,采用风洞试验的方法去获取大跨屋盖的风荷载分布特性显得尤为必要。
目前,在大跨屋盖的平均风压分布特性方面,国内外开展了许多风洞试验研究[1, 2, 3, 4],取得了一定成果。但这些建筑物的造型各异,导致其风压分布特性存在一定差异。而在大跨屋盖非高斯风压分布特性方面,国内研究者也进行了一定的研究,如孙瑛等[5]探讨了大跨度平屋盖非高斯特性的原因,并结合第三、四阶统计量,给出了划分高斯与非高斯区域的标准。叶继红等[6]结合五种典型形式大跨屋盖的风洞试验,分别采用了统计方法和基于k-s检验的曲线拟合方法对屋盖进行了高斯与非高斯分区。上述非高斯特性的研究只针对于一些比较理想的屋盖模型,对于实际比较复杂的大跨屋盖非高斯特性还研究的比较少。在大跨屋盖的等效静风荷载方面,目前理论比较合理的计算方法如荷载响应相关方法(Load Response Correlation,简称LRC)[7, 8]与等效目标的选取存在很大的关系,不同的等效目标会导致不同的等效静风荷载,且该方法的计算也比较复杂,进而影响了它的发展。阵风因子法(Gust Load Factor,简称GLF)[9]由于概念明确在高层建筑等效静风荷载分析中得到了非常广泛的应用。而大跨屋盖由于不同响应之间的影响面差异较大,导致该方法的计算精度与其在高层建筑的应用结果相比存在一定差异,但是其误差仍然可被工程所接受。鉴于此,陆锋等[10]采用谱分析方法计算了结构的风振响应和风振系数,得出了大跨平屋面各节点位移风振系数变化不大的结论,并建议在工程实践中使用位移风振系数计算等效静风荷载。李庆祥等[11]则采用时域的直接积分法计算了单层网壳的位移风振系数,并认为风振系数随风向角变化较大。田玉基等[12]采用了振型叠加法计算了上吸风的风振系数,并提出了下压风振系数的概念及计算方法。潘峰等[13]采用多阶模态加速度法计算了结构的荷载风振系数和位移风振系数,并将计算结果与时域积分法计算出的结果进行了对比。由此可见,对于工程实际而言,采用风振系数计算等效静风荷载仍然具有较大的适用性。
本文以某机场航站楼为工程背景,首先通过风洞试验得到其平均风压分布特性,并对航站楼的重要部位如大悬臂挑檐、天井和悬空屋盖的风压分布特征进行了详细的阐述。然后,基于风压的统计特征,对整个航站楼屋盖进行了高斯与非高斯分区。最后,在整体模型位移风振系数计算结果的基础上,着重对风振响应比较大的悬空屋盖区域进行局部风振响应分析,并将局部分析的位移风振系数计算结果与整体模型进行了对比。
1 项目概况与风洞试验某机场新航站楼的平面尺寸约为1 200 m×360 m,航站楼楼盖及下部结构采用钢筋混凝土结构。屋盖为钢网架结构,呈自由曲面,其最高点高度为41 m,向东、西方向逐渐降低,主出入口处屋面檐口悬挑最大长度约40 m。屋盖结构与下部结构通过钢立柱连接,形成协同受力体系,周边围护结构均为玻璃幕墙。
风洞试验是在西南交通大学风工程试验研究中心XNJD-3号风洞进行的,鉴于试验需要模拟周围特征建筑物,考虑风洞阻塞率的要求,将模型的几何缩尺比设为1∶200。模型主要采用ABS塑料板制成,图 1为安装在风洞内的试验模型。
 |
| 图 1 风洞试验模型 Fig. 1 Test model in wind tunnel |
由于本航站楼的建筑造型比较复杂,为了更详细地了解航站楼的风荷载特性,本次试验在航站楼模型上总共布置了948个测点(包括其屋盖和侧面),并在重点部位如大悬臂挑檐、天井以及悬空屋盖等部位进行了适当的加密处理,重点部位的典型测点布置图如图 2所示。值得说明的是,图中只标示了挑檐部位和悬空屋盖处的上表面典型测点S1-S8,对应下表面相同位置处的测点X1-X8则没有标示。
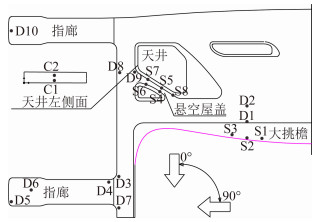 |
| 图 2 典型测点布置图 Fig. 2 Layout of selected taps |
根据最新版的建筑结构荷载规范,本航站楼所处位置的大气边界层特性应按B类地表,即α=0.15进行流场模拟,脉动风谱则按照 Von karman谱进行模拟,如图 3和图 4所示。试验时,在模型前方未扰动区设置一根参考高度为20.5 cm的皮托管,相应的实际参考高度为41 m。试验风速为8 m/s,采样频率设为250 Hz,总共采样点数为6 000,即总的采样时间为24 s。按照相似准则,实际的采样频率约为5 Hz,采样时长约为30 min。试验时,每间隔15°设置一个试验风向,按照顺时针方向旋转,如 图 2所示,总共有24个工况。
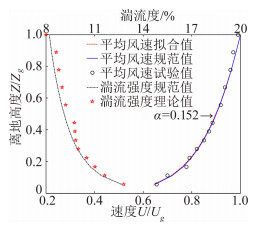 |
| 图 3 平均风剖面和湍流度剖面 Fig. 3 Profile of mean wind and turbulence intensity |
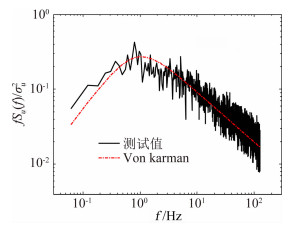 |
| 图 4 风洞实测与目标功率谱的对比 Fig. 4 Comparison of target and measured PSD in wind tunnel |
试验数据处理时,采取以下公式计算各测点的瞬时风压系数:
式中:Cpi(t)为模型各测压孔位置处的瞬时风压系数,pi(t)为该位置处的表面风压值,p0和p∞分别为参考点处的平均总压和平均静压。通过统计分析可得到各测点的平均风压系数和风压系数标准差。 2 结构的风荷载特性 2.1 典型工况的平均风压系数等值线图由于机场航站楼建筑外形比较复杂,因此,结构表面的风压分布也比较复杂。限于篇幅,本文选取90°和180°两个典型工况角下的屋盖平均风压特性进行详细阐述,图 5和图 6分别为两个工况角下的平均风压系数等值线图。
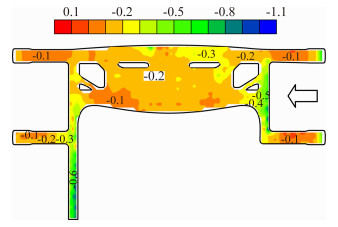 |
| 图 5 90°平均风压系数等值线图 Fig. 5 Contour map of mean wind pressure coefficient (90°) |
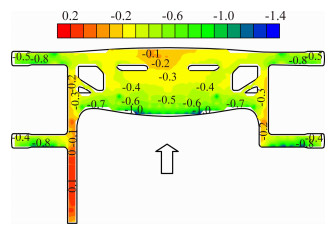 |
| 图 6 180°平均风压系数等值线图 Fig. 6 Contour map of mean wind pressure coefficient (180°) |
从图 5可以看出,在90°风向角下,屋盖以承受负压为主。右侧指廊部位及屋盖迎风区域的风压系数数值在-0.5左右,左侧连廊部位的风压系数则在-0.6左右。值得注意的是,除屋盖的迎风区域之外,其它很大一部分区域的风压系数极小,大致在-0.1附近徘徊。这是由于航站楼屋盖具有很明显的流线型,且跨越幅度很大,导致气流分离后的再附着区域很大,因此出现了风压系数极小的情况。在180°风向角下,屋盖同样以承受负压为主。大挑檐的平均风压系数大部分在-1.0附近,四个指廊迎风一侧的平均风压系数则在-0.8左右。而小挑檐及连廊部位的风压系数较小,其数值分别在-0.2和-0.1左右,其中连廊一部分再附着区域的平均风压系数为0.1左右。
2.2 重点部位的风压分布特性从建筑外形来看,本航站楼的大悬挑结构、天井以及悬空屋盖等部位比较特殊。为此,本文从中挑选了一部分典型测点,进行重点部位的风压特性分析,典型测点布置图如图 2所示。
图 7为典型测点的平均风压系数随风向角的变化图。从图中可以看出,在所有工况下,挑檐S1-S3测点的平均风压系数全部为负值。随着风向角的变化,所有挑檐上表面测点的平均风压系数都具有类似的变化规律,即吸力分别在90°、180°和270°附近达到极小值、极大值和极小值。其中,S2的平均风压系数在180°达到最不利,其数值为-1.58。从挑檐下表面测点X1-X3的平均风压系数图可以看出,随着风向角的不断增大,所有典型测点同样都具有平均风压系数不断增大,然后再递减的类似规律,且基本上都经历了由吸力到压力再到吸力的过程。在180°工况下,X2的平均风压系数最大,其值可达0.49。值得说明的是,挑檐在迎风作用时,上表面测点受到很大的吸力,下表面测点则同时受到较大的压力,上吸下压会使挑檐部位实际受到的风荷载明显增大。
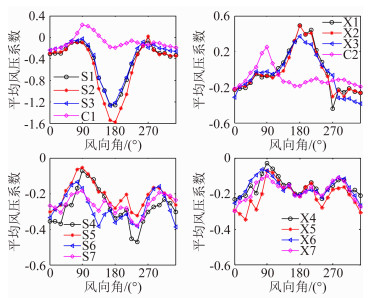 |
| 图 7 典型测点的平均风压系数图 Fig. 7 Mean wind pressure coefficient of selected taps |
从天井左侧侧面C1和C2典型测点的平均风压系数图可以看出,天井侧面典型测点的平均风压系数波动范围为-0.3~0.3之间,数值偏小,这与荷载规范规定的封闭式建筑物应考虑±0.2的内压比较吻合。其原因在于天井洞口的朝向为竖直方向,而不是侧面方向,因此,整个航站楼都可以近似看成为封闭式建筑物。
S4-S7和X4-X7测点分别为悬空屋盖处的上下表面典型测点。从图中可以看出,这些测点的平均风压系数都为负值,数值范围大致为-0.4~0,且上下表面测点的风压随风向角变化的规律基本一致。因此,悬空屋盖实际受到的平均风压会由于上下表面同时受到吸力而大大减小。
2.3 屋盖的高斯与非高斯分区众所周知,目前规范规定的主体和围护结构极值压力的计算都是以风压服从高斯分布为前提的,而对于大跨屋盖迎风和拐角等气流分离和涡旋很明显的区域,其风压分布具有明显的非高斯特性。因此,为了更好的进行结构抗风设计,有必要对屋盖进行高斯与非高斯分区。
目前,基于风压系数3阶和4阶统计量的高斯与非高斯分区方法已得到了广泛的应用,其原理可参考相关的文献[14, 15],限于篇幅,本文不再赘述。该方法的重点则是确定高斯与非高斯分区的评判标准。表 1列出了相关文献中,非高斯分区的风压系数偏度和峰态界限值。从表中可以看出,不同结构形式的非高斯分区划分标准存在一定的差异。参考大跨平屋盖[5]和大跨屋盖[6]的评判标准,并结合本航站楼的风压非高斯分布特性,本文将大跨屋盖的非高斯分区划分标准确定为|Csk|>0.4且|Cku|>3.5。值得一提的是,大跨屋盖的风压系数非高斯特性主要是由于气流分离、涡旋造成的负压脉冲引起的,该类风压系数的峰态大于3.0,为“softening”过程(峰值因子大于高斯过程)。
表 2为典型测点在180°、225°和270°下的风压系数3阶和4阶统计量。从表中可以看出,由于D2和D6在对应风向角下位于再附着区域,因此,这些测点的偏度和峰态都分别接近于0和3。而类似于S2和D7这些在对应风向角下处于气流分离区域的测点,其偏度和峰态的绝对值都明显高于非高斯分区的界限值,说明该类测点的风压非高斯特性极其明显。
| 角度 | 测点 | Csk | Cku | 区域 |
| 180° | S2 | -0.760 | 4.079 | NG |
| 180° | D1 | -0.377 | 3.934 | G |
| 180° | D2 | -0.035 | 3.051 | G |
| 225° | D10 | -0.548 | 3.589 | NG |
| 225° | D5 | -0.247 | 3.261 | G |
| 225° | D6 | -0.107 | 3.042 | G |
| 225° | D7 | -0.790 | 4.465 | NG |
| 270° | D8 | -0.417 | 3.548 | NG |
| 270° | D9 | -0.029 | 2.904 | G |
| 270° | D10 | -0.496 | 3.464 | G |
| 270° | D3 | -0.662 | 4.188 | NG |
| 270° | D4 | -0.883 | 4.767 | NG |
限于篇幅,且考虑到对称风向角的因素,本文只列出180°、225°和270°风向角下的偏度和峰态等值线图,如图 8~图 10所示。为了更加清晰的表达出高斯与非高斯分区,本文以非高斯划分标准为界限,采用红和黄两种颜色表示等值线图,黄色代表满足非高斯分区的条件,红色则代表不满足条件。因此,偏度和峰态等值线图重叠的黄色区域即为屋盖的非高斯区域。
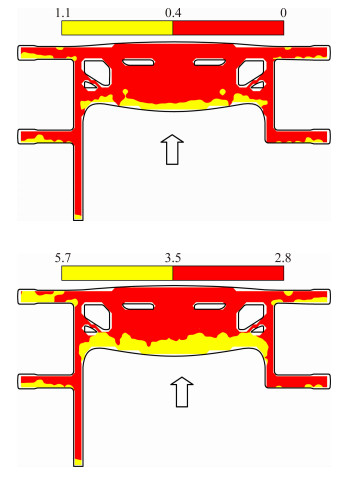 |
| 图 8 180°风向角下屋盖的偏度和峰态等值线图 Fig. 8 Contour maps of skewness and kurtosis of roof(180°) |
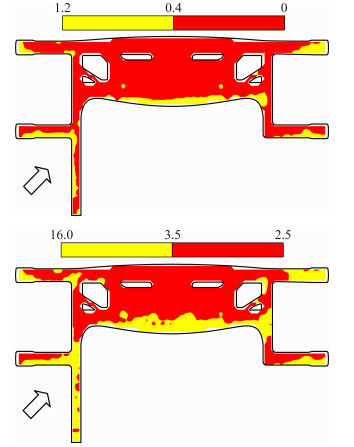 |
| 图 9 225°风向角下屋盖的偏度和峰态等值线图 Fig. 9 Contour maps of skewness and kurtosis of roof(225°) |
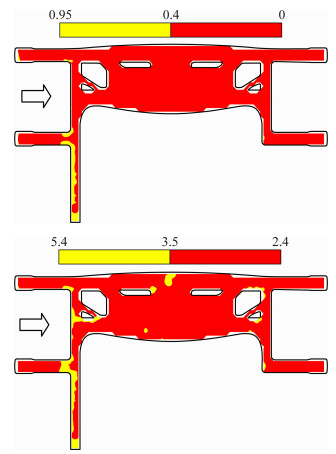 |
| 图 10 270°风向角下屋盖的偏度和峰态等值线图 Fig. 10 Contour maps of skewness and kurtosis of roof(270°) |
在180°风向角下,屋盖的非高斯区域主要集中在流动分离的挑檐位置以及第二排指廊的位置,区域范围基本上跨越了整个悬挑区域和1/2的指廊屋盖区域。值得说明的是,在第一排指廊与主体结构的拐角区域,同样存在着较为明显的非高斯特性。在225°风向角的作用下,屋盖的非高斯区域分布较为广泛,基本上所有的迎风区域都是非高斯区域,尤其是在连廊部位。在右侧第二排指廊与主体结构相连的拐角区域并没有出现非高斯分布现象,分析原因是在225°风向角时,该位置正好被旧航站楼给遮挡住。
与180°和225°风向角相比,270°风向角作用下的非高斯区域分布主要局限在连廊的迎风侧以及连廊与指廊的拐角位置。值得说明的是,在这三个工况下,天井部位都没有出现明显的非高斯风压分布现象。
3 悬空屋盖的局部风振响应分析 3.1 风振响应分析与风振系数通过风洞试验,获取测点的风压系数时程以后,则可以通过转化得到航站楼模型节点的风压力时程,随后则可以进行风振响应分析。风振分析主要有频域和时域两种计算方法,本文采用时域分析方法。其结构动力学方程如下:
式中,[M]、[C]、[K]分别为结构的质量矩阵、阻尼矩阵以及刚度矩阵;{ÿ}、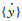 、{y}分别为结构的加速度、速度以及位移向量;{Pt}为作用在结构上的风荷载向量。相应的,结构增量的动力方程为:
其中,
、{y}分别为结构的加速度、速度以及位移向量;{Pt}为作用在结构上的风荷载向量。相应的,结构增量的动力方程为:
其中,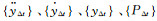 分别为结构的加速度、速度、位移以及风荷载增量向量。阻尼矩阵[C]采用瑞利阻尼,即其可表示为质量矩阵和刚度矩阵的线性组合,组合参数由结构的前两阶模态频率确定。
分别为结构的加速度、速度、位移以及风荷载增量向量。阻尼矩阵[C]采用瑞利阻尼,即其可表示为质量矩阵和刚度矩阵的线性组合,组合参数由结构的前两阶模态频率确定。
在计算时,采用Newmark时程分析方法。为使计算误差不至于累积而影响计算精度,可采取合适的时间增量,必要时可引入平衡迭代算法。
大跨屋盖的等效静风荷载问题仍然是现今没有完全解决的难题,虽然通过风振系数确定等效静风荷载的方法存在一定的误差,但其仍然是目前工程实践中应用比较多的方法。位移风振系数的定义如下:
式中:βdi为节点的位移风振系数;Rdi和Rsi分别为节点的动位移和静位移;μ为峰值因子,σdi为节点动位移响应的均方根值。本航站楼在采用上述方法计算位移风振系数时,悬空屋盖区域的风振系数数值过大,为了更加深入了解悬空屋盖的动力特性,保证结构的抗风安全,本文建立了悬空屋盖的局部分析模型,并对该区域在90°风向角下的风振响应进行了局部响应分析。
3.2 局部分析模型的建立局部分析模型建立的原则是突出悬空屋盖的振动特性,并且能适当考虑模型边界对悬空屋盖的影响,因此本文选取了整个天井区域的屋盖部分作为分析模型,钢屋盖的支撑选取了绕天井一圈的钢管支柱,选取的局部分析模型如图 11所示。
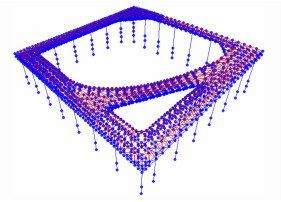 |
| 图 11 局部分析计算模型 Fig. 11 Local analysis model |
为使悬空屋盖在局部分析模型中的振动特性尽可能接近其在整体模型中的振动特性,局部分析模型的刚度应和该模型在整体模型中的刚度等效。为此,除了在钢支柱上的底部节点施加固定约束之外,还在屋盖边界节点以及钢支柱上的框架节点上设置了弹簧约束,以模拟整体模型中其它部分对局部模型部分刚度的影响。弹簧约束选取的是非耦合弹簧约束,约束刚度的计算模型如图 12所示。采用等效刚度的原则计算弹簧的6个约束刚度,即在弹簧刚度计算模型的边界节点上分别施加单位力,得出相应的节点位移,从而确定局部模型边界节点的弹簧刚度。最后,对节点弹簧刚度进行适当修正,以使悬空屋盖在局部模型中的振动模态接近其在整体模型中的振动模态。
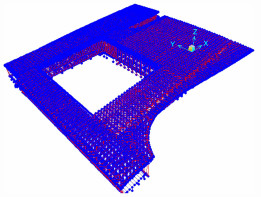 |
| 图 12 边界节点弹簧刚度计算模型 Fig. 12 Analysis model of spring stiffness on boundary node |
表 3为局部模型与整体模型的悬空屋盖局部振型的对比。从表中可以看出,两种模型的悬空屋盖振动模态非常吻合。如局部模型第1阶和整体模型第3阶的振动模态都为悬空屋盖竖向振动,振动频率则分别为1.224和1.249 Hz,两者之间吻合很好。
| 局部模型 | 整体模型 | 局部模型 | 整体模型 | |
| 阶数 | 第1阶 | 第3阶 | 第2阶 | 第17阶 |
| 频率 | 1.224 | 1.249 | 2.432 | 2.591 |
| 模态 | 悬空屋盖竖向振动 | 悬空屋盖反对称振动 | ||
除了刚度之外,为了使局部分析模型的阻尼特性与悬空屋盖在整体模型中的阻尼特性相似,局部分析模型选用的阻尼为瑞利阻尼,阻尼系数则选取整体模型中的阻尼系数。
3.3 局部分析模型风振系数计算将90°工况下,局部分析模型屋盖上下表面的测点风压系数时程通过模型节点加入到局部分析模型中,得出测点周围节点的位移风振系数,进而求出测点及分区的位移风振系数。
图 13为整体模型与局部分析模型中测点S4-S8周围节点的位移标准差对比图。从图中可以看出,两种模型的计算结果吻合非常好,这也说明本文建立的局部分析模型比较合理。对于悬空屋盖处节点的平均位移而言,两种模型的计算结果稍有偏差。这主要是由于从整体而言,局部分析模型的刚度要小于整体模型的刚度。此外,局部模型边界节点的加载也在一定程度上影响了局部模型的平均位移计算结果。对比局部模型和整体模型的测点和分区风振系数,可以发现两种模型的计算结果都较大,部分值达到20左右。同时两个模型部分测点风振系数的相对误差在20%左右,而分区风振系数的相对误差则为8%。由此可见,局部模型的风振系数计算结果与整体模型比较吻合。值得说明的是,两种模型下的节点位移标准差大都在14 mm附近波动,从数值上来看并不算大,而悬空屋盖节点由于上下表面同时受到吸力导致平均位移大都在1.5 mm附近波动。因此,可以认为,悬空屋盖处位移风振系数过大的主要原因是悬空屋盖的平均位移过小,这也是位移风振系数计算方法的缺陷之一。
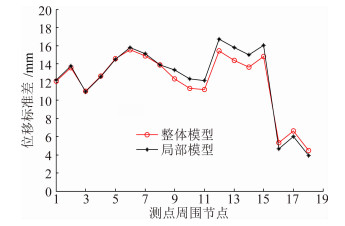 |
| 图 13 悬空屋盖处节点的位移标准差对比 Fig. 13 Comparison of displacement standard deviation of the nodes on suspended roof |
本文基于某机场航站楼的刚性模型风洞试验,对该航站楼的整体风压分布特性、重点部位的风压分布以及航站楼屋盖的非高斯风压分布特性进行了研究。此外,本文还对风振响应较大的悬空屋盖区域进行了局部模型风振响应分析,得出了以下几个结论:
(1) 在90°风向角下,右侧主体结构迎风区域的平均风压系数在-0.5左右,屋盖其它再附着区域的平均风压系数极小,其原因是航站楼跨越幅度大,且航站楼屋盖具有明显的流线型。在180°风向角下,大挑檐和指廊迎风侧的平均风压系数分别在-1.0和-0.8左右。大挑檐上表面平均风压系数最不利值为-1.58,下表面则为0.49,上吸下压会使挑檐实际受到的风荷载明显增大。
(2) 天井内部的风压特性与荷载规范规定的建筑物内压相吻合,悬空屋盖的平均风压则由于上下表面同时受到吸力而大大减小。
(3) 结合相关文献及本航站楼的实测结果,确定了航站楼屋盖非高斯分区的划分标准为 Csk >0.4且 Cku >3.5。从分区的结果来看,屋盖非高斯区域主要集中在屋盖边缘的迎风和拐角区域。值得一提的是,本航站楼的天井并没有出现明显的非高斯风压分布现象。
(4) 从悬空屋盖局部分析模型的计算结果来看,测点和分区位移风振系数的计算结果与整体模型比较吻合。悬空屋盖区域位移风振系数过大的主要原因是悬空屋盖区域平均位移过小。因此,可以认为悬空屋盖区域的风振响应是安全的。
| [1] | Zhou X Y, Gu M. Test study of wind pressure coefficient on long-span roof[J]. Journal of Tongji University, 2002, 30(2):1423-1428.(in Chinese) 周暄毅, 顾明. 大跨度屋盖表面风压系数的试验研究[J]. 同济大学学报, 2002, 30(2): 1423-1428. |
| [2] | Yu S C, Sun B N, Shen G H, et al. Experimental investigation of wind loads on umbrella-shaped membrane assembled roofs[J]. Acta Aerodynamic Sinica, 2005, 23(1): 40-45. (in Chinese) 余世策, 孙炳楠, 沈国辉, 等. 伞形膜结构组合屋盖风荷载特性的风洞试验研究[J]. 空气动力学学报, 2005, 23(1): 40-45. |
| [3] | Li Y Q, Hu W X, Wang L. State-of-art: wind tunnel investigation on wind pressure distribution of large-span spatial structures with typical shapes[J]. Acta Aerodynamic Sinica, 2010, 28(1): 32-38. (in Chinese) 李元齐, 胡渭雄, 王磊. 大跨度空间结构典型形体风压分布风洞试验研究现状[J]. 空气动力学学报, 2010, 28(1): 32-38. |
| [4] | Wu D, Wu Y, Sun Y, et al. Wind tunnel test and equivalent static wind loads on large span station buildings[J]. Journal of Building Structures, 2012, 33(1): 43-50. (in Chinese) 吴迪, 武岳, 孙瑛, 等. 大跨度铁路站房屋盖结构风洞试验与等效静风荷载研究[J]. 建筑结构学报, 2012, 33(1): 43-50. |
| [5] | Sun Y, Wu Y, Lin Z X, et al. Non-Gaussian features of fluctuating wind pressures on long span roofs[J]. China Civil Engineering Journal, 2007, 40(4): 1-5. (in Chinese) 孙瑛, 武岳, 林志兴, 等. 大跨屋盖结构风压脉动的非高斯特性[J]. 土木工程学报, 2007, 40(4): 1-5. |
| [6] | Ye J H, Hou X Z. Non-Gaussian features of fluctuating wind pressures on long span roofs[J]. Journal of Vibration and Shock, 2010, 29(7): 9-15. (in Chinese) 叶继红, 侯信真. 大跨屋盖脉动风压的非高斯特性研究[J]. 振动与冲击, 2010, 29(7): 9-15. |
| [7] | Kasperski M, Niemann H J.The LRC (load-response correlation) method: a general method of estimating unfavorable wind load distributions for linear and nonlinear structural behavior[J]. Journal of Wind Engineering and Industrial Aerodynamics,1992, 43(3): 1753-1763. |
| [8] | Holmes J D. Effective static load distributions in wind engineering[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(2): 91-109. |
| [9] | Huang G Q, Chen X Z. Wind load effects and equivalent static wind loads of tall buildings based on synchronous Pressure Measurements[J]. Engineering Structures, 2007, 29(10): 2641-2653. |
| [10] | Lu F, Lou W J, Sun B N. Wind-induced dynamic response and wind load factor for long-span flat roof structures[J]. Engineering Mechanics, 2002, 19(2): 52-57. (in Chinese) 陆锋, 楼文娟, 孙炳楠. 大跨度平屋面的风振响应及风振系数[J]. 工程力学, 2002, 19(2): 52-57. |
| [11] | Li Q X, Lou W J, Yang S C, et al. Wind load factor and parametric analysis of long-span single-layer spherical reticulated shell[J]. Journal of Building Structures, 2006, 27(4): 65-72. (in Chinese) 李庆祥, 楼文娟, 杨仕超, 等. 大跨单层球面网壳的风振系数及其参数分析[J]. 建筑结构学报, 2006, 27(4): 65-72. |
| [12] | Tian Y J, Yang Q S, Fan C, et al. Gust factors for large-span roof of the national stadium[J]. Journal of Building Structures, 2007, 28(2): 26-31. (in Chinese) 田玉基, 杨庆山, 范重, 等. 国家体育场大跨度屋盖结构风振系数研究[J]. 建筑结构学报, 2007, 28(2): 26-31. |
| [13] | Pan F, Ye Y, Sun B N. Three-dimensional numerical simulation of spatial-correlated stochastic wind field based on double POD model[J]. Acta Aerodynamic Sinica, 2009, 27(1): 129-135.(in Chinese) 潘峰, 叶尹, 孙炳楠. 基于双POD模型的大跨屋盖多模态随机风致响应研究[J]. 空气动力学学报, 2009, 27(1): 129-135. |
| [14] | Kumar K S, Stathopoulos T. Wind loads on low building roofs: a stochastic perspective[J]. Journal of Structural Engineering, 2000, 126(8): 944-956. |
| [15] | Lou W J, Li J X, Shen G H, et al. Non-Gaussian feature of wind-induced pressure on super-tall building[J]. Journal of Zhejiang University(Engineering Science), 2011, 45(4): 671-677. (in Chinese) 楼文娟, 李进晓, 沈国辉, 等. 超高层建筑脉动风压的非高斯特性[J]. 浙江大学学报(工学版), 2011, 45(4): 671-677. |