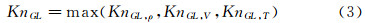2. 中国航天空气动力技术研究院, 北京 100074
2. China Academy of Aerospace Aerodynamics Technology, Beijing 100074, China
0 引 言
随着航天技术的不断发展,各类飞行器在过渡流域范围内工作的时间越来越长,其飞行过程中的运动特性逐渐成为研究的热点。根据Knudsen数(克努森数)的不同,将飞行器所经历的流场分为连续流区、过渡流区和自由分子流区,这其中过渡流区的求解问题最为复杂。这是因为航天飞行器在过渡流区飞行时,不仅流场大部分区域或局部区域内存在着明显的稀薄气体效应,而且由于压缩效应甚者可能出现连续流与稀薄流共存的混合流场,从而使整个流场具有连续与稀薄流混合的特性。过渡流区飞行器绕流特性问题一直是高超声气动技术的难点和热点。
在过渡流区,连续介质模型开始失效,基于N-S方程 的CFD(Computational Fluid Dynamics)方法不再适用,而稀薄气体动力学方法则成为该流域的主要研究方法。这其中Bird提出的DSMC(Direct Simulation of Monte Carlo)方法 得到了广泛的运用[1]。针对连续与稀薄流动共存的混合流场,则需采用基于连续流和稀薄流的CFD/DSMC耦合方法进行计算[2, 3, 4, 5, 6]。该方法针对不同的区域采用相应的算法进行计算,既可以完整地反应混合流场的特征,又尽可能地提高了计算效率。在此方面,Hash和Hassan提出了一种CFD/DSMC的解耦方法,并尝试采用基于通量的弱耦合方法模拟了Couette流动[7];T.E. Schwartzentruber和I.D. Boyd对CFD/DSMC耦合方法进行了完善和扩充,以局部Knudsen数对混合流场进行划分,采用基于状态参数的方法对高超声速非平衡气体流场进行模拟,并提出一种“亚松弛”方法降低统计耗散[8]。李中华等在此基础上发展了适用于流场分区信息交换的亚松弛技术,对CFD/DSMC耦合算法在低克努森数流场中的应用进行了研究[9]。尽管只采用了单一的网格结构,但这些研究仍为耦合方法的发展提供了完整的思路。另外在网格方法上,梁杰等以笛卡尔网格DSMC方法为基础,引入了自适应的非结构网格方法,为重叠网格方法在稀薄气体中的应用提供了参考[10]。
在混合方法中,由于不同流区计算方法不同,其分界面的划定则成为了该方法要解决的首要问题。在连续/稀薄流混合流场中,很多情况下并没有明确的界面将流场区分开来,因此在初始流场中稀薄与连续区域的交界面位置都是未知的,需要采用连续介质失效参数进行判定。而在流场推进中,取某一时刻的计算结果进行划定的流场区域并不一定符合流场最终的情况,因此需要采用自适应方法进行推进,并采用CFD/DSMC耦合方法进行流场计算。连续流区采用的CFD方法和稀薄流区采用的DSMC方法对计算网格的类型、质量、尺度的要求不同,因此采用单一类型的计算网格难以兼顾不同求解方法的特点和要求,也难以得到较为精确可靠的数值解。此外两种流动界面的复杂性和推进过程界面的运动性,导致单一的网格类型也难以适应计算。为此,本文提出了一种基于结构和非结构网格的重叠网格界面自适应推进方法,开展了高超声速连续/稀薄流混合流场数值模拟技术研究,编制了通用的计算程序,通过对过渡流域超声速圆柱绕流和高超声速带扩张角圆管绕流的数值试验,验证了算法的可行性与有效性。
1 连续/稀薄混合流场数值模拟方法在连续流区域,本文采用基于结构网格N-S方程的CFD算法,以获得高精度的计算结果和流场分辨率;在稀薄流区域,采用非结构网格DSMC方法进行计算。
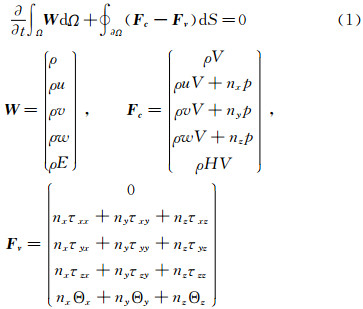
1.1 连续流区数值求解方法直角坐标系中积分形式的N-S方程为
其中,W 为守恒变量,Fc 为无粘通量,Fv 粘性通量。对于每一个控制体单元,采用有限体积法对方程进行离散,对流通量离散采用Van Leer矢通量分量格式,并使用Van Albada限制器通过MUSCL方法进行插值。粘性项采用中心差分离散,时间推进采用五步Runge-Kutta法。连续流区CFD方法一般利用正交性较强的结构网格以取得较高精度的解,所用的网格尺度依赖于解算格式和流场的宏观特性,是基于宏观层面流场特性的宏观网格尺度。本文在连续流区中采用结构化网格。由于不同流区之间需要通过单元信息量的插值进行数值传递,因此结构网格单元需要在模拟流场宏观变化的同时满足微观分子运动规律和统计规律,使不同区域间的流场能够光滑过渡。该网格既需要能够在插值处模拟出微观流动变化的情况(尺寸在分子平均自由程左右),又需要包含有足够多的分子以满足稀薄区域中相关单元的统计需求(至少20个分子),同时需要能够模拟近壁面处的粘性效应。据此,本文以来流气体分子平均自由程的0.1倍至0.33倍为标准设定结构网格单元在近壁面处的尺寸,使其满足不同区域间网格的匹配需求。
1.2 稀薄流区非结构网格DSMC方法在稀薄流区采用基于微观分子气体动力学的DSMC方法。DSMC方法用有限个模拟分子代替真实气体分子,在计算机中存储模拟分子的位置坐标、速度分量以及内能,其值随模拟分子的运动与边界的作用以及模拟分子之间的碰撞而不断变化,通过对计算网格内模拟分子的运动状态取样统计达到求解真实气体流动的目的。DSMC方法对网格类型依赖程度较小,但对网格尺度要求较高,该方法中网格的作用主要是对流场进行分子微观取样和统计。网格尺度过大和过小均得不到正确的计算结果,过大的尺度会导致计算精度的降低,而过小的尺寸会导致统计涨落过于明显。因此,DSMC方法中计算网格尺度取决于流场的稀薄程度,是基于流场微观层面上稀薄程度的微尺度网格。一般来说,在生成初始网格时,以来流气体平均分子自由程的三分之一为标准确定网格单元的大小,这样可以保证贴近物面的高密度区的计算精度,同时由于近壁面处分子数密度大,可以保证该尺寸单元在取样时有足够的分子样本。本文DSMC计算网格采用对复杂外形适应性较强和求解过程易于加密的非结构网格[11, 12],以保证对复杂流域的高度适应性和DSMC方法对网格尺度的要求。
为了解决传统DSMC方法统计涨落对CFD/DSMC耦合计算的影响,本文采用基于信息保存IP方法[13]的DSMC方法。分子模型采用GSS-3模型[14],该模型同时具有吸引和排斥的分子作用力,能够给出正确的气体输运性质。利用分子与相邻单元面的相交理论设计追踪模拟分子在网格间迁移运动的搜索算法,同时引入碰撞距离的思想来保证正确的模拟结果。
2 自适应推进界面中的连续失效参数连续与稀薄流混合流场的计算中,分界面的划分通常采用一个连续介质失效参数作为判定依据,并根据实际情况给出截止值,将不同流场部分中连续失效参数值与截止值进行比较,大于截止值的部分采用DSMC方法,反之则采用CFD方法,这两部分的分界面则是CFD/DSMC的交界面。本文采用Boyd提出的局部克努森数法[15, 16]作为界面划分的依据:
其中,λ是分子平均自由程,Q表示某流动参数,例如密度,速度或者温度。通常采用这些局部克努森数的最大值作为具体计算中的失效参数,即: 在计算中连续介质失效参数的截止值取为0.05。 3 自适应界面推进中的重叠网格方法 3.1 主要思想本文发展的连续/稀薄流混合流场重叠网格法的基本思想是根据不同流区对计算网格的需要,用两套独立生成的不同尺度网格覆盖整个流场,在不同的流动区域形成重叠网格。不同流区的多尺度计算网格一次生成,两套网格可根据需要实现任意不同类型和尺度网格的重叠、杂交和重叠区域任意形式的动态改变。根据连续/稀薄流界面失效函数的截止值在连续流区进行自适应“挖洞”,动态改变两套网格的重叠部分,挖洞后的区域为DSMC区域,并激活DSMC区域的非结构网格利用DSMC方法进行计算。同时根据自适应过程,对于不再参与稀薄流区计算的非结构网格单元进行“休眠”,并激活相应位置的结构网格单元参与连续流区的计算。在连续/稀薄流区分界面附近的重叠区域利用插值方法实现流场信息的传递。
3.2 重叠网格技术中的区域挖洞方法由于结构网格和非结构网格单元均是独立覆盖全流场的,二者数据结构完全不同,当根据失效参数的截止值以结构网格进行区域洞边界划分时,如何确定非结构网格的点是否落在洞内成为了该方法的关键。
由于非结构网格的拓扑结构的无序性,本文以结构网格为背景网格发展了一种区域挖洞方法,其一般过程为:
(1) 首先以结构网格作为背景网格,遍历所有非结构网格单元,利用其形心坐标找出并记录所属的结构网格单元,将结构网格单元和非结构网格单元建立起对应关系,即确定结构网格单元与非结构网格单元的包含关系。
(2) 当进行重叠网格洞边界划分时,以流场计算的结构网格为基础进行洞边界划分,通过网格点上的局部克努森数的大小将点分为计算点(激活状态)与非计算点(休眠状态),将与非计算点相邻的计算点设置为边界点,根据单元形心点的属性将单元分为计算单元与非计算单元,并从计算单元的边界处起,感染相邻的非计算单元作为插值单元。此时初始洞边界已完成。
(3) 遍历结构网格所有洞内(DSMC区域)和洞外单元(CFD区域),分别将所有包含在内的非结构网格点相应的设置为计算点(激活状态)和非计算点(休眠)。再检查非结构网格中的所有单元,根据单元中所有点的具体属性(计算点、非计算点和界面点)将其设置为洞内单元,洞外单元和插值单元。
(4) 遍历所有网格单元,根据结构和非结构网格单元属性给出CFD和DSMC计算区域,如图 1所示。
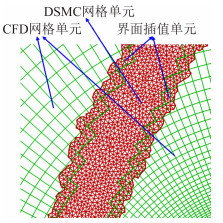 |
| 图 1 挖洞后CFD/DSMC计算网格单元 Fig. 1 Overlapping grid of CFD/DSMC after hole cutting |
在计算中,DSMC和CFD区域的信息传递通过插值单元处的信息转换完成。由于DSMC的计算结果为统计量,在信息转换时不可避免的存在统计耗散,本文采用IP方法对其进行改进,有效地抑制了DSMC统计涨落对CFD的影响。根据CFD/DSMC方法交界面两侧的信息传递方式,可将耦合方法分为两种:基于通量法和基于状态参数法。基于通量法依赖于大量的分子统计,在分子数不足的情况下可能会发生计算崩溃的情况,因此本文采用基于状态参数法进行计算。
状态参数法首先对洞边界两侧不同区域单元内的状态参数进行转换,生成洞边界外侧单元的信息值,然后使用该值进行流场计算。但在结构与非结构网格互相重叠的情况下,不同区域的洞边界面并不重合,因此首先需要根据各区域的洞边界位置确定其外侧单元,然后以该单元在相邻区域中的贡献单元信息为基础进行插值,最后将计算出的单元信息转换为洞边界上各计算方法所需要的物理量。这样使得各区域在处理洞边界的通量信息时,外侧单元与计算单元之间的界面相互重合,从而保证了该区域内的通量守恒。
当CFD区域为DSMC区域提供边界条件时,即重叠区数值需要进行从宏观量到微观量的转换,此时连续流区的宏 观参数为信息源,其信息交换过程如下:
(1) 确定在连续流重叠区的非结构网格单元,标记需要进行信息重置的网格。
(2) 对所有被标记到的非结构网格单元进行信息重置,将该单元内分子的速度,温度,位置等信息归零,删除分子链表中相关信息。
(3) 对重叠区中相关结构网格单元进行信息转换处理,即以结构网格单元内的密度,速度,温度等宏观信息量为基础,用Chapman-Enskog理论方法生成结构网格单元内的分子信息。
(4) 在结构网格单元内对分子位置进行随机分布,将生成的新分子纳入到所对应非结构网格单元的分子信息链表中。
重叠区内当DSMC区域向CFD区域提供边界条件时,即重叠区数值需要进行从微观量到宏观量的转换,此时稀薄流区的微观参数为信息源,信息交换过程如下:
(1) 对重叠区中相关结构网格单元内的宏观量进行重置,并根据单元间的关系链表确定与其相关的非结构网格单元编号。
(2) 对每个结构网格单元,首先统计该单元的所有相关非结构网格单元。然后分别求出各相关非结构网格单元中心到该单元中心的距离,将该值的倒数作为加权系数,按照如下公式计算:
式中,L为距离的倒数,Qi为信息量。求出Q值之后,将其作为插值单元中的信息值进行通量计算。(3) 按上述方法整理所有结构网格单元中新生成的宏观量,将其赋值给相关的结构网格单元。
4 连续/稀薄流自适应界面算法流程本文所设计的连续/稀薄流自适应界面推进重叠网格算法的主要流程如下:
(1) 采用结构网格和非结构网格分别布置全流场,并采用结构网格CFD方法进行流场初始计算,以迭代Nstep步后的流场作为耦合开始计算的初始流场。
(2) 采用局部克努森数作为稀薄与连续流区域划分的标准,其截止值取0.05,在结构网格内划出初始的洞边界。
(3) 以结构网格初始洞边界为基准,在非结构网格内进行挖洞,划出相应的DSMC计算、插值和非计算区域。
(4) 进行CFD和DSMC的耦合迭代计算,由于耦合迭代步数较小时界面移动不明显,为此本文在程序中设定自适应的循环迭代间隔数NADAP。
(5) 如果MOD(NPR,NADAP)=0进入自适应阶段,按照新计算的流场结果再次划定结构和非结构网格的洞边界区域,这里NPR为循环总数,NADAP自适应循环间隔数。
(6) 统计结构网格与非结构网格的洞边界情况,当上下两个自适应间隔时间步内的洞边界位置不再变化时,关闭自适应挖洞的过程,将该分界面作为最终分界面。按此界面耦合计算至收敛,否则返回(4)继续进行流场的自适应界面推进计算。
(7) 由于重叠网格的不同区域算法不同,因此其判定标准也不相同。NS方法一般以密度作为残差的标准,计算时首先记录所有单元两次时间步之间的密度相差值之和,将每一步的残差和与初始残差和相比,当该比值小于或者等于10-4时认为进入收敛状态;DSMC方法一般以统计涨落的情况作为判定收敛的标准,首先统计两个统计循环中分子总数的相差值,当该值与分子总数的统计平均值之比小于10-4时,认为计算已经收敛。在重叠网格耦合计算中,当这两个条件均满足时,认为流场计算收敛。
5 数值算例与分析 5.1 超声速圆柱绕流本文首先计算了超声速圆柱绕流来验证算法的有效性,计算模型来自文献[17],圆柱直径为0.1 m,采用结构和非结构网格覆盖全流场,非结构网格共由41 694个三角形单元和21 090个点组成;结构网格规模为50×100个计算单元。计算条件同文献[17],来流气体为纯氮气,粘性系数的温度幂指数为0.74,分子自由度为5,来流马赫数为4,速度为1 412.5 m/s,温度为300 K,圆柱壁面温度为500 K,密度为4.65×10-6 kg/m3。流场中分子数密度为1.0×1020,每个模拟分子所代表的真实分子数设为2.5×1013,时间步长为4.0×10-6s。
图 2给出了界面自适应过程中连续/稀薄流区计算网格单元变化情况,从图中可以看出随着流场的发展和激波的形成及移动,连续流区与稀薄流区逐渐发展的过程。在弓形激波和近壁面附近由于流场物理量梯度的急剧变化导致稀薄气体效应明显,生成了局部范围内的DSMC区域,并且随着弓形激波的发展,激波附近的DSMC区域逐渐扩展。在圆柱的尾流区,由于低密度效应生成了局部DSMC区域。从图中可以看出,尾流区的DSMC区域呈现先增大后减小的趋势,这主要是因为在流场初始计算时,尾部区域流场速度取为来流均匀速度,较大的初始速度造成计算过程中尾部区域首先出现大面积的稀薄流区,而后由于气流对尾部稀薄流域的气体补充作用,稀薄流区又逐渐减小。
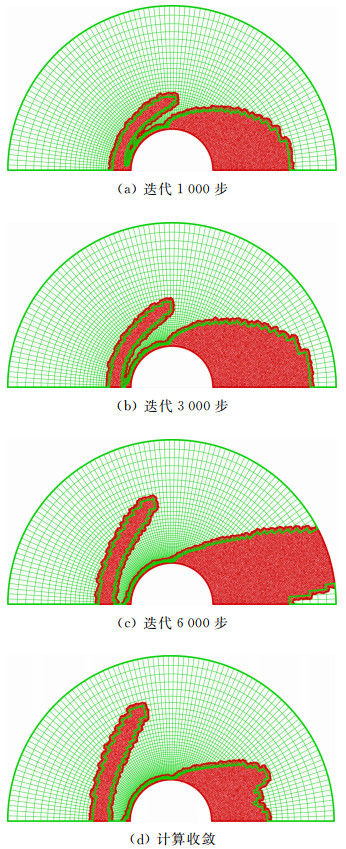 |
| 图 2 圆柱绕流连续/稀薄流区计算网格自适应界面推进过程 Fig. 2 Overlapping grids during adaptive interface advancement process of a cylinder supersonic flow |
图 3和图 4分别给出了圆柱绕流自适应界面推进过程中密度和温度的计算等值线图,并分别指出了等值线和不同区域分界面的位置。从图中可以看出,在流场的发展过程中,整个流场的分辨率较高,圆柱头部弓形激波发展过程中激波面清晰,这表明本文采用基于信息保存方法的DSMC方法有效抑制了统计涨落对CFD/DSMC耦合过程的影响。同时也表明在自适应推进过程中本文所使用的连续流CFD方法与稀薄流DSMC方法耦合边界处信息交换方法是可行的。
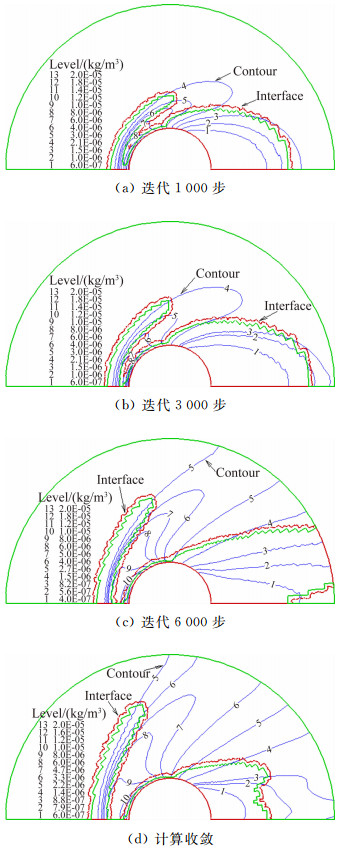 |
| 图 3 圆柱绕流连续/稀薄流区自适应界面推进过程密度计算等值线图 Fig. 3 Density contours of supersonic cylinder during adaptive interface advancement process |
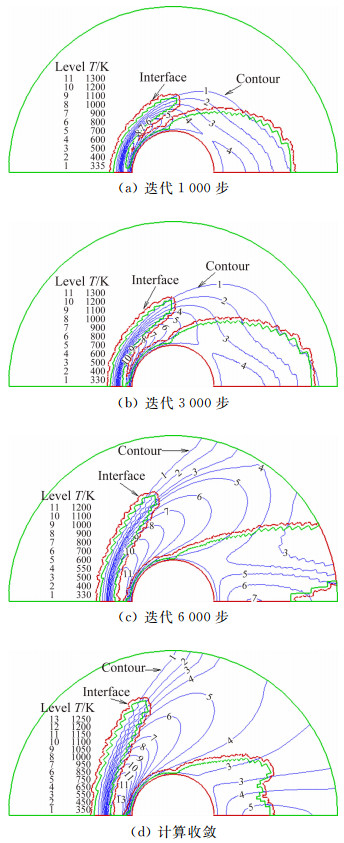 |
| 图 4 圆柱绕流连续/稀薄流区自适应界面推进过程温度计算等值线图 Fig. 4 Temperature contours of supersonic cylinder during adaptive interface advancement process |
图 5给出了圆柱绕流壁面气动系数计算结果比较,图中横坐标L为以驻点为起始点的弧长值,从图中可以看出本文计算结果与文献[17]以及DSMC计算结果吻合得较好,进一步表明本文发展的方法是可行的。图 5(a)为沿上壁面的压力系数分布,可以看出从驻点起压力系数分布类似于余弦函数曲线分布,与理论分析结果一致,图 5(b)给出从驻点沿上壁面的摩擦系数分布的计算比较,在驻点处摩擦系数为零,沿上壁面逐渐增加,在圆心角45°左右增加至最高峰后沿圆柱壁面又减小,与理论分析结果一致。
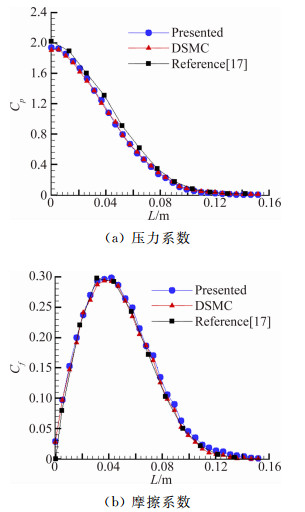 |
| 图 5 圆柱壁面物理量分布计算结果比较 Fig. 5 Comparison of calculated results on the cylinder wall |
带扩张角的圆管结构示意如图 6所示,计算区域为管外的流场,即圆管外壁与扩张角形成的组合体。采用结构和非结构网格覆盖全流场,非结构网格共由76 407个三角形单元和39 406个点组成;结构网格为由60×120个计算单元组成。
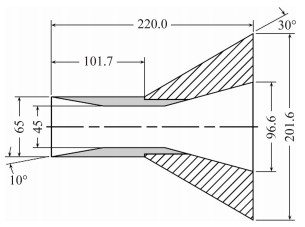 |
| 图 6 带有扩张角的圆管结构示意图 Fig. 6 The structure of the hollow cylinder-flare |
计算条件同文献[18],来流气体为纯氮气,粘性系数的温度幂指数为0.74,分子自由度为5,来流马赫数为10.5,速度为2 301.7 m/s,温度为118.2 K,密度为9.023×10-4 kg/m3。分子数密度为1.94×1022,每个模拟分子所代表的真实分子数设为3.5×1014,时间步长为2.0×10-6s。
图 7给出了自适应界面推进完成后连续流区与稀薄流区计算网格及密度云图。从图 7(b)中可以看出,圆管壁面斜激波和扩张壁面斜激波的相互干扰特征明显,激波与激波同侧相交处密度增高,整个绕流显示了较高的流场分辨率,进一步说明了本文所设计的自适应方法是可行的。
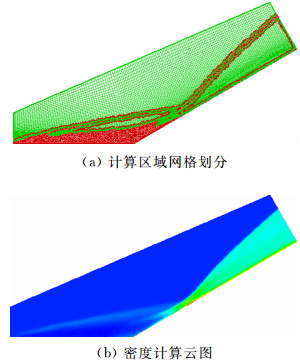 |
| 图 7 自适应过程完成后计算区域网格划分及密度云图 Fig. 7 Overlapping grid and density contours of after adaptive interface advancing process |
图 8给出了扩张圆管摩擦系数与壁面热流分布计算结果的比较,从图中可以看出本文摩擦系数和热流计算结果与文献[18]中给出的计算值与实验值吻合得较好。
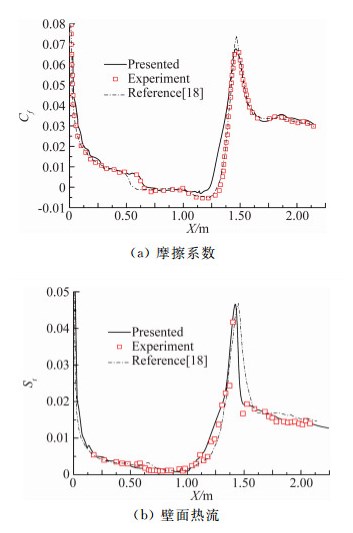 |
| 图 8 扩张圆管壁面物理量分布计算结果比较 Fig. 8 Comparison of calculated results on the wall of hollow cylinder-flare |
为了考察自适应界面推进重叠网格法的计算效率,本文将算例1与算例2在相同配置的计算机上分别利用非结构网格DSMC方法和本文方法进行了计算效率比较。所用计算机为曙光CB85-F四路四核高性能刀片计算服务器,CPU为AMD Opteron 8374HE,主频2.2 GHz,16 GB内存。表 1列出了每种方法从计算开始至收敛所用计算时间的比较,表 2列出了统计稳定后至收敛时的计算时间和各区域在总流场区域中所占的比例。从中可以看出与DSMC方法相比较,本文方法有效地减少了稀薄区域的计算量,降低了计算时间,提高了计算效率。
| 方法 | 算例1 | 算例2 |
| 本文计算时间/s | 2 320 | 3 240 |
| DSMC计算时间/s | 4 940 | 6 510 |
| 方法 | 算例1 | 算例2 |
| 耦合方法统计时间/s | 483 | 675 |
| DSMC方法统计时间/s | 920 | 1 102 |
| 连续区域所占比例 | 81.6% | 77.0% |
| 稀薄区域所占比例 | 18.4% | 23.0% |
为了比较两种算法的收敛历程,图 9给出了算例1中圆柱的阻力系数收敛变化曲线。从图中可以看出,与DSMC方法相比,本文方法不仅在计算速度上有明显的优势,并且阻力系数变化和收敛过程更加稳定,进一步表明了混合方法的优势。
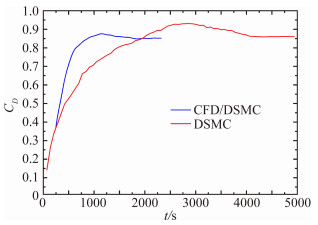 |
| 图 9 圆柱表面阻力系数的收敛过程 Fig. 9 The convergent process of the drag coefficients on the cylindrical surface |
本文开展了过渡流区高超声速连续/稀薄流混合流场数值模拟技术研究。提出了一种基于结构和非结构网格基础上的重叠网格界面自适应推进方法。通过超声速圆柱绕流和高超声速扩张圆管绕流的数值模拟验证,可以得到如下结论:
(1) 数值计算结果表明该方法在处理连续/稀薄流混合流场的模拟问题是可行的,所得流场分辨率高,计算结果与文献和实验比较吻合较好。
(2) 该方法在求解过程中可以自适应捕捉连续流与稀薄流的分界面,实现了界面捕捉和耦合计算过程的统一。
(3) 通过计算效率的比较,该方法与非结构网格DSMC方法相比,能够有效降低计算时间,提高计算效率。
| [1] | Bird G A. Molecular gas dynamics and the direct simulation of gas flows[M].Oxford: Clarendon Press, 1994. |
| [2] | Thomas E S, Leonardo C S, et al. Modular implementation of a hybrid DSMC-NS algorithm for hypersonic non-equilibrium flows[R]. AIAA 2007-613. |
| [3] | George J D, Boyd I D. Simulation of nozzle plume flows using a combined CFD/DSMC approach[R]. AIAA-99-3454, 1999. |
| [4] | Wadsworth D C, Erwin D A. Two-dimensional hybrid contiuum particle simulation approach for rarefied flows[R]. AIAA-92-2975, 1992. |
| [5] | Schwartzentruber T E, Scalabrin L C, Boyd I D. Hybrid particle continuum simulations of non-equilibrium hypersonic blunt body flow fields[R]. AIAA 2006-3602. |
| [6] | Li Zhihui, Li Zhonghua, et al. Coupled simulation of mixture plume for attitude control satellite thruster[J]. Acta Aerodynamica Sinica, 2012, 30(4): 483-491. (in Chinese) 李志辉, 李中华, 等. 卫星自控发动机混合物羽流场分区耦合计算研究[J]. 空气动力学学报, 2012, 30(4): 483-491. |
| [7] | Hash D B, Hassan H A. Assessment of schemes for coupling Monte Carlo and Navier-Stokes solution methods[J]. J. Thermophys Heat Transf., 1996, 10: 242-249. |
| [8] | Schwartzentruber T E, Boyd I D. A hybrid particle-continnum method applied to shock waves[J]. Journal of Computational Physics, 2006, 215: 402-416. |
| [9] | Li Zhonghua, Li Zhihui, Li Haiyan, et al. Research on CFD/DSMC hybrid numerical method in rarefied flows[J]. Acta Aerodynamica Sinica, 2013, 2013,31(3):282-287. (in Chinese) 李中华, 李志辉, 李海燕, 等. 过渡流区N-S/DSMC耦合计算研究[J]. 空气动力学学报, 2013, 31(3): 282-287. |
| [10] | Liang Jie, Yan Chao, Du Boqiang. An algorithm study of three-dimensional DSMC simulation based on two-level cartesian coordinates grid structure[J]. Acta Aerodynamica Sinica, 2010, 28(4):466-471.(in Chinese) 梁杰, 阎超, 杜波强. 基于两级直角网格结构的三维DSMC算法研究[J]. 空气动力学学报, 2010, 28(4): 466-471. |
| [11] | Wang Xuede, Wu Yizhao, Xia jian. Strategies for implement-tation of 2D unstructured DSMC method and its application[J]. Acta Aerodynamica Sinica, 2007, 25(1): 110-115. (in Chinese) 王学德, 伍贻兆, 夏健. 一类二维非结构网格DSMC方法实现策略及其应用[J]. 空气动力学学报, 2007, 25(1): 110-115. |
| [12] | Wang Xuede, Wu Yizhao, Xia jian. A parallel algorithm of 2D Unstructured DSMC method with dynamic load balance[J]. Acta Aerodynamica Sinica, 2007, 25(3): 339-344. (in Chinese) 王学德, 伍贻兆, 夏健. 动态负载平衡的二维非结构网格DSMC并行算法研究[J]. 空气动力学学报, 2007, 25(3): 339-344. |
| [13] | Sun Q H, Boyd I D. Theoretical development of the information preservation method for strongly nonequilibrium gas flows[C]//The 38th AIAA Thermophysics Conference,Toronto, Ontario, Canada, June 2005. |
| [14] | Wang Xuede, Wu Yizhao, Xia jian. GSS-3 molecular model in Monte Carlo simulation[J]. Chinese Journal of Computational Physics, 2009, 26(1): 64-70. (in Chinese) 王学德, 伍贻兆, 夏健. 蒙特卡罗方法中分子作用模型的设计及应用[J]. 计算物理, 2009, 26(1):64-70. |
| [15] | [KG0.85mm] Wang W L, Boyd I D. Continuum Breakdown in Hypersonic Viscous Flows[R]. AIAA 2002-0651. |
| [16] | Lofthouse A J, Boyd I D, Wright M J. Effects of continuum breakdown on hypersonic aerothermodynamics[R]. AIAA-06-0993, 2006. |
| [17] | 王学德. 高超声速稀薄气流非结构网格DSMC及并行算法研究[D]. 南京:南京航空航天大学, 2006. |
| [18] | Wang W L, Boyd I D. Hybrid DSMC-CFD simulations of hypersonic flow over sharp and blunted bodies[R]. AIAA 2003-3644. |