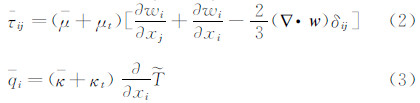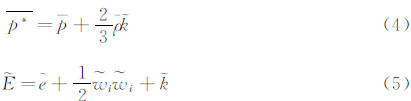0 引言
涡轮螺旋桨发动机具有耗油率低,效率高和低速飞行时推力大等特点,所以当前在战术运输机和低速中小型无人机上依然广泛采用螺旋桨推进。如欧洲空客A400运输机、美国C130“大力神”运输机和捕食者系列无人机(如图 1)[1, 2, 3],以及国产新舟60、运七、运八和运十二飞机等均采用涡桨发动机推进系统。螺旋桨飞机在研制过程中其气动设计必须要着重考虑螺旋桨滑流对全机的气动性能干扰。这种滑流干扰比涡轮喷气发动机的影响更加突出,甚至可以决定整个飞机设计的成败。因此,在研制初期开展螺旋桨滑流对飞机气动性能干扰影响的研究是非常重要的[4, 5]。螺旋桨飞机滑流影响的评估一直是螺旋桨飞机气动设计的难点之一。
 |
| 图 1 A400M、C-130战术运输机和捕食者无人机Fig. 1 A400M、C-130 tactical transport aircraft and Predator UAV |
对于螺旋桨产生的滑流流场,通常需要考虑流场的加速效应,旋转效应、粘性效应、湍流效应,桨盘倾斜的影响以及轴毂的影响[6]。国内外长期以来对螺旋桨滑流作了大量的研究工作,提出了一些简化的计算方法,主要有面元法[7, 8]、以动量理论为基础的等效盘模型(激励盘)[9, 10, 11]和螺旋桨数值模拟[12, 13, 14]三种方法。面元法和等效盘模型具有方法简单、计算网格量小和计算速度快等特点。等效盘模型方法假设螺旋桨前方气流只有轴向速度,而未考虑螺旋桨前方气流的旋转效应,不能满足以尾部螺旋桨推进为动力的高空长航时无人机滑流效应研究的要求,应用等效盘模型的方法研究尾部推进螺旋桨飞机的滑流效应对全机的气动影响存在很大的局限性。螺旋桨数值模拟方法可以模拟螺旋桨的前后流动现象,具有计算精度高等特点。在螺旋桨流场数值模拟中,目前主要采用以下三种计算模型:MRF模型、混合平面模型和滑动网格模型[15]。前两种模型均假设流动是定常的,旋 转部件和静止部件之间的效果是近似平均的。滑动网格模型假定流动是非定常的,因此可以更加真实地模拟旋转部件和静止部件之间的相互作用,但是滑动网格模型使用非定常的数值模拟求解方法,在网格质量和计算资源方面的要求比前两种模型苛刻得多。对于相同的计算网格和计算设备,滑动网格模型数值计算消耗时间约为MRF法的7~8倍。在迭代残差方面,滑动网格收敛的残差需为MRF法的1/50~1/100。两种方法计算结果偏差较小,考虑到节省计算的时间和资源,一般使用MRF模型[15]。
本文采用MRF模型模拟螺旋桨的旋转,同时兼顾螺旋桨的轴向和旋转效应,应用数值模拟方法开展对推进式螺旋桨高空长航时无人机的滑流效应影响研究。
1 MRF模型 1.1 MRF模型MRF模型是一种常用而简便有效的流体旋转运动定常计算方法,广泛运用于旋转流体机械领域和螺旋桨设计领域。MRF模型的基本思想是把计算网格区域分为旋转区域和固定区域。将螺旋桨所在的旋转区域内的流场简化为桨叶在某一位置的瞬时流场,将非定常问题用定常方法计算。旋转区域的网格在计算时保持静止,在旋转系坐标系中以作用的科氏力和 向心力进行定常计算;而飞机所在的固定区域则按照惯性系坐标进行定常计算。在两个子区域的交界处交换惯性坐标系下的流体参数,保证了交界面的连续性,达到了用定常计算来研究非定 常问题的目的[15]。
控制方程采用旋转坐标系下的雷诺平均Navier-Stokes(N-S)方程,定义如下:
其中,Ω为控体体积,S为控体表面。 U 是守恒量矢量,FI 为无粘通量,Fv 为粘性通量,ST为源项,定义如下:
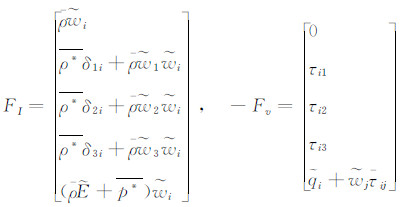
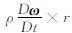 在定常计算中被忽略,因此MRF法不能精确表达运动随时间变化的数值,得到定常解可以看成是非定常解对时间的平均值。所以,MRF又被形象地称为流动的“snapshot”(快照)解[16]。
1.2 算例验证
在定常计算中被忽略,因此MRF法不能精确表达运动随时间变化的数值,得到定常解可以看成是非定常解对时间的平均值。所以,MRF又被形象地称为流动的“snapshot”(快照)解[16]。
1.2 算例验证
采用MRF方法对某双叶螺旋桨进行数值模拟研究,外形如图 2(a)所示。螺旋桨飞行高度H=0 km、来流速度Vo=8 m/s,特征剖面上的雷诺数Re=(0.3~0.5)×106,网格单元数约为150万。计算结果与实验结果对比如图 3所示。从图中可以得出,MRF计算获得的推力和扭矩结果与地面实验结果对比吻合较好,平均误差在8%左右。
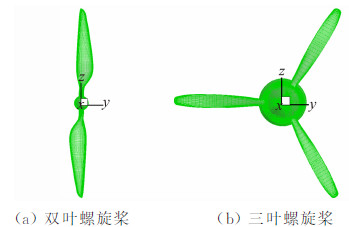 |
| 图 2 螺旋桨外形表面网格示意图Fig. 2 The wall grid on propeller |
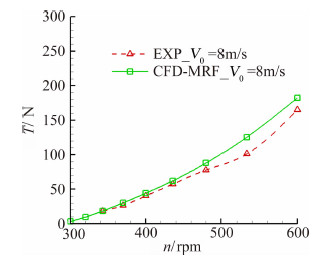 |
| 图 3 螺旋桨推力MRF计算结果和实验测试结果比较Fig. 3 Comparison of propeller thrust results between MRF and experiment of deferent rotate speed |
采用MRF方法对本文研究选用的三叶螺旋桨进行数值模拟研究,外形如图 2(b)所示。飞行高度H=0 km、来流速度Vo=45 m/s,螺旋桨特征面的雷诺数Re=(2.0~3.0)×106,网格单元数约为200万。应用MRF计算和片条理论工程方法计算不同转速的推力,如图 4所示。结果表明MRF计算螺旋桨的推力与工程算法结果相近,计算结果比工程估算略大,平均误差在5%左右。 以上两个验证算例表明本文应用的MRF模型计算结果合理可信,可以模拟螺旋桨的真实气动效应。
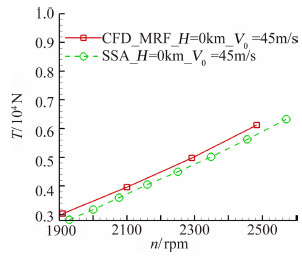 |
| 图 4 螺旋桨MRF和片条理论计算推力结果比较Fig. 4 Comparison of propeller thrust computational results between MRF and SSA(Standard Strip Analysis) of deferent rotate speed |
本文研究的推进式螺旋桨无人机布局如图 5所示,应用MRF模型计算获得全机起飞、爬升和巡航各飞行状态有无螺旋桨旋转下,滑流效应对全机的气动特性影响。气动系数计算以机头顶点为原点(0,0,0),力矩参考点为无人机的重心位置(7.50 m,0,0),俯仰力矩系数以低头为正,抬头为负。计算气动力系数以机翼面积作为参考面积Sref=32 m2,机翼的平均气动弦长为参考弦长Cref=1.76 m。各飞行状态计算条件见表 1所示。
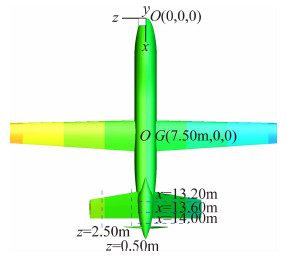 |
| 图 5 计算坐标和V尾截面位置定义Fig. 5 Calculation coordinate and V-tail section defined |
| 飞行状态 | 迎角α /(°) | 高度H /km | 推力T /N | 来流速度V 0/ (m·s -1) | 转速n /rpm |
| 起飞 | 4 | 0 | 6 020 | 45 | 2 500 |
| 爬升 | 4 | 3 | 3 365 | 55 | 2 400 |
| 巡航 | 2 | 7 | 1 150 | 75 | 2 290 |
有无螺旋桨两个模型计算网格单元分别为620万和560万。全机有无螺旋桨滑流效应影响空间流线对比,如图 6所示,可以看出滑流对流线进行收缩加速和旋转。V尾表面压力分布图对比,如图 7所示。从图 7中可以看出无螺旋桨时左右V尾的压力分布是对称的,有螺旋桨则压力分布不对称。全机有无螺旋桨滑流效应影响计算数据见表 2所示。
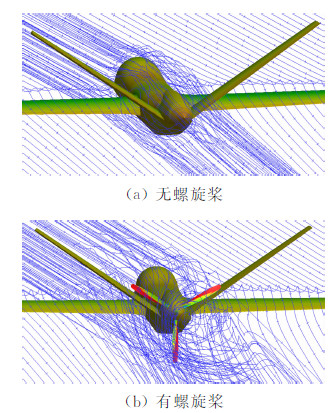 |
| 图 6 有无螺旋桨模型全机空间流线对比Fig. 6 Comparison of stream trace of the UAV model with and without propeller |
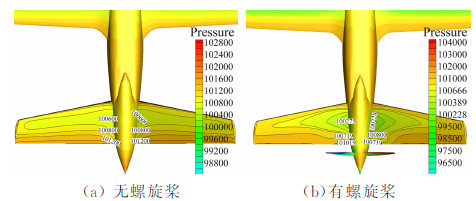 |
| 图 7 起飞状态全机有无螺旋桨V尾压力分布图对比Fig. 7 Comparison of pressure on V-tail with and without propeller slipstream effects at taking off status, attack angle α=4° |
| 各飞行状态 | α /(°) | C l | C d | C z | C mx | C my | C mz | C l/C d | |
| 起飞 | 4 | 1.0012 | 0.0390 | 0.0001 | 0.0002 | -0.0004 | 0.0007 | 25.70 | |
| 全机无桨 | 爬升 | 4 | 1.0024 | 0.0393 | 0.0002 | 0.0002 | -0.0005 | 0.0005 | 25.51 |
| 巡航 | 2 | 0.8045 | 0.0312 | 0.0001 | 0.0002 | -0.0004 | -0.0283 | 25.76 | |
| 起飞 | 4 | 1.0135 | 0.0495 | -0.0020 | -0.0018 | 0.0053 | 0.0379 | 20.48 | |
| 全机带桨 | 爬升 | 4 | 1.0084 | 0.0445 | -0.0012 | -0.0001 | 0.0035 | 0.0209 | 22.67 |
| 巡航 | 2 | 0.8039 | 0.0323 | -0.0006 | 0.0001 | 0.0016 | -0.0308 | 24.88 |
从表 2中的计算结果可以得出,起飞时由于螺旋桨处于大功率工作状态,滑流效应对全机的气动特性影响非常明显,相比无桨模型升力系数Cl增加0.0123,阻力系数Cd增加0.0105,升阻比下降5.2个点,滚转力矩系数Cmx增加-0.002,偏航力矩系数Cmy增加0.0057,俯仰力矩系数Cmz增加0.0372。从图 8机翼截面z=±0.80 m压力分布以及图 9全机流线对比,可以看出起飞状态,机翼已经不受到滑流的加速效应的影响,因此推断爬升和巡航状态机翼都不受到滑流效应的影响。全机起飞状态阻力系数急剧增加,主要原因还是由于桨盘载荷过大和螺旋桨转速过高,使得V尾和机身尾段压差阻力急剧增大造成的。起飞状态由于螺旋桨滑流效应影响,无人机的气动性能急剧下降,严重影响无人机的爬升性能,因此对于尾部螺旋桨推进的高空长航时无人机的机身尾段气动外形设计必须要考虑螺旋桨滑流的影响,进行减阻优化设计,提高无人机的爬升性能。
 |
| 图 8 起飞状态α=4°,z=±0.80 m机翼截面压强分布对比Fig. 8 Comparison of pressure coefficient along section z=±0.80 m of wing with and without propeller slipstream effects at taking off status, attack angle α=4° |
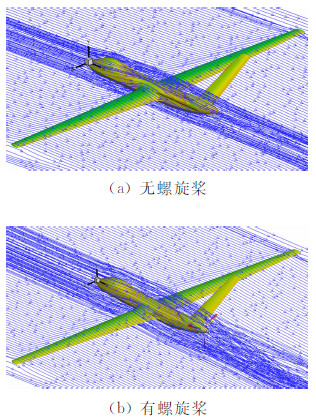 |
| 图 9 有无螺旋桨模型机翼空间流线对比Fig. 9 Comparison of stream trace of the UAV wing with and without propeller |
爬升状态,螺旋桨功率减小,滑流效应影响相对减弱。相比无桨状态,升力系数Cl增加0.006,阻力系数Cd增加0.0052,升阻比下降2.8个点,滚转力矩系数Cmx增加-0.0003,偏航力矩系数Cmy增加 0.004,俯仰力矩系数Cmz增加0.0204。
巡航状态,螺旋桨功率最小。相比无桨状态,升力系数Cl增加-0.0006,阻力系数Cd增加0.0011,升阻比下降0.9个点,俯仰力矩系数Cmz增加-0.0025。此时螺旋桨滑流效应对全机的气动特性影响已经很微弱。
2.2 加速效应和旋转效应影响分析推进式螺旋桨布局无人机的加速效应在全机上表现为气动力增加,如升力和低头俯仰力矩的增加。部件上则是压力分布的变化,如V尾截面压力分布的面积增大;旋转效应在全机上的表现为全机Cmx变化,部件上则是V尾截面压力分布出现偏转。
图 10~图 12为起飞状态V尾截面压强分布图。如图 10所示,受滑流旋转效应影响z=0.50 m位置截面后缘压强相对于z=-0.50 m位置截面后缘压强往上翘,表现为螺旋桨的旋转效应对V尾后缘处当 地迎角产生变化的影响,受到加速效应影响V尾截面上压强分布面积明显比无滑流状态时要大;如图 11所示在V尾截面z=±1.5 m位置,V尾截面上的压强分布不对称性基本消失,可以得出螺旋桨滑流旋转效应对V尾的影响范围为桨径1.2倍(螺旋桨半径R =1.25 m);滑流加速效应对V尾截面上压强分布的影响由内到外逐步减弱,如图 12所示,到z=±2.50 m 截面处,V尾截面上环量已经不受滑流效应影响,滑流对V尾的加速效应影响区域直径约为螺旋桨直径的2倍。
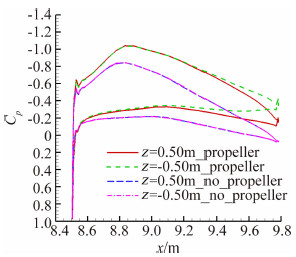 |
| 图 10 起飞状态α=4°,z=±0.50 m截面压强分布对比Fig. 10 Comparison of pressure coefficient along section z=±0.50 m with and without propeller slipstream effects at taking off status, attack angle α=4° |
 |
| 图 11 起飞状态α=4°,z=±1.50 m截面压强分布对比Fig. 11 Comparison of pressure coefficient along section z=±1.50 m with and without propeller slipstream effects at taking off status, attack angle α=4° |
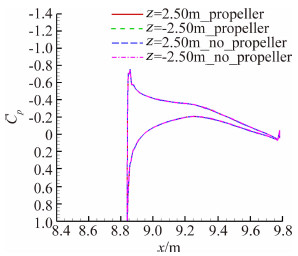 |
| 图 12 起飞状态α=4°,z=±2.50 m截面压强分布对比Fig. 12 Comparison of pressure coefficient along section z=±2.50 m with and without propeller slipstream effects at taking off status, attack angle α=4° |
爬升状态前进速度V0增大以后,通过分析V尾各截面上的压强分布得到旋转效应区域为桨径直径约0.8倍。滑流加速效应影响区域为桨径1.6倍。滑流效应对V尾的影响明显减弱。巡航状态前进速度V0进一步增大,通过分析V尾各截面上的压强分布得到旋转效应和加速效应对V尾的影响已经很微弱。
螺旋桨滑流对左右侧V尾的影响,如图 13所示。从图中可以得出在起飞状态左右气动力出现极大不对称,整副V尾的Cmx绝对值最大,左右侧V尾的Cmz的偏差和相对无桨的增量也同时达到最大值;爬升状态V尾的Cmx减小和左右侧尾翼的Cmz偏差减小;巡航状态V尾的Cmx最小,同时左右侧Cmz偏差达到最小。从图 14得出滑流效应对机翼的滚转力矩和俯仰力矩基本上不影响。
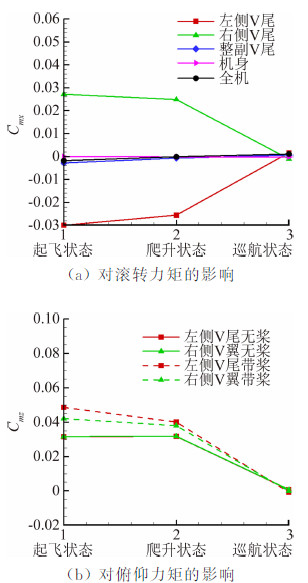 |
| 图 13 有无螺旋桨对V尾滚转力矩和俯仰力矩的影响Fig. 13 Comparison of Cmx and Cmz of the UAV V-tail with and without propeller |
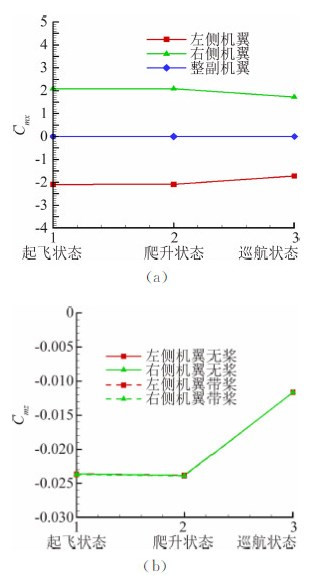 |
| 图 14 有无螺旋桨对机翼滚转力矩和俯仰力矩的影响Fig. 14 Comparison of Cmx and Cmz of the UAV wing with and without propeller |
本节针对起飞状态无人机受滑流效应影响气动特性急剧下降等问题开展进一步研究,分析了起飞状态H=0 km,α=4°和V0=45 m/s的不同推力和相同推力不同桨距两种情况下滑流效应对无人机气动特性的影响,研究状态如表 3所示。研究结果表明全机的升力系数增量随推力变化影响较小,阻力系数变化较大,导致全机升阻比随着推力增加下降很大,如图 15所示。因此对于尾部螺旋桨推进的飞机在进行起飞-爬升状态桨发匹配设计时,要充分考虑滑流对全机气动性能的影响,兼顾动力匹配和滑流对爬升性能影响。设计目标即要满足飞机动力要求,同时还必须保证飞机具有足够的爬升性能。
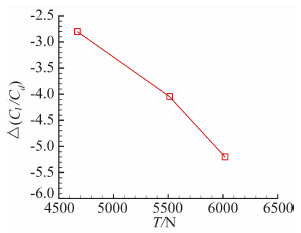 |
| 图 15 不同推力状态下滑流效应对全机升阻比增量影响Fig. 15 The increment of lift-to-drag of UAV in different thrust of propeller status |
| 螺旋桨状态 | 转速n /rpm | 推力T /N | 桨距θ /(°)(r/R =0.75径向截面安装角) |
| 1 | 2 100 | 4 670 | 25.08 |
| 2 | 2 300 | 5 513 | 25.08 |
| 3 | 2 500 | 6 020 | 25.08 |
| 4 | 2 100 | 6 055 | 31.08 |
不同桨距相同推力下得到螺旋桨滑流效应影响全机的气动力系数增量基本相同,如图 16所示为不同桨距螺旋桨滑流效应影响全机的升阻比增量对比,这表明在相同推力下滑流效应影响基本相同与转速无关。
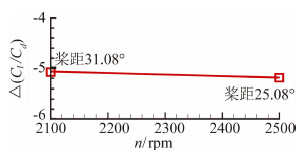 |
| 图 16 不同桨距螺旋桨滑流效应对全机升阻比增量影响Fig. 16 The increment of lift-to-drag of UAV in different blade attack angle status |
本节最后分析了起飞状态下滑流效应对全机升阻特性的影响。如表 4所示为滑流效应对全机各部件的升阻力系数增量影响数据结果。从表 5可以得出全机升力系数增加0.0123,相对于无滑流效应状态全机升力系数增加1.2%;阻力系数受到滑流效应影响变化较大,全机阻力系数增加0.0105,主要是压差阻力增大造成的,粘性阻力增加很小,相对无滑流效应状态全机阻力增加26.6%;其中V尾增加5.3%、机翼增加1.0%和机身增加20.3%;阻力系数增加主要来自机身,由于滑流效应对机翼的影响非常小,因此阻力系数增量主要是来源于螺旋桨附近的机身后段。
| 名称 | ΔC l | ΔC l/C l | ΔC d | ΔC d_V | ΔC d_p | ΔC d/C d |
| 全机 | 0.0123 | 1.2% | 0.0105 | 0.0003 | 0.0102 | 26.6% |
| V尾 | 0.0033 | 0.3% | 0.0021 | 0.0002 | 0.0019 | 5.3% |
| 机翼 | 0.0069 | 0.7% | 0.0004 | 0.0000 | 0.0004 | 1.0% |
| 机身 | 0.0021 | 0.2% | 0.0080 | 0.0001 | 0.0079 | 20.3% |
本节从机身后段的各截面(截面定义如图 5所示)压强分布变化情况,分析阻力系数急剧增加的主要原因。如图 17~图 19所示为机身尾部有无螺旋桨的压强系数分布对比。机体截面的压强受到滑流效应影响以后,压强分布往低压方向平移量很大,而且截面上下物面压差进一步增大,同时压强分布也出现剧烈的不对称性,表明机身尾段受到加速效应和旋转效应影响都非常明显,这正是造成机身尾段压差阻力增加的主要原因。
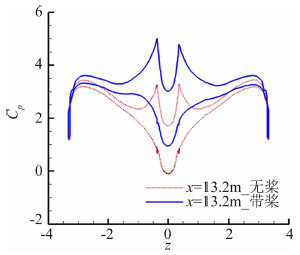 |
| 图 17 x=13.2 m截面机身+V尾表面压强系数分布对比Fig. 17 Comparison of coefficient pressure distribution in x=13.2 m section of UAV with and without propeller |
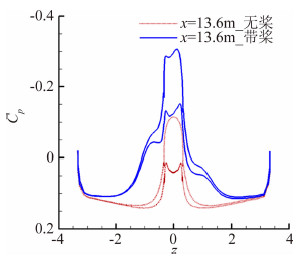 |
| 图 18 x=13.6 m截面机身+V尾表面压强系数分布对比Fig. 18 Comparison of coefficient pressure distribution in x=13.6 m section of UAV with and without propeller |
 |
| 图 19 x=14.0 m截面机身表面压强系数分布对比Fig. 19 Comparison of coefficient pressure distribution in x=14.0 m section of UAV with and without propeller |
起飞状态时螺旋桨推力最大,螺旋桨对桨盘前方的气流加功量达到最大。桨盘前方气流流管急剧收缩加速和旋转,使得V尾所在流场受到很强的加速和旋转效应影响,所以此时V尾受到加速效应和旋转效应的影响范围,以及全机气动力系数的影响增量均达到最大。爬升状态时螺旋桨推力减小,桨盘前方气流加速和旋转特性影响减弱,因此滑流效应对V尾的影响范围减小,全机气动力系数增量影响也同时减弱。巡航状态时螺旋桨推力最小,桨盘前方气流加速和旋转特性影响最弱,所以此时滑流对V尾的影响范围是最小的,全机气动力系数基本不受影响。
总体来看,螺旋桨滑流效应影响强度随推力增加而增大,随来流速度增大而减小,由无人机纵向对称面向外逐渐减弱。无人机起飞升阻比随着推力增大而急剧下降,相同推力不同桨距得到滑流效应影响结果基本相同。起飞状态飞机受滑流效应影响机身尾部压差阻力急剧增加,导致全机气动特性下降。滑流效应只能够影响到无人机后段机身和V尾部分的气动特性,对于机翼部分则基本上影响不到。加速效应使得全机的气动力系数增大,造成俯仰力矩增加。旋转效应使得V尾表面压力出现不对称,造成全机滚转力矩和偏航力矩增加。在滑流效应影响下无人机的纵向、横向和航向力矩均需要重新配平。
3 总结本文应用MRF模型的数值模拟方法开展对高空长航时无人机螺旋桨滑流效应影响研究。计算获得螺旋桨滑流效应对V尾和全机气动力系数的影响结果,分析了螺旋桨滑流效应对无人机的起飞、爬升和巡航气动特性的影响。通过对V尾+单桨组合和全机的滑流效应影响研究得出以下结论:
(1) 采用MRF模型的数值模拟方法能够较好地模拟螺旋桨滑流加速效应和旋转效应对气动特性的影响。该方法具有重要的工程应用价值,可以为螺旋桨飞机气动设计提供技术支持。
(2) 起飞状态螺旋桨滑流效应对全机气动特性影响最强,气动力系数增量最大。爬升状态螺旋桨滑流效应影响减弱。巡航状态螺旋桨滑流效应的影响最小,气动特性基本不变。起飞状态飞机受滑流影响机身尾部压差阻力急剧增加,导致全机气动性能下降。
(3) 螺旋桨滑流效应影响强度随推力增加而增大,随来流速度增大而减小,由无人机对称面向外逐渐减弱,相同推力条件下滑流效应的影响基本相同。滑流效应只能够影响到机身后段和V尾部分的气动特性,对于机翼部分则基本上影响不到。对于机身尾段设计需要考虑滑流影响进行优化设计。桨发匹配时需要兼顾动力设计和滑流效应对全机气动性能的影响。
(4) 加速效应使得全机气动力系数增大,造成俯仰力矩增加。旋转效应使得V尾表面压力出现不对称,造成全机滚转力矩和偏航力矩增加。
| [1] | J. Aurg MAuller, Marianne Aschwandeny. Wind tunnel simulation of propeller effects in the A400M FLA-4 Model[R]. AIAA 2005-3706. |
| [2] | Li Zhengchu, Wang Xunnian, Chen Hong, et al. Experimental study on the influence of propeller slipstream on wing flow field[J]. Journal of Experiments in Fluid Mechanics, 2000, 14(2):44-48. (in Chinese) 李征初, 王勋年, 陈洪, 等. 螺旋桨滑流对飞机机翼流场影响试验研究[J]. 流体力学实验与测量, 2000, 14(2):44-48. |
| [3] | Jiang Xiaoli, Yang Shipu. Analysis of propeller aircraft slip stream mechanism[J]. Journal of Design and Research in Civil Aviation Aircraft, 2009, (4): 34-38. (in Chinese) 蒋晓莉, 杨士普. 螺旋桨飞机滑流机理分析[J]. 民航飞机设计与研究, 2009, (4): 34-38. |
| [4] | Gilles Fratello, Daniel Favier, Christian Maresca. Experimental and numerical study of the propeller/fixed wing interaction[J]. Journal of Aircraft, 1991, 28(6): 5-9. |
| [5] | Qin E, Yang Guowei, Li Fenglan, et al. Analysis of propeller slipstream on numerical aerodynamic effects[J]. Journal of Northwestern Polytechnical University, 1997, 15(4): 511-516. (in Chiense) 鄂秦, 杨国伟, 李凤蔚, 等. 螺旋桨滑流对飞机气动特性影响的数值分析[J]. 西北工业大学学报, 1997, 15(4): 511-516. |
| [6] | Conway J T. Analytical solutions for the actuator disk with variable radial distribution of load[J]. Fluid Mech., 1995, 297: 327-355. |
| [7] | Chaffin M S.A guide to the use of the pressure disk rotor model as implemented in INS3D-UP[R].NASA CR4692, 1995. |
| [8] | Veldhuis L L M, Nebiolo S. Analysis of calculated and measured wake characteristics of a propeller-wing model[R]. AIAA 2000-0908. |
| [9] | Zuo Suihan, Yang Yong. Numerical analysis of dynamic characteristics of propeller slipstream influence with the wing trailing edge flap gas[J]. Aeronautical Computing Technique, 2007, 37(1): 54-57.(in Chinese) 左岁寒, 杨永. 螺旋桨滑流对带后缘襟翼机翼气动特性影响的数值分析[J]. 航空计算技术, 2007, 37(1): 54-57. |
| [10] | Li Bo, Liang Dewang, Huang Guoping. The slipstream impact on turboprop aircraft aerodynamic performance based on the equivalent plate model[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(4): 845-852. (in Chiense) 李博, 梁德旺, 黄国平. 基于等效盘模型的滑流对涡桨飞机气动性能的影响[J]. 航空学报, 2008, 29(4): 845-852. |
| [11] | Moens F, Gardarein P. Numerical simulation of the propellering/wing interactions for transport aircraft[R]. AIAA 2001-2404. |
| [12] | Hall E Jo, Top D A, Delaney R A. Task 7- ADPAC users manual. cleveland: NASA Lewis Research Center[R]. NASA CR-195472. |
| [13] | Xu Heyong, Ye Zhengyin. The unsteady flow numerical simulation of propeller slipstream[J]. Journal of Aerospace Power, 2011, 26(1): 148-153.(in Chinese) 徐和勇, 叶正寅. 螺旋桨非定常滑流数值模拟[J]. 航空动力学报, 2011, 26(1):148-153. |
| [14] | He Wei. Comparison of multiple reference frame method and sliding mesh method in numerical simulation of automobile front air intaking[J]. Computer Aided Engineering, 2007, (3): 96-100.(in Chinese) 何炜. 多参考坐标系法和滑移网格法在汽车前端进气数值模拟中的比较[J]. 计算机辅助工程, 2007, (3): 96-100. |
| [15] | liu Peiqing. Air propeller theory and its application[M]. Beijing: Beihang University Press, 2006, 2.(in Chinese) 刘沛清. 空气螺旋桨理论及其应用[M]. 北京: 北京航空航天大学出版社, 2006, 2. |
| [16] | Deglon D A, Meyer C J. CFD modeling of stirred tanks numerical considerations[J]. Minerals Eng., 2006, 19(10): 1059-1068. |