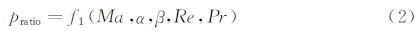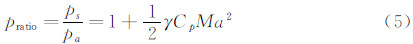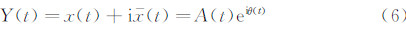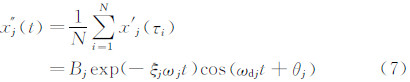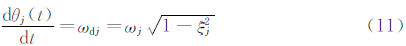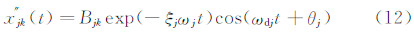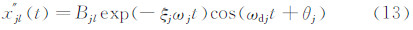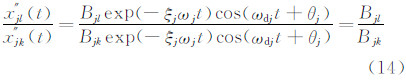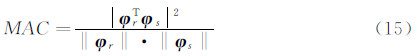0 引言

大跨度屋盖结构等自振频率较低的结构体系在发生振动时，会带动周边的空气一起运动，从而产生附加质量和气动阻尼，这是该类结构体系风振分析中必须考虑的重要影响因素。在静止空气环境等理想条件下，附加质量和气动阻尼可采用势流理论进行分析^{[1, 2, 3, 4]}，其可行性已由实验得以证实^[5]，但在脉动风作用下，附加质量和气动阻尼会发生变化，此时需通过实验研究其变化规律。

由于附加质量的变化主要体现在其对结构自振频率的影响，而气动阻尼可使总阻尼发生变化，所以该类问题的研究可归结于模态参数识别^{[6, 7]}。武岳等^[8]对两种不同矢跨比的鞍形索膜结构进行了气弹模型风洞实验，采用截频滤波及随机减量方法提取了不同风速及风向角下的附加质量和气动阻尼。卢旦等^[9]联合采用经验模态分解、Hilbert变换及随机减量法从平屋盖气弹模型的动力响应数据提取了气动阻尼，并研究了迎风面开孔对气动阻尼的影响。曹会兰等^[10]则采用四参量随机特征表达式对方形截面超高层建筑的横风向气动阻尼进行了分析。以上研究均集中在对频率和阻尼比的提取，但由于在脉动风作用下结构响应是一个宽频带过程且受迫振动特征明显，对于柔性的大跨度屋盖结构而言还会受应力刚化的影响，故在将模态参数识别应用于附加质量和气动阻尼的研究时，还应考虑各模态阶次初始参量与识别参量之间的振型相似关系。

HHT是由Huang等^[11]于1998年提出的一种时间序列信号处理方法，由经验模式分解(Empirical Mode Decomposition，EMD)及Hilbert变换(Hilbert Transform)两部分组成。

EMD对信号进行平稳化处理，将信号中不同尺度的波动分解开来，产生一系列具有不同特征尺度的数据序列，每一个序列称为一个本征模函数分量(Intrinsic Mode Function,IMF)。

EMD的具体做法是：找出原数据序列x(t)所有的极大值及极小值点并用三次样条函数拟合成上下包络线，用x(t)减去上下包络线的平均值可得一新的数据序列h₁(t)，重复此过程直至前后两次新数据序列的标准差:

点击浏览公式

点击浏览公式

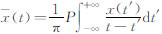对给定的时间序列x(t)进行Hilbert变换可得数据序列，其中P为Cauchy主值。则幅值A(t)、相位角θ(t)及瞬时频率ω(t)分别为:

点击浏览公式

点击浏览公式

点击浏览公式

而x(t)的解析信号Y(t)可以表示为：

点击浏览公式

设x(t)是风荷载激励下的结构响应时间序列信号，则可对x(t)作IIR带通滤波后进行经验模态分解，在带通滤波时相比FIR滤波器，IIR滤波器能更有效地滤除低频影响从而得到所需的频带信号。其中带通区间可根据傅里叶谱初步估计得到，本文以峰值频率为中心取对称区间，半带宽范围取与相邻谷值频率之差及半功率点中的较小值。若要得到第j阶模态响应，则将每一个时间序列信号通过带通滤波频率为ω_jL<ω_j<ω_jH的滤波器，可得时间序列信号x_j(t)，对其进行经验模态分解，则得到的第一阶IMF，记为x′ _j(t)，一般就非常接近结构的第j阶模态响应。

经验模态分解得到的x′ _j(t)为平稳随机信号，可由随机减量法^{[12, 13]}得对应的自由衰减响应。设x′ _j(t)触发值为x₀的时刻分别为t₁,t₂,…,t_N，以这些时刻为起点对x′ _j(t)截取子信号段x′ _j(τ_i)(i=1,…,N)，其中τ_i=t－t_i(t_i=t₁,…,t_N)。将各子信号段进行集合平均即得自由衰减信号：

点击浏览公式

对x_j^″(t)进行Hilbert变换并构建相应的解析信号Y_j(t)=A_j(t)e^iθ_j(t)，则幅值和相位角可分别表示为：

点击浏览公式

点击浏览公式

点击浏览公式

联合求解式(10)及(11)即可得第j阶模态的频率和阻尼比。实际求解时可由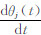的平稳部分取平均值得ω_dj，再对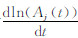进行线性拟合，由其斜率求解ξ_j。

假设结构有n个自由度，并在随机减量法中以第k个自由度的触发值时刻点为参考，对其它自由度方向对应第j模态的IMF信号同步截取子信号段并作集合平均，则可以得到结构以第j模态坐标所作的自由振动衰减信号。其中，第k和l自由度方向的衰减信号可分别表示为：

点击浏览公式

点击浏览公式

由(12)和(13)即可得：

点击浏览公式

由于B_jk及B_jl仅与第k及l自由度方向的模态坐标有关，故由上式可知模态振型可用各自由度方向与参考方向的自由衰减信号之比表示。

模态振型 φ _r和 φ _s之间的相似关系可用模态置信判据(Modal Assurance Creterion，MAC)^{[6, 7]}来表示：

点击浏览公式

若MAC≈1，则表明 φ _r和 φ _s本质上为同一模态。设同一模态下静止空气中结构的频率为ω_sj，而脉动风作用下的识别频率为ω_dj，则附加质量的改变量可表示为：

点击浏览公式

第j阶模态的气动阻尼改变量则可以表示为：

点击浏览公式

图 1所示为一两自由度系统，m₁=m₂=1 kg，c₁=c₂=2.0 N·s/m，k₁=k₂=1000 N/m。在质量块m₁和m₂上分别施加互不相关的白噪声激励力，采用Runge-Kutta法进行求解，并以100 Hz的采样频率得到结构的位移响应，共采样20 s。

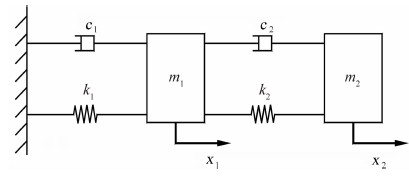图 1 两自由度系统Fig. 1 The system of two degree of freedom

图选项

图 2为m₁和m₂的位移响应及其谱密度(图中x₁、x₂分别为m₁、m₂的自由度坐标，如图 1所示)，为模拟实际情形，对输出信号施加了10%的噪声。由此可见，白噪声所激发的相应于第二频率分量的能量远低于第一频率分量。若直接对原始信号进行EMD分解，并不能得到第二频率分量信号，但在IIR带通滤波后再作EMD分解则可以很好地提取出两阶IMF信号。图 3所示为两阶IMF的随机减量信号，据此可得频率、阻尼比及振型的识别结果如表 1所示。由此可见，本文方法对各阶模态参数的识别精度是非常理想的，可以被很好地应用于脉动风作用下的附加质量及气动阻尼识别。

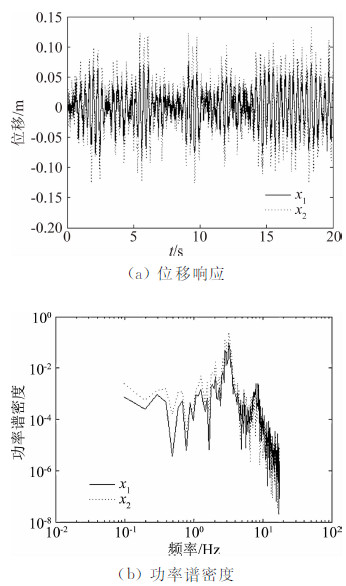图 2 位移响应及其功率谱密度Fig. 2 The displacement signals and their power spectrum density

图选项

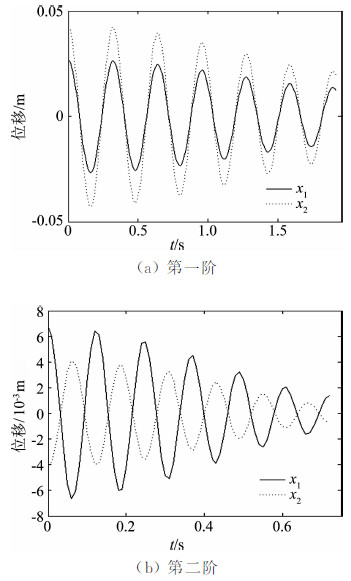图 3 随机减量信号Fig. 3 The random decrement signals

图选项

图 4为一肋环型索穹顶模型的风洞实验图，模型顶部覆盖塑料膜以传递风荷载，模型跨度1 m，矢跨比1/5，谷索与水平线夹角均为15°，中心压杆预应力水平为1 N。静止空气环境中测得模型的第一阶反对称模态频率为7.29Hz，阻尼比2.76%。在模型中1、 2两点分别布置三向加速度传感器，采样频率500 Hz，B类地貌，风速3 m/s、5 m/s、8 m/s及10 m/s，来流风速及湍流度剖面如图 4(c)所示。

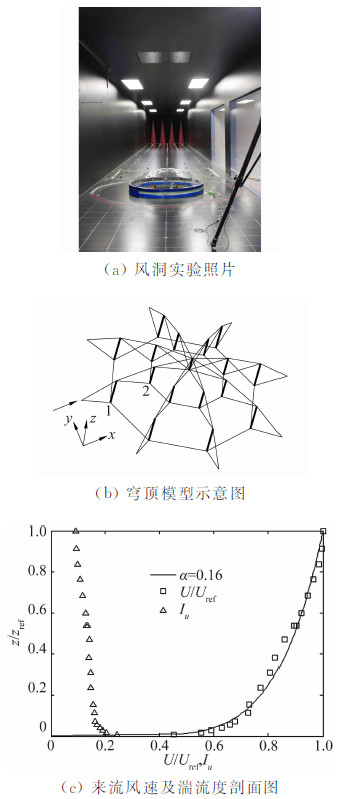图 4 肋环型索穹顶风洞实验Fig. 4 Wind tunnel test for the Geiger type cable system

图选项

图 5所示为测点2在y自由度方向采用welch法^[14]计算的功率谱密度分布，welch法采用加Hanning窗交叠求功率谱，可以有效减小方差及偏差，其主瓣包含更多能量因而使功率谱的主瓣较窄，分辨率较高。由图 5可以看出覆盖膜在风速较低时(3 m/s)的低频振动较为明显。对图中所标峰值频率按前述方法识别模态振型，并与静止空气环境下的第一阶振型试验结果进行比较，可求得MAC值如表 2所示(对于肋环型索穹顶结构的第一阶反对称模态，测点1、2的六个自由度方向即可表示其振型)，故由表 2可以看出图 5所标峰值频率确实对应第一阶反对称模态。

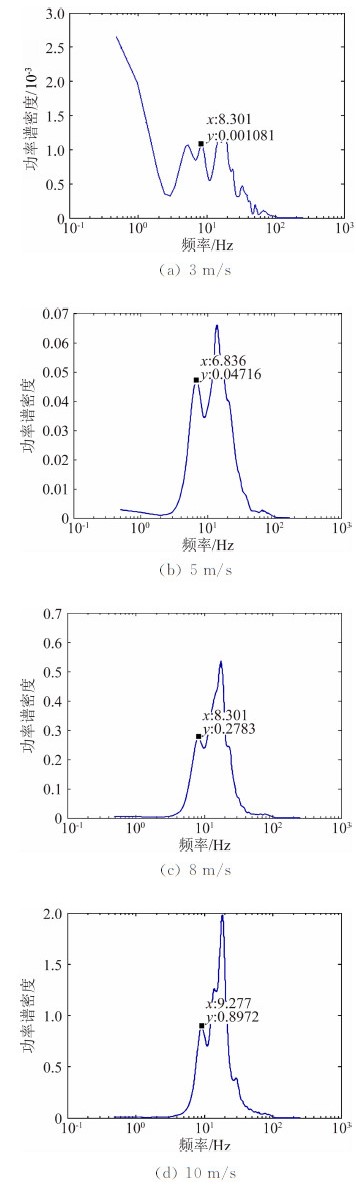图 5 测点2在y自由度方向的功率谱密度Fig. 5 The power spectrum density of point 2 along y degree of freedom

图选项

依据振型相似的要求，即可由频率、阻尼识别结果和式(16)、(17)求得脉动风作用下第一阶反对称模态的附加质量及气动阻尼改变量如表 3所示(实验中对外圈环索的测力结果表明，在风速10 m/s时其时均预张力的变化不超过6%，由于索穹顶结构的刚度由预张力提供，因此刚度变化对频率的影响可忽略不计)。由此可见，与静止空气环境相比，在风速较低时附加质量和气动阻尼都随着风速的增加而上升，并在某一风速下达最大值，随后下降，这与文献^[15]的理论推导结果比较一致，而气动阻尼随风速的变化规律则与文献^{[16, 17]}相吻合。由于测点有限，本文未对高阶模态附加质量及气动阻尼变化规律进行研究。

对于自振频率较低的大跨度屋盖等结构体系而言，其在脉动风作用下附加质量和气动阻尼的影响不可忽略。静止空气环境下附加质量和气动阻尼的势流理论分析及实验识别研究相对较为简单成熟，而脉动风作用下参数的精确识别则较为困难。此外，截至目前脉动风下附加质量及气动阻尼的识别研究皆未考虑模态振型相似的要求，故本文基于Hilbert-Huang变换及随机减量技术，将随机减量信号应用于模态振型识别，并依据振型相似的原则识别附加质量和气动阻尼，数值算例及实验研究结果表明：

(1) 将原始信号经IIR带通滤波后再作EMD分解可有效抑制噪声的影响，准确提取所需模态阶次的响应信号。其后对所提取的信号应用随机减量技术，并以参考自由度的触发位置为基准时刻点，对各自由度方向同步求解自由衰减信号，则可准确提取所需模态阶次的频率、阻尼比，同时还可获得该阶模态的振型。在此基础上即可依据模态相似原则识别附加质量和气动阻尼(或其改变幅度)。

(2) 肋环型索穹顶的实验识别结果表明，风速较低时附加质量较静止空气环境有所下降，随着风速的增加附加质量也随之提高并在某一风速时达最大值，之后则随风速的增加而下降；气动阻尼则随风速的增加而上升，并在某一风速达最大值后逐渐降低。