0 引 言
亚声速飞行器往往需要加装凸出外形的非升力部件,例如不可收放式起落架的支柱、双翼机上下翼面的支杆、刀形天线、预警机支架等。这些部件一般不要求产生升力或操稳力矩,同时具有明显的二维特性,其气动整流对于飞机气动减阻、结构减重、避免气流分离等具有重要意义,当剖面距离重心较远时还可能对飞机稳定性带来负面影响,对于改型设计飞机而言通常需要降低其剖面升力效率从而减小对气动稳定性的影响。
椭圆剖面由于具有二阶光顺、保凸性好、构造简单等优点,是飞机外形常用的剖面外形。Hoerner指出当附面层处于湍流状态时椭圆剖面在长细比5-9时具有的最小阻力,其升力线斜率小于常规翼型且与雷诺数关系密切[1, 2]。近年来椭圆剖面作为一种前后对称翼型在倾转机翼飞机/无人机中得到了较多关注和研究,Kwon、詹浩,邓阳平等采用风洞实验方法对不同雷诺数下16%厚度的椭圆翼型的气动及流场特性进行了研究[3, 4, 5, 6]。Kwon、Chitta 、Benazza、Assel等对椭圆剖面气动特性开展了数值计算研究[7, 8, 9, 10]。椭圆剖面在超声速导弹弹体、地面雷达罩外形等领域也有研究及应用[11, 12]。包括椭圆在内的翼型在低雷诺数(Re<5×105)时性能由于层流气泡的存在而恶化,目前还缺少能够较准确预测层流气泡和转捩的RANS模型[9],本文研究的椭圆剖面Re数大于2×106,与选用的高Re数RANS湍流模型是匹配的。翼型剖面也是气动整流常用的剖面外形,但此类剖面常用的长细比一般大于3,当长细比进一步减小则会导致较严重的气流分离,甚至出现升力线斜率反号(正迎角增量产生负升力增量)的特殊现象[1]。
上述研究主要以机翼为设计目标,所选取的翼型厚度相对较小,剖面形状一般为标准椭圆,相应的数值计算和风洞试验数据也较为有限。本文以非升力面的整流剖面为研究对象,提出了一种在标准椭圆基础上拓展的变参数椭圆曲线剖面,并综合分析了不同形状和长细比剖面的气动和结构特性,为指导非升力整流剖面外形设计提供参考。
1 变参数椭圆曲线剖面的设计椭圆曲线属于二次曲线的一种,在生成航空气动外形如机身剖面等方面得到了广泛应用。二次曲线的定义见图 1,将平面从不同角度与圆锥相交,当平行于圆锥旋转轴时交线为抛物线,在此基础上平面趋于水平时得到椭圆,而趋于更大倾角时得到双曲线。获得具体的二次曲线坐标点可参考文献[13]给出的图解法。在CAD实际应用中可通过指定两个点、两个切线方向和二次曲线形状参数Rho来构造二次曲线。Rho表征了二次曲线的饱满度,当Rho=0.5时为抛物线,Rho>0.5时为双曲线,Rho<0.5时为椭圆曲线,采用参数Rho控制椭圆的饱满度,相对标准椭圆具有较大的灵活性。
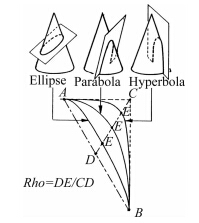 |
| 图 1 二次曲线形状参数Rho的定义 Fig. 1 Definition of conic shape parameter Rho |
本文提出的变参数椭圆曲线剖面具有最大厚度位置可变、二次曲线形状参数可调两个特点,当最大厚度位置选择为50%弦长,Rho选择为0.414时形状为标准椭圆,而最大厚度、Rho选择不同的参数组合就能获得气动、结构特性各异的全新剖面。本文设计的剖面一方面采用了椭圆曲线的生成方法,另一方面借鉴了翼型的外形特征(最大厚度位置靠前,前部饱满而后部尖锐)。
为对比不同剖面的特性,选取标准椭圆、NACA 4位对称翼型以及新设计的两种椭圆曲线剖面进行了对比研究。研究的4类剖面将最大厚度固定为tmax=0.2m,选取c/t=1.5、2、3、4、5、6、8组合为28个剖面外形并进行了数值计算研究,计算风速取为70m/s,基于弦长c的Re=(2~11)×106。上述参数的设定也可理解为对同样的最大厚度tmax求解最优的气动整流剖面。4类剖面的几何特征参数见表 1,外形对比见图 2。
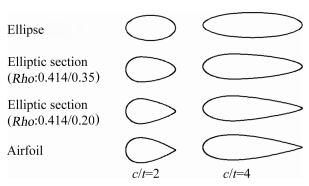 |
| 图 2 剖面外形 Fig. 2 Geometry of sections |
No. | Description | Position of maximum thickness | Forward part Rho | Aft part Rho |
| 1 | Ellipse | 50% cA | 0.414 | 0.414 |
| 2 | Elliptic section Rho=0.414/0.35 | 30% cA | 0.414 | 0.35 |
| 3 | Elliptic section Rho=0.414/0.2 | 30% cA | 0.414 | 0.2 |
| 4 | Airfoil | 30% cA | - | - |
| Note:No.1 is equal to standard ellipse,and No.4 utilizes the thickness distribution of NACA 4 digit symmetric section. | ||||
椭圆剖面的钝后缘存在局部气流分离,因此以雷诺平均N-S(RANS)方程作为数值计算主控方程以研究存在较强粘性力作用的二维剖面气动特性,RANS方程的通用形式为:
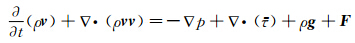
各剖面数值计算均采用了相同的网格拓扑结构和网格设置以保证计算结果的可比性。网格由ANSYS ICEM软件生成,采用了H型的结构化网格,远场边界距离翼型为100tmax,物面设置为无滑移条件,第一层网格高度为10-5 m量级,确保物面的y+值约为1,网格节点数约为30万。
数值求解采用商业软件FLUENT完成,对流项、粘性项均采用二阶迎风格式进行离散,求解器选择为经典的半隐式压力耦合SIMPLE解法,为加速收敛在迭代基本稳定后切换为同时求解速度与压力方程的耦合解法,以数值残差达到或接近10-3,以及气动力停止波动作为计算收敛判据。湍流模型选择二方程的SST k-ω模型,文献[14]指出此模型对于存在气流分离的流场模拟较为准确。
3 计算结果及分析 3.1 算例验证将文献[1、2、5、15]提供的风洞试验数据与数值计算结果进行了对比,结果见图 3。其中NACA0012翼型的计算和试验Re数为9×106,16%厚度椭圆剖面Re数约为2×106。对比可见对NACA0012翼型的升阻特性计算值与试验值吻合较好。16%椭圆剖面的升力特性介于文献[1, 5]试验数据之间,阻力特性与试验值基本相当。椭圆剖面由于对表面流动性质较敏感,且风洞试验数据样本较少,因此难以准确评估计算的可靠度,但CFD研究采用的全湍流附面层假设与本文所研究的剖面Re数所对应的表面流动特性是较为吻合的。
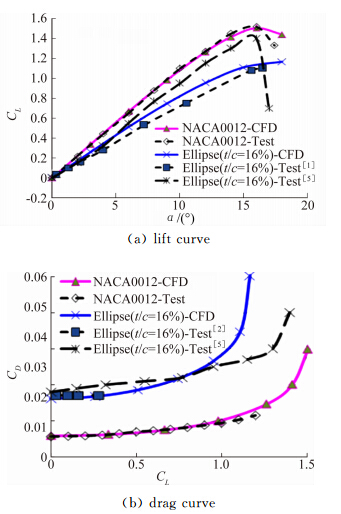 |
| 图 3 CFD结果验证 Fig. 3 Validity study of CFD results |
阻力最小化是气动整流剖面的主要目的之一,4类剖面不同长细比的阻力系数(基于迎风面积)计算结果见图 4。从椭圆剖面 的计算结果来看,阻力系数在c/t>4后处于较低水平,与文献[2]给出的结论吻合,也再次证明了数值计算的可靠度。其它剖面的最小阻力系数在c/t=3~4之间出现最小值,可见为达到阻力最小,剖面应当采用较大的厚度,例如33%。进一步增加厚度至50%对于翼型剖面和给定的两种变参数椭圆剖面阻力增量仍然可接受,剖面尺寸显著缩小,但后续分析表明可能出现负升力 线斜率的问题。
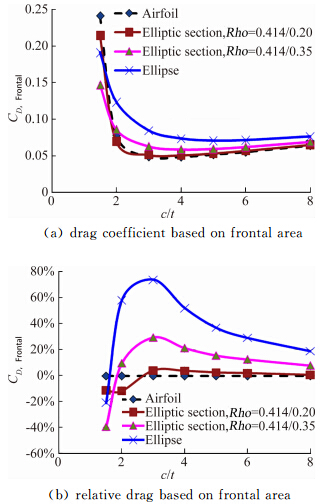 |
| 图 4 剖面阻力特性对比 Fig. 4 Comparison of section drag |
各剖面相对翼型剖面的对比可见,当c/t>3时翼型剖面具有最小的阻力系数,而外形与翼型剖面近似的Rho=0.414/0.2剖面同样具有较低的阻力。当c/t<3时,各椭圆剖面由于后部比翼型饱满,不同程度地减小了尾部分离区大小,阻力得到减小,在此区间内特定的椭圆曲线剖面阻力可能小于翼型剖面,例如c/t=1.5时Rho=0.414/0.35剖面具有最小的尾部分离区,见图 5。
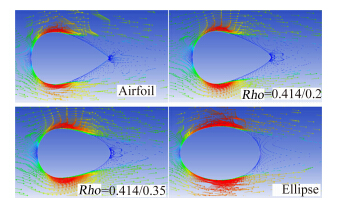 |
| 图 5 剖面速度矢量对比(c/t=1.5) Fig. 5 Comparison of section velocity vector(c/t=1.5) |
非升力剖面一般以升力较小为优,以减小载荷以及对飞机力矩稳定性的影响。4类剖面均为对称剖面零升迎角为0,因此升力特性主要由CLα决定,对比见图 6。从对比可见当c/t>3时翼型剖面具有最大的CLα,标准椭圆的CLα相对翼型剖面降低约17%,变参数椭圆介于二者之间。当c/t<3后,翼型剖面出现CLα<0的现象,相应的速度矢量和压力分布见图 7,可见在小迎角状态下厚翼型的上翼面即出现大面积分离区,而下翼面分离区较小,导致下翼面的负压大于上翼面,产生负升力。
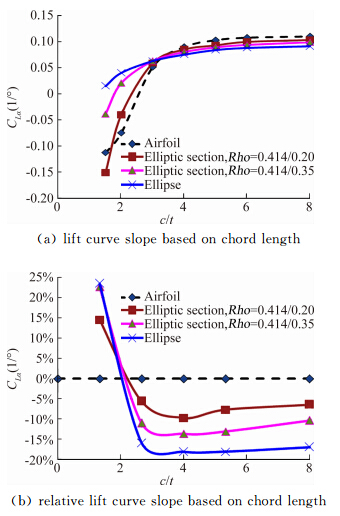 |
| 图 6 剖面升力线斜率对比 Fig. 6 Comparison of section lift curve slope |
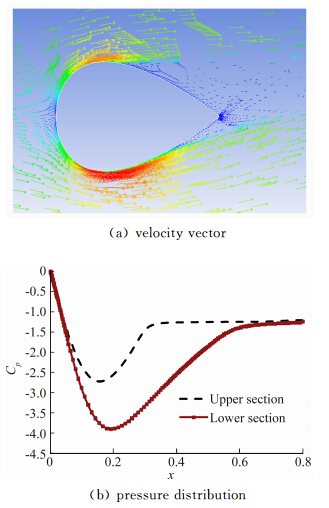 |
| 图 7 长细比c/t=1.5翼型剖面的速度矢量及压力分布(α=6°) Fig. 7 Velocity vector and pressure distribution of airfoil section of c/t=1.5(α=6°) |
翼型剖面、Rho=0.414/0.2剖面当c/t<3后迅速出现较大的负CLα,而后部较丰满的Rho=0.414/0.35剖面和椭圆剖面直到c/t=1.5时CLα量值仍然不大。
3.4 结构特性飞机上的杆状部件根据实际结构形式的不同通常需要承受弯矩和扭矩。承受弯矩的效率正比于剖面厚度,承受扭矩的效率正比于剖面截面积。假设剖面内部结构为前后梁形式,并假设前梁位于15% cA,后梁位于65% cA(对标准椭圆取为25% cA,75% cA),根据几何外形可得到前后梁的高度。剖面截面积不但有利于承受扭矩,同时也有利于满足内部空间的需求,可以采用相对较小的结构尺寸。4类剖面的平均结构高度和截面积相对值见图 8。从对比可见椭圆和Rho=0.414/0.35剖面在结构高度和截面积相对翼型具有7%~14%的优势,而Rho=0.414/0.2剖面与翼型相当。
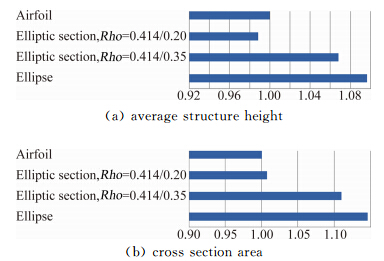 |
| 图 8 剖面结构特性对比 Fig. 8 Comparison of section structure properties |
通过气动和结构特性综合分析来看,对于整流剖面应当采用较厚的剖面以获得最小的阻力,对于翼型剖面可取为c/t=3,进一步降低长细比会出现较大的负CLα;椭圆剖面Rho=0.414/0.2特性与翼型相似,CLα稍小;椭圆剖面Rho=0.414/0.35剖面可取为c/t=2,仍然有较优的升力、阻力特性,且结构高度、截面积相对翼型也有较大提高;标准椭圆剖面整体阻力最大、不易出现负CLα,结构特性较好。采用Rho=0.414/0.35椭圆剖面进行气动整流在小长细比条件下可能具有最优的气动和结构综合效率。
本文的升阻力特性基于定常气动力进行评估,在实际应用时还应通过详细的计算和试验分析确定气流分离的影响。根据具体情况和设计限制,最优的剖面形状和长细比选择也可能出现变化。
| [1] | Hoerner S F,Borst H V.Fluid-dynamic lift 2ed[M].Published by Mrs.Liselotte A.Hoerner,1985:2.6-2.7. |
| [2] | Hoerner S F.Fluid-dynamic drag[M].Published by the author,1965:3.8-3.11. |
| [3] | Kwon K,Park S O.Aerodynamic characteristics of an elliptic airfoil at low Reynolds number[J].Journal of Aircraft,2005,42(6):1642-1644. |
| [4] | Kwon K,Chang B,Lee J,et al.Boundary layers transition measurement over an airfoil by using PIV with high magnification[C]//13th Int Symp on Applications of Laser Techniques to Fluid Mechanics,Lisbon,2006#1191. |
| [5] | Zhan Hao,Deng Yangping,Gao Zhenghong.Investigation on aerodynamic performance of elliptic airfoil at low speed[J].Aeronautical Computing Technique,2008,38(3):26-28.(in Chinese)詹浩,邓阳平,高正红.椭圆翼型低速气动特性研究[J].航空计算技术,2008,38(3):26-28. |
| [6] | Deng Yangping,Gao Zhenghong,Zhan Hao.Experimental investigation on aerodynamics performance of two elliptic airfoils at high speed[J].Journal of Experimental Mechanics,2009,24(2):103-107.(in Chinese)邓阳平,高正红,詹浩.两种椭圆翼型高速气动特性实验研究[J].实验力学,2009,24(2):103-107. |
| [7] | Kwon J,Choi S.Aerodynamic characteristics of elliptic airfoil at high Reynolds number[J].Journal of Aircraft,2008,45(2):641-650. |
| [8] | Chitta V,Dhakal T P,Walters D K.Prediction of aerodynamic characteristics for elliptic airfoils in unmanned aerial vehicle applications[M].Low Reynolds number aerodynamics and transition,Genc M S (Ed.),InTech,2012. |
| [9] | Benazza A,Blanco E,Abidat M.2D detached-eddy simulation around elliptic airfoil at high Reynolds number[J].Journal of Applied Science,7:547-552. |
| [10] | Assel T W.Computational study of flow over elliptic airfoils for rotor/wing unmanned aerial vehicle applications[D].University of Missouri-Rolla,2007. |
| [11] | Ran Hong.Initial investigation of (high) supersonic aerodynamic performance of air vehicle body of elliptic cross-section[C]//Proceedings of 1st contemporary experimental aerodynamics conference,2007:418-424.(in Chinese)冉洪.椭圆截面飞行器单独体(高)超声速气动性能初步研究[C].第一届近代实验空气动力学会议文集,2007:418-424. |
| [12] | Gumusel B,Kavurmacioglu L,Camci C.Aerodynamic drag characteristics and shape design of a radar antenna for airport ground traffic control[C]//ISROMAC-11 Proceedings of the International Symposium on Transport Phenomena and Dynamics of Rotating Machinery,2011. |
| [13] | Raymer D P.Aircraft design:a conceptual approach 4th ed[M].AIAA,2006:132-148. |
| [14] | Ansys,Inc.Ansys Fluent theory guide[M](electronic resource),ANSYS,2011. |
| [15] | Abbott I H,Doenhoff A E.Theory of wing sections[M].Dover Publications Inc,1959:462-463. |


