2. 中国运载火箭技术研究院研发中心, 北京 100076
2. CALT Research & Development Center, Beijing 100076, China
0 引 言
现代高超声速飞行器的发展方向是更远的滑翔距离和优越的机动性能,飞行器的高升阻比是实现上述目标的关键[1]。以升阻比作为单纯的优化指标,设计高升阻比气动布局并不是一件困难的事情。然而工程实际问题是,在满足高升阻比的同时,其他专业开展设计所需要的诸如稳定性和容积空间等性能也能“良好”。传统设计流程中,在根据任务要求达到预期升阻比后,采用 “三轴静稳定”的设计准则,即要求纵向、横向和航向三个通道静稳定(Cmα<0,Clβ<0,Cnβ<0),各自的气动操纵面能够独立满足三个通道的稳定和操纵的要求。在低升阻比高超飞行器的设计上取得了良好结果。但是在高升阻比飞行器的设计上,结果差强人意。表现为飞行器的升阻比提高的同时,稳定性和可操纵性能下降严重,高性能飞行器 “难以操纵”。为了弥合这种矛盾,迫使设计上以降低飞行器的性能以弥补稳定性和操纵性的恶化。维持可用的稳定性和操纵性成为提高飞行器性能的掣肘。这种矛盾是有深刻原因的,是必然伴随高升阻比飞行器的设计[2]。先进高超声速飞行器的设计方法研究,就要解决飞行性能提高的同时,飞行器仍然具有良好的稳定性和操纵性。
 |
| 图 1 高超声速再入飞行器方案(洛玛公司方案和波音公司方案) Fig. 1 Hypersonic entry glide vehicle configuration (Lockheed Martin projection and Boeing projection) |
美国在高超飞行器研制的起步阶段,也是采用三通道静稳定设计方法[3]。始于20世纪50年代的大量高超工程研制实践中,暴露出上述设计方法的局限性。起初,工程界也试图采用腹鳍[4]、翼尖垂尾[5]等补救措施,以牺牲总体性能为代价维持必需的稳定性,实践证明是不成功的。就此开始了先进设计准则的探索工作。1958年,Moul和Paulson[6]针对当时的高超声速滑翔飞行器(hypersonic glider)的布局设计工作,首次提出了Cnβ-dyn和LCDP(Lateral Control Departure Parameter)的概念。基本思想是将横航向作为一个整体考虑,利用通道之间的关联作用,重新定义飞行器的稳定性,突破航向静稳定狭窄的局限。随后在X-2的飞行事故分析中,工程师发现正是因为违反了LCDP稳定性要求,造成了飞行器在向更高马赫数飞行中失去了控制,标志工程界认识到耦合稳定性的工程意义[7],指引了美国高超飞行器气动设计的未来发展方向。1971年,Johnston等人提出第一个关联型和严格化的飞行器失控敏感性判据:Cnβ-dyn-LCDP判据(Bihrle-Weissman判据)[4]。1972年,Weissman在文献[8, 9]中,发展了飞行器失控敏感性判据——Weissman图,采用了飞行器的开环横/航向动态稳定性参数Cnβ-dyn和横向操纵滚转反逆参数LCDP的组合判据,可有效的预测在失速情况下的分离特性和转动特性。这一工作奠定了70年代以后美国高超飞行器设计的理论基础和方法。新理论突破了航向静稳定对飞行器设计的掣肘,扩展了飞行器稳定性设计的可用区域,为获得高性能高超飞行器的设计创造了良好的条件。航天飞机的气动布局是第一个应用的飞行器[4],随后美国的高超声速飞行器的气动布局设计,基本上都依赖于上述理论。近些年来,也在探索新型的其他高超稳定性判据,作为气动布局设计的依据[3, 11, 12, 13, 14, 15, 16, 17],有些方法与Weissman图等价,有些方法还处于学术探索阶段,工程应用的前景不明朗。
目前从公开文献中,可用看到Cnβ-dyn和LCDP判据的表达形式和应用实例,但是公开文献并没有给出判据的应用边界、不同区域对应飞行力学特性,对操稳设计所需资源重新匹配的要求。这些问题不解决,也就无法明确飞行器设计的相关专业需要做出适应新方法的调整,从而不能指导工程设计。日本在这方面有深刻的教训,从20世纪90年代初期开展HOPE-X高超飞行器的气动布局设计,但是直到2001年才掌握先进布局设计方法,对气动布局方案作出重大调整,放弃了此前数年耗费了大量设计资源完成的翼尖垂尾方案,重新开始背双垂尾布局的设计工作[18]。
从21世纪开始,国内的工程界和理论界逐步意识了先进气动布局设计理论的重要性。庄逢甘和张鲁明等[19, 20]在国内首次引入了Weissman图概念,并分析了该方法对高超飞行器设计的意义。吴了泥和黄一敏等在重复使用运载器返回段横侧向控制设计中,采用LCDP和Cnβ-dyn概念开展分析,并明确了上述概念对控制系统设计的物理意义[21]。
目前,工程应用上需要首先回答的是新的稳定定义划分区域的动力学特性,以及同相关设计专业的关联,上述问题如果能够从理论上得到解答,就能够明确先进判据在工程应用上的边界和对相关专业的技术要求,从而构建起应用的整体框架和设计流程。在本文中将采用Cnβ-dyn-LCDP判据的正负极性对飞行器的特性划分为四个区域,然后以某典型飞行器作为研究对象,研究飞行器分别处于三个区域中的典型状态的动力学特性,采用根轨迹法,研究偏航角速率、滚转角速率和侧滑角反馈信号分别单独作用于航向通道和横向通道的响应特性,探讨Cnβ-dyn和LCDP判据划分区域对应的飞行力学特性和反馈响应特性的变化,以明确划分区域的动力性特性和对气动布局设计的指导意义。
1 Cnβ_dyn和LCDP参数介绍Cnβdyn(Dynamic Directional Stability Parameter)和LCDP(Lateral Control Departure Parameter)参数的定义如下:
偏航动态稳定性参数:
横向操纵滚转反逆参数:
Ix和Iy分别表示横向转动惯量和航向转动惯量,Cl和Cn表示滚转力矩和偏航力矩,脚标β表示对应力矩对侧滑角的导数,脚标δr表示副翼操纵引起对应力矩导数。关于上述参数的物理意义,可以参见文献[19, 21],这里不详细介绍。
需要指出的是,参数的具体表达形式和极性同坐标系密切相关。在本文中,将采用x朝前,y轴对称面朝上的坐标系,横航向的静稳定导数为负表示稳定。偏航动态稳定性参数反应了飞行器绕速度矢量的航向稳定性,小于零表示稳定,大于零不稳定;后者表示横向通道在副翼操纵下的响应极性,判据考虑到了横航向静稳定性的影响。
在本文的坐标系中,两者极性的划分都是以正负进行区分。这样我们在飞行器特性上就可以得到如下四个状态:
Cnβ_dyn<0、 LCDP<0
Cnβ_dyn<0、 LCDP>0
Cnβ_dyn>0、 LCDP<0
Cnβ_dyn>0、 LCDP>0
这四个状态的稳定性的划分,反馈作用下的响应特性,对飞行器气动布局设计的意义,将是本文的研究重点。
2 分析对象和分析方法本文以类似图 1洛玛公司方案的高超飞行器作 为分析对象,以前叙的划分方式,开展对应的横航向通道的模态和闭环特性的分析。采用基于瞬时平衡化的小偏差横航向方程作为分析的动力学模型:
其中,g重力加速度,V飞行速度,σ弹道偏角,β侧滑角,γ滚动角,θ弹道倾角,ψ偏航角,ω表示绕飞行器的角速度,脚标表示转动的轴,δ表示舵偏转动角,脚标ψ表示方向通道,γ表示滚动通道。c和b表示对应脚标的系数。
根据Cnβ_dyn和LCDP参数的正负,将对象划分四种状态。该布局的全部特性只存在三种状态,各自选取一个代表作为分析对象(表 1)。该三个特征点的分布给出在图 2 中。Cnβ_dyn>0、LCDP<0状态在该飞行器的气动特性数据库中不存在,事实上此状态在布局设计上出现的可能性比较小,后面会给出说明。
 |
| 图 2 特征点的Cnβ_dyn-LCDP联合分布 Fig. 2 Characteristic points for Cnβ_dyn-LCDP joint distribution |
| 状态1 | Ma=4,α=2° | Cnβ_dyn<0、 LCDP<0 |
| 状态2 | Ma=10,α=10° | Cnβ_dyn<0、 LCDP>0 |
| 状态3 | Ma=20,α=2° | Cnβ_dyn>0、 LCDP>0 |
图 3~图 5依次给出上述三个状态的横航向模态的分布图。从图中可以看出,横航向运动可能存在一对短周期振荡模态(荷兰滚模态)、一个短周期单调模态(快速滚转模态)和一个长周期单调模态(螺旋模态)。
 |
| 图 3 状态1的横航向模态 Fig. 3 Directional-lateral mode for status 1 |
 |
| 图 4 状态2的横航向模态 Fig. 4 Directional-lateral mode for status 2 |
 |
| 图 5 状态3的横航向模态 Fig. 5 Directional-lateral mode for status 3 |
从上面的分析可以看出:
(1) 当Cnβdyn<0,LCDP<0时,横航向具有三个模态:一个稳定长周期单调模态、一个稳定短周期单调模态、一对稳定振荡模态。
(2) 当Cnβdyn<0,LCDP>0时,横航向具有三个模态:一个稳定长周期单调模态、一个稳定短周期单调模态、一对不稳定振荡模态。
(3) 当Cnβdyn>0,LCDP>0时,横航向具有四个模态:两个稳定长周期单调模态、一个稳定短周期单调模态、一个不稳定单调模态。
3 单通道反馈作用下的闭环特性上一章节分析了飞行器三个典型状态的开环特性。在本章节中,将分析三个典型状态的闭环特性,通过反馈提高阻尼和稳定性。通常横航向的反馈信号包括:偏航角速率、滚转角速率和侧滑角信号,这些反馈信号可以分别单独作用于航向通道和横向通道,因此总共会有6种类型。下面将采用根轨迹法,依次分析各种反馈类型下飞行器模态特性的变化。
3.1 偏航通道反馈偏航角速率 →Δδψ
→Δδψ
偏航通道反馈偏航角速率是经典的反馈方式,能够有效实现增稳。三个典型状态应用偏航通道反馈偏航角速率依次给出在图 6~图 8中可知:
 |
图 6  →Δδψ时根轨迹图(状态1)
Fig. 6 Root locus diagram for →Δδψ时根轨迹图(状态1)
Fig. 6 Root locus diagram for  →Δδψ feedback(status 1) →Δδψ feedback(status 1) |
 |
图 7  →Δδψ时根轨迹图(状态2)
Fig. 7 Root locus diagram for →Δδψ时根轨迹图(状态2)
Fig. 7 Root locus diagram for  →Δδψ feedback(status 2) →Δδψ feedback(status 2) |
 |
图 8  →Δδψ时根轨迹图(状态3)
Fig. 8 Root locus diagram for →Δδψ时根轨迹图(状态3)
Fig. 8 Root locus diagram for  →Δδψ feedback(status 3) →Δδψ feedback(status 3) |
对于状态1,引入偏航角速率反馈后可以使得短周期振荡模态远离虚轴,靠近实轴,从而提高短周期振荡模态的频率和阻尼,但是短周期单调模态和长周期单调模态均向虚轴靠近,稳定性降低。
对于状态2,引入偏航角速率反馈后可以使得不稳定振荡模态进入左半平面实现稳定,短周期单调模态远离虚轴,稳定性提高,长周期单调模态远离虚轴,稳定性提高。
对于状态3,引入偏航角速率反馈后不能使得不稳定单调模态进入左半平面实现稳定。
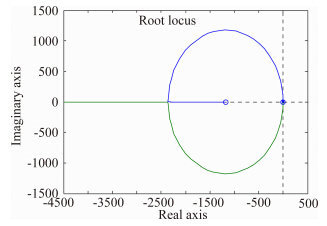
3.2 偏航通道反馈侧滑角Δβ→Δδψ偏航通道反馈侧滑角也可以实现增稳。三个典型状态应用偏航通道反馈侧滑角的根轨迹图给出在图 9~图 11中可知:
 |
| 图 9 Δβ→Δδψ时根轨迹图(状态1) Fig. 9 Root locus diagram for Δβ→Δδψ feedback(status 1) |
 |
| 图 10 Δβ→Δδψ时根轨迹图(状态2) Fig. 10 Root locus diagram for Δβ→Δδψ feedback(status 2) |
 |
| 图 11 Δβ→Δδψ时根轨迹图(状态3) Fig. 11 Root locus diagram for Δβ→Δδψ feedback(status 3) |
对于状态1,引入侧滑角角反馈可以增大短周期振荡模态的频率,短周期振荡模态的阻尼逐渐增大,但是,要取得明显的效果需要较高的反馈增益。
对于状态2,引入侧滑角角反馈可以使得不稳定振荡模态进入左半平面实现稳定,短周期单调模态靠近虚轴,稳定性降低,长周期单调模态变化不大,但是,要取得明显的效果,需要较高的反馈增益。
对于状态3,引入侧滑角角反馈可以使得不稳定单调模态进入左半平面实现稳定,长短周期单调模态逐渐变为一对振荡模态,但是,要取得明显的效果,需要较高的反馈增益。
可以注意到状态1与状态2根轨迹特性类似,说明该通道反馈拓扑结构与Cnβ-dyn的正负关系密切。反馈侧滑角到方向舵不能明显改善航向稳定性,尽管最终能够使得振荡模态趋于稳定,但是增稳所需增益非常大,在工程上是无法实现的。
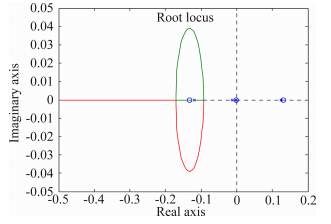
3.3 滚动通道反馈滚动角速率Δωx1→Δδγ通常滚转通道反馈滚动角速率用来增强滚转操纵响应性能,这是传统的设计思路。但是在高超声速下该增稳通道却存在独特的根轨迹拓扑结构。三个典型状态应用滚动通道反馈滚动角速率依次给出在图 12~图 14中可知:
 |
| 图 12 Δωx1→Δδγ时根轨迹图(状态1) Fig. 12 Root locus diagram for Δωx1→Δδγ feedback(status 1) |
 |
| 图 13 Δωx1→Δδγ时根轨迹图(状态2) Fig. 13 Root locus diagram for Δωx1→Δδγ feedback(status 2) |
 |
| 图 14 Δωx1→Δδγ时根轨迹图(状态3) Fig. 14 Root locus diagram for Δωx1→Δδγ feedback(status 3) |
对于状态1,引入滚动角速率反馈后存在一对二阶零点,与振荡模态靠近,因而反馈增稳后对于振荡模态的影响不大,同时单调稳定模态的稳定性随反馈增益明显改善,从而增强了滚转操纵的响应特性。
对于状态2,引入滚动角速率反馈可以使得不稳定的荷兰滚模态勉强进入左半平面实现稳定,不过增益很大,短周期单调模态远离虚轴,稳定性提高,长周期单调模态影响不大。
对于状态3,引入滚动角速率反馈不能使得不稳定振荡模态进入左半平面实现稳定。
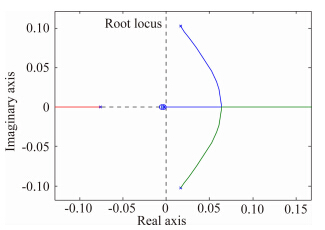
3.4 滚动通道反馈侧滑角Δβ→Δδγ通过滚动通道反馈侧滑角实现增稳。三个典型状态应用滚动通道反馈侧滑角依次给出在图 15~图 17中可知:
 |
| 图 15 Δβ→Δδγ时根轨迹图(状态1) Fig. 15 Root locus diagram for Δβ→Δδγ feedback(status 1) |
 |
| 图 16 Δβ→Δδγ时根轨迹图(状态2) Fig. 16 Root locus diagram for Δβ→Δδγ feedback(status 2) |
 |
| 图 17 Δβ→Δδγ时根轨迹图(状态3) Fig. 17 Root locus diagram for Δβ→Δδγ feedback(status 3) |
对于状态1,引入侧滑角反馈使得稳定振荡模态进入右半平面变得不稳定。
对于状态2,引入侧滑角反馈不能使得不稳定振荡模态进入左半平面实现稳定。
对于状态3,引入侧滑角反馈不能使得不稳定振荡模态进入左半平面实现稳定。
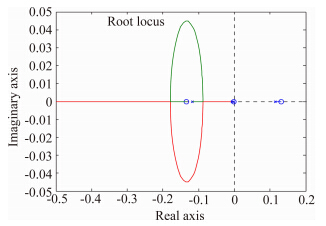
3.5 偏航通道反馈滚动角速度Δωx1→Δδψ通过偏航通道反馈滚动角速率实现增稳。三个典型状态的偏航通道反馈滚动角速率的根轨迹图依次给出在图 18~图 20中可知:
 |
| 图 18 Δωx1→Δδψ时根轨迹图(状态1) Fig. 18 Root locus diagram for Δωx1→Δδψ feedback(status 1) |
 |
| 图 19 Δωx1→Δδψ时根轨迹图(状态2) Fig. 19 Root locus diagram for Δωx1→Δδψ feedback(status 2) |
 |
| 图 20 Δωx1→Δδψ时根轨迹图(状态3) Fig. 20 Root locus diagram for Δωx1→Δδψ feedback(status 3) |
对于状态1,引入滚动角速率反馈虽然可以增强长周期滚动模态的稳定性,但是,并不能增强荷兰滚模态的稳定性,随着增益增大将进入到右半平面。
对于状态2,引入滚动角速率反馈可以使得不稳定的荷兰滚模态进入左半平面实现稳定,但是,长周期单调模态将向虚轴靠近进入右半平面,导致系统不稳定。
对于状态3,引入滚动角速率反馈不能使得不稳定单调模态进入左半平面实现稳定。
3.6 滚动通道反馈偏航角速度Δωy1→Δδγ通过滚转通道反馈偏航角速率实现增稳。三个典型状态的滚转通道反馈偏航角速率的根轨迹图依次给出在图 21~图 23中可知:
 |
| 图 21 Δωy1→Δδγ时的根轨迹图(状态1) Fig. 21 Root locus diagram for Δωy1→Δδγ feedback(status 1) |
 |
| 图 22 Δωy1→Δδγ时的根轨迹图(状态2) Fig. 22 Root locus diagram for Δωy1→Δδγ feedback(status 2) |
 |
| 图 23 Δωy1→Δδγ时的根轨迹图(状态3) Fig. 23 Root locus diagram for Δωy1→Δδγ feedback(status 3) |
对于状态1,引入偏航角速率反馈使得短周期振荡模态远离虚轴,靠近实轴,从而提高短周期振荡模态的频率和阻尼,但是短周期单调模态和长周期单调模态均向虚轴靠近,稳定性降低。
对于状态2,引入偏航角速率反馈可以使得不稳定振荡模态进入左半平面实现稳定,但是短周期单调模态接近虚轴,稳定性降低。
对于状态3,引入偏航角速率反馈不能使得不稳定单调模态进入左半平面实现稳定。
4 闭环特性的综合分析三种典型状态自身的模态特性和反馈作用下响应的差异性,表明Cnβ-dyn和LCDP参数是能够比较准确刻划飞行器的性能。采用本方法也分析过其他高超飞行器,根轨迹的拓扑结构基本一致,飞行器外形变化不会影响主要结论。两个参数的表达形式简单,应用简便,符合作为布局方案设计的判据的使用要求。
按照传统的航向静稳定性的要求开展高超声速气动布局设计,主要采取增大方向舵的面积或增加迎风腹鳍等措施,这是以牺牲飞行器的升阻比为代价。而高超飞行器往往出于减小热流的目的,会要求保持大攻角飞行,此时方向舵将处于背风区,航向稳定性会随着攻角的增加,大幅度下降。因此高超飞行器设计中,提高航向静稳定性是一个非常困难的事情。采用Cnβ-dyn判据后,从飞行器Cnβ-dyn分布图就可以看到,由于飞行器一般都能获得良好的横向静稳性,滚转通道的静稳定性可以弥补航向静稳定性的不足。因此Cnβ-dyn相对于传统的航向静稳定性设计判据是一个更加宽松的设计判据,放宽了航向静稳定性的要求,一定程度的航向静不稳定也可以接受,这样飞行器的气动布局设计环境变得宽松。采用Cnβ-dyn判据,可以看到飞行器的航向稳定性几乎不是问题,对于大攻角尤是如此。
 |
| 图 24 飞行器航向静稳定分布 Fig. 24 Weathercock stability characteristic for hypersonic vehicle |
Cnβ-dyn的分布对荷兰滚模态有着深刻的影响。只要Cnβ-dyn稳定,即使开环的荷兰滚模态不稳定,也可以通过适当的闭环反馈稳定。从上述的闭环分析,航向通道的航向速率、滚转速率和侧滑角反馈可以使得荷兰滚模态进入左半平面稳定,并能改善阻尼。滚转通道的反馈对于改善短周期单调模态(快速滚转模态)有着正面的影响。
在保证Cnβ-dyn稳定的条件下,一定程度的滚转反逆可以通过合适的反馈进行增稳。因此,在相应提高控制系统设计要求的条件下,可以允许气动布局设计上出现适度的滚转反逆。选择合适的闭环反馈使得布局可控。这样就进一步放宽了气动布局设计的限制性条件。
当然当飞行器出现滚转反逆情况时候,会给飞行器设计造成较大影响,需要小心应对。如果飞行器在全程弹道中,LCDP的极性不发生变化,均是稳定或不稳定,控制系统设计上不存在太大困难。但是实际的高超飞行器,由于跨越马赫数范围和高度范围太广,很难保证全程LCDP不发生反号问题。
当在飞行弹道中出现LCDP极性变化时候,意味着飞行器的滚转控制会出现“反向操纵”。美国航天飞机在在方案阶段尝试过在LCDP变号处通过控制系统极性反号来解决极性问题,但是最终还是放弃了该方案[6]。因为由于气动特性存在误差,无法准确的给出极性变化的时刻,这样控制系统做出切换时机的判断非常困难,系统存在失控的危险。
Cnβ-dyn和LCDP同时不稳定的情况,通过上述分析可以看到,模态有着完全不同的拓扑结构,蜕化后的不稳定单调模态趋于非最小相位零点,从而系统更加不稳定。单独反馈无法有效提高模态稳定性。Cnβ-dyn和LCDP同时不稳定的气动布局,会给稳定设计和控制系统设计造成巨大困难,在目前的设计能力下,几乎是无法克服的困难。因此,在气动布局设计初期和总体的小回路设计阶段,要剔除掉这样的飞行状态,不允许上述的飞行状态出现。
5 总 结针对新一代高超飞行器性能越来越高的要求,需要发展新型的气动布局设计判据,以摆脱性能提高和操纵性下降之间的恶性关系。力求建立一种新型的能够满足气动布局设计和总体小回路设计需求的简单、实用和具有可操纵性的设计判据。通过对典型飞行器不同Cnβ-dyn和LCDP特性的横航向开环和闭环模态特性划分,研究了根轨迹的特性,探索上述参数作为新型气动布局设计判据的可行性。通过初步的分析,得到:
Cnβ-dyn能够做为一种比单通道稳定性判据的Cnβ更加宽松的航向布局航向稳定性设计准则,而LCDP的极性可以做为滚转控制性能的选择参数,两者共同划分飞行器的性能,作为方案阶段气动布局设计的依据。
下一步还将开展深入的研究工作,进一步讨论区域划分对控制特性的影响,探讨重力因素、动压等多重因素对飞行器稳定边界的影响,开展多重反馈作用和舵面联合控制作用下的闭环模态特性,探索解决滚转操纵反逆的设计新方法。
| [1] | Phillips T H.A common aero vehicle (CAV) model,description,and employment guide[R].Schafer Corporation for AFRL and AFSPC,2003 |
| [2] | Zhang Luming,Ye Youda,et al.Analysis for space shuttle aerodynamics[M].Beijing:National Defence Industry Press,2009.(in Chinese)张鲁民,叶友达,等.航天飞机空气动力学分析[M].北京:国防工业出版社,2009. |
| [3] | Seltzer R M.Investigation of current and proposed aircraft departure susceptibility criteria with application to future fighter aircraft[R].NADC-90048-60,1990 |
| [4] | Day R E.Coupling dynamics in aircraft:a historical perspective[R].NASA SP-532,1997 |
| [5] | Spearman M L.Aerodynamic characteristics of some lifting reentry concepts applicable to transatmospheric vehicle design studies[R].AIAA-84-2146,1984. |
| [6] | Moul M T,Paulson J.Dynamic lateral beravior of high-performance aircraft[R].NACA RML58EE,Aug,1958. |
| [7] | Whitford R.Lessons learned from the bell X-2 program[R].AIAA-97-5524,1997. |
| [8] | Weissman,Development of disign criteria for perdicting departure characteristics and spin susceptibility of fighter-type aircraft[R].AIAA-72-984,1972. |
| [9] | Weissman,Status of design criteria for predicting departure characteristics and spin susceptibility[R].AIAA-74-791,1974. |
| [10] | Tang Wei,Feng Yi,Ning Yong,et al.Aerodynamics configuration conceptual design for X-38 analog lifting body transporter[J].Acta Aerodynamica Sinica,2011,29(05):555-558.(in Chinese)唐伟,冯毅,宁勇,等.类X-38升力体运载器气动布局概念设计[J].空气动力学学报,2011,29(05):555-558. |
| [11] | Kalviste,Aircraft stability characteristics at high angles of attack[C]//AGARD Conference Proceedings,No.235,May 1978. |
| [12] | Kalviste,Copled static and dynamic stability parameters[R].AIAA-83-2069,1983. |
| [13] | Chody,Combat aircraft control requirements for agility[R].AGARD CP-465,Oct.1989. |
| [14] | Lutze F H.Development of lateral-directional departure criteria[R].AIAA-93-48301,1993. |
| [15] | Rafael Livneh.Improved literal approximation for the lateral-directional dynamics of rigid aircraft[R].AIAA-95-3307-CP,1995 |
| [16] | Brijesh Raghavan,Ananthkrishnan N.Small-perturbation analysis of airplane dynamics with dynamic stability derivatives refined[C]//AIAA Atmospheric Flight Mechanics conference and Exhibit,15-18 August 2005. |
| [17] | Lee B,Zaichik L,Yashin Y,et al.Criterion to estimate optimum lateral static stability margin[C]//AIAA Atmospheric Flight Mechanics conference and Exhibit,20-23 August 2007. |
| [18] | Takeshi Tsujimoto,Yasuro Sakamoto,Toshio Akimoto,et al.Aerodynamic characteristic of HOPE-X configuration with twin vertical tails[R].AIAA 2001-1827. |
| [19] | Zhu Liguo,Wang Yongfeng,Zhuang Fenggan,et al.The lateral-directional departure criteria analysis of high-speed and high maneuverability aircraft[J].Journal of Astronautics,2007,28(6):1550-1553.(in Chinese)祝立国,王永丰,庄逢甘,等.高速高机动飞行器的横航向偏离预测判据分析[J].宇航学报,2007,28(26):1550-1553. |
| [20] | Zhu Liguo,Wang Yongfeng,Zhuang Fenggan,et al.The derivation,development of weissman chart and applications on configuration design of reentry vehicle[J].Journal of Astronautics,2009,30(1):13-17.(in Chinese)祝立国,王永丰,庄逢甘,等.Weissman图的产生、发展及其在再入航天飞行器气动布局设计中的应用[J].宇航学报,2009,30(1):13-17. |
| [21] | Wu Liaoni,Huang Yimin,He Chenglong.Reusable launch vehicle lateral control design of glide return phase[J].Journal of Nanjing University of Aeronautics&Astronautics,2009,41(3):329-333.(in Chinese)吴了泥,黄一敏,贺成龙.重复使用运载器返回段横侧向控制系统[J].南京航空航天大学学报,2009,41(3):329-333. |





