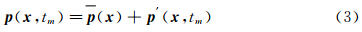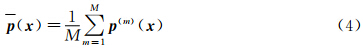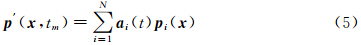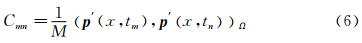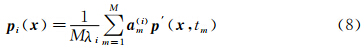0 引 言
大型运输类飞机上多采用超临界翼型，以达到增加阻力发散马赫数的目的。但是在跨声速范围内机翼有可能会产生由激波/附面层相互干扰而引起的跨声速抖振现象，这将严重影响飞行器的飞行品质与结构寿命[1]，因此对于跨声速抖振问题的研究就显得非常重要。
为了对由激波/附面层干扰而产生的跨声速抖振现象进行深入研究，法国国家航空航天科研局(ONERA)于2005年对OAT15A超临界翼型的二维翼段进行了风洞实验[2, 3]。由于L. Jacquin[2, 3]等使用OAT15A模型进行的实验比以往同类实验提供了更加丰富详尽的实验条件说明与结果分析，所以很多研究者将其作为研究跨声速激波抖振现象的标准算例[4, 5, 6]。
除了对于OAT15A翼型的研究之外，近期对于抖振现象的研究还包括新的抖振边界预测方法[7, 8]、抖振强度的控制方法[9, 10]以及更接近于实际情况的抖振现象的研究[11]。
本征正交分解POD方法是一种将数据进行压缩的多变量统计分析方法，其基本思想是根据已有样本数据计算得到一组最能够代表这组数据的正交基函数，即使得样本数据投影到此正交基上所产生的误差最小。在构造这组基函数时使得样本数据在正交基上的投影分量按次序依次迅速衰减[12]，所以它可以将高维数据降阶投影到低维空间，从而获得数据的物理特征[13]。该方法已经被广泛应用于建立流场的降阶模型[14]、翼型的反设计[15]以及流动结构分析[16, 17, 18]等方面。
本文使用结构化网格，针对风洞实验状态条件进行了OAT15A超临界二维翼型绕流的抖振问题CFD数值方法研究。在比较了不同网格分布对于计算结果的影响之后，选择其中一套网格的计算结果进行了相应的后处理并深入的研究了抖振现象的发展过程，发现激波运动的相位与升力系数波动的相位并不完全相同。接下来提取了流场结果的POD模态，从物理流动相干流场结构角度对抖振现象进行了分析，寻找抖振现象的主导模态。
1 跨声速抖振流场的模拟及分析 1.1 算例描述及数值方法L. Jacquin[2, 3]等人对于OAT15A翼型在马赫数为0.73，来流迎角为3.5°，雷诺数为3×106的实验条件下所获得的结果进行了比较全面的分析，因此选择此实验条件作为数值模拟的条件。这个实验条件下的结果也是大多数研究者进行数值模拟时所选用的对比结果[2, 3, 5, 6]。
使用基于有限体积法的流场解算程序进行数值模拟，空间离散格式为二阶迎风Roe格式[19]，时间项则采用全隐式双时间格式[20]，物理时间步长为6.6×10-5s，并使用当地时间步长[21]来提高计算效率，湍流模型选用S-A一方程模型[22]。
1.2 网格收敛性练习本文划分了疏密不同的三套网格。三套网格均为O型网格，远场半径为50倍参考弦长，近壁面第一层网格满足y+<1，且翼型前缘节点分布也完全相同。这三套网格不同之处主要有两点：一是翼型钝后缘处的网格节点数目依次为6、10、30；二是后缘之后的气流分离区范围之内的网格的疏密不同，其中B网格的后缘网格最稀疏。第一套网格中翼型周围的网格如图 1所示，三套网格的参数如表 1。
 |
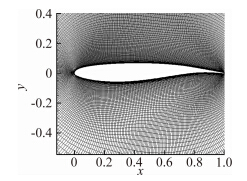| 图 1 A网格的网格拓扑结构 Fig. 1 Grid topology for Mesh A |
| Mesh | Grid points | Grid cells |
| A | 458×124 | 56211 |
| B | 517×115 | 58938 |
| C | 628×116 | 72105 |
使用这三套网格计算出的升力系数随时间的变化如图 2所示。从图中可以看到使用A与C网格计算出了周期性的升力系数波动，其波动的幅度相近，而B网格对应的升力系数则最终收敛于一个定值。结合三套网格的不同之处来看，B网格无法计算出抖振现象的主要原因就是其在后缘之后弦向网格分布均匀的区域过小。
 |
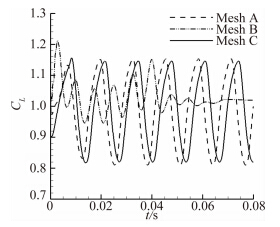| 图 2 升力系数随时间的变化 Fig. 2 Lift coefficient evolution versus time |
截取A与C网格升力系数波动的周期性部分并进行傅里叶变换(FFT)，就得到了这两套网格计算出的抖振频率，分别为77.8Hz与76Hz，而实验值为69Hz，C网格频率的计算值更加接近于实验值。将计算得到的平均压力系数、压力均方根值与实验值以及文献[6]中使用KKL湍流模型的计算值进行对比，分别如图 3和图 4，可以看到A、C两套网格的计算值几乎重合。本文计算出的平均压力系数在整个下表面以及上表面超声速区与实验值吻合程度较好，而在激波运动区域与再压缩区则与实验值则有一定偏差，文献[5]使用KKL模型计算出的激波运动范围与实验值相比整体靠后；均方根值的幅度高于实验值，但本文均方根值突增的起始位置与实验相同，使用KKL模型得到的波动范围较窄。
 |
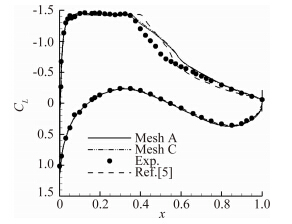| 图 3 翼型表面平均压力系数 Fig. 3 Mean surface pressure coefficient distributions |
 |
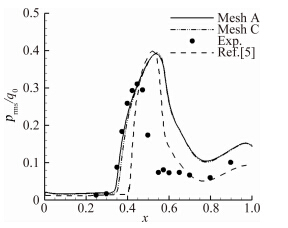| 图 4 翼型上表面压力均方根值分布 Fig. 4 Pressure rms distributions on the top side of OAT15A airfoil |
激波的平均位置可以通过压力脉动偏斜因子[2]的分布得到，其定义如下：
式中，p′为压力的脉动量，即p′=p(t)－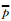
，p(t)为每一瞬时的压力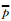，为压力的时均值。压力脉动偏斜因子考虑了压力脉动在一个周期之中的时间分布以及脉动量的绝对大小。其值为正，说明压力在一个周期中的大部分时间内要小于平均值；其值为负，说明压力在一个周期之中的大部分时间内要大于压力的平均值；这个值的绝对值越大，则表示在某个或某些时刻时压力偏离压力平均值的量越大。
上表面Sp的计算值与实验值沿弦向的分布如图 5。在激波运动区域之内，Sp出现最大值，并在之后迅速衰减至最小值。这两个值对应于激波震荡时上游与下游的极限位置，而其间Sp为零的点所对应的弦向位置就是激波的平均位置。两套网格的激波运动区域介于0.35c至0.6c之间，大于实验值测得的0.35c至0.5c的范围。计算出的激波平均位置在0.5c处，比0.44c的实验值靠后。由于采用的URANS方法对于小脉动量的模拟能力有所不足，造成压力均方根和压力脉动偏斜因子的计算值与实验值有一定的差距。
 |
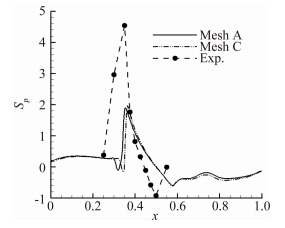| 图 5 翼型上表面Sp沿弦向的分布 Fig. 5 Sp distributions on the top side of OAT15A airfoil |
综上所述，选择C网格的瞬时计算结果作为分析数据。
1.3 抖振流场的非定常结果分析压力脉动偏斜因子可以描绘出激波在一个周期之中的移动范围和平均位置，但是却不能反映其随时间的变化历程。瞬时激波位置Xsh的变化曲线与升力系数波动曲线对比如图 6。从图中可以看到，使用上述方法计算出的激波位置运动的范围与通过平均压力系数和压力脉动因子所推测的范围基本一致，能够大致的描绘出激波在抖振中移动规律。通过FFT变换计算得到激波位置移动的频率为76Hz，与升力系数的波动频率一致，其相位角比升力系数波动的相位角略微靠前。这表明激波的移动与翼型升力系数的波动有很强的关联，但是这两者之间有大约30°的相位差。
 |
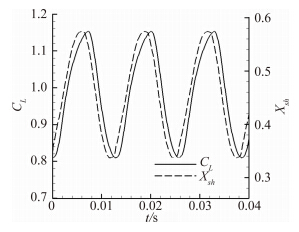| 图 6 激波位置与升力系数在相同时间内的波动 Fig. 6 Shock location Xsh and lift coefficient evolution in the same period |
分别截取一个周期之内不同时刻的马赫数云图如图 7，对应的翼型尾缘附近流线如图 8，这几个时刻在一个升力系数波动周期之中的位置如图 9所示。其中(a)对应于激波位置在最下游的时刻，(b)对应于升力系数波动曲线的波峰时刻，(c) 为从激波最下游位置到最上游位置之间的一个时刻，(d)对应于激波位置处于最上游的时刻，(e)对应于升力系数曲线波动的波谷时刻，(f)为从波激波最上游位置到最下游 位置之间的一个时刻。在(a)时刻，激波位于一个抖振周期之中最下游的位置，翼型上表面激波根部有一个小的分离气泡，这使附面层增厚，进而导致翼型的有效弯度减小，激波按着从(a)-(b)-(c)-(d)的顺序大幅向上游移动，同时分离区逐渐增大，直至到达激波在抖振周期中的最上游位置(d)，在此期间激波的强度也相应的增大；在位置(d)处分离区的范围最大，而从此时开始激波开始按照(d)-(e)-(f)-(a)的顺序沿机翼表面向下游移动，同时激波的强度减弱，其中按照 (d)-(e)-(f)的顺序分离区逐渐减小直至机翼上表面的气流分离区完全消失，可以看到在(e)时刻，翼型上表面的激波根部与翼型后缘处同时存在两个分离气泡，这说明在分离区消失的过程中，首先是整个分离区的范围减小直到分成了激波根部与后缘处两个分离区，然后这两个分离区逐渐减小，上表面接近后缘的分离区完全消失，而从(f)-(a)的过程中，准确的说是在(a)之前的某一时刻则机翼上表面产生出了一个小的分离气泡；另外，升力系数波峰与波谷所处的时刻(b)和(e)出现的时刻都略微滞后于激波在最下游与最上游的时刻(a)和(d)。
 |
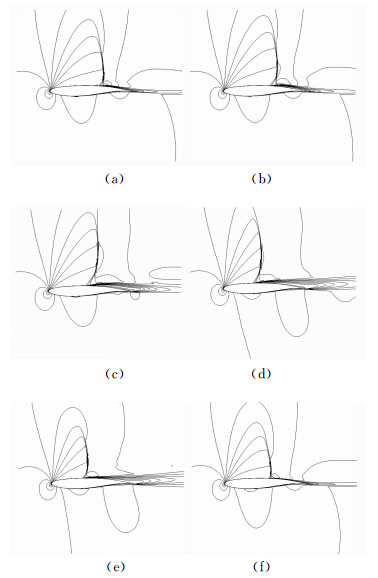| 图 7 一个激波震荡周期之内不同时刻的马赫数云图 Fig. 7 Contours of Mach number at different instant time during one cycle of flow oscillation |
 |
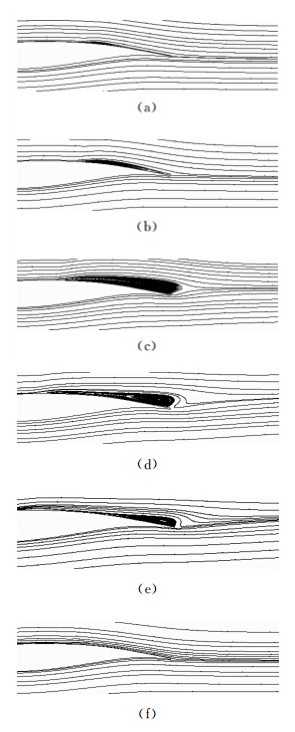| 图 8 一个激波震荡周期之内不同时刻的尾缘附近的流线 Fig. 8 Streamlines near the tailing edge at different instant time during one cycle of flow oscillation |
 |
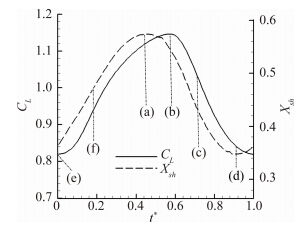| 图 9 马赫数云图对应的时刻在一个升力波动周期中的位置(t*=t/T，T为波动周期) Fig. 9 Instant times at which the Mach number contours are intercepted in one lift fluctuation cycle (t*=t/T,T is the fluctuation period) |
以提取静压的POD模态为例，按照相同的时间间隔tm得到M份快照：
式中：m=1,2,…,M。
压力场可以分解为平均流动分量和瞬时波动分量：
式中：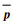
(x)是平均流动分量，p′(x,t)是瞬时波动分量。
使用POD方法就可以将p′(x,t)化为如下形式：
式中：pi(x)是i阶POD基函数，时间变化特性通过第i阶模态的时间系数ai(t)表现出来。
定义M×M阶自相关矩阵C，其中每一个元素Cmn如下：
式中：m,n=1,2,…,M，下标Ω表示在整个的空间域进行积分。
为了获得出第i个模态的时间系数向量a(i)，需要求解如下的特征值问题
式中：特征值λi代表了流场投影在第i阶基函数pi(x)上的平均“能量”。相关系数矩阵的特征向量就是时间系数向量a(i)=(a1(i),a2(i),…,aM(i))。
按照正实特征值由大到小的顺序为模态进行排序，即λ1≥λ2≥λ3≥…>0；特征值为零的模态对速度场无影响，所以将其去掉。由于自相关矩阵C是自伴随矩阵并且是半正定的，所以时间系数相互正交。可以得到POD模态如下：
使用快照方法在时域中进行POD分解，则其产生的相关系数矩阵的规模为M×M；而如果在空间域进行POD分解，则其关系数矩阵的规模为Ng×Ng，Ng为网格点的数目。可见，快照方法更适用于处理大量的CFD计算数据。
2.2 OAT15A翼型抖振流场的POD分析为了提取抖振流场静压分布的POD模态，使用C网格的280个瞬时流场结果作为“快照”，确保其包含的时间长度大于一个周期，并将计算出的压强除以的远场压强得到无量纲压强。提取的前六阶POD模态每个模态的特征值占全部特征值的百分比以及前n阶特征值之和占全部特征值的百分比如表 2，前50阶模态特征值的衰减如图 10所示。可以看到第一阶与第二阶模态的特征值占全部模态特征值的比重最大，这两者的大小相近，其它阶模态的特征值相对较小，且从第三阶模态开始特征值衰减的速率就开始减缓。如前所述，模态特征值的大小表征了此阶模态“能量”所占系统总“能量”的大小，所以可以认为第一阶模态与第二阶模态在抖振现象中占主导地位。
 |
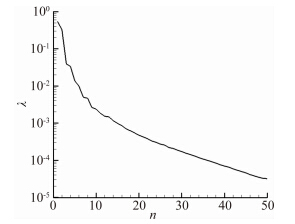| 图 10 前50阶模态特征值的变化曲线 Fig. 10 The eigenvalue attenuation of the first fifty modes |
| Mode number n |  |  |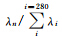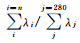
| 1 | 54.67% | 54.67% |
| 2 | 32.74% | 87.41% |
| 3 | 3.91% | 91.32% |
| 4 | 3.37% | 94.70% |
| 5 | 1.38% | 96.07% |
| 6 | 0.99% | 97.06% |
计算得到的流场静压的第一阶、第二阶模态如图 11。可以看到第一阶模态包含了激波运动与由其产生的气流分离，其中尤以激波根部与附面层之间相互作用的区域最为显著；第二阶模态则主要与气流分离有关。
根据公式(5)可知，流场中压力的波动值为计算所得的每一阶的模态值乘上同一时刻的时间系数再求和，时间系数为无量纲值。计算得到的前六阶模态的时间系数随时间的变化如图 12，可以看到第一阶模态与第二阶模态的时间系数的波动幅度最大，与其它模态的时间系数相比占主导地位；且随着模态阶数的提高，模态的时间系数的幅值越来越小、频率越来越高并更加不规则；第一阶模态与第二阶模态的时间系数频率均为76Hz，与升力系数波动的频率一致，可以认为抖振现象主要为第一阶模态和第二阶模态合成的结果。另外，第一阶模态的时间系数波动的波峰值与第二阶模态的波峰值之间大概相差四分之一周期，也就是说第一阶模态滞后于第二阶模态90°的相位，这是由POD模态的正交性所决定的。
 |
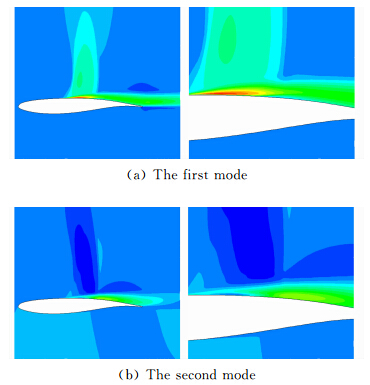| 图 11 第一阶与第二阶POD模态云图 Fig. 11 Contours of the first and the second POD modes |
 |
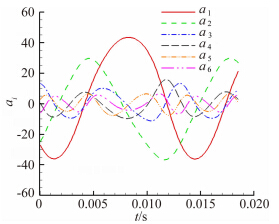| 图 12 前六阶模态的时间系数随时间的变化 Fig. 12 Evolution of temporal coefficients of the first six mode |
将第一阶、第二阶模态的时间系数与相同时间内升力系数的波动在同一副图中比较，如图 13，其中第一阶模态的时间系数的相位角要比升力系数的相位角超前大约30°，与激波位置的相位角十分接近，说明第一阶模态主要表征了激波运动对压力分布的影响。由于这些模态都对应于实际的空间结构，那么这也从另一个方面表明第二阶模态主要表征了翼型上表面的气流分离。
 |
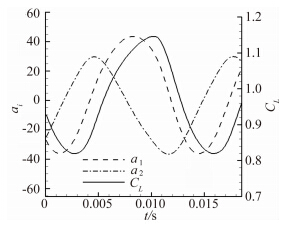| 图 13 前两阶模态的时间系数与相同时间内的升力系数 Fig. 13 Temporal coefficients of the first two modes and lift coefficient in the same period |
本文采用POD模态分析方法相对于直接对非定常结果进行分析而言，可以更加明确的辨别主导跨声速抖振现象的主要流动相干结构，但是仍然需要进行非定常流场的计算。
3 结 论(1) 在抖振过程中激波运动的相位并不与升力系数的波动相位完全重合，这两者之间有一定的相位差，要明确他们之间的关系需要更进一步的研究。
(2) 在根据OAT15A的非定常计算结果所提取的POD模态中，第一阶模态与第二阶模态的频率与抖振频率相同，是主导抖振现象的主要模态。
| [1] | Mou R K,Yang Y N.Advances of studies for the buffet problem of aircraft[J].Chinese Journal of Applied Mechanics,2001,18:142-150.(in Chinese)牟让科,杨永年.飞机抖振问题研究进展[J].应用力学学报,2001,18(SI):142-150. |
| [2] | Jacquin L,Molton P,Deck S,et al.An experimental study of shock oscillation over a transonic supercritical profile[C]//Toronto:American Institute of Aeronautics and Astronautics,Inc.,2005. |
| [3] | Jacquin L,Molton P,Deck S,et al.Experimental study of shock oscillation over a transonic supercritical profile[J].AIAA Journal,2009,47(9):1985-1994. |
| [4] | Sebastien Deck.Numerical simulation of transonic buffet over a supercritical airfoil[J].AIAA J.,2005,l (43):1156-1566. |
| [5] | Mylene Thiery,Eric Coustols.Numerical prediction of shock induced oscillations over a 2D airfoil:Influence of turbulence modelling and test section walls[J].International Journal of Heat and Fluid Flow,2006,27:661-670. |
| [6] | Sebastian Illi,Thorsten Lutz,Ewald Kramer.On the capability of unsteady RANS to predict transonic buffet[C]//Raunschweig,Germany:Institute of Aerody-namics and Gas Dynamics,2012. |
| [7] | Crouch J D,Garbaruk A,Magidov,et al.Global structure of buffeting flow on transonic airfoils[C]//In IUTAM Symposium on Unsteady Separated Flows and Their Control,Springer:2009. |
| [8] | Crouch J D,Garbaruk A,Magidov,et al.Origin of transonic buffet on aerofoils[J].J.Fluid Mech.,2009,628:357-369. |
| [9] | Xiong Juntao,Li Feng,Luo Shijun.Computation of NACA0012 airfoil transonic buffet phenomenon with unsteady Navier-Stokes equations[C]//Nashville,Tennessee:University of California Irvine,2012. |
| [10] | Xiong Juntao,Liu Feng.Numerical simulation of transonic buffet on swept wing of supercritical airfoils[C]//San Diego:University of California Irvine,2013. |
| [11] | Molton P,Bur R,Lepage A,et al.Control of buffet phenomenon on a transonic swept wing[C]//Applied Aerodynamics Symposium,2012. |
| [12] | Zhang W,Chen C,Sun D J.Numerical simulation of flow around two side-by-side circular cylinders at low Reynolds numbers by a POD-Galerkin spectral method[J].J.of Hydrodinamics,2009,24(1),83-88.(in Chinese)张伟,陈诚,孙德军.低Reynolds数横向排列双圆柱绕流的POD-Galerkin谱方法数值模拟[J].水动力学研究与进展,2009,24(1):83-88. |
| [13] | Wang A X,Ma Y C,Fu Y.Proper orthogonal decomposition for the nonstationary Navier-Stokes equations based on two-grid method[J].Basic Sciences Journal of Textile Universtiles,2009,22(1):76-81.(in Chinese)王阿霞,马逸尘,付英.基于双重网格法的非定常N-S方程POD数值模拟[J].纺织高校基础科学学报,2009,22(1):76-81. |
| [14] | Couplet M,Basdevant C,Sagaut P.Calibrated reduced-order POD-Galerkin system for fluid flow modelling[J].Journal of Computational Physics,2005,207(1):192-220. |
| [15] | Bui-Thanh T,Damodaran M,Willcox K.Aerodynamic data reconstruction and inverse design using proper orthogonal decomposition[J].AIAA Journal,2004,42(8):1501-1516. |
| [16] | Lumley J L.The structure of inhomogeneous turbulence[C]//Moscow:Nauka,1967. |
| [17] | Aubry N,Holmes P,Lumley J L,et al.The dynamics of coherent structures in the wall region of a turbulent boundary layer[J].J.Fluid Mech.,1988,192(1):115-173. |
| [18] | Moehlis J,Smith T R,Holmes P,et al.Models for turbulent plane Couette flow using the proper orthogonal decomposition[J].Phys.Fluids,2002,14(7):2493-2507. |
| [19] | Roe P L.Characteristic based schemes for the euler equations[J].Annual Review of Fluid Mechanics,1986,l (18):337-365. |
| [20] | Jameson A.Time dependent calculations using multi-grid,with applications to unsteady flows past airfoils and wings[R].AIAA-91-1596,1991. |
| [21] | Golias N A,Tsiboukis T D.An approach to refin-ing three dimensional tetrahedral meshes based on delaunay transformations[J].Int.J.Num.Meth.Eng.,1994,l (37):793-812. |
| [22] | Spalart P R,Allmaras S R.A one-equation turbulence model for aerodynamic flows[R].AIAA-92-0439,1992. |