0 引言
风洞试验一般使用缩比模型,风洞模型的缩小以及风洞固有特性的限制,使得风洞试验的Re数与飞机真实飞行Re数存在较大的差异。因此必须对风洞试验数据进行Re数效应修正。
对战斗机的Re数效应研究表明,由于战斗机多采用较薄的翼型,在大气中飞行时,机翼附面层近似于全湍流。Re数对全机的升力特性和纵向力矩特性影响很小,而对表面磨擦阻力有较大的影响。因此,在试验数据修正中,只对阻力做Re数修正,包括最小阻力和升致阻力。
现今民机和高空、高速无人机等,为追求高的巡航效率,一般采用高升阻比翼型,如超临界翼型和超临界层流复合翼型。这些翼型在设计点(巡航状态)均能保持不小于50%弦长的自然层流区。研究表明,在设计状态下层流翼型的阻力比普通紊流翼型的阻力可以减小一倍以上。但当偏离设计点较多时,自然层流区趋于消失。翼型的阻力会迅速增大。同时试验研究也表明,雷诺数通过影响超临界翼型的流场结构和压力分布,进而影响超临界翼型的宏观气动力特性,包括升力、阻力及纵向力矩[1]。雷诺数对超临界翼型流动影响同时反应在转捩位置上。转捩是边界层理论中非常重要的概念,表示由层流流动向湍流流动的转变[2, 3, 4, 5]。
战斗机的Re数效应修正方法是通过变Re数试验,得到最小阻力随Re数变化的线性曲线,采用外插的方法把试验Re数的最小阻力修正到飞行Re数。
本文通过基于γ-Reθ的转捩预测模型对飞机机翼进行数值模拟,得到不同Re数下机翼的自由转捩位置。同时在风洞试验中对飞机机翼进行强制转捩试验,得到机翼不同转捩位置的气动数据。利用CFD计算得到的转捩位置结合强制转捩试验数据,对风洞试验数据的升力、阻力和纵向力矩进行Re数效应修正[6, 7, 8, 9, 10, 11]。
1 计算软件简介本文采用在航空航天行业使用较多的商用CFD软件ANSYS CFX,该软件采用基于有限元的有限体积法,使用全隐式多网格耦合求解,对六面体网格采用24点插值,本文计算模型采用六面体网格,网格数约为1 000万左右。
本文中物体表面设置为无滑移物面边界条件,远场设置为开放边界条件,选取SST湍流模型。转捩模型采用γ-Reθ转捩预测模型,由于该模型得到较为成熟的应用,本文在此不再赘述,见文献[12, 13, 14, 15]。 2 强制转捩试验
为研究机翼不同转捩位置对气动特性的影响,在机翼表面不同位置粘贴金刚砂胶带进行强制转捩风洞试验。根据试验结果显示,最小阻力、零迎角升力、升力线斜率、零升力矩以及纵向安定导数随着转捩位置的变化基本呈线性变化。
M=0.4、0.5、0.6的试验Re数分别1.21×106、1.45×106、1.77×106。从图 1~图 5可以看出,不同马赫数(Re也不同),在相同强制转捩位置,气动特性略有差异。因此在进行Re数效应修正时,首先通过CFD计算得到某马赫数下不同高度的机翼 转捩位置,再根据计算转捩位置,在图 1~图 5中找到相应马赫数和转捩位置的纵向导数值来进行Re数效应修正。
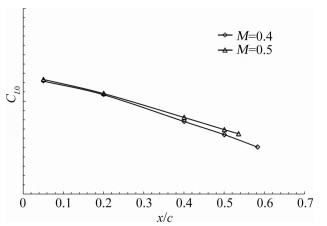 |
| 图 1 零迎角升力系数与转捩位置关系 Fig. 1 The relationship between lift coefficient (α=0) and transition positions |
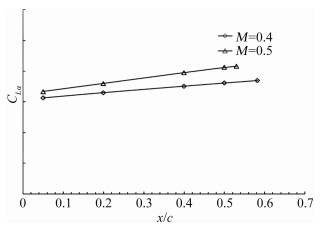 |
| 图 2 升力线斜率与转捩位置关系 Fig. 2 The relationship between lift slope and transition positions |
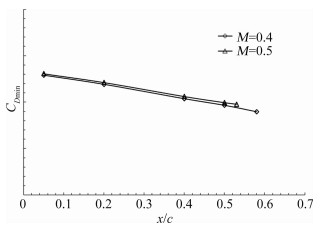 |
| 图 3 最小阻力与转捩位置关系 Fig. 3 The relationship between minimum drag and transition positions |
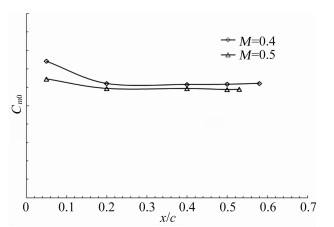 |
| 图 4 零升力矩与转捩位置关系 Fig. 4 The relationship between zero lift pitching moment and transition positions |
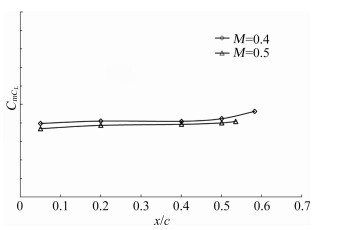 |
| 图 5 纵向力矩导数与转捩位置关系 Fig. 5 The relationship between pitching moment derivative and transition positions |
机翼初期设计考虑到高升阻比以及高临界马赫数的要求,选取了超临界层流复合的翼型。后期由于飞机指标改变,飞行速度降低,没有使用到机翼的超临界特性,因此风洞试验没有完全验证其超临界特性(临界马赫数)。
从图 6可以看出,通过CFD计算可知临界马赫数在0.8(∂CD/∂M=0.18)左右。从图 7和图 8的测压试验和CFD计算对比可以看出,机翼前缘上表面没有较高的负压峰值,上表面中部压力分布也较为平坦,这些都能够有效减弱激波强度,增大临界马赫数。通过试验和CFD仿真分析可以知道机翼的超临界特性良好。
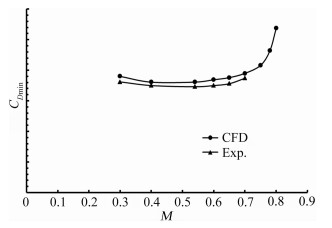 |
| 图 6 机翼最小阻力随马赫数变化曲线 Fig. 6 The curves for minimum drag of wing and Mach number |
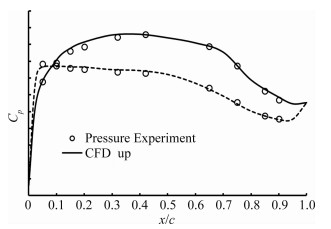 |
| 图 7 M=0.65,α=0°机翼截面压力分布 Fig. 7 The pressure distribution of some wing section (M=0.65,α=0°) |
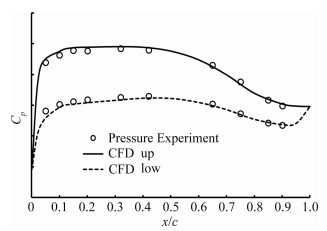 |
| 图 8 M=0.65,α=3°机翼截面压力分布 Fig. 8 The pressure distribution of some wing section (M=0.65,α=3°) |
机翼自由转捩位置较难通过试验直接得到,本文在风洞试验中进行机翼不同位置的强制转捩试验,得到不同转捩位置与纵向导数关系曲线(图 1~图 5),并将自由转捩试验得到的纵向导数在图 1~图 3中进行线性外插,从而得到机翼自由转捩位置。
由于风洞Re数变化范围较小,因此只有Re低于2.5×106的试验数据。计算大气条件与试验相同,从图 9可以看出,机翼计算自由转捩位置较试验靠后约2%当地弦长,计算转捩位置与试验结果随Re变化的趋势相同,计算结果与试验数据基本吻合。
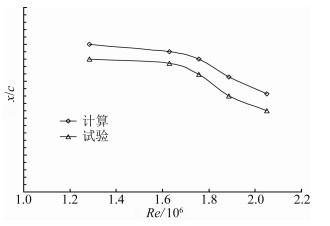 |
| 图 9 试验与计算转捩位置对比 Fig. 9 The transition positions comparing for calculation and experiment |
图 10~图 12为不同Re数的机翼上表面间歇因子云图,从图中可以看出间歇因子在层流段几乎为零,达到转捩位置后间歇因子瞬间增大。从图中可以看出,机翼内段由于受到机身绕流的影响层流段较外翼短,转捩位置沿展向分布也不均匀。
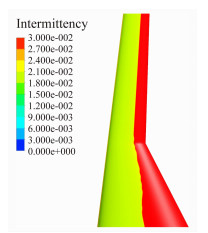 |
| 图 10 Re=2.0×106间歇因子云图 Fig. 10 The intermittent factor contour for Re=2.0×106 |
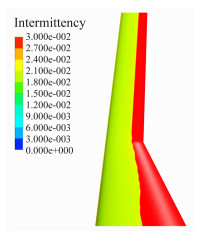 |
| 图 11 Re=5.0×106间歇因子云图 Fig. 11 The intermittent factor contour for Re=5.0×106 |
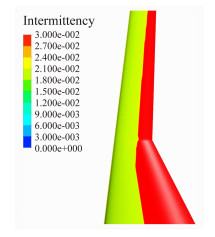 |
| 图 12 Re=8.0×106间歇因子云图 Fig. 12 The intermittent factor contour for Re=8.0×106 |
根据飞机飞行包线,确定飞机的飞行Re数范围,并对该范围的Re数进行数值模拟,计算出不同高度、速度下的转捩位置。由于计算转捩位置较试验有约2%当地弦长的误差,对计算转捩位置进行一定的修正。
Re数效应修正是在试验数据CL、CexpCD、CexpCmexp的基础上,加上Re数修正量ΔCLRe、ΔCDRe、ΔCmRe。而Re数修正量通过如下方法得到:
由CFD计算得到的不同Re数的机翼转捩位置,并根据各纵向导数与转捩位置的线性关系(图 1~图 5),使用计算得到的转捩位置进行线性插值得到对应Re数的纵向导数。用插值纵向导数减去试验值,得到Re数效应修正的纵向导数增量,并通过计算得到Re数修正量ΔCLRe、ΔCDRe、ΔCmRe。
具体修正公式如下 :
CLRe=CLexp+ΔCLRe
ΔCLRe=ΔC强制转捩L0+ΔCLα强制转捩·α
CDRe=CexpD+ΔCDRe
ΔCDRe=ΔCDmin强制转捩
CmRe=Cexpm+ΔCmRe
ΔCmRe=ΔCm0强制转捩+ΔC强制转捩mCL·CLRe
其中ΔCL0强制转捩、ΔCLα强制转捩、ΔCDmin强制转捩、ΔCm0强制转捩和ΔCmCL强制转捩分别为在强制转捩试验曲线上的插值数据与自由转捩试验数据的差值,对非线性段导数ΔCLα强制转捩、ΔCmCL强制转捩进行了相应的修正。不同马赫数和Re数下的计算自由转捩位置如图 13。从图中可以看出,在Re数小于7×106时,转捩位置基本不变,超过该Re数后,转捩位置急剧前移,层流段变短。
风洞试验仅能做到试验模型和速度与飞机真实飞行相似,而无法得到飞机在不同高度下的气动数据。飞机不同的飞行高度反应了飞机Re数的变化。为获取飞机在不同高度下的气动数据,必须对风洞试验数据进行Re数效应修正。
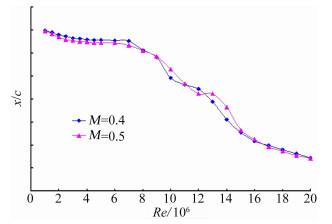 |
| 图 13 CFD计算转捩位置随Re变化曲线(M=0.5) Fig. 13 The curves of CFD transition positions and Re(M=0.5) |
图 14~图 15为不同高度进行Re数修正后的极曲线和俯仰力矩曲线。图 16为经过Re数修正后的风洞试验数据与飞行试验气动数据的对比。飞行试验的升阻力通过飞机飞行过程中的重量以及发动机推力进行反算得到,从图中可以看出,飞行试验数据与风洞试验Re数修正数据基本吻合,试验数据与修正数据的差异是由于发动机推力损失无法准确获取等因素造成。
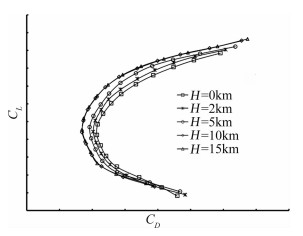 |
| 图 14 进行Re数修正后的升阻极曲线 Fig. 14 The lift-drag polar curves after Reynolds number effect correction |
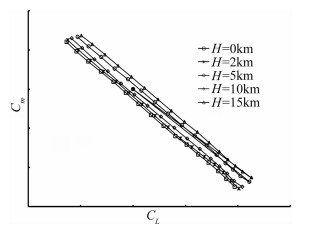 |
| 图 15 进行Re数修正后的力矩曲线 Fig. 15 The pitching moment curves after Reynolds number effect correction |
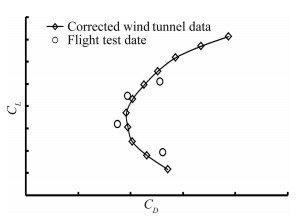 |
| 图 16 Re数修正数据与飞行试验数据升阻极曲线对比 Fig. 16 The comparing for the data after Reynolds number effect correction and flight tests |
通过转捩位置预测结合强制转捩风洞试验的Re数效应修正方法,使得风洞试验数据更加准确、可靠。修正方法已应用于超临界层流复合翼飞机的Re数效应修正中,并得到飞行试验的验证,可为同类飞机的风洞试验数据Re数效应修正提供可靠的修正方法。
| [1] | Xu Xin, Liu Dawei, Chen Dehua, et al. Analysis of llow over supercritical airfoil for Reynolds numbers effects[R]. CSTAM 2012-B03-0140, 2012. (in Chinese) 许新, 刘大伟, 陈德华, 等. 超临界翼型雷诺数影响流动分析[R]. CSTAM 2012-B03-0140, 2012. |
| [2] | Chen Yinchun, Si Jiangtao, Han Xianli, et al. Investigation of transition effect on the pressure distribution of supercritical wing[J]. Acta Aerodynamica Sinica, 2003, 21(4): 470-475. (in Chinese) 陈迎春, 司江涛, 韩先锂, 等. 转捩对超临界机翼压力分布的影响分析[J]. 空气动力学学报, 2003, 21(4): 470-475. |
| [3] | Yang Qingzhen, Zhang Zhongyin. Analysis of the boundary layer and aerodynamic characteristics of a supercritical laminar wing[J]. Acta Aeronautica et Astronautica Sinica, 2004, 25(5): 439-442.(in Chinese) 杨青真, 张仲寅. 超临界层流机翼边界层及气动特性分析[J]. 航空学报, 2004, 25(5): 439-442. |
| [4] | Chen Yi, Gao Zhenghong. Application of gamma-theta transition model to flows around airfoils[J]. Acta Aerodynamica Sinica, 2009, 27(4): 411-418. (in Chinese) 陈奕, 高正红. Gamma-Theta转捩模型在绕翼型流动问题中的应用[J]. 空气动力学学报, 2009, 27(4): 411-418. |
| [5] | David B DeGraff, Donald R Webster, John K Eaton. The effect of Reynolds number on boundary layer turbulence[J]. Experimental Thermal and Fluid Science, 1999, 18: 341-346. |
| [6] | Suzen Y, Huang P. Modeling of flow transition using an intermittency transport equation[J]. Journal of Fluids and Engineering, 2000, 122(2): 273-284. |
| [7] | Suzen Y B, Xiong G, Huang P G. Prediction of transition flows in a low-pressure turbine using an intermittency transport equation[R]. AIAA 2000-2645. |
| [8] | Zhang Yulun, Wang Guangxue, Meng Dehong, et al. Calibration of γ-Reθ transition model[J]. Acta Aerodynamica Sinica, 2011, 29(3): 295-301.(in Chinese) 张玉轮, 王光学, 孟德宏, 等. γ-Reθ转捩模型的标定研究[J]. 空气动力学学报, 2011, 29(3): 295-301. |
| [9] | Langtry R B, Menter F R. Transition modeling for general CFD applications in aeronautics[R]. AIAA 2005-522. |
| [10] | Mayle R E. The role of laminar-turbulent transition in gas turbine engines[J]. ASME Journal of Turbo Machinery, 1991, 113: 509-537. |
| [11] | Langtry R B, Menter F R, Likki S R, et al. A correlation based transition model using local variables: part Ⅱ-test case and industrial application[R]. ASME-GT 2004-53454, ASME Turbo Expo 2004 Vienna Austria, 2004. |
| [12] | Menter F R, Langtry R B, Likki S R, et al. A correlation based transition model using local variables: part I-model formulation[R]. ASME-GT 2004-53452. ASME Turbo Expo 2004 Vienna Austria, 2004. |
| [13] | Langtry R B. A correction-based transition model using local variables for unstructured parallelized CFD codes[D].[PhD Thesis]. Stuttgart, 2006. |
| [14] | Poll D I A. Laminar to turbulent transition[C]//IUTAM SYM. 1979: 253-260. |
| [15] | Erik J, Ponnampalam B. On the stability of three-dimensional boundary layers, Part 1: Linear and non-linear instiblity[R]. I2-CASE Report 99219. 1999. |


