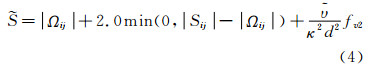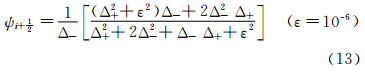0 引 言
旋翼是直升机的关键部件，它提供了直升机飞行所需的升力、推进力及操纵力，而悬停状态作为直升机重要且特有的运动状态，其旋翼流场具有根部为低速流动、尖部为跨声速流动，并会出现强烈集中的螺旋桨尖涡，对旋翼气动特性有重要的影响，因而高效及高精度的模拟悬停状态下旋翼流场的涡尾迹特征及气动特性一直是直升机技术领域的研究热点与难点之一[1]，同时它也为直升机旋翼前飞流场的模拟提供了理论基础。
相比于传统的试验方法和理论方法，基于RANS方程的先进CFD数值模拟方法具有周期较短、成本较低，并且能充分捕捉流场细节尤其是跨声速流场的激波特性、涡的形成及输运特性等优点。随着计算机技术水平不断发展，旋翼CFD方法取得了长足的进步。20世纪80年代，Agarwal等[2]通过求解无粘可压Euler方程得到了悬停状态下的旋翼流场。90年代以后，Srinivasan等[3]首次采用NS方程计算了模型旋翼悬停状态下的流场，计算得到的桨叶表面压强分布与试验值吻合的较好。但由于数值耗散过大，使得桨尖涡的模拟存在着失真现象。Pomin和Wagner等[4]则采用嵌套网格技术和NS方程对ONERA7A旋翼的悬停流场及气动性能进行了数值模拟，取得了良好效果。最近，Duraisamy等[5]发展了一种基于重叠网格和WENO 格式的旋翼悬停粘性流场的数值模拟，计算结果揭示了高阶格式对桨尖涡模拟的有效性。与国外相比，国内学者在旋翼悬停流场的研究中也取得了很大的进展。江雄等[6]在国内较早采用双时间方法和重叠网格技术求解NS方程获得了悬停旋翼的流场特性。招启军等[7]采用嵌套网格技术和高效的贡献单元搜索方法进行了悬停旋翼绕流的数值模拟。杨爱明等[8]则采用多重网格方法对旋翼悬停流场进行了数值模拟。之前这些研究揭示了运用CFD方法模拟旋翼粘性绕流的可能性，但它们大多是以显式方法为主，计算效率往往不高；同时对旋翼粘性绕流的模拟也往往局限于采用简单的代数湍流模型(B-L模型[9])，难以捕捉复杂状态下的流动细节特征，特别是旋翼大拉力状态下的失速特性及涡细节特征的高精度模拟。
鉴于此，为了高效及高精度的模拟旋翼粘性绕流的特征，本文发展了一套耦合嵌套网格技术、S-A湍流模型[10]、LU-SGS隐式算法[11]、OpenMP并行策略的RANS方程求解方法，其中对流通量采用高阶Roe-MUSCL格式[12]进行离散，特别的对于附加的 涡运动粘性系数方程，本文着重考虑了方程源项对隐式离散方程的贡献并进行推导。通过对不同旋翼翼型和悬停状态C-T以及UH-60A旋翼粘性绕流的数值模拟，结果表明了该方法相较于传统显式推进方法能显著地提高计算效率，同时相比于代数湍流模型，耦合S-A模型的RANS方程求解方法能更好的模拟旋翼翼型、旋翼三维流场细节特征及气动特性。
1 旋翼嵌套网格系统 1.1 旋翼C-O型网格生成方法旋翼翼型网格是旋翼网格生成的基础，考虑粘性对流场的影响，本文采用求解Poisson方程的网格生成方法生成旋翼翼型剖面网格，并通过Higenstock[13]源项修正策略调整网格的疏密及正交程度。为了能准确的模拟附面层粘性流动，第一层翼型网格的壁面距离为5×10-6c(y+≈1)，其中c为翼型弦长。
在剖面翼型网格的基础上，对于桨叶段网格通过桨叶展向剖面间插值生成，而对于桨根、桨尖处考虑到C-H型网格易出现大变形、非光滑过渡等问题，则采用绕翼型中弧线翻折策略生成桨叶的C-O型结构网格。为了避免桨叶网格在嵌套时超出背景区域边界，靠近桨根位置应采取相关塌缩措施。图 1则给出了针对UH-60A后掠桨叶网格的插值和翻折过程示意图。
 |
| 图 1 UH-60A桨叶网格插值、翻折过程示意图 Fig. 1 Schematic of the interpolation and folding process of UH-60A blade grid generation |
本文采用嵌套网格方法对旋翼悬停流场进行数值模拟，其中嵌套网格系统由围绕旋翼桨叶的C-O型贴体结构网格和圆柱背景网格两部分组成。考虑悬停流场具有轴对称性质，采用周期性边界条件，只需取1/N(N为桨叶片数)全场。为了解决嵌套网格技术中的相关难点，采用高效鲁棒的“扰动衍射”方法(DDM)快速确定桨叶在背景网格中的洞边界，同时结合Inverse Map方法对背景网格洞单元的贡献单元进行快速搜寻。当采用DDM方法时，选取围绕桨叶的包络面因尽量避免靠近桨叶表面的非线性流动区域，从而保证三线性插值的精度。图 2和3分别给出了针对UH-60A悬停旋翼的嵌套网格和背景网格洞边界单元图。
 |
| 图 2 UH-60A桨叶嵌套网格图 Fig. 2 Embedded grid system of UH-60A blade |
 |
| 图 3 UH-60A桨叶背景网格洞边界单元图 Fig. 3 Hole boundary cells in the background grid of UH-60A blade |
对于悬停旋翼，定义坐标轴固连于旋转桨叶上，采用准定常流动方法计算桨叶的流场，将守恒积分形式的可压RANS方程与Spalart-Allmaras湍流模型进行耦合，可得到如下的控制方程：
其中，守恒变量 W =[ρρuρvρwρEv]T。此外，V为控制体体积，V为控制体表面积，n =[nxnynz]T为控制体表面的法矢量。
对于无粘通量、粘性通量、旋转通量，其表达式分别为：
式中ρ、 U (u,v,w)、p、E、ν、v、k、τ和 ω 分别表示气体密度、绝对速度、压强、总内能、层流运动粘性系数、涡运动粘性系数、热传导系数、粘性应力张量和旋转角速度矢量； r 为控制体单元体心到旋转轴的位置矢量。式(2)中v涡运动粘性系数方程的源项分量Tsa的表达式为：
对于旋转流动,为了更好的限制S-A湍流模型可能引起的粘性过大的问题，本文在标准模型的基础上采用了文献[14]提出的对生成源项
的修正公式：
为了提高流场求解的效率，本文的时间推进方法采用隐式LU-SGS格式。此外，采用隐式格式也可以克服模型方程的刚性，提高计算的稳定性。对时间导数进行离散后得：
其中，ψ n= W n+1－ W n，代入上式，利用 其中，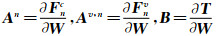
分别为对流项、扩散项和源项的Jacobian矩阵(系数)，则可得到关于 ψ n的方程：
对于悬停流场，由于计算的RANS方程耦合了涡运动粘性系数v的输运方程，特别需要考虑该方程的源项。忽略源项Tsa中高阶项对偏导数的影响，则可得
式(8)采用LU-SGS格式推进求解，则 其中LU分解矩阵 L、D、U 的表达式分别为 其中，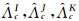
和
分别为流场在I、J、K方向上的无粘谱半径和粘性谱半径。系数α为大于1的稳定性常数，α取值越大，格式的稳定性越好，但会降低收敛速度，在本文计算中取为1.01。系数β对于 方程取为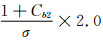
，对于其它方程取为2.0。
3.2 空间离散
对于控制方程，空间离散采用有限体积法，对于交界面上的对流通量，采用ROE格式计算无粘通量：
其中，原始变量为 q = [ρuvwpv]T，
为Roe平均算子，下标i+1/2表示单元交接面，L、R分别表示单元交接面的左右两侧。
网格面上的流动变量采用三阶MUSCL格式插值获得：
上式中，Δ－、Δ+分别为后差、前差算子。参数κ取为κ=1/3。为了避免在非线性流动区域插值引起的数值振荡，同时引入Venkatakrishnan限制器：
对于粘性通量采用二阶中心格式进行计算。
3.3 初始条件与边界条件1) 初始条件
流场守恒变量的初始值由来流给定，其初值为：
其中，Re为雷诺数。
2) 边界条件
在物面，速度满足无滑移边界条件，涡运动粘性系数 在物面取值为0，且满足相应的热力学与动力学条件即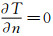
和
。对于远场，流场的守恒变量可采用一维Riemann不变量(R+,R－)来进行处理。特别的由于悬停流场具有旋转对称性，因此只需计算一片桨叶，而其余桨叶以及自身尾迹的影响通过周期性边界条件来实现。
为了进一步提高流场计算效率，本文引入基于数据共享存储体系结构的OpenMP并行计算方法[15]。采用该方法时，只需在原有串行程序基础上对每个计算循环采取互不相关单元分区同时求解，从而加速流场求解。
对于下文算例3，其桨叶网格大小为225×49×57，背景网格大小为91×138×117。计算基于四核CPU配置(单核主频3.4GHz)的计算机，采用串行计算需耗时3.9h，而采用并行计算只需耗时1.37h，加速效率达到了65%，可以看出明显加速了流场的求解。
4 算例计算与分析 4.1 二维旋翼翼型数值模拟为了验证本文发展的耦合S-A模型的RANS方程隐式求解算法在旋翼翼型绕流的求解精度及计算效率，选择了以下2个算例。其计算条件如表 1所示，其中：Ma为马赫数，α为迎角。
| Case | α | Ma | Re | |
| C1 | RAE 2822 | 2.79° | 0.73 | 6.5×106 |
| C2 | NACA 0012 | / | / | 3.0×106 |
对于跨声速粘性绕流，算例采用C型结构网格来计算翼型流场，网格大小为369×65，其中在翼型表面布置了302个网格单元；为了能较好的捕捉附面层内流场细节，第一层网格的壁面距离取为5×10-6c(y+≈1)，远场边界取大约20倍的弦长。
图 4给出了该状态下基于耦合S-A湍流模型隐式LU-SGS方法计算和显式Runge-Kutta方法计算的密度残值收敛时间曲线对比。当采用隐式算法时，密度残值收敛4.5个量级时需要的迭代步数约为显式的1/4左右，而总的计算时间则约为显式的3/10左右。表明该方法既增加了方程的收敛稳定性，又提高了计算效率。
 |
| 图 4 C1状态显/隐式密度残值随时间收敛曲线对比 Fig. 4 Comparisons of time convergence history of density residual for explicit and implicit scheme at state C1 |
图 5给出了RAE2822翼型基于耦合S-A湍流模型隐式求解的翼型表面压强系数分布与试验值[16]的对比。作为比较，同时也计算了基于B-L湍流模型的压强系数分布。从图 5可知，基于耦合S-A湍流模型的压强系数分布相比于B-L模型的计算结果更加贴近于试验值，且能更好地捕捉翼型上表面的绕流与激波位置。
表 2则分别给出了该状态下基于耦合S-A和B-L湍流模型计算的气动力系数与试验值的对比。从表 2可知，与B-L模型相比，基于S-A湍流模型计算的翼型阻力系数CD和力矩系数Cm与试验值更加贴近些，对于翼型升力系数CL两者相差不大。
 |
| 图 5 C1状态翼型表面压强系数对比 Fig. 5 Comparisons of calculated pressure coefficient distributions with experimental data at state C1 |
| Method | CL | CD | Cm |
| B-L model | 0.788 | 0.0148 | -0.090 |
| S-A model | 0.783 | 0.0157 | -0.092 |
| Experimental data | 0.803 | 0.0168 | -0.099 |
在模拟翼型跨声速粘性绕流的基础上，算例2则对NACA 0012翼型在不同迎角下的升力及阻力系数曲线进行了数值模拟。图 6和7分别给出了基于耦合S-A或B-L湍流模型隐式求解的翼型升力和阻力系数随迎角的变化曲线与试验值[17]的对比。由图 6可知，基于耦合S-A湍流模型的计算要比采用B-L湍流模型能更好的模拟翼型升力系数的静态失速特性；对于翼型阻力系数的模拟，图 7表明采用耦合S-A模型的计算结果更贴近试验值。图 8则对比了采用耦合S-A模型与B-L模型计算的翼型在18°迎角下的流线图，可以看出采用S-A湍流模型能很好的捕捉旋翼翼型失速的分离特征，而此时采用B-L模型却捕捉不到，这与图 6的结果是相对应的。
 |
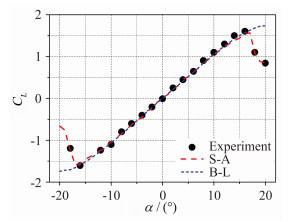| 图 6 C2状态下翼型升力系数曲线对比 Fig. 6 Comparisons of airfoil lift coefficient curve at state C2 |
 |
| 图 7 C2状态下翼型阻力系数曲线对比 Fig. 7 Comparisons of airfoil drag coefficient curve at state C2 |
 |
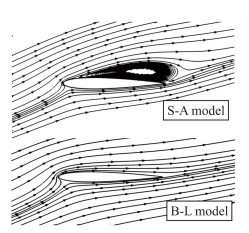| 图 8 C2状态18°迎角下不同模型计算的翼型流线图 Fig. 8 Comparisons of calculated streamline of airfoil at 18 degree AOA and state C2 by different models |
在旋翼翼型数值分析的基础上，进一步验证本文发展的耦合S-A湍流模型的RANS方程隐式求解算法在三维旋翼悬停流场的计算精度及效率。本文采用嵌套网格方法分别对“Caradonna-Tung”(C-T)模型旋翼和UH-60A 旋翼的气动特性进行了数值模拟，计算状态如表 3所示，其中：Matip代表桨尖马赫数，θ代表总距角，Re代表雷诺数。
| Case | Rotor | Matip | θ | Re |
| C3 | C-T | 0.610 | 12° | 2.68×106 |
| C4 | C-T | 0.877 | 8° | 3.93×106 |
| C5 | UH-60A | 0.628 | 9° | 2.75×106 |
悬停C-T模型旋翼含有两片桨叶，桨叶外形为矩形，桨叶半径为1.143m，桨叶的展弦比为6。对于该旋翼，桨叶剖面翼型为NACA0012翼型，无负扭转。算例的桨叶网格大小为225×49×57，第一层桨叶网格的壁面距离为5×10-6c(y+≈1)。对于背景网格，其网格大小为81×125×89。
图 9给出了C3状态下采用耦合S-A湍流模型和隐式LU-SGS算法计算与显式Runge-Kutta算法计算的密度残值时间收敛曲线对比。当采用隐式算法密度残值收敛到目标标准只需迭代2 579步，而显式则需迭代10 158步，且隐式的计算时间约为显式的1/3左右，从而有效地提高了悬停流场的计算效率。图 10则给出了隐式算法求解的旋翼拉力系数(CT)及悬停效率(Figure of Merit,FM)的残值收敛曲线，可见当密度残值收敛到目标量级时，旋翼拉力系数与悬停效率也达到较好的收敛。
 |
| 图 9 C3状态旋翼桨叶密度残值随时间收敛曲线对比 Fig. 9 Comparisons of time convergence history of density residual of blade for explicit and implicit scheme at state C3 |
 |
| 图 10 C3状态旋翼拉力系数与悬停效率收敛曲线 Fig. 10 Comparisons of convergence history of rotor thrust coefficient and FM at state C3 |
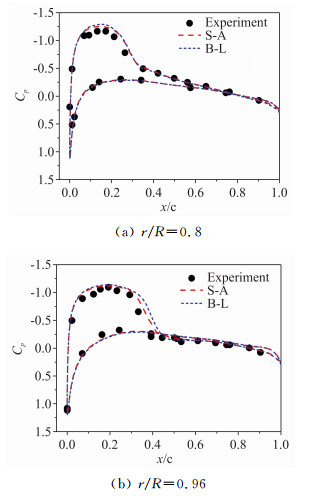
图 11则给出了基于耦合S-A湍流模型的RANS方程隐式计算的桨叶不同剖面的压强系数分布的计算结果与试验值[18]的对比，同时图中也给出了采用B-L湍流模型的计算结果。相比于B-L湍流模型，耦合S-A湍流模型模拟的计算结果更接近于试验值，特别的对于桨尖位置处负压峰值的模拟具有相对更高的计算精度。
 |
| 图 11 C3状态旋翼桨叶不同剖面压强系数分布对比 Fig. 11 Pressure coefficient distributions on the rotor blade at state C3 |
为了能更好的捕捉旋翼的桨尖涡流动，以粗网格计算得到的涡心轨迹位置为参考，在粗网格的基础上在桨叶展向0.7R~1.05R以及桨叶下方位置0~ 0.6R内的区域内进行了适当的网格加密，加密后的细 网格数目为91×138×117。图 12和13则给出了采用不同大小背景网格计算获得的涡量等值面图，以及涡龄角90度截面上的无量纲等涡量线图，可以看到对于粗网格在90°截面上仅能捕捉到三个集中桨尖 涡，而细网格则能捕捉到四个集中桨尖涡。图中由上往下的桨尖涡的涡龄角相差180°，且随着涡龄角的增大，漩涡的强度逐渐减弱。这表明根据涡心轨迹位置适当加密背景网格能有效提高对悬停状态涡尾迹的捕捉精度。
 |
| 图 12 C3状态采用粗网格与细网格计算的涡量等值面对比 Fig. 12 Comparisons of calculated vorticity iso-surface based on the coarse and fine grid at state C3 |
 |
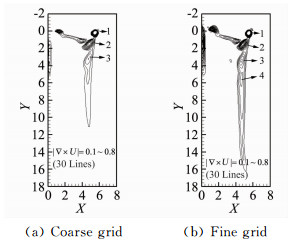| 图 13 C3状态采用粗网格和细网格计算的90°涡龄角截面上的无量纲等涡量线 Fig. 13 Comparisons of dimensionless vorticity line based on the coarse and fine grid at 90 wake age at state C3 |
图 14分别给出了C4跨声速状态下的桨叶不同剖面压强系数分布的计算结果与试验值[18]的对比，并同时对比了S-A和B-L湍流模型的计算结果。相比于B-L湍流模型，耦合S-A湍流模型求解能更好的模拟旋翼在有激波状态下的跨声速流场特征，特别是激波位置捕捉更精确。图 15则给出了采用耦合S-A模型计算的桨叶表面流线图以及压强分布图，由图可见在当前状态下近桨尖位置桨叶上表面有激波出现，而对应的区域也发生了激波诱导的分离以及分离后的再附现象。图 16则给出了采用本文方法计算细网格得到的旋翼桨尖涡涡核的轴向位置与径向位置。对比试验数据，表明该方法能精确的捕捉桨尖涡的空间位置。图 17给出了模拟得到的C4状态90°涡龄角下的旋翼涡量图，图中清晰的反映了悬停状态旋翼尾迹的收缩特性及桨尖涡强度随高度不断衰减的特征，符合实际物理规律。
 |
| 图 14 C4状态旋翼桨叶不同剖面压强系数分布对比 Fig. 14 Pressure coefficient distributions on the rotor blade at state C4 |
 |
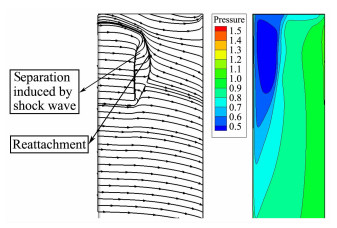| 图 15 C4状态桨叶表面流线与压强分布 Fig. 15 Streamline and pressure contour of blade at state C4 |
 |
| 图 16 C4状态桨尖涡涡核位置的计算值与试验值对比 Fig. 16 Comparisons of the calculated position of blade-tip vortex core with experimental data at state C4 |
 |
| 图 17 C4状态90度涡龄角下的旋翼尾迹涡量图 Fig. 17 Vorticity contour of rotor wake at 90 wake age and state C4 |
从C3和C4算例表明本文建立的基于耦合S-A湍流模型的RANS方程隐式求解方法能高效且较好的模拟常规外形旋翼悬停流场的气动特性以及流场细节特征。
4.2.2 UH-60A旋翼UH-60A旋翼采用了先进桨叶气动外形布局，它由四片桨叶组成，每片桨叶半径为8.18m，该桨叶的展弦比为15.51。桨叶翼型的配置方式分为三段，它的两端采用SC1095翼型，中段采用SC1094R8翼型；且桨叶具有非线性负扭转分布以及20°后掠桨尖，其具体参数见文献[19]。
图 18分别给出了UH-60A旋翼在C5状态下桨叶不同剖面压强系数分布的计算结果与试验值[19]的对比，其中图中同时给出了S-A和B-L湍流模型的计算结果。相比于B-L湍流模型，采用S-A湍流模型的流场计算精度更高，特别是能更好的模拟桨尖后掠位置处的压强分布。图 19还给出了该状态下桨叶展向的拉力系数分布，可知耦合S-A模型求解与试验值吻合的更好，特别是对于桨尖位置处的剖面拉力系数的模拟。
 |
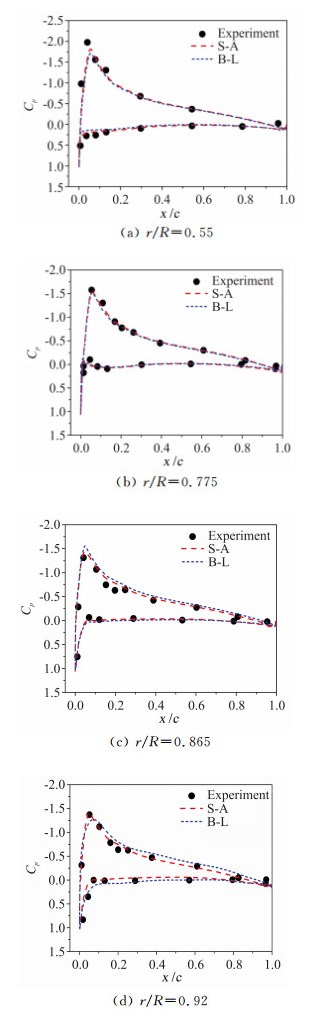| 图 18 C5状态旋翼桨叶不同剖面压强系数分布 Fig. 18 Pressure coefficient distributions on the rotor blade at state C5 |
 |
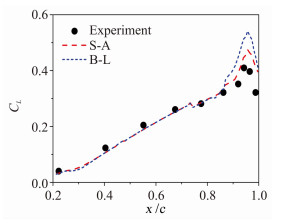| 图 19 C5状态旋翼桨叶不同剖面拉力系数分布曲线 Fig. 19 Prediction of the blade spanwise lift coefficient distribution at state C5 |
图 20给出了该状态不同总距角下采用耦合S-A模型或B-L模型计算的旋翼悬停效率随拉力系数的变化趋势，耦合S-A模型的计算结果在整个试验范围内与试验值能更好的吻合。这表明本文方法不仅可以准确模拟常规气动外形桨叶，也可以有效地对具有先进气动外形的桨叶进行流场及气动特性的数值模拟。
 |
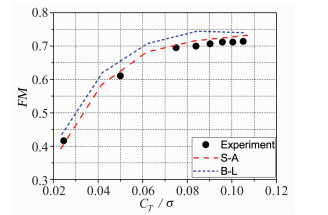| 图 20 UH-60A旋翼悬停效率与拉力系数曲线 Fig. 20 Thrust coefficient and FM curve of UH-60A rotor |
为了提高旋翼粘性绕流的模拟精度和效率，本文发展了一套耦合嵌套网格技术、S-A湍流模型、LU-SGS隐式算法、OpenMP并行策略的RANS方程求解方法，用于求解不同旋翼翼型和悬停旋翼可压粘性绕流，通过算例计算和分析，得到如下结论：
(1) 相比于基于B-L湍流模型的RANS方程求解，耦合S-A湍流模型的求解方法能更好的模拟旋翼翼型及三维旋翼悬停的流场与气动特性，特别能更好的模拟先进气动外形旋翼桨尖位置处的流动细节以及扭矩(阻力)。
(2) 相比于传统显式Runge-Kutta算法推进，采用LU-SGS隐式时间推进和基于数据共享的OpenMP并行策略都可以有效地提高计算效率。
(3) 根据涡核位置适当加密背景网格区域，能更好的捕捉悬停状态旋翼桨尖涡的细节特征。
| [1] | Leishman J G. Rotorcraft aeromechanics:getting through the dip[J]. Journal of the American Helicopter Society, 2010, 55(1):1-24. |
| [2] | Agarwal R K, Deese J E. Euler calculations for flowfield of a helicopter rotor in hover[J]. Journal of Aircraft, 1987, 24(4):231-238. |
| [3] | Srinivasan G R, Baeder J D, Obayashi S, et al. Flowfield of a lifting rotor in hover-A Navier-Stokes simulation[J]. AIAA Journal, 1992, 30(10):2371-2378. |
| [4] | Pomin H, Wagner S. Navier-Stokes analysis of helicopter rotor aerodynamics in hover and forward flight[J]. Journal of aircraft, 2002, 39(5):813-821. |
| [5] | Duraisamy K, Baeder J D. High resolution wake capturing methodology for hovering rotors[J]. Journal of the American Helicopter Society, 2007, 52(2):110-122. |
| [6] | Jiang Xiong, Chen Zuobin, Zhang Yulun. Numerical simulation of a hovering rotor flowfield using a dual time method[J]. ACTA Aerodynamica Sinica,1998, 16(3):288-296. 江雄,陈作斌,张玉伦.用双时间法数值模拟悬停旋翼流场[J].空气动力学学报, 1998, 16(3):288-296. |
| [7] | Zhao Qijun, Xu Guohua, Zhao Jingen. Numerical simulations of the unsteady flowfield of helicopter rotors on moving embedded grids[J]. Aerospace science and technology, 2005, 9(2):117-124. |
| [8] | Yang Aiming, Yang Xiaoquan. Multigrid acceleration and chimera technique for viscous flow past a hovering rotor[J]. Journal of aircraft, 2011, 48(2):713-715. |
| [9] | Lomax H, Baldwin B S. Thin layer approximation and algebraic model for separated turbulent flows[R]. AIAA-78-257, 1978. |
| [10] | Spalartp R, Allmaras S R. A one-equation turbulence model for aerodynamic flows[R]. AIAA-92-0439, 1992. |
| [11] | Yoon S, Jameson A. An Multigrid LU-SSOR Scheme for Approximate Newton Iteration Applied to the Euler Equations[M]. National Aeronautics and Space Administration, 1986. |
| [12] | Roe P L. Approximate Riemann solvers, parameter vectors, and difference schemes[J]. Journal of Computational Physics, 1981, 43(2):357-372. |
| [13] | Hilgenstock. A fast method for the elliptic generation of three-dimensional grids with full boundary control[C]//Proceedings of the Second International Conference, 1988:137-146. |
| [14] | Dacles-Mariani J, Zilliac G G, Chow J S, et al. Numerical/experimental study of a wingtip vortex in the near field[J]. AIAA Journal, 1995, 33(9):1561-1568. |
| [15] | Chandra R. Parallel Programming in OpenMP[M]. Morgan Kaufmann, 2001. |
| [16] | Holst T L. Viscous transonic airfoil workshop compendium of results[J]. Journal of Aircraft, 1988, 25(12):1073-1087. |
| [17] | Abbott I H, Von Doenhoff A E. Theory of Wing sections:Including a Summary of Airfoil Data[M]. Courier Corporation, 2012. |
| [18] | Caradonna F X, Tung C. Experimental and analytical studies of a model helicopter rotor in hover[J]. Vertica, 1981, 5(2):149-161. |
| [19] | Abhishek A, Datta A, Chopra I. Prediction of UH-60A structural loads using multibody analysis and swashplate dynamics[J]. Journal of Aircraft, 2009, 46(2):474-490. |