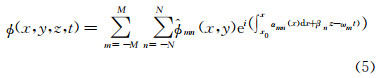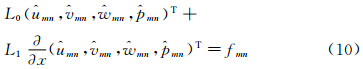0 引言
不可压缩边界层转捩的实验研究发现当二维扰动的幅值增长到一定阶段时,在下游会观察到三维扰动的产生,并且三维扰动的增长率要远大于其线性理论预测的增长率。1962年Klebanoff[1]等人对平板边界层的非线性扰动演化及转捩问题进行了系统研究,发现了其流向的Λ涡结构如图 1(a)所示的K型三维扰动。Saric[2]等人在1984年用烟线实验研究了转捩中快速增长的三维扰动,在下游观察到如图 1(b)所示的交错的Λ涡结构，即C型和H型扰动。
 |
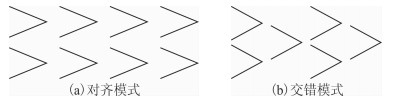| 图 1 烟线演化示意图 Fig. 1 The smoke line evolution |
Kachanov和Levchenko[3]通过实验研究发现在不可压缩平板边界层中，如果加入的二维波的初始幅值很小，就会出现C型转捩，当幅值稍微增大时，将会出现H型转捩，当幅值更大时，就会出现K型转 捩。在Kachanov实验的基础上Corke和Mangano[4] 用热线感应的实验方法对扰动的初始幅值更小的C型和H型转捩问题，并考虑了二维与三维扰动的相位角，结果发现，增大二维扰动的初始幅值会使转捩提前发生，并且不同的相位角会影响三维扰动的增长速度。Zelman[5]和Sayadi[6]等用数值模拟的方法对Kachanov实验进行分析，得到了与实验数据定性上相符的结果。在Kachanov实验的启发下，董亚妮和周恒[7]用直接数值模拟的方法验证了可压缩流体中二次失稳和三波共振机制的存在。三波共振的理论研究方面，Herbert[8, 9]用二次失稳理论，对三波共振中参数共振阶段做了详细的解释。Mankbadi[10]等考虑了临界层中扰动的非线性作用这一方面来对参数共振阶段进行了分析，并说明二维平面波在参数共振阶段一直遵循着线性指数增长。Mankbadi,Wu & Lee[11]和Wu[12]用三层结构理论研究了Blasius边界层中上支界扰动的三波共振情况，他们发现非线性作用主要发生在临界层以及附近的‘扩散层’中，临界层处的非线性作用以及粘性决定着扰动的发展。
本文将研究三波共振中三维扰动在边界层中的非线性作用情况，观察了三维扰动及由于非线性作用产生的其他高次谐波的扰动演化情况，并与实验结果进行了对比。我们采用了一种比较方便的PSE方法来研究上述问题，该方法相对于eN方法需要较多的计算，但是相比与直接数值模拟方法(DNS)节省很多的计算量，同时还可以考虑流动的非平行性，解决扰动的非线性演化过程，与现实中扰动的演化情况相比是比较符合的。并且我们采用了一种新的求解流向波数α的方法，不用再对α进行迭代求解，节省了计算时间和计算量。因此本文用改进后的PSE方法来研究边界层中扰动的演化过程，分析三维扰动在Blasius边界层中的非线性作用。
1 控制方程和数值方法我们用来流速度U∞*作为特征速度，流体的密度ρ0*作为特征密度，计算入口处的边界层排移厚度δ0*作为特征长度，用ρU*2∞作为压力的特征尺度，用
作为时间的特征尺度，其中δ0*=1.7208
,ν*=μ*/ρ*是运动粘性系数。把瞬时速度和压力分解成基本流和扰动两部分之和，把瞬时量带入无量纲的N-S方程中，并减去基本流。便得到在直角坐标系下，不可压缩流体中扰动的表达形式为：
假设扰动是时间和展向的周期函数，扰动表示为：
式中，
(x,y)为形状函数，αmn为流向波数，其频率为ωm=mω0，展向波数为βn=nβ0，ω0、β0为基本频率和基本展向波数，同样形状函数(x,y)和波数αmn(x)都是x的缓变函数。将扰动表达式带入到非线性扰动方程中，并忽略掉流向的二阶导数以及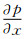
项，便得直角坐标系下的非线性抛物化方程(PSE)，具体推导参见文献[13]：
式中：
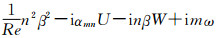
将PSE方程写成算子的形式：
式中fmn表示非线性项。
求解PSE方程最关键的是如何确定流向波数α，通长采用的方法是选取下列四个补充条件的其中之一：
式中上标c表示复共轭，这些条件都是以基本扰动的形状沿流向不变，或者动能沿流向不变为前提的。对于线性PSE，在扰动幅值比较小并且边界层沿流向的变化不太快时，上述前提条件是可以满足的。但是在非线性PSE中，如果扰动的幅值比较大，非线性作用开始体现出来时，基本扰动会有较大的变形；另一方面，在边界层沿流向变化比较快时，即使是线性PSE，基本扰动的变形也会比较快，所以上述补充条件的前提就不成立了。除此之外，使用以上补充条件时，需要对基本波数α进行迭代求解，计算时间很长并且计算量比较大。
依据流动稳定性理论，我们建议了一种新的求解流向波数α的补充条件，即对某个流向位置利用：
来确定当地位置处的流向波数αmn，再由非线性抛物化稳定性方程计算扰动向下游的演化。我们这样处理的原因是，线性算子L0反应了当地平行流假设下扰动波特性，而当地基本波数αmn应该满足当地平行流假设下扰动波的特性，因此由L0来确定αmn。
本文采用的基本流是二维平板Blasius相似性解入口条件。流向x方向上采用Karniadakis等[14]建议的显隐结合的三阶计算格式进行离散，法向y方向我们采用Malik[15]差分格式，有四阶精度并且可以适用于变间距网格。流向方向网格选取等间距网格，为了保证壁面边界层内的网格点数足够多，法向y方向上选取变间距网格。
2 数值结果首先针对Kachanov和Levchenko[3]的实验，参考其扰 动参数(x*=600 mm，雷诺数Reδ1*=U∞*·δ*1/ν*=1 046，边界层排移厚度
=1.7 mm，来流U∞*=9.18 m/s)，选取计算域入口的扰动为一个二维波和一对三维波。
| 频率ω | αr | αi | β | |
| 2D | 0.1297 | 0.35536 | -0.00525 | |
| 3D | 0.06485 | 0.15637 | 0.00900 | ±0.35 |
依据实验中测量的扰动演化曲线，我们提取了二维扰动的初始幅值A2D,rms=5×10-3、三维波初始幅值A3D,rms=3×10-5，并用PSE方法计算了的扰动演化情况，同时与实验结果进行了对比。实验中法向测量点固定在y*/δ*=0.26位置处，其中δ*是当地边界层名义厚度。
图 2中，线条是数值结果，符号是实验结果。二维波幅值在初始阶段按照线性指数增长，当穿出中性曲线的中性点(αi=0)时，幅值开始衰减；由于初始阶段几乎没有非线性作用，三维波的幅值会经历一段线性演化，随后由于二维波幅值的增长，二维、三维波之间的三波共振使得三维波快速增长，但二维波在相当一段距离内仍保持自身的线性增长，因此它起着“催化剂”作用；在最后阶段，二维波受到三维波的反作用幅值会再次增长起来。我们可以看出二维波幅值PSE与实验结果相比很符合。由于三维波的初始幅值很小，实验中初始阶段的三维波演化情况很难测出，所以这一阶段的三维波幅值演化可以忽略掉。同时还可以观察到下游三维波幅值的增长情况与实验结果还是比较符合的。
 |
| 图 2 幅值演化曲线比较 Fig. 2 Compared of the amplitude evolution curve |
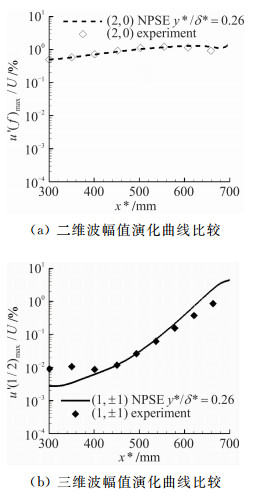
图 3显示的是x*=600 mm处归一化之后的扰动的特征形状函数随法向位置的分布，并与实验数据进行了比较。归一化之后的二维波和三维波特征形状函数分布与实验相比，符合的比较好。同时也说明了实验中测量的扰动是T-S波。
 |
| 图 3 特征形状函数比较 Fig. 3 Compared of the characteristic function |
由于非线性的作用，在扰动演化过程中会产生其他频率的波，我们观察了几种比较特殊的扰动的幅值演化情况，并与实验结果进行了对比，如图 4所示。
 |
| 图 4 高阶扰动幅值演化曲线比较 Fig. 4 Compared of high-order disturbance evolution curve |
在流向比较靠前的位置处就会出现(4,0)波和(3,±1)波，并且其幅值随着流向会快速的增长起来，其结果与实验结果比较相符。(5,±1)在流向比较靠下游的地方出现，幅值增长比较小，与实验结果比较趋势相同，数值上有所偏差。由于(6,0)的幅值很小，实验中测量时有一定的困难，因此，PSE结果与实验结果近似平行，数值上有一定的差距。因为受到实验环境、实验技术、实验条件的影响，实验数据或多或少与数值模拟结果有所不同，但总体定性上、定量上还是比较符合的。
图 5给出了高次谐波归一化之后的特征形状函数分布情况，并将其与实验中的数据进行了比较。其中菱形符号表示实验结果，实线是PSE数值结果。x*=600 mm位置处扰动已经快速的增长起来，此时的非线性作用已经很明显，扰动的特征形状函数会有所变形。考虑到(3,±1)波和(5,±1)波的幅值都比较小，测量中会存在一定的困难，PSE计算结果与实验结果相比较，还是比较符合的。
 |
| 图 5 高阶扰动特征形状函数比较 Fig. 5 Compared of the high-order disturbance characteristic function |
文章用PSE方法研究了三波共振中扰动的演化情况，研究表明实验和PSE数值结果在定量上还是比较相符的。定性上的比较中，二维波在初始阶段和参数共振阶段按照线性指数增长，三维波在初始阶段同样按照线性指数增长。在非线性作用比较强时，三维波快速增长起来，并给二维波一个反作用使得二维波再次增长起来，这与理论描述的结果是一致的。从而证实了三维扰动的非线性作用机制。
| [1] | Klebanoff P S, Tidstrom K D, Sargent L M. The three-dimensional nature of boundary-layer instability[J]. J. Fluid Mech., 1962, 12:1-34. |
| [2] | Saric W S, Thomas A S W. Experiments on the subharmonic route to turbulence in boundary layers[J]. Turbulence and Chaotic Phenomena in Fluids, 1984:117-122. |
| [3] | Kachanov, Yu S, Levchenko V Ya. The resonant interaction of disturbances at laminar-turbulent transition in a boundary layer[J]. J. Fluid Mech., 1984, 138:209-247. |
| [4] | Corke T C, Mangano R A. Resonant growth of three-dimensional modes in transitioning Blasius boundary layers[J]. J. Fluid Mech., 1989, 209:93-150. |
| [5] | Zelman M B, Maslennikova I I. Tollmien-Schlichting-wave resonant mechanism for subharmonic-type transition[J]. J. Fluid Mech., 1993, 252:449-478. |
| [6] | Sayadi T, Hamman C W, Moin P. Direct numerical simulation of complete H-type and K-type transitions with implications for the dynamics of turbulent boundary layers[J]. J. Fluid Mech., 2013, 724:480-509. |
| [7] | DongYani. A numerical study for the resonant triad interaction and secondary instability in a three-dimensional supersonic boundary layer[D].[Master's Thesis]. Tianjin:Tianjin University, 2005. (in Chinese)董亚妮.三维超音速边界层中三波共振和二次失稳机制的数值模拟研究[D].[硕士学位论文].天津:天津大学, 2005. |
| [8] | Herbert T. Subharmonic three-dimensional disturbances in unstable plane shear flows[R]. AIAA-83-1759, 1983. |
| [9] | Herbert T. Secondary instability of boundary layers[J]. Ann. Rev. Fluid Mech., 1988, 20:487-526. |
| [10] | Mankbadi R R. Critical-layer nonlinearity in the resonance growth of three-dimensional waves in boundary layer[R]. 1990, NASA TM-103639. |
| [11] | Mankbadi R R, Wu X, Lee S S. A critical-layer analysis of the resonant-triad in boundary-layer transition:nonlinear interactions[J]. J. Fluid Mech., 1993, 256:85-106. |
| [12] | Wu X. On critical-layer and diffusion-layer nonlinearity in the three-dimensional stage of boundary-layer transition[J]. Proc. R. Soc. Lond., 1993, A433:95. |
| [13] | Li Jia. The numerical simulation of transition for spanwise wavepacket disturbances in boundary layers and the prediction by the PSE methed[D].[PhD Thesis]. Tianjin:Tianjin University, 2012.(in Chinese)李佳.边界层中展向波包型扰动转捩的数值模拟及用PSE方法转捩预测[D].[博士毕业论文].天津:天津大学, 2012. |
| [14] | Karniadkis G E, Israeli M, Orszag S A. High-order splitting methods for the incompressible Navier-Stokes equations[J]. J. Comput. Phy., 1991, 97:414-443. |
| [15] | Zhou Hen, Zhao Gengfu. Hydrodynamic Stability[M]. Beijing:National Defence Industry Press, 2004.(in Chinese)周恒,赵耕夫.流动稳定性[M].北京:国防工业出版社, 2004. |