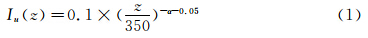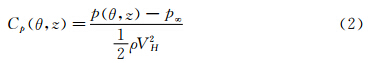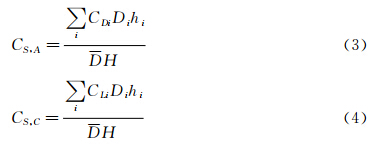2. 浙江省电力设计院, 浙江 杭州 310007
2. Electric Power Design Institute of Zhejiang Province, Hangzhou Zhejiang 310007, China
0 引 言
大型冷却塔通常在电厂中作为水冷却设备,其体型庞大,壁厚极薄,风荷载是主要荷载。1965年英国渡桥电站冷却塔群倒塌事件,引起人们对冷却塔干扰效应的重视。对于干扰效应,我国规范[1]认为满足规范的塔间距(塔中心距/塔底直径)要求时可以不考虑塔群影响;英国规范[2]给出1.5倍塔间距时脉动效应系数的修正因子;德国规范[3]基于气动弹性试验结果给出不同间距下的干扰因子。
由于塔间距对双塔干扰有较大影响,因此已有一些针对双塔进行干扰效应的研究。在风洞试验方面,张彬乾等[4]分析了冷却塔干扰时平均风压的变化;Orlando等[5]研究了三种排列情况下风压的干扰系数;Niemann等[6]采用气弹模型试验研究了薄膜应力的干扰效应;沈国辉等[7, 8]分析了阻力系数、升力系数随塔间距的变化;张军锋等[9]研究了风压干扰因子和等效风荷载比例系数随塔间距的变化。在CFD数值模拟方面,刘若斐等[10]分析了受干扰冷却塔的压力系数变化;沈国辉等[11]探讨了阻力系数随塔间距和风向角的变化规律。以上研究成果中塔间距范围较大,为1.3~2.5[7],而设计中[1]塔间距通常在1.5附近。参考国内外已建塔的塔间距资料,发现基本在1.4~1.6之间,因此本文着重研究工程常见塔间距(1.4~1.6)情况下的双塔干扰效应。同时干扰系数的基准从原来研究[4, 5, 6, 7, 8, 9, 10, 11]的某个或某两个效应推广到剪力系数、弯矩系数、径向位移、周向薄膜力和子午向薄膜力等。
基于以上背景,本文采用风洞试验的同步测量技术获得双塔情况下冷却塔外表面的风压,通过增加模型表面粗糙度的方法补偿模型试验的雷诺数效应,基于有限元方法进行各种工况的风致响应计算,最后通过分析基于整体风荷载指标(顺风向塔底剪力系数、弯矩系数和横风向塔底剪力系数、弯矩系数)和风致响应指标(径向位移、周向薄膜力和子午向薄膜力)的干扰系数,进行了双塔干扰效应研究。 1 风洞试验简介
某冷却塔高180 m,塔顶半径44.05 m,底部半径72.7 m,喉部高135 m,喉部半径40.76 m,塔底由48对均匀分布的人字柱支撑。布置14层外压测点,高度分别为178 m、172 m、163 m、149 m、135 m、121 m、107 m、93 m、79 m、65 m、51 m、37 m、23 m和14 m,每层沿环向均匀布置36个测点,共布置504个测点。冷却塔模型按1∶300缩尺比制作,双塔情况下的试验情况如图 1所示。
 |
| 图 1 冷却塔的风洞试验照片Fig. 1 Cooling tower picture in wind tunnel |
试验在浙江大学的ZD-1边界层风洞中进行的,试验段长18 m,宽4 m、高3 m。根据荷载规范要求,A类地貌大气边界层的平均风速剖面按指数规律变化。对于湍流度剖面Iu,参考日本AIJ规范[13]:
式中z为高度,α为地面粗糙度指数,对于A类地貌取0.12。在风洞中采用尖劈和粗糙元模拟边界层地貌,风洞模拟的平均风速和湍流度剖面如图 2所示,图中平均风速剖面以塔顶高度的风速进行无量纲处理,可见风洞中很好地模拟了A类地貌的边界层。风压测量采用美国Scanivalve扫描阀公司的电子扫描阀,对504个测点进行同步测压。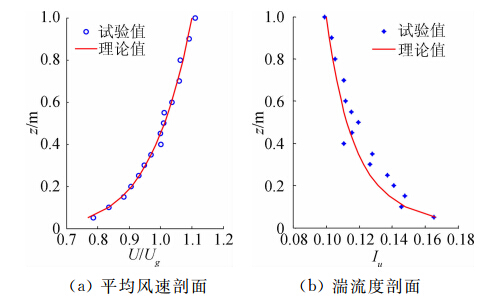 |
| 图 2 风洞试验模拟的平均风速和湍流度剖面Fig. 2 Simulated profiles of mean velocity and turbulence intensity |
风压系数Cp以塔顶高度H的速度压作为参考:
式中p(θ,z)是测点的压力值,p∞为参考点的静压值,θ为圆周角,ρ为空气密度,VH为塔顶高度的风速。冷却塔为圆形截面,假设沿i测层均匀分布N个风压测点,沿截面进行累加[7]可以得到顺风向的层阻力系数CDi和层升力系数CLi,根据各层的阻力系数和升力系数可以得到冷却塔整体的系数,其中冷却塔顺风向底部剪力系数CS,A、横风向底部剪力系数CS,C的计算公式为:
式中Di为i测层的截面直径,hi为i测层所占的竖直高度,D为冷却塔的平均直径。顺风向底部弯矩系数CM,A、横风向底部弯矩系数CM,C可分别如下计算:
式中αi为i测层塔表面外法线与水平面的夹角,Hi为i测层离底面的高度。风洞试验中由于试验设备的限制,在风洞中同步测压的测点数量受到一定的限制,为获得更多的风压时程数据,采用POD方法重构和加密冷却塔表面的风场。试验时模型表面沿高度布置14层,每层沿环向均匀布置36个测点,共布置504个测点,经POD方法插值加密后,风压点数变为40层×72个,总风压点数为2880个。将重构和加密后的数据用于式(3)~式(6)的计算。 3 模型表面粗糙度的选取
风洞试验的雷诺数与实际结构往往相差两个数量级,对于圆形截面的冷却塔,雷诺数的影响非常大,因此需要采用一定的方法来补偿模型试验的雷诺数。Sun等[14]、沈国辉等[15]和董锐等[16]均成功采用提高模型表面粗糙度的方法来补偿模型试验的雷诺数效应,本次试验也采用在模型表面粘贴粗糙条的方法来提高表面的粗糙度。
在模型外表面沿子午线方向均匀粘贴粗糙条,粗糙条厚度分别为0.8 mm、0.6 mm、0.4 mm、0.2 mm、0.1 mm和0 mm(光滑),粗糙条条数为36条。图 3给出厚度为0.4mm时喉部高度的体型系数μsi分布,体型系数的计算公式如下:
式中μzH为参考点的风压高度变化系数,μzi为测点的风压高度变化系数。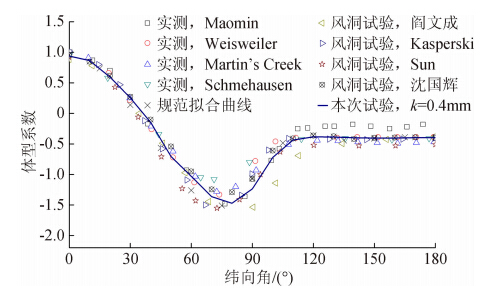 |
| 图 3 本次试验与规范、以往实测和试验值的比较Fig. 3 Data comparisons between present tests with codes, full-scale tests and others′ wind tunnel tests |
在图 3中将现场实测结果、相近试验条件的模型试验结果和规范数据绘于图中以进行比较,由图可知厚度取为0.4mm时数据较为合适,该数据与规范、以往实测和试验等都较为接近,在后面的双塔试验中均采用该粗糙度。 4 双塔干扰的数据分析
进行双塔干扰的风洞试验,测压塔、干扰塔的平面布置如图 4所示。两塔中心连线与来流风向的夹角为风向角θ,0°~180°风向角每隔7.5°为一个工况;取工程常见塔间距LD(塔中心距/塔底直径)为1.4~1.6,每隔0.05为一个工况,共125种工况。如下定义干扰系数IF,其中响应包括整体风荷载指标(顺风向塔底剪力系数、弯矩系数和横风向塔底剪力系数、弯矩系数)和风致响应指标(径向位移、周向薄膜力和子午向薄膜力)等。同时各响应的极大值采用平均值与3倍标准差之和来计算。
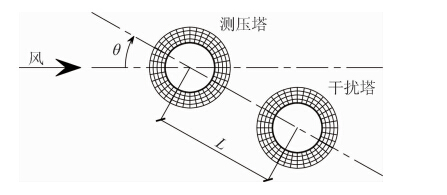 |
| 图 4 双塔风洞试验的平面布置示意图Fig. 4 Plane sketch of two cooling towers in wind tunnel |
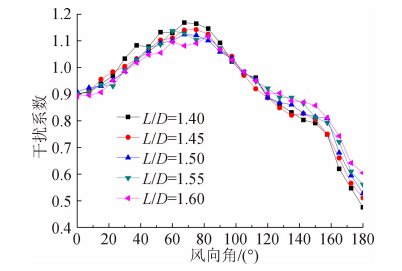
图 5给出了顺风向塔底剪力均值的干扰系数,由 图可知干扰系数与风向角的关系为:1)当0°≤θ≤30°时,由于后部干扰塔的存在导致处于上风向的测压塔尾流区的吸力作用降低,使得干扰系数小于1,但总体上在0.9~1.0之间;2)当37.5°≤θ≤105°时,由于双塔并行放置产生的“狭缝效应”,使得干扰系数大于1,在θ=67.5°附近取得极大值,最大数值约为1.15;3)当112.5°≤θ≤180°时,测压塔受到上风向干扰塔的尾流干扰作用,干扰系数小于1,当测压塔完全处于干扰塔正后方(即θ=180°)干扰效应取到最小值,干扰系数在0.55附近。
 |
| 图 5 顺风向塔底剪力均值的干扰系数Fig. 5 IF of mean base shears in along-wind direction |
由图 5还可以发现双塔干扰与塔间距的关系:1)虽然塔间距对干扰效应有一定的影响,但风向角与干扰系数的变化规律密切相关;2)当0°≤θ≤30°时,测压塔处于干扰塔的上风向,5种塔间距下的干扰系数总体比较接近;3)当37.5°≤θ≤105°时,两塔形成一定的“狭缝效应”,干扰系数大于1,此时塔间距越小,干扰系数越大,L/D=1.40时取到最大值,说明此时两塔越接近,狭缝效应越显著,干扰效应也越显著;4)当112.5°≤θ≤180°时,测压塔位于干扰塔的下风向,此时塔间距越小,干扰系数越小,说明此时两塔越接近,后塔(测压塔)受到前塔(干扰塔)的遮挡效应越显著,那么后塔所受的风荷载越小,在L/D=1.40时干扰系数取到最小值。
图 6给出了顺风向塔底剪力极大值的干扰系数。由图 6可知其变化趋势和顺风向塔底剪力均值干扰系数(见图 5)的变化趋势很相似,尤其是干扰系数随风向角的变化规律。由于极大值是考虑了脉动分量的因素,因此干扰系数随塔间距的变化趋势没有平均值干扰系数那么明显。
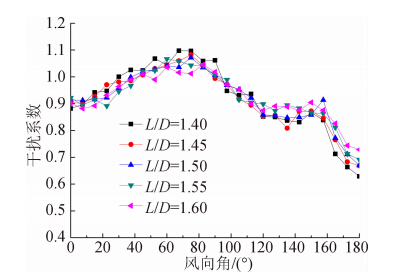 |
| 图 6 顺风向塔底剪力极大值的干扰系数Fig. 6 IF of peak base shears in along-wind direction |
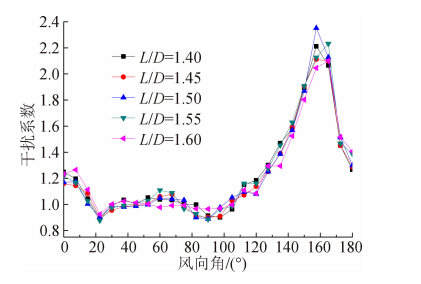 |
| 图 7 横风向塔底剪力系数极大值的干扰系数Fig. 7 IF of peak base shears in crosswind direction |
冷却塔在单塔情况横风向塔底剪力系数均值为0,故无法计算剪力系数均值的干扰系数。但可以计算横风向塔底剪力极大值的干扰系数,如图 7所示,可以发现:1)在0°≤θ≤15°,干扰系数略大于1,主要是由于位于下风向的干扰塔一定程度提高了测试塔横风向脉动;2)在22.5°≤θ≤105°,干扰系数基本上在1附近,说明左右排列情况对横风向的脉动没有增加;3)在112.5°≤θ≤180°,干扰系数明显大于1,测压塔位于干扰塔的侧后方,受干扰塔的尾流干扰作用,测试塔横风向的脉动得到很大的提升,在θ=165°时,横风向剪力极大值的干扰系数达到极大值,最大值接近2.3。 4.2 塔底弯矩干扰效应
图 8给出了顺风向塔底弯矩均值的干扰系数,可以发现该曲线与图 5基于剪力均值的干扰系数在曲线分布和数值上都比较接近,获得的结论也比较一致。同时图 9和图 10分别给出顺风向和横风向塔底弯矩极大值的干扰系数,也可以发现和图 6和图 7的分布比较一致,说明从干扰效应层面上而言,基于塔底弯矩和基于塔底剪力的计算结果比较一致。
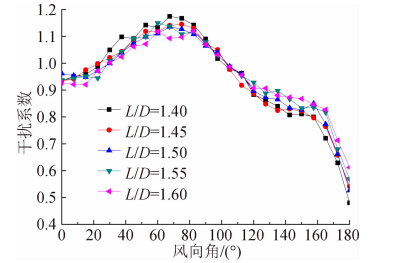 |
| 图 8 顺风向塔底弯矩均值的干扰系数Fig. 8 IF of mean base bending moments in along-wind direction |
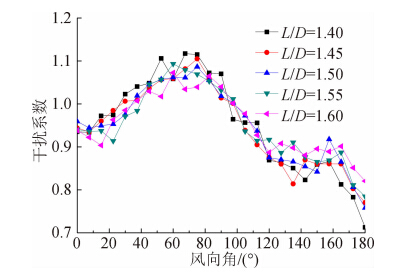 |
| 图 9 顺风向塔底弯矩系数极大值的干扰系数Fig. 9 IF of peak base bending moments in along-wind direction |
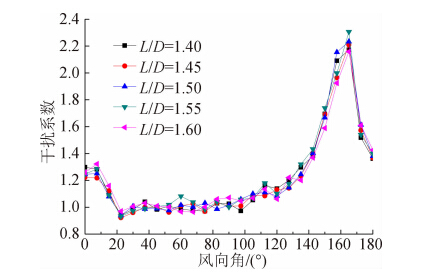 |
| 图 10 横风向塔底弯矩系数极大值的干扰系数Fig. 10 IF of peak base bending moments in crosswind direction |
采用有限元软件ANSYS进行冷却塔的风致响应计算,冷却塔按实际尺寸建模,图 11为冷却塔的有限元模型。塔筒沿环向分为96段,子午向沿高度分为44段,总的壳体单元数为4224个;上部刚性环梁划为96个单元;底部48对人字柱中每根支柱分为10个梁单元,共有960个梁单元,人字柱下端采用固定支座条件。壳体采用SHELL181单元,梁采用BEAM188单元。只考虑风荷载作用,风压时程采用经POD方法处理过的风洞试验数据。
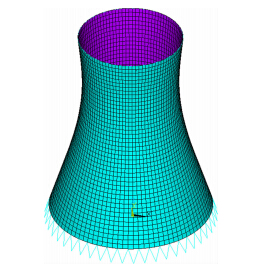 |
| 图 11 冷却塔的有限元模型Fig. 11 Finite element model of cooling tower |
 |
| 图 12 径向位移均值干扰系数Fig. 12 IF of mean axial displacements |
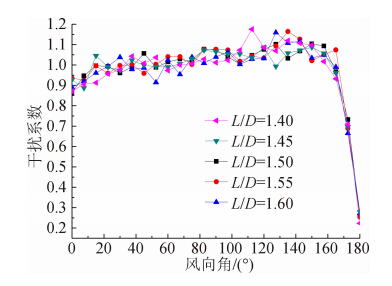
计算获得所有工况的风致响应,由于径向位移(朝内)、子午向薄膜力(拉力)和周向薄膜力(拉力)具有很好的参考作用,下面分别针对这3种响应进行分析。分析时取每种工况下冷却塔所有单元上的最大值进行考虑。
图 12给出径向位移(朝内)均值的干扰系数,可以发现:1)当风向角为0°≤θ≤22.5°和157.5°≤θ≤180°时,两者干扰系数小于1,其余风向角下干扰系数都比较稳定,在1~1.15之间,最大干扰系数出现的风向角在112.5°≤θ≤135°之间;2)在5种塔间距下干扰系数随塔间距的变化规律不明显,干扰效应随风向角变化也不如基于塔底剪力和塔底弯矩的明显;3)在θ=180°时干扰系数取到极小值,这是测压塔位于干扰塔的尾流区时,由于干扰塔的遮挡使得正风压变小所致,最小值接近0.2。
图 13给出径向位移(朝内)极大值的干扰系数。对比图 12可以发现:1)基于极大值的干扰系数与基于均值总体上比较接近,但基于极大值的数据更加离散,出现的风向角在112.5°≤θ≤135°之间;2)在θ=180°,基于极大值的干扰系数在0.6附近,而基于平均值的干扰系数约为0.25,存在一定的差异,主要是由于该风向角下测压塔位于干扰塔的尾流区,测压塔上风压的脉动有很大的提高所致。
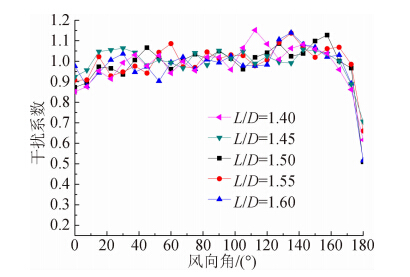 |
| 图 13 径向位移最大值干扰系数Fig. 13 IF of maximum axial displacements |
图 14和图 15分别为周向薄膜力(拉力)均值和极大值的干扰系数,可以发现:1)极大值的干扰系数较均值的干扰系数的波动大;2)当θ=180°时基于均值的干扰系数(图 14)最小值约为0.5,而基于极大值的干扰系数(图 15)最小值约为0.8,其差别原因和后塔的风压脉动提高有关;3)5种塔间距下干扰系数随塔间距的变化规律不明显;4)在风向角90°≤θ≤135°时,干扰效应较为显著,最大值接近1.2。
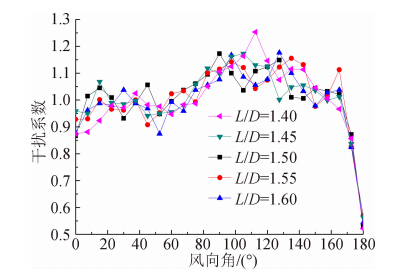 |
| 图 14 周向薄膜力均值干扰系数Fig. 14 IF of mean latitudinal membrane force |
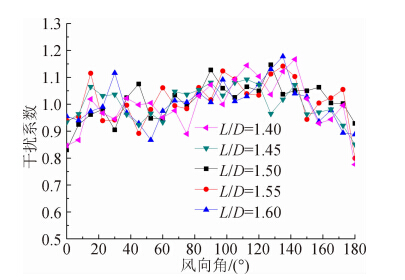 |
| 图 15 周向薄膜力最大值干扰系数Fig. 15 IF of maximum latitudinal membrane force |
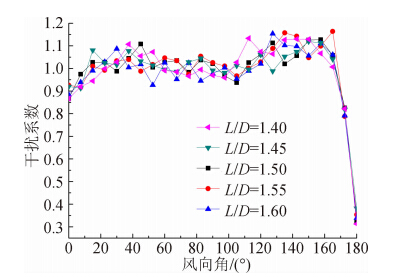 |
| 图 16 子午向薄膜力均值干扰系数Fig. 16 IF of mean meridian membrane force |
图 16和图 17分别为子午向薄膜力(拉力)均值和极大值的干扰系数,可以发现:1)子午向薄膜力(拉力)的干扰系数与径向位移(向内)的干扰系数比较接近,即图 16、图 17和图 12、图 13在数值和分布上都比较接近,其原因主要为两者都是出现在正迎风面上,两者具有一定的关联性;2)在127.5°≤θ≤150°时干扰系数相对较大,最大值接近1.15;3)当θ=180°时基于均值的干扰系数(图 16)最小值约为0.3,而基于极大值的干扰系数(图 17)最小值约为0.7,其差别原因和测压塔的风压脉动提高有关。
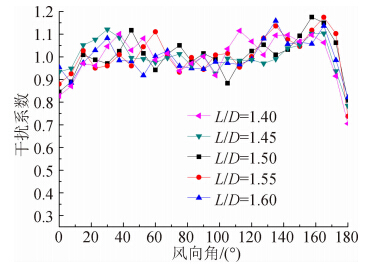 |
| 图 17 子午向薄膜力最大值干扰系数Fig. 17 IF of maximum meridian membrane force |
本文采用风洞试验和有限元方法研究工程常见塔间距下的双塔干扰,有以下几点结论:
(1) 从文中基于各种效应的干扰系数来看,除了基于横风向塔底剪力和弯矩极大值的干扰系数会达到2.3以外,基于其他效应的干扰系数最大值在1.15附近,因此本文认为在工程常见塔间距下双塔干扰系数最大值约为1.15。
(2) 从文中各干扰效应出现最大值的风向角来看,基于顺风向塔底剪力系数和弯矩系数约出现在67.5°风向,而基于风致响应指标(径向位移、周向薄膜力和子午向薄膜力)的最大值出现在90°≤θ≤150°之间的风向,两者存在一定的差别。
(3) 对顺风向塔底剪力而言,双塔并行放置时由于“狭缝效应”,使得干扰系数大于1,最大值约为1.15,此时塔间距越小,干扰效应越显著;而当测压塔处于前塔尾流区时,干扰系数小于1,此时塔间距越大,干扰效应越显著。
(4) 基于各种响应的干扰系数数据均表明:风向θ=0°和θ=180°时干扰系数均取得极小值。θ=0°时干扰塔位于测压塔的尾流中,对测压塔有一定的干扰;在θ=180°时,测压塔完全处于干扰塔的尾流区,此时测压塔的变形和内力较小。
| [1] | GB/T 50102-2003. Code for design of cooling for industrial recirculating water[S]. Ministry of Construction of the People's Republic of China. Beijing: China Plan Press, 2003. (in Chinese) GB/T 50102-2003. 工业循环水冷却设计规范[S]. 中华人民共和国建设部. 北京: 中国计划出版社, 2003. |
| [2] | BS4485(Part 4). Code of practice for structural design and construction-water cooling tower[S]. London: British Standard Institution, 1996. |
| [3] | VGB-R 610Ue. VGB-Guideline: structural design of cooling towers-technical guideline for the structural design, computation and execution of cooling towers[S]. Essen: BTR Bautechnik Bei Kuhlturmen, 2005. (in English) |
| [4] | Zhang Binqian, Li Jianying, Yan Wencheng. Investigation on interrelation of wind load for double super large hyperbolic cooling tower[J]. Experiments and Measurements in Fluid Mechanics, 2003, 17(Special Issue): 93-97. (in Chinese) 张彬乾, 李建英, 阎文成. 超大型双曲冷却塔双塔干扰的风荷载特性研究[J]. 流体力学试验与测量, 2003, 17(特刊): 93-97. |
| [5] | Orlando M. Wind-induced interference effects on two adjacentcooling towers[J]. Engineering Structures, 2001, 23: 979-992. |
| [6] | Niemann H J, Kopper H D. Influence of adjacent buildings on wind effects on cooling towers[J]. Engineering Structures, 1998, 20(10): 874-880. |
| [7] | Shen Guohui, Yu Guanpeng, Sun Bingnan, et al. Study of interference effects of two large hyperbolic cooling towers by using wind tunnel test[J]. Journal of Vibration and Shock, 2011, 30(3): 109-114. (in Chinese) 沈国辉, 余关鹏, 孙炳楠, 等. 大型冷却塔双塔干扰的风洞试验研究[J]. 振动与冲击, 2011, 30(3): 109-114. |
| [8] | Shen Guohui, Yu Guanpeng, Sun Bingnan, et al. Study of wind-induced interference effects on three adjacent cooling towers under upside-down triangular distribution[J]. Acta Aerodynamica Sinica, 2011, 29(1): 107-112. (in Chinese) 沈国辉, 余关鹏, 孙炳楠, 等. 倒品字形分布三个冷却塔的风致干扰效应研究[J], 空气动力学学报, 2011, 29(1): 107-112. |
| [9] | Zhang Junfeng, Zhao Lin, Ke Shitang et al. Wind tunnel investigation on wind-pressure interference effects for tow large hyperboloidal cooling towers[J]. Journal of Harbin Institute of Technology, 2011, 43(4): 81-87. (in Chinese) 张军锋, 赵林, 柯世堂, 等. 大型冷却塔双塔组合表面风压干扰效应试验[J]. 哈尔滨工业大学学报, 2011, 43(4): 81-87. |
| [10] | Liu Ruofei. Study on wind-resistant behaviors of large hyperbolic cooling tower[D]. Hangzhou: Zhejiang University, 2006. (in Chinese) 刘若斐. 大型冷却塔的抗风研究[D]. 杭州: 浙江大学, 2006. |
| [11] | Shen Guohui, Liu Ruofei, Sun Bingnan. Numerical simulation of wind load on cooling towers under double-tower condition[J]. Journal of Zhejiang University (Engineering Science), 2007, 41(6): 1017-1022. (in Chinese) 沈国辉, 刘若斐, 孙炳楠. 双塔情况下冷却塔风荷载的数值模拟[J]. 浙江大学学报(工学版), 2007, 41(6): 1017-1022. |
| [12] | Tamura Y, Suganuma S, Kikuchi H, et al. Proper orthogonal decomposition of random wind pressure field[J]. Journal of Fluids and Structures, 1999, 13: 1069-1095. |
| [13] | Architectural Institute of Japan. Recommendations for loads on buildings[S]. Tokyo: Architectural Institute of Japan, 2004. |
| [14] | Sun T F, Zhou L M. Wind pressure distribution around a ribless hyperbolic cooling tower[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1983, 14: 181-192. |
| [15] | Shen Guohui, Yu Guanpeng, Sun Bingnan, et al. The influence of modal surface roughness on wind loads of cooling towers[J]. Engineering Mechanics, 2011, 28(3): 86-93. (in Chinese) 沈国辉, 余关鹏, 孙炳楠, 等. 模型表面粗糙度对冷却塔风荷载的影响[J]. 工程力学, 2011, 28(3): 86-93. |
| [16] | Dong Rui, Zhao Lin, Ge Yaojun, et al. Investigation of surface roughness and its influence to flow dynamic characteristics of hyperbolic cooling tower[J]. Acta Aerodynamica Sinica, 2013, 31(2): 250-259. (in Chinese) 董锐, 赵林, 葛耀君, 等. 双曲圆截面冷却塔壁面粗糙度对其绕流动态特性影响[J]. 空气动力学学报, 2013, 31(2): 250-259. |