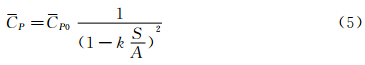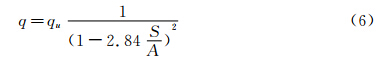0 引 言
风洞试验是结构风工程研究的重要手段之一。在风洞中模拟建筑的真实风环境,以确定建筑的气动力特性和周围的流场特性。建筑风洞通常是闭口直流式或闭口回流式,以壁面为边界,而实际建筑在大气流场中并无边界。用风洞的有限空间来模拟实际大气的无限空间必然伴随着洞壁干扰,造成建筑气动力和流场方面的差别。此外,结构风工程的研究对象多为钝体,当气流流经建筑时会产生较为宽阔的侧面绕流和尾流,从而阻塞效应尤为显著。风洞壁面对气流绕流的约束称为“实体阻塞”,对尾流的约束称为 “尾流阻塞”,上述两种洞壁干扰即为阻塞效应[1]。
至今涉及建筑结构风洞试验阻塞效应的研究较少。一些学者[2, 3, 4, 5, 6]在相同风洞中变化二维方柱模型缩尺比,分别提出二维方柱阻力系数的修正公式,但试验条件和公式形式各不相同,无法为三维模型的阻塞修正提供指导。也有少数学者对三维模型阻塞效应研究。Hunt[7]对湍流边界层流场中的立方体模型进行测压试验表明,8%的阻塞度对平均风压的影响不足2%,对脉动风压的影响不足10%。作者指出对于低矮建筑最大容许的阻塞度为10%。徐永定和吕录勋[8, 9]对切角三角形高层建筑分别进行测力和测压试验,研究了不同来流风向角和湍流度下的阻塞效应。谢壮宁等[10]对三种缩尺比的低矮房屋标准模型进行了测压对比试验,认为当阻塞度为4.9%时,阻塞效应不能忽视。Wang等[11]基于某高层建筑实际工程项目,对两种缩尺比的刚性测压模型进行风洞试验,比较了建筑表面平均和脉动风压系数。
关于建筑模型风洞试验阻塞效应虽然有一定的研究,但至今并没有获得风工程研究人员的广泛认识,也未有公认的阻塞修正方法。本文以不同缩尺比的单体矩形高层建筑模型为试验对象,在低湍流均匀流中研究了模型表面平均风压特性。对比了各模型迎风面、侧面、背风面和顶面的平均风压系数。采用二维方柱的修正方法对试验结果进行修正。修正结果表明,二维方柱的修正方法并不能很好地适用于本试验结果。在Peitzman方法的基础上提出了适用于本试验的平均风压系数阻塞效应修正公式。 1 风洞试验概况 1.1 风场模拟
试验在同济大学土木工程防灾国家实验室风洞试验室TJ-2大气边界层风洞中完成。该风洞试验段长15m,宽3m,高2.5m,风速为0.5~60m/s连续可调。在不同缩尺比模型试验时采用相同的均匀风 场,控制来流风速为14m/s。图 1为风洞空载时拟 安装模型位置处的平均风速和湍流度剖面。由于风洞边界层的影响,0.3m以下的区域内平均风速和湍流度剖面的均匀性不如上部。
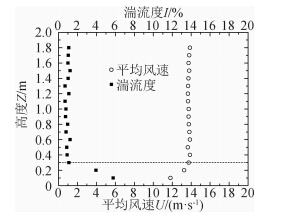 |
| 图 1 平均风速和湍流度剖面Fig. 1 Mean wind speed and turbulence profile |
风洞试验模型采用4种缩尺比,阻塞度变化范围为4.1%~10.1%。模型尺寸见表 1。各模型的测点布置图见图 2~图 4。图 5为风洞试验中基本坐标的定义。图 6为俯视图及各面命名。本文仅在0°风向角(模型宽面迎风)的情况下进行数据分析。
缩尺比 | 模型编号 | Dx /mm | Dy /mm | H /mm | 宽面迎风 阻塞度/% |
| 1∶165 | M1 | 185 | 277 | 1108 | 4.1 |
| 1∶135 | M2 | 226 | 339 | 1355 | 6.1 |
| 1∶115 | M3 | 265 | 398 | 1590 | 8.4 |
| 1∶105 | M4 | 290 | 435 | 1742 | 10.1 |
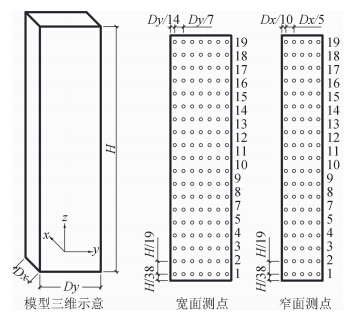 |
| 图 2 模型立面及测点布置Fig. 2 Vertical view of the model and tap arrangement |
 |
| 图 3 层测点布置Fig. 3 Tap arrangement of layers |
 |
| 图 4 顶面测点布置Fig. 4 Tap arrangement on the top |
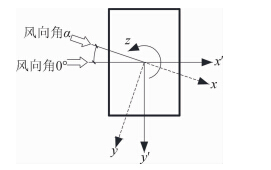 |
| 图 5 基本坐标定义Fig. 5 Definition of the basic coordinate |
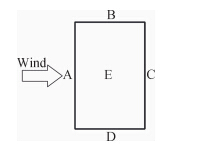 |
| 图 6 俯视图及各面命名Fig. 6 Top view and name of surface |
试验模型采用5mm厚有机玻璃板制作,测点直径为1.1mm,测压管与扫描阀之间用PVC管连接。测压管长度均采用1m,以避免测压管长度不同或管道过长所带来的误差。试验数据采用相同的管道函数来修正[12]。 2 试验数据分析 2.1 平均风压系数
各测点平均风压系数为:
式中,Pi为第i点的平均风压系数; 为第i点的平均风压;ρ为空气密度;UH为模型高度位置的平均风速。为方便分析,将各模型的平均风压系数与模型M1的平均风压系数差值与M1的平均风压系数之比称为各模型平均风压系数的相对差值:
式中,SMi为模型Mi的平均风压系数,i=2~4。图 7为模型各面平均风压系数,图中横坐标为测点序号,A、C面每层7个测点,B、D面每层5个测点,E面共35个测点,布置方法可参见图 2~图 4。图 7(a)和图 7(c)中,测点1~7为第一层,测点8~14为第二层,以此类推。图 7(b)中,测点1~5为第一层,测点6~10为第二层,以此类推。对于迎风面A面测点,在较低的位置,M1的平均风压明显低于其它模型,主要由于边界层的影响;在整个高度上,迎风面平均风压系数受阻塞度的影响幅度较小。对于侧面、背风面和顶面,随着阻塞度增加平均风压系数明显降低,但各表面平均风压系数的分布规律并没有改变。
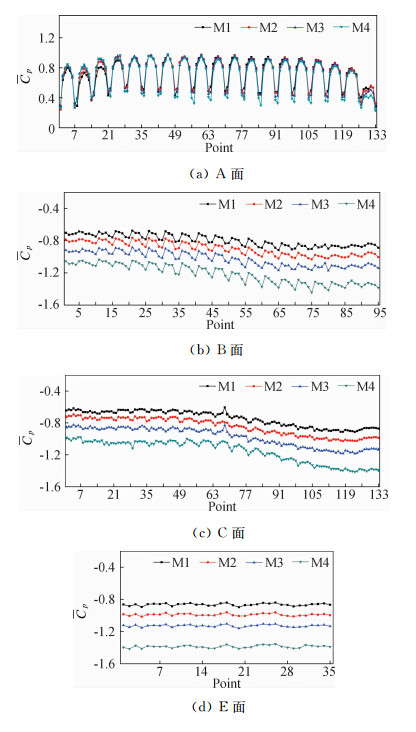 |
| 图 7 模型表面平均风压系数Fig. 7 Mean pressure coefficient on model surfaces |
图 8为模型各面平均风压系数与M1的相对差值。对于迎风面A面测点,模型M1~M4在较低位置、最高层和角部测点的相对差值较大,在其它位置的相对差值较小。在同一阻塞度时,侧面、背风面和顶面平均风压系数的相对差值都接近同一数值,阻塞度越大相对差值越大。但对于模型M4,侧面和背风面的平均风压系数的相对差值的在整个表面上的一致性不如模型M2和M3。
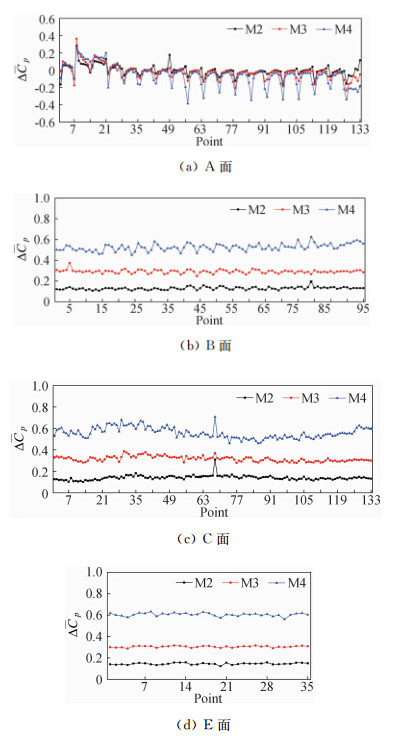 |
| 图 8 模型表面平均风压系数相对差值Fig. 8 Relative difference of mean pressure coefficient on model surfaces |
表 2列出了各模型迎风面、侧面、背风面和顶面平均风压系数相对差值的均值。由于边界层影响,仅对10层以上的测点进行统计。在计算迎风面测点相对差值时每层靠近边缘的两个测点和19层测点不统计。由表可知,阻塞效应对模型迎风面平均风压系数的影响不足5%,但侧面、背风面和顶面的阻塞效应比较明显。对比于阻塞度为4.1%的模型M1,当阻塞度为6.1%时,各面平均风压系数的相对差值为13.4%~14.5%;当阻塞度为8.4%时,各面平均风压系数的相对差值为29.2%~30.5%;当阻塞度为10.1%时,各面平均风压系数的相对差值为52.9%~60.5%。可见,对于较大阻塞度的模型,负压区测点平均风压已产生较大的畸变。
| 模型 | A面 | B面 | C面 | D面 | E面 |
| M2 | -1.2 | 13.4 | 13.8 | 14.0 | 14.5 |
| M3 | -2.1 | 29.1 | 30.2 | 29.1 | 30.5 |
| M4 | -4.7 | 53.9 | 52.9 | 54.0 | 60.5 |
试验中的平均风速为14m/s,模型的雷诺数范围为Re=1.46×105~4.17×105,属于同一量级。并且对于本文矩形柱这样的带有尖角的钝体,分离点固定在迎风前缘的角部位置,且模型截面长宽比较小不会发生再附,所以雷诺数的影响可忽略[13]。在风场方面,试验采用均匀流场,排除了来流给试验结果带来的差别。所以,阻塞效应是上述结果差别的主要原因。 2.2 试验中皮托管的压力
试验中模型位置附近安装两个皮托管: Pitot_1安装于模型前方2.5m处的风洞壁面,距地面1.8m;Pitot_2安装于模 型前方1m处的风洞顶面,距地面2.2m。
表 3为试验时风洞中皮托管处的平均风速和动压的相对差。其中相对差值的计算参考式(2)。由表 3可知,Pitot_1处的平均风速受阻塞度影响较小;Pitot_2处的平均风速随着阻塞度的增加而增大。由Pitot_2处动压的相对差可见,在所有阻塞度下,动压的增幅均在4%以内。对比表 3和表 2可知,阻塞效应所引起的模型表面平均风压系数的增大远大于参考点动压的增大,参考动压的变化并不足以修正阻塞效应。
模型 | Pitot_1处风速 /(m·s-1) | Pitot_2处风速 /(m·s-1) | Pitot_2动压 相对差/% |
| M1 | 13.9 | 14.2 | - |
| M2 | 13.9 | 14.3 | 1.7 |
| M3 | 13.9 | 14.4 | 3.2 |
| M4 | 13.8 | 14.5 | 3.5 |
对于类似于本文模型的钝体结构的风洞试验阻塞度修正方法主要有两种:Maskell法[14]和Peitzman法[15]。
Maskell法是根据动量定理辅以经验关系导出的修正公式:
式中,q为经过阻塞度修正后的模型处的动压力;qu为风洞空载时流经模型处的动压力; S A 为阻塞比;Cxu为试验测得的模型阻力系数。Peitzman法是根据质量守恒定理推导,并进行简化的修正公式:
上述两种方法本质是一致的,均认为阻塞效应引起了模型处的风速增大。Maskell法在参考动压修正时,除了考虑阻塞度外还将试验测得的阻力系数作为参数。图 9为模型2/3H处测点平均风压系数采用上述方法修正的结果,仅对侧面和背风面平均风压系数修正。由图可见,经过Maskell法修正后,不同阻塞度下侧面和背风面的风吸力的差异有所改善,但仍有一些差别;Peitzman法对阻塞效应的估计不足,各组数据间差别较大。总体看来,两种方法对平均风压系数的修正结果并不理想,需要发展更好的修正方法。
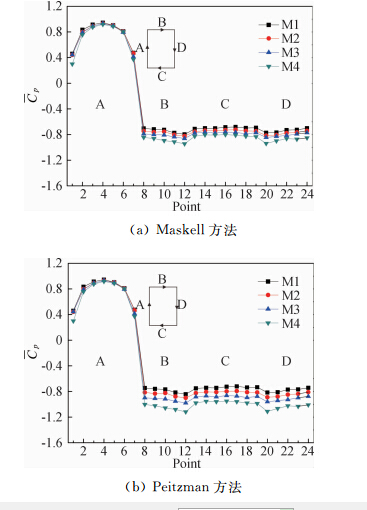 |
| 图 9 模型2/3H测点平均风压系数修正结果Fig. 9 Correction of mean pressure coefficient on 2/3H of the model |
由于Peitzman方法形式简单,原理易于理解,将其作进一步修正,提出适合于本文试验的平均风压系数的阻塞效应修正公式。根据前面的分析,在Peitzman法中引入阻塞效应调整因子k,公式如下所示:
式中,C P0为排除阻塞效应的模型表面平均风压系数;C P为风洞试验获得的模型表面平均风压系数;k为待定参数。迎风面测点无需修正,通过式(5)对模型侧面、背风面和顶面测点的数据最小二乘拟合,得到相应参数。基于1/2H高度以上平均风压系数拟合参数,结 果见于图 10。由图可见,各面不同测点的拟合结果较为接近。对图 10中相同面上测点的参数拟合结果进行了平均处理,结果见于表 4中。由表 4可见,各面拟合的参数差别较小。为了方便实际应用,将k取为平均值2.84。新的修正公式可表示为:
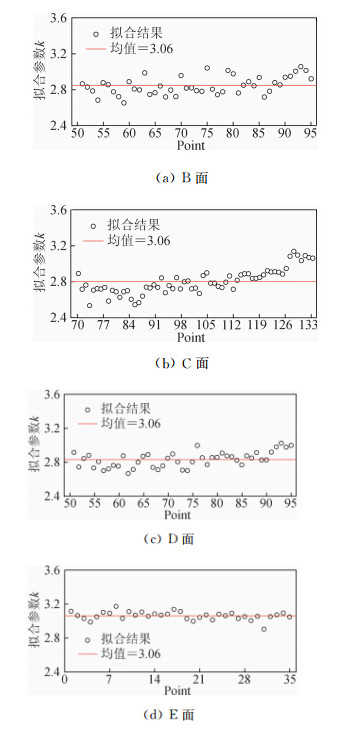 |
| 图 10 参数k的拟合结果Fig. 10 Parameter fitting of k |
| 参数 | B面 | C面 | D面 | E面 |
| k | 2.84 | 2.80 | 2.83 | 3.06 |
采用式(6)分别对0°和90°风向角下2/3H处测点平均风压系数修正,修正结果示于图 11中,可见修正结果较为满意。
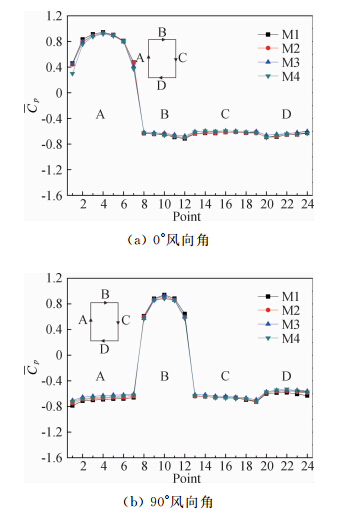 |
| 图 11 模型2/3H处平均风压系数 Peitzman改进方法修正结果Fig. 11 Corrected mean pressure coefficient on 2/3H of the model by improved Peitzman method |
本文通过刚性模型测压试验,研究了阻塞效应对均匀流场中单体矩形高层建筑表面平均风压系数的影响,主要结论如下:
(1) 模型迎风面平均风压系数随阻塞度的增大有所减小,除最接近角部位置测点影响较大外,迎风面平均风压系数的影响不足5%,可忽略;
(2) 模型侧面、背风面和顶面平均风压系数受阻塞效应的影响较大,阻塞度越大平均风压系数明显降低。对比于阻塞度为4.1%的模型,当阻塞度为6.1%、8.4%和10.1%时,各面平均风压系数的增幅分别为13.4%~14.5%、29.2%~30.5%和52.9%~60.5%。但阻塞效应没有显著影响平均风压系数的分布规律;
(3) 依据现有试验数据,提出了单体矩形高层建筑模型表面平均风压的阻塞效应修正公式,修正结果较为满意。
| [1] | Cheng Houmei. Wind tunnel experiment interference and correction[M]. Beijing:National Defence Industry Press, 2003. (in Chinese) 程厚梅. 风洞实验干扰与修正[M]. 北京: 国防工业出版社, 2003. |
| [2] | Raju K G R, Singh V. Blockage effects on drag of sharp-edged bodies[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1975, 1(3): 301-309. |
| [3] | Awbi H B. Wind-tunnel-wall constraint on two-dimensional rectangular-section prisms[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1978, 3(4): 285-306. |
| [4] | Laneville A, Trepanier J Y. Blockage effects in smooth and turbulent flows: the case of two-dimensional rectangular cylinders[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1986, 22(2-3): 169-176. |
| [5] | Laneville A. Turbulence and blockage effects on two dimensional rectangular cylinders[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1990, 33(1-2): 11-20. |
| [6] | Noda M, Utsunomiya H, Nagao F. Basic study on blockage effects in turbulent boundary layer flows[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1995, 54/55: 645-656. |
| [7] | Hunt A. Wind tunnel measurements of surface pressures on cubic building models at several scales[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1982, 10(2): 137-163. |
| [8] | Xu Yongding, Lyu Luxun. Wind tunnel wall blockage effects on corner cut triangular prisms[J]. Aerodynamic Experiment and Measurement & Control, 1987, 1(2): 21-26. (in Chinese) 徐永定, 吕录勋. 切角三角形柱体模型的洞壁阻塞干扰研究[J]. 气动实验与测量控制, 1987, 1(2): 21-26. |
| [9] | Xu Yongding, Lyu Luxun. Wind tunnel wall blockage effects on pressure distributions of hexagonal prisms[J]. Aerodynamic Experiment and Measurement & Control, 1989, 3(3): 21-25. (in Chinese) 徐永定, 吕录勋. 多角柱体表面压力洞壁阻塞干扰的试验研究[J]. 气动实验与测量控制, 1989, 3(3): 21-25. |
| [10] | Xie Zhuangning, Liu Shuai, Shi Biqing. Investigation into wind tunnel test of standard low-rise building model[J]. Journal of South China University of Technology (Natural Science Edition), 2011, 39(6): 106-112. (in Chinese) |
| [11] | Wang L, Liang S G, Tang H Q, et al. Investigation on wind tunnel blockage effect of super high-rise building[C]//The Seventh International Colloquium on Bluff Body Aerodynamics and Applications. Shanghai, China, 2012. |
| [12] | Zhou Xuanyi, Gu Ming. Optimization of dynamic pressure measurement of single-channel tubing systems[J]. Journal of Tongji University (Natural Science Edition), 2003, 31(7): 798-802. (in Chinese) 周晅毅, 顾明. 单通道测压管路系统的优化设计[J]. 同济大学学报(自然科学版), 2003, 31(7): 798-802. |
| [13] | Larose G L, D Auteuil A. On the Reynolds number sensitivity of the aerodynamics of bluff bodies with sharp edges[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2006, 94(5): 365-376. |
| [14] | Maskell E C. A theory for the blockage effects on bluff bodies and stalled wings in a closed wind tunnel[R]. ARC R&M 3400, 1963. |
| [15] | Peitzman F W. Low speed wind tunnel investigation to develop high attitude wall correction in the Northrop 7×10-foot low speed wind tunnel[R]. NOR 78-20, 1978. |