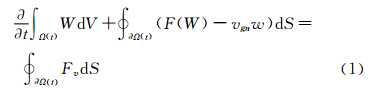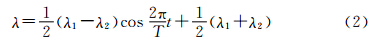0 引 言
随着科技的发展,对飞行器性能的要求不断提高。常规布局飞行器只能在某种状态下达到最优性能,一旦飞行条件改变,如大攻角、低空巡航、过失速机动状态,飞行器的性能就会变差,而变体飞行器由于可根据不同的飞行条件调节自身外形,从而改变飞行性能,因而越来越受到研究人员的重视。
变体飞行器是指能够在飞行中改变气动外形,如机翼面积、展弦比和后掠角等,使飞行器在不同飞行状态下均保持最佳性能[1]。与常规固定布局飞行器相比,变体飞行器的飞行包线更宽,作战效能更高,能够根据飞行环境、飞行剖面以及作战任务等需要,自主地改变气动构型,优化其飞行性能[2, 3]。
从变体飞行器的变形机理来看主要分为两类:虚拟的变体和真实的变体。
虚拟的变体主要是指利用流场主动控制技术使得飞行器的外界扰流发生变化。现已有很多代表性的方式,如采用合成射流技术[4, 5, 6]、流场吹吸气技术[7]、等离子体激励器技术[8]。其对于流动影响的结果相当于在飞行器上安装了虚拟的实体,从而改变流场结构,提高飞行器的性能。这种方式的优势之处在于对飞行器的气动外形改变不大,适合于在特定条件下改进飞行器的气动特性,如起飞、着陆状态。
真实的变体是指利用飞行器结构外形的改变,使流场重新分布,以提升飞行性能。在这方面已有很多活跃的主题。如:美国国防预研局(DAPPA)变形飞机结构(Morphing Aircraft Structure)研究项目中[9]洛克希德马丁公司提出的折叠机翼方案[10],通过采用整体式无缝折叠机翼,使后掠角改变30°,有效翼展增加71%,机翼面积增加180%,最大升阻比增加52%;新一代公司提出的滑动蒙皮机翼方案[11],采用特殊材料制作的柔性蒙皮实现了展长变化40%,机翼面积变化70%;任务自适应机翼(Mission Adaptive Wing)项目[12]中,通过采用光滑变前后缘弯度机翼,使得飞行器的巡航、机动性能得到了提升;智能机 翼(Smart Wing)项目[13]中,采用连续光滑无铰接大 偏角高速操纵面,获得了滚转和俯仰性能的提升。这种变形方式适合大幅改变飞行器的气动特性,使之在较大空域范围内获得良好的性能。
综合国内外的研究现状来看,以上两类变形机理均是研究人员关注的焦点。对虚拟的变体方式的研究已有数值仿真[4, 5, 6, 8]、风洞实验[6]的研究方法,而对于真实的变体方式,现有的研究成果多采用理论分析[14]与风洞实验[15, 16, 17]的方式进行研究,尚未见变体过程的非定常气动机理进行仿真分析。为研究飞行器变体过程的非定常气动特性,本文以柔性变后掠飞行器为研究对象,采用数值模拟方式分析变后掠过程典型状态下的定常气动特性,对柔性变后掠飞行器变后掠过程中的非定常气动力进行仿真,研究结果可为变后掠飞行器的动态特性分析与飞行控制系统设计提供参考依据。 1 柔性变后掠飞行器
本文研究对象为柔性变后掠飞行器,采用正常式布局,机翼后掠角可改变30°。图 1给出了柔性变后掠过程中机翼处于典型后掠角时的外形,机身为扁平流线型外形,采用V型垂尾,机身长2.3m,机翼半展长1.5m,弦长0.4m,机翼、垂尾、平尾均采用NACA2412翼型。
 |
| 图 1 柔性变后掠飞行器的典型外形Fig. 1 Typical shapes of flexible variable-sweep morphing aircraft |
为实现柔性变后掠过程,机翼经过特殊设计。机翼包括三部分结构:绕固定点转动的前缘,可进行“错动”运动的平行四边形中间结构,绕固定点转动的后缘。前缘和后缘由刚性结构组成,中间结构由翼肋、桁条、柔性蒙皮组成。机翼在变形过程中,各翼肋始终与机身轴线保持平行,各桁条分别绕内侧端点旋转,柔性蒙皮发生剪切变形[17]。文中所指的柔性变后掠过程即指错动运动的过程。
这样的柔性变形方式相对于刚性变形方式有如下好处:变形中始终保持顺流动方向翼型不变,保持了飞行器良好的气动性能;在翼身交接部位不需要为转动机翼开槽,降低了机身结构设计的复杂程度;若安装翼梢小翼,则翼梢小翼在变形过程中始终平行于机身轴线,不会带来附加阻力。 2 数值方法 2.1 流体控制方程的离散与求解
ALE (Arbitrary Lagrangian Eulerian)格式的非定常可压缩Navier-Stokes方程为:
式中,W=(ρ,ρu,ρv,ρw,ρe)T为守恒量,F(W)、Fv分别为无粘通量和粘性通量,vgn为控制体表面的法向运动速度,Ω(t)为任意时刻的控制体,dV为体积微元,dS为面积微元。为求解变后掠过程中的非定常气动力,空间上采用二阶迎风格式的有限体积法离散控制方程,时间推进采用一阶精度Runge-Kutta法,压力-速度耦合采用PISO算法,湍流计算选用单方程S-A模型,在应用变形动网格时还引入了几何守恒定律[18]。 2.2 算法验证
为了验证定常、非定常计算的精度,分别选用美国太阳能研究 所NACA4418翼型的实验值和北约航空发展与咨询组(AGARD)的Case 1进行CFD验证。对NACA4418翼型的定常气动特性和NACA0012翼型俯仰振荡中的气动特性进行数值仿真,并将计 算结果与实验值进行对比[19, 20]。计算中边界条件的选取与实验时相同,计算网格与升力系数随攻角变化曲线如图 2所示。
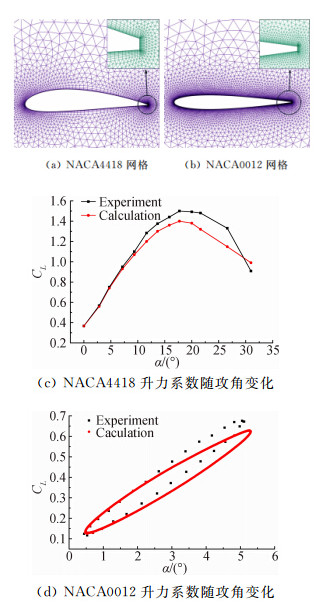 |
| 图 2 计算网格与升力系数随攻角变化曲线Fig. 2 Plot of grid around airfoil and lift coefficient varies with angle of attack |
由图 2可知,总体来看计算结果在小攻角时与实验值吻合较好,随攻角增大两者的差距有所增大,26°攻角时,定常计算值比实验值[20]偏小13.6%,非定常计算与定常计算结果相差很小。2°攻角时非定常计算值与实验值的偏差小于2%,均在可接受的误差范围内,说明算法满足研究需要。 2.3 运动参数定义
计算中后掠角的变化规律取为三角函数规律:
式中,λ为t时刻后掠角,λ1为最小后掠角,λ2为最大后掠角,T为运动周期。计算中,后掠角变化速率包括三种,分别对应T的三种取值。 2.4 网格划分与边界条件
通过对局部敏感区域进行加密,带有非结构网格的变后掠飞行器计算域,网格数量为220万,壁面附近的网格尺度为0.02m左右,并保证y+<5。流向方向取为飞行器长度的18倍,展向取为飞行器展长的13.8倍,机翼展向方向划分260个网格,并从机翼表面以1.2的增长率增长至远场。外边界选用压力远场边界条件,自由来流马赫数为0.0735,雷诺数为6.9×105,内部边界选用无滑移边界。计算中CFL数为15。为保证计算时的稳定性,将初始状态定常计算结果作为非定常计算的初值,并使三种变后掠速 率分别各计算5个周期,每步计算收敛至10-4以下量 级,取最后一个周期的结果进行分析。 3 结果分析 3.1 不同后掠角的定常气动特性
研究变后掠飞行器非定常气动特性之前,有必要先进行定常气动特性的计算,以了解不同后掠角对于飞行器气动特性的影响。图 3中显示了四种状态下气动特性随攻角变化曲线,计算结果表明:
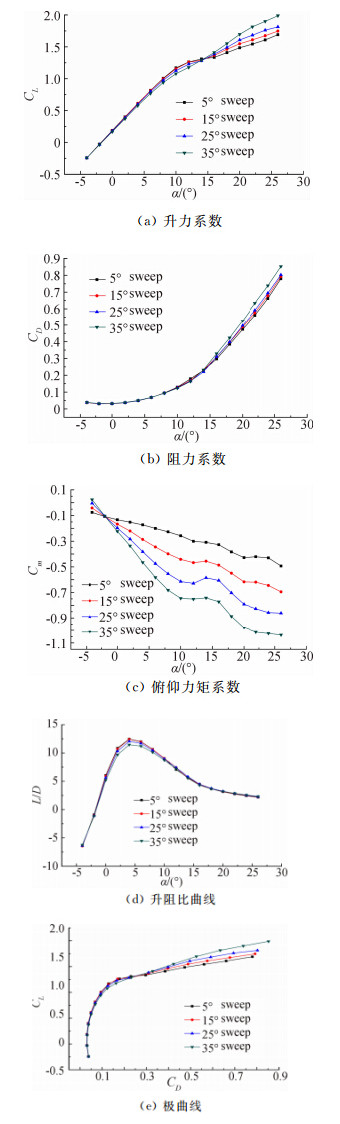 |
| 图 3 不同后掠角时的气动特性Fig. 3 Aerodynamic characteristics of different sweep angles |
(1) 升力系数随攻角增加而增大。攻角小于10°时,升力系数随攻角的增加而线性增长,10°至14°攻角时,升力系数的增加有所减缓,大于14°攻角,升力系数的增长又有所加快。进一步研究表明,攻角大于14°后,翼身组合体充当了主要升力体的作用,平尾对升力的增量也有一定贡献,此时垂尾上产生的升力基本维持不变。攻角小于14°时,在给定攻角下,升力系数随着后掠角增大而减小,攻角大于14°时,升力系数随着后掠角增大而增大。
(2) 阻力系数随攻角增加而增大。总体上看,攻角小于14°时,大的后掠角在同样的攻角下阻力系数更小,攻角大于14°时,同样的攻角下大的后掠角会带来更大的阻力系数。进一步研究发现,所有攻角下,随后掠角增加,阻力均在下降,阻力系数增加的原因是由于参考面积减小引起的。
(3) 俯仰力矩系数随攻角增大而减小,随后掠角增加而减小,表现为低头力矩加大。这是由于后掠角增大,使全机的气动中心后移造成的,随着后掠角的增加,飞行器的静稳定性也随之增强。
(4) 从升阻比随攻角的变化曲线可以看出,对于不同后掠角,飞行器均在4°攻角处取得最大升阻比,偏离此攻角,升阻比均呈下降趋势。最大升阻比随后掠角增大而减小,35°后掠角的最大升阻比较5°后掠角的最大升阻比小8.04%。
(5) 对比不同后掠角的极曲线可以看出,当升力系数小于1.28时,在同样的升力系数下,小后掠角的阻力系数较小,升力系数大于1.28后,大后掠角对应较小的阻力系数。
从以上分析可知,不同后掠角对应的气动特性有一定差异。因此变后掠飞行器可以利用这种差异,采用不同的外形,来达到实时最优的气动状态。 3.2 定常、非定常气动特性比较
动态变后掠过程中的非定常气动力与定常结果有何不同,这是我们所关心的问题。下面将对变后掠飞行器的非定常气动特性进行计算,与定常结果进行比较,以了解这种差异。
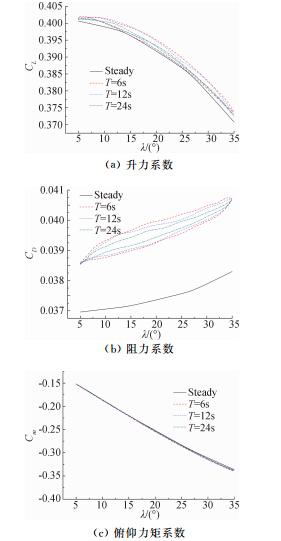
由之前的分析可知,变后掠飞行器在4°攻角时取得最大升阻比,因此选取接近最大升阻比的2°攻角对变后掠飞行器的非定常气动特性进行研究。规定后掠角增大过程为去程,后掠角减小过程为回程。选用三种变化周期分别为T=6s、12s、24s,计算变后掠过程中的气动力随后掠角变化情况。取最后一个周期的计算值,与定常计算结果比较,如图 4所示。
 |
| 图 4 气动特性随后掠角的变化Fig. 4 Aerodynamic characteristics with sweep angle varying |
结果表明:
(1) 从升力系数随后掠角变化曲线来看,在后掠角的整个变化过程中,非定常计算得到的升力系数均高于定常计算得到的升力系数。升力系数随后掠角的增大而减小,变后掠周期越小,即变后掠速度越大,后掠角来回变化过程中升力系数曲线所围面积越大。各变形周期的升力系数最大差异不超过0.6%。定常计算结果与非定常计算结果的最大差异出现于T=6s、35°后掠角处,此时非定常计算结果比定常计算结果大0.78%。
(2) 观察阻力系数随后掠角变化曲线可以看出,非定常计算的阻力系数随后掠角增加而增大。进一步研究发现,后掠角增大阻力实际上在减小,阻力系数增大的原因是由于变后掠过程参考面积减小引起的。非定常计算得到的阻力系数要高于定常计算得到的阻力系数,且这种差异随后掠角的增加而增大。变后掠速度越快,后掠角来回变化过程中阻力系数曲线所围面积越大。不同变后掠速度的差异不超过0.7%。去程后掠角27.5°、T=6s时,非定常计算结果与定常计算结果相差最大,此时非定常计算结果比定常计算结果大6.9%。
(3) 从俯仰力矩系数随后掠角变化曲线可以看出,俯仰力矩系数随后掠角增大而减小。不同变后掠周期得到的俯仰力矩系数随后掠角变化曲线基本没有差异,说明变后掠周期对于俯仰力矩系数的影响很小。非定常计算结果与定常计算结果的差异同样很小,两者相差最大处为T=6s、去程27.5°后掠角,此时定常计算结果比非定常计算结果大0.88%。
从之前的分析可以看出,非定常与定常气动特性的计算值有一定的差异,升力、阻力和俯仰力矩系数最大相差位置有所不同,升力系数的最大差异出现于T=6s、35°后掠角处,阻力系数与俯仰力矩系数的最大差异均出现于T=6s、去程27.5°后掠角位置。总体来看,非定常与定常气动特性相差最大不超过7%,说明在工程上可以近似采用定常气动力计算结果来代替非定常结果进行小攻角状态的初步设计,这将大大缩短设计、研制周期。
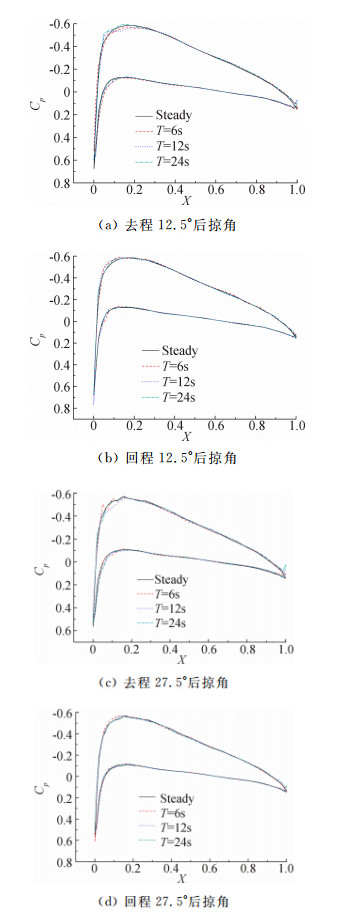
为进一步研究定常、非定常气动特性的差异,选取机翼展向2/3位置截面在去程、回程,12.5°、27.5°后掠角时,定常与非定常压力系数的计算值进行比较。为便于对比,对于机翼展向2/3位置截面的翼型长度进行归一化处理,两种后掠角的压力系数计算结果如图 5所示,可以看出:
 |
| 图 5 机翼展向位置截面压力系数Fig. 5 Pressure coefficient of wing spanwise middle position section |
(1) 两种后掠角的去、回程过程,机翼展向中间位置截面的定常、非定常压力系数计算值相差不大,定常、非定常压力系数的差异主要集中在前缘位置和后缘位置,定常压力系数所围面积较非定常小,这是定常升力系数小于非定常升力系数的原因;
(2) 随后掠角增大,定常计算结果与非定常计算结果的差异有所增大,在前、后缘与机翼上、下表面5%~40%弦长位置,这种变化比较明显;
(3) 后掠角增大,机翼展向中间位置截面压力系数曲线所围面积减小,说明后掠角增大,此截面的升力降低。图 4的分析中同样说明了这点,即后掠角增加升力系数减小。
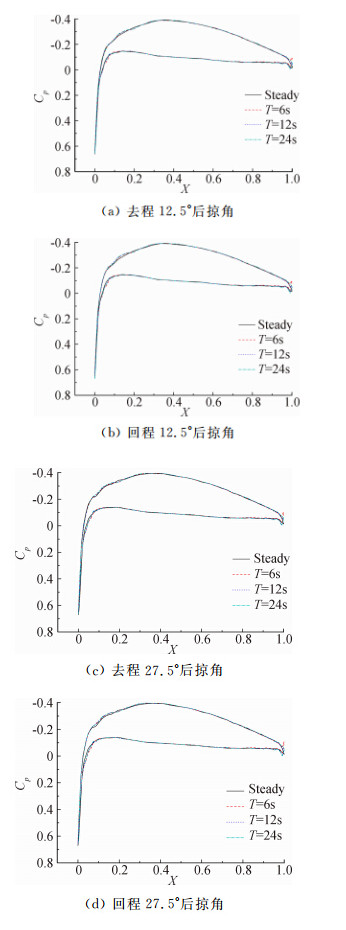
由之前的分析可以看出,定常、非定常气动力的差异在一定程度上是由机翼上压力系数的差异造成的。同样的气动力差异是否也存在于平尾上?为了研究这一问题,选取距机身对称面0.31m处的平尾截面,比较去程、回程,12.5°、27.5°后掠角时,定常与非定常压力系数的计算结果。同样为便于比较,对于平尾截面的翼型长度进行归一化处理,三种后掠角的压力系数计算结果如图 6所示,可以看出:
 |
| 图 6 平尾截面处的压力系数Fig. 6 Pressure coefficient of horizontal tail section |
(1) 虽然采用了相同的翼型,但由于受到机翼扰流的干扰,不同后掠角去、回程平尾截面处的压力系数均呈现出不同于机翼的结果,具体表现在平尾截面前缘上、下表面的压差更小,靠近后缘位置压力系数更为“开阔”,上、下表面的逆压梯度相对于机翼2/3位置截面更小。这样的压力分布有助于延缓气流分离的发生;
(2) 不同后掠角的定常计算结果与非定常计算结果相差不大,只有在回程12.5°、27.5°后掠角时稍有差异,但这种差异较小,可以忽略,即认为不同后掠角变化周期对于平尾截面上的气动力影响不大;
(3) 随后掠角的增大,平尾截面上压力系数分布几乎没有变化,即不同后掠角时平尾截面上的升力没有改变,这说明不同后掠角时变后掠飞行器升力系数的变化主要由机翼上的气动力变化引起。
通过以上分析可知,变后掠飞行器的定常与非定常气动特性存在一定的差异,但这种差异较小,且主要是由于机翼上的气动力变化造成的,平尾对于气动特性差异的贡献不大。 3.3 气动特性差异机理分析
造成定常、非定常气动特性差异的原因,可能有两个:一是流场结构的迟滞,二是机翼附加速度。下面将对这两个原因分别进行分析。 3.3.1 流场结构迟滞
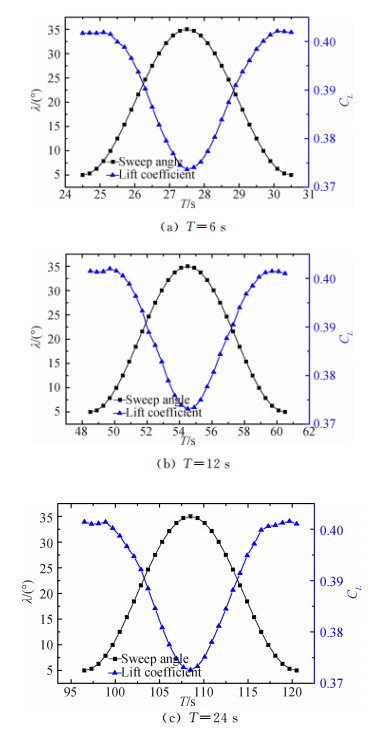
图 7中呈现了三种变后掠周期的升力系数和后掠角随时间变化的趋势。可以看出:三种变后掠周期的升力系数均随后掠角同步变化。后掠角变大,升力系数降低;后掠角变小,升力系数增加。后掠角的峰值出现时刻与升力系数峰值出现时刻相同。
如果存在流场结构的迟滞,那么升力系数的变化一定会滞后于后掠角的变化。而图 7中呈现的结果 排除了流场结构迟滞造成定常、非定常气动特性差异的可能性,说明不存在流场结构迟滞。
 |
| 图 7 后掠角与升力系数随时间的变化Fig. 7 Variation of sweep-angle and lift coefficient with time |
选用T=6s变后掠周期,27.5°后掠角的去、回程进行分析。图 8中呈现了距机身对称面1.3m机翼截面处的定常与非定常压力系数云图。可以看出: 27.5°后掠角时,定常与去程非定常计算结果在前缘部位和截面上下表面1/4弦长位置有所不同。定常计算结果在前缘位置的压力系数最大值范围较去程非定常计算结果小,定常结果下表面负压区范围比去程非定常结果更大,所以去程非定常阻力、升力比定常升力计算值偏大。
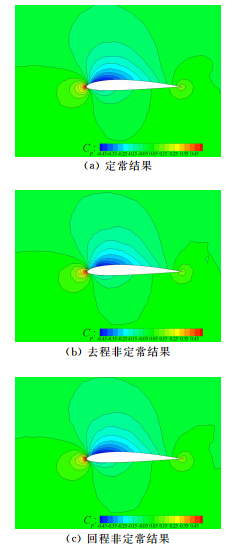 |
| 图 8 27.5°时机翼截面压力系数云图Fig. 8 Wing-sectional pressure coefficient contour for 27.5° sweep angle |
回程非定常计算结果与定常计算结果同样在前 缘部位和截面上下表面1/4弦长位置不同。定常计算结果在前缘位置的压力系数最大值范围较回程非定常计算结果小,定常结果下表面负压区范围比回程 非定常结果小,但回程非定常结果上表面负压区范围较定常结果大,总的作用结果为回程非定常阻力、升力比定常升力计算值偏大。
由此说明机翼的附加速度可能是引起定常、非定常气动特性差异产生的原因。且由之前的分析可知机翼相对气流的运动速度越快,即变后掠周期越短,定常与非定常计算结果的差异越大。 4 结 论
(1) 对于给定的后掠角,柔性变后掠飞行器的升力、阻力系数随攻角增大而增加,俯仰力矩系数随攻角增大而减小,升阻比随攻角先增大后减小;总体上看,攻角小于14°时,小后掠可以取得较大的升力、阻力系数,大于14°攻角,大后掠的升力、阻力系数较大;增加后掠角可以增强飞行器的稳定性;所有后掠角均在4°攻角处取得最大升阻比且小后掠角的升阻比较大;当升力系数小于1.28时,小后掠角产生较小的阻力系数,超过这一数值,大后掠角的阻力系数较小。
(2) 非定常计算的升力、阻力系数大于定常结果,俯仰力矩系数与定常计算值差异不大,三种气动力最大差异出现时对应的状态不同;在攻角小于2°的情况下,非定常与定常气动特性最大差异不超过7%;非定常与定常气动力的差异主要由变后掠过程中机翼上的气动力差异引起,平尾的影响不大。
(3) 变后掠过程中定常与非定常气动特性的差异可能是由于机翼的附加速度引起的,与流场迟滞无关,且机翼相对于气流的运动速度越快,两者的差异越大。
| [1] | Jha A K, Kudva J N. Morphing aircraft concepts, classifications, and challenges[C]//AndersonE H. Smart Structures and Materials 2004: Industrial and Commercial Applications of Smart Structures Technologies. Bellingham: SPIE, 2004: 213-224. |
| [2] | Bowman J C, Plumley R W, Dubois J A, et al. Mission effectiveness comparisons of morphing and non-morphing vehicles[R]. AIAA 2006-7771, 2006. |
| [3] | Smith K, Butt J, Von Spakovsky M R. A study of the benefits of using morphing wing technology in fighter aircraft systems[R]. AIAA 2007-4616, 2007. |
| [4] | Hassan A A, Osborne B, Schwimley S, et al. Control of shock-boundary layer interactions (SBLIs) using an oscillatory jet[R]. AIAA 2007-476, 2007. |
| [5] | Raju R, Mittal R, Cattafesta L. Dynamics of airfoil separation control using zero-net mass-flux forcing[J]. AIAA Journal, 2008, 46(12): 3103-3115. |
| [6] | Zhang S Y, Zhong S. An experimental investigation of flow separation control sing an array of synthetic jets[R]. AIAA 2009-4185, 2009. |
| [7] | Duan H S, Liu P Q, He Y W, et al. Numerical investigation of drag-reduction control by micro-suction-blowing on airfoil[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(7): 1219-1226. (in Chinses) 段会申, 刘沛清, 何雨薇, 等. 二维翼型微吸吹气减阻控制新技术数值研究[J]. 航空学报, 2009, 30(7): 1219-1226. |
| [8] | West IV T K, Hosder S. Numerical investigation of plasma actuator configurations for flow separation control at multiple angles of attack[R]. AIAA 2012-3053, 2012. |
| [9] | Rodriguez A R. Morphing aircraft technology Survey[R]. AIAA 2007-1258, 2007. |
| [10] | Ivanco T G, Scott R C, Love M H, et al. Validation of the lockheed martin morphing concept with wind tunnel testing[R]. AIAA 2007-2235, 2007. |
| [11] | Flanagan J S, Strutzenberg R C, Myers R B, et al. Development and flight testing of a morphing aircraft, the next gen MFX-1[R]. AIAA 2007-1707, 2007. |
| [12] | Hall J M. Executive summary AFTI/F-111 mission adaptive wing[R]. WRDC-TR-89-3083, 1989. |
| [13] | Kudva J. Overview of the DARPA smart wing project[J]. Journal of Intelligent Material System and Structure, 2004, 15: 261-267. |
| [14] | Bowman J, Sanders M B, Weisshaar D T. Evaluating the impact of morphing technologies on aircraft performance[R]. AIAA 2002-1631, 2002. |
| [15] | Neal D A, Good M G, Johnston C O, et al. Design and wind-tunnel analysis of a fully adaptive aircraft configuration[R]. AIAA 2004-1727, 2004. |
| [16] | Love M H, Zink P S, Stroud R L, et al. Demonstration of morphing technology through ground and wind tunnel tests[R]. AIAA 2007-1729, 2007. |
| [17] | Chen Qian, Bai Peng, Chen Nong, et al. Investigation on the unsteady aerodynamic characteristics of sliding-skin variable-sweep morphing unmanned aerial vehicle[J]. Acta Aerodynamica Sinica, 2011, 29(5): 645-650. (in Chinese) 陈钱, 白鹏, 陈农, 等. 滑动蒙皮变后掠无人机非定常气动特性研究[J]. 空气动力学学报, 2011, 29(5): 645-650. |
| [18] | Thomas P D, Lombard C K. The geometric conservation law-a link between finite-difference and finite-volume methods of flow computation on moving grids[R]. AIAA 78-1208, 1978. |
| [19] | Ostowari C, Naik D. Post-stall wind tunnel data for NACA 44XX series airfoil sections[R]. SERI/STR-217-2559, 1985. |
| [20] | Landon R H, A R A. Compendium of unsteady aerodynamic measurements[R]. AGARD 0-R-702, 1982. |