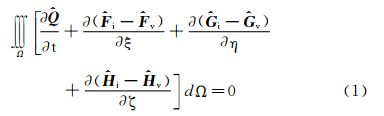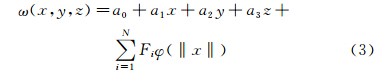2. 中国航空工业第一飞机设计研究院, 陕西 西安 710072
2. AVIC, The First Aircraft Institute, Xi'an Shaanxi 710072, China
0 引 言
翼吊发动机由于其特殊的优点,在现代民用飞机布局中被广泛采用[1]。在民用飞机的设计中,需要大展弦比机翼在跨声速进行巡航。大展弦比机翼的刚度普遍比较小,机翼的气动弹性变形比较严重,从而极大地影响了飞机的飞行性能[2, 3, 4]。并且,对大展弦比机翼进行气动弹性分析的时候必须考虑大位移小应变效应,即结构非线性问题[4]。翼吊涡扇发动机布局又会对机翼的气动弹性变形产生新的影响。动力条件发动机的进排气会对机翼/短舱/挂架产生干扰,从而导致组合体气动载荷的显著变化,引起静气动弹性效应的改变。
从20世纪80年代开始,国外就对发动机的进排气进行了研究。Hirose N[5],Deese J[6]等人通过数值求解欧拉方程,模拟了发动机的进排气效应,得到了进排气效应引起唇口激波强度变化的结论。在国内,张美红[7]等采用CFX软件,应用N-S方程对发动机喷流影响进行了初步探讨。谭兆光[8, 9]等通过设置边界条件来模拟发动机的喷流效应,并与试验值进行对比,主要是为了确定N-S方程用于动力计算的可行性。李强[10]等研究了动力体和组合体的干扰,表明涡流流动在干扰区内对短舱-挂架-机翼结构的各种气动特性产生较大的干扰,其大小、分布位置及面积成为决定短舱及机翼气动特性的一个重要因素。
对于静气动弹性分析,J R Wright[11]指出结构模型已从基于有限元(FE)方法的“梁式”模型发展到更具有代表性的“盒式”有限元模型。刘东岳[12]等将“梁式”有限元模型和“盒式”有限元模型进行了对比分析,盒式有限元模型基于刘成玉[13]等的简化方法进行简化,表明三维盒式有限元模型得到的刚度分布更接近于实际情况,适于静气动弹性分析。C B Allen等[14, 15, 16, 17]发展了一种基于RBF的插值技术和动网格方法,可以准确地进行流固耦合数据的交换并有很强的动网格变形能力。此外,NASA在National Transonic Facility进行了一系列的DLR-F6构型的静气动弹性风洞试验[18],对比了翼身组合体(WB)/翼身组合体加整流包(WBF)/翼身组合体挂架短舱(WBPN)(通气短舱)等构型定升力系数下后缘的挠度分布和顺气流剖面的扭转角分布。Stefan K[19]发展了一种静气动弹性分析方法,对DLR-F6构型(含挂架和通气短舱)进行了静气动弹性计算,并进行了算例验证,表明了该方法的可信性。
但是对于考虑喷流影响的民用客机的静气动弹性分析,在国内外公开发表的文献中鲜有研究,而发动机的喷流效应对机翼表面的载荷分布又有很大影响。因此,本文针对多块结构网格,开展了一种基于RBF插值技术的数据交换方法和RBF&Delaunay多块结构动网格方法,并通过耦合基于多块结构网格的N-S方程求解器和结构柔度矩阵方法,发展了静气动弹性分析方法,并用DLR F6模型[18]对此方法进行验证。在此基础上对比分析了无喷流/有喷流的全机构型,得到了无喷流/有喷流构型弹性机翼的真实载荷和几何变形,分析了喷流效应对机翼静气动弹性变形的影响。 1 CFD计算方法 1.1 CFD控制方程
静气动弹性主要是研究飞机跨声速飞行时气动力与弹性力的耦合问题,为了准确地捕捉飞机跨声速飞行时的间断如激波和滑移面,本文通过定常的RANS方程对其进行数值模拟。其积分形式的主控方程为[20]:
采用有限体积法求解该方程,空间离散格式为二阶迎风Roe格式,时间推进为四步龙格-库塔方法,引入k-ω SST湍流模型,在计算空间生成多块结构网格,为了提高计算效率,采用多机多核并行计算并引入多重网格加速收敛算法。 1.2 发动机喷流边界条件及验证
边界条件包括远场、对称面和无滑移壁面边界条件,发动机进气和排气的边界条件。
运用CFD来模拟发动机喷流对全机气动力影响,主要是通过设置边界条件来实现,主要包括风扇入口边界条件和外涵道、核心机出口边界条件。积分力时未考虑发动机的推力,只计及了喷流效应的影响。
进气条件:进气口作为计算域的出口,为亚声速。根据特征线理论,亚声速出流边界只需指定一个参数,其他变量由流场内部向外插值得到。计算中在发动机风扇入口给定静压,以模拟发动的进气作用。
排气条件:排气口是计算域的入口,通常也是亚声速。根据特征线理论,亚声速入流边界需指定四个参数,另外一个变量由流场内部向外插值得到。在此处给定发动机流动方向垂直于表面(即两个限制条件),并给定外涵道出口和核心机出口的总温总压边界条件,以模拟高速喷流。
采用某型涡扇发动机(图 1)对模拟发动机喷流所采用数值方法的可靠性进行验证。数值模拟中Ma=0.2,高度为海平面标准大气。图 2(a)、图 2(b)分别为沿发动机中轴线喷流总温、静温随距离变化的数值模拟结果与试验值的对比。从图 2中可以看出,在距核心机后缘端面最近及最远处计算值和试验值符合最好,在中等距离处计算值与试验值存在小的差异,但误差范围不超过10%。该算例表明本文针对发动机喷流模型所采用的数值模拟方法可以满足本文研究工作的需求。
 |
| 图 1 某发动机模型Fig. 1 Geometries of nacelle |
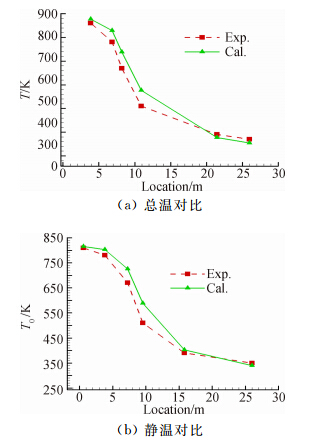 |
| 图 2 计算值与试验值的对比Fig. 2 Comparison of experiment and calculation |
采用MSC PATRAN对机翼/挂架/发动机进行有限元建模,全机有喷流构型的三维有限元模型如图 3所示。根据机翼各部分的承力特性,采用板杆结构来模拟机翼:上下蒙皮、翼肋、前后梁腹板及发动机均用板单元模拟,上下长桁及前后梁缘条均采用杆单元模拟,不同材料及各部件的转换关系参照文献[13]。
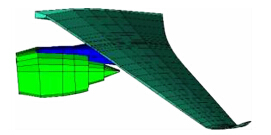 |
| 图 3 三维有限元模型Fig. 3 Three-dimensional finite element model |
采用柔度矩阵方法求解结构静力学方程。仅考虑飞机机翼的弹性变形,其他部件如发动机及挂架等都视为刚性部件,但发动机和挂架视为与机翼弹性变形随动。其结构静力学方程如下:
式中: q s为结构点在三个方向的变形位移矩阵; C为结构柔度矩阵;F s为作用在节点上的气动力矩阵; G s为结构质量矩阵; P s发动机推力矩阵。 3 静气动弹性分析方法 3.1 三维径向基函数插值方法CFD模型是基于N-S方程描述的,结构模型是基于拉格朗日方程描述的。气动模型和结构模型的建模方式大不相同,不论是把流场表面网格点上的力传递到结构模型,还是把结构模型的位移转化为流场边界的位移,都需要进行数据的传递,CFD/CSD数据传递满足虚功原理。本文采用三维径向基函数(RBF)[14, 15]进行结构和气动数据的交换,其插值公式为:
式中:径向基函数的选取比较自由,本文选取φ(‖x‖)=(1-‖x‖)2。以位移插值为例,只要确定式(3)中的N+4个未知数a0,a1,a2,a3,F1,F2,…,FN,就可以确定数据转换矩阵。 3.2 多块网格动网格技术
在进行静气动弹性分析时,如何通过结构求解获得的变形信息迅速实现气动网格更新是一项关键技术。本文采用了一种RBF&Delaunay[14]动网格方法。这种方法集成了RBF适用于大变形问题的特点和Delaunay方法变形迅速的特点。该动网格方法只需要计算Nblock points×Nsurface points(N矩阵维数,下标block points代表结构网格块的顶点,下标surface points代表表面网格点)的变换矩阵。每个结构网格块内网格根据顶点网格并应用Delaunay方法进行变换,得到新的气动网格[16]。
值得注意的是,网格变形和CFD/CSD数据交换需要满足的要求是不同的,CFD/CSD数据变换矩阵需要保证准确的力和力矩平衡准则而包含线性项,而网格变换矩阵为了避免边界网格的移动和非物理力的传递而不需要线性项。所以要分别建立CFD/CSD数据变换矩阵和动网格变换矩阵[15, 16, 17]:
式中:L为动网格变换矩阵(X代表网格块顶点坐标,下标mesh代表网格块顶点,下标a代表表面网格点)。 3.3 静气动弹性分析流程静气动弹性分析是气动力模型和结构模型不断耦合、不断交换数据的过程,当两者均达到收敛时,得到一个最终的静气动弹性分析结果。本文采用RBF数据交换技术进行气动数据和结构数据之间的交换,并采用RBF&Delaunay动网格技术,开展了一种适用于大展弦比飞机静气动弹性分析的方法。其流程如图 4所示。
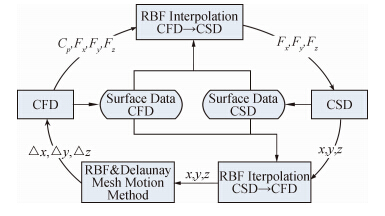 |
| 图 4 静气动弹性分析流程图Fig. 4 Flow chart of the static aeroelasticity analysis |
本文采用DLR F6翼身组合体构型进行非线性气动弹性分析程序的验证。该算例被许多研究者采用。采用定常RANS方程求解流场,在每一步耦合非线性静力学分析。本算例的计算状态为:Ma= 0.75,Re=3×106,定升力系数CL=0.5。机翼采用翼盒结构,采用实体模拟机翼,并挖空其中的中央翼盒部分。材料的弹性模量E=2.05×1011,泊松比v=0.3。
图 5是DLF F6结构变形云图。可以看出,机翼的弹性变形主要表现为弯曲变形和较小的低头扭转变形,这是典型的后掠机翼的静气动弹性现象。从图 5中可以看出,机翼内翼段变形量很小,沿展向变形量逐渐增大,并在翼尖达到最大值。由于弹性变形的影响,机翼沿流向各个剖面产生负的扭转角,并沿展向逐渐增加,在翼尖达到最大值。图 6是后缘挠度收敛曲线,计算在五步就达到了收敛,变形量残差ε≤1×10-5。图 7(a)、图 7(b)分别是后缘挠度与展向扭转角分布和试验值[18]的对比图。由图 7可知,该方法对后缘挠度和展向扭转角分布捕捉都比较准确,五个典型站位的后缘挠度和展向扭转角都和试验值吻合得比较好,95%展向位置的挠度与试验值相差6.6%,95%的扭转角与试验值相差3.7%,表明本文的静气动弹性分析方法是可信的。
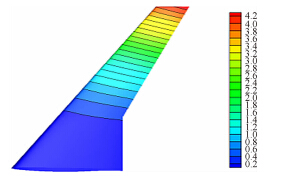 |
| 图 5 结构变形云图Fig. 5 Contour of structure deformation |
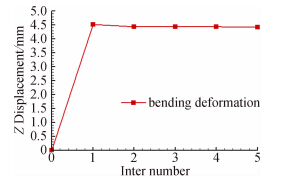 |
| 图 6 后缘挠度收敛曲线Fig. 6 Convergence course of tailing edge bending deformation |
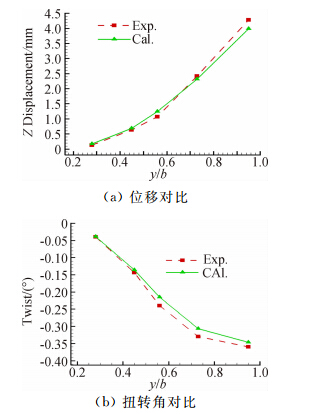 |
| 图 7 计算值与试验值的对比Fig. 7 Comparison of experiment and computation |
前文应用本文的静气动弹性分析方法对DRL F6翼身组合体构型进行了验证,下面应用该方法对某型民用飞机无喷流/有喷流构型进行静气动弹性分析,并对分析结果进行对比。 4.1 计算模型
图 8是无喷流/有喷流构型对比图。展长为17.204m,展弦比为8.087。计算状态为:Ma=0.785,基于单位弦长的无量纲化雷诺数Re=5.8×106,α=2.4°。机翼采用双梁单块式结构,材料为铝合金,弹性模量为E=70GPa,泊松比μ=0.3。机翼由前后梁、上下壁板和翼肋组成,上下壁板为蒙皮/长桁加强筋结构,梁采用整体结构。本算例考虑了发动机及发动机喷流对气动力的影响,在弹性结构有限元分析时把发动机和机身视为刚性的,只考虑机翼的弹性变形。
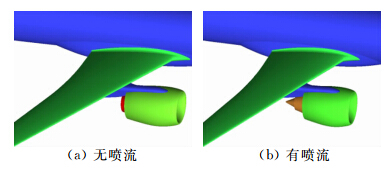 |
| 图 8 无喷流/有喷流构型Fig. 8 No jet/jet configuration |
图 9给出了无喷流/有喷流构型的气动网格对比图。为保证计算结果的可信度,气动网格采用实体空化网格策略。首先生成全机有喷流构型的多块结构网格,再把短舱部分多余的网格空化为流场,生成全机无喷流构型的网格。这样,两构型除了短舱不同部分所占据的空间,其他空间部分的网格均一样,保证了气动求解结果的可比性。
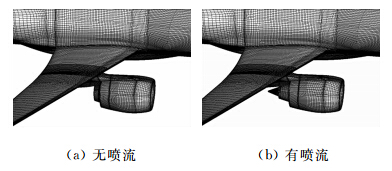 |
| 图 9 无喷流/有喷流构型网格图Fig. 9 No jet/jet configuration mesh |
同时,三维结构有限元模型(图 10)也进行空化处理。首先生成全机有喷流构型的结构表面网格,再把短舱部分的网格进行处理,生成无喷流全机的结构网格,并给两构型同样的材料属性,这样,两构型除了短舱部分的网格,其他部分网格,结构布置均保持一致,保证了结构求解结果的可比度。
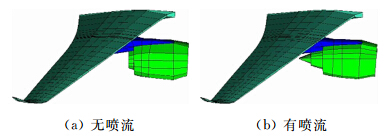 |
| 图 10 三维有限元模型Fig. 10 Three-dimensional finite element model |
对于刚性机翼,喷流对上下翼面的压力分布影响均很大。图 11(a)、12(a)给出了喷流前后刚性机翼上翼面的压力云图对比,图 11(c)、12(c)给出了喷流前后下翼面的压力云图对比。可以看出:喷流后上翼面的激波变强;下翼面无喷流构型在内翼段与机翼间存在低速区,喷流后喷口和机翼间存在激波,原始构型的低速区变成高速区,内翼段下翼面最大速度增加,升力损失。在4.4节中对刚性机翼与弹性机翼的结果进行了详细对比。
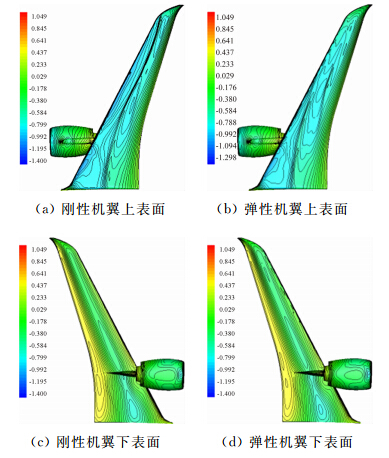 |
| 图 11 无喷流构型弹性变形前后的压力云图对比Fig. 11 Comparison of pressure coefficient contour of no jet configuration |
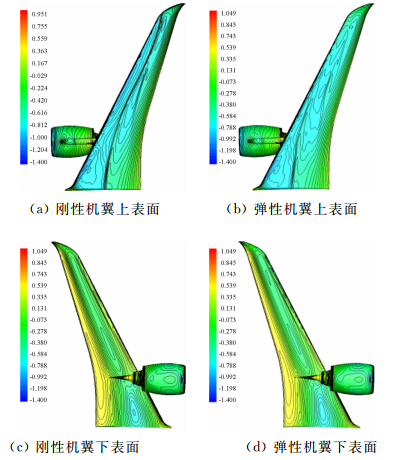 |
| 图 12 有喷流构型弹性变形前后的压力云图对比Fig. 12 Comparison of pressure coefficient contour of jet configuration |
图 13中的红色带方形线和蓝色带左三角线给出了喷流前后刚性机翼四个截面中压力分布对比。喷流使发动机喷流区的上表面激波前移,压力峰值降低,并影响到外翼段,在距离对称面10m外压力峰值恢复到无喷流水平。喷流后,下翼面发动机喷流区速度提高,压力峰值增高,升力损失。
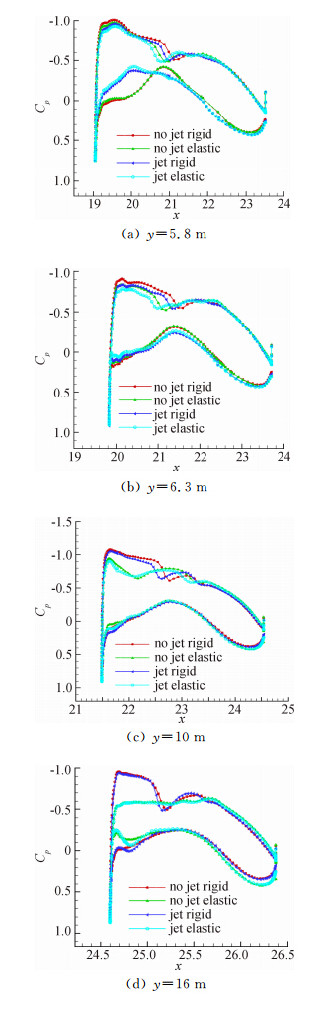 |
| 图 13 无喷流/有喷流构型变形前后机翼剖面压力分布对比Fig. 13 Comparison of pressure coefficient distribution of no jet /jet configuration |
图 14给出了考虑机翼弹性变形前后的无喷流/有喷流构型的结构变形云图对比。两构型机翼的弹 性变形均引起机翼向上的挠度,同时在机翼顺气流剖面产生负的扭转角,使机翼沿展向各剖面的迎角减小。机翼的内翼段变形量很小,沿展向变形量逐渐增大,在翼尖达到最大值。
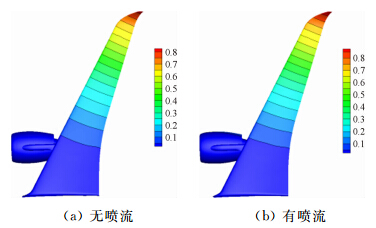 |
| 图 14 无喷流/有喷流构型位移云图Fig. 14 No jet/jet contour of structure deformation |
图 15给出两构型监测点挠度收敛曲线对比和全机升力系数收敛曲线对比。计算在七步达到收敛,变形量与升力系数残差ε≤1×10-3。
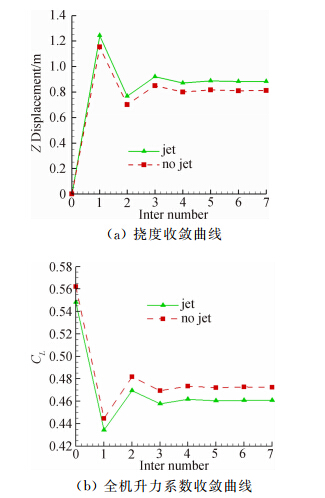 |
| 图 15 收敛曲线Fig. 15 Convergence course |
图 16、图 17给出了两构型的前后缘挠度分布和扭转角对比图。从图 14、图 16和图 17可知,两构型的同一顺气流剖面的后缘挠度均大于前缘挠度,这会导致机翼产生负的扭转角,并且沿展向扭转角越来越大,在翼尖达到最大值。
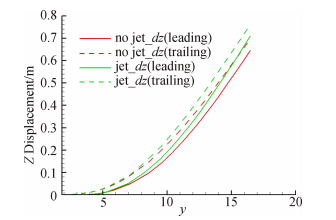 |
| 图 16 前后缘挠度对比Fig. 16 Comparison of leading/trailing edge bending de-formation |
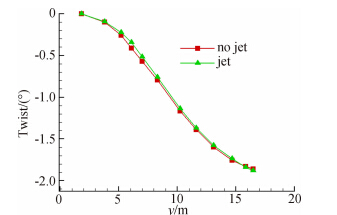 |
| 图 17 扭转角对比Fig. 17 Comparison of twist angle |
值得注意的是,有喷流构型的前后缘挠度均大于无喷流构型的(图 16),但有喷流构型弹性变形引起的多数剖面的附加扭转角小于无喷流构型(图 17,即有喷流构型当地攻角大),仅在靠近翼尖的几个站位,有喷流构型的扭转角大于无喷流构型,且越靠近发动机轴线(y=6.1m)的站位,有喷流构型与无喷流构型的扭转角差值越大。这是由于发动机喷流给全机产生了一个正的扭转效应,抵消一部分机翼后掠效应的影响,引起机翼表面载荷的重新分布。这样,考虑发动机喷流影响后,前后缘挠度均会有所增大,弹性变形引起的多数剖面的附加扭转角有所减小。
图 11(a)~(d)、图 12(a)~(d)分别为弹性变形前后无喷流/有喷流构型机翼上下表面的压力云图对比。机翼受弹性变形影响后,无喷流/有喷流构型上翼面的激波均往前缘移动,升力系数进一步损失,下翼面影响较小。机翼表面的载荷重新分布。图 13给出了有喷流/无喷流构型变形前后机翼几个典型剖面压力分布对比。对比红色方块线与绿色带正三角线(无喷流构型弹性变形前后),深蓝色带左三角线与天蓝色带圆形线(有喷流构型弹性变形前后)可知,不论是有喷流构型还是无喷流构型,机翼的静气动弹性变形对上表面压力分布影响较大,对下表面压力分布影响较小。机翼的弹性变形引起内翼段上表面激波前移,越靠近外侧剖面处影响越大,在翼尖处激波基本消失。对比红色方块线、绿色带正三角线与天蓝色带圆形线可知,考虑喷流影响的机翼静气动弹性效应是一种耦合效应,发动机喷流区主要受到喷流影响,弹性变形影响较小,上表面激波前移,下表面压力峰值增加;而机翼外翼段又主要受弹性变形影响,喷流影响较小,上表面激波前移;正是这种耦合作用,构成了考虑喷流影响的机翼静气动弹性效应,上表面激波大量前移,下表面压力峰值增加。
为了进一步说明静气动弹性和喷流的影响区域,图 18给出了弹性变形前后无喷流/有喷流构型机翼剖面展向升力系数对比图。对比红色方块线与深蓝色带下三角线(刚性机翼喷流前后),绿色带正三角线与天蓝色带右三角(弹性机翼喷流前后)可知,喷流影响作用在机翼的内翼段,引起升力的损失。分析对比刚性机翼喷流前后及弹性机翼喷流前后展向升力系数的差量可知,弹性变形前,无喷流构型外翼段大多数剖面的升力系数大于有喷流构型,而弹性变形后,由于有喷流构型大多数剖面的当地攻角大于无喷流构型(图 17),有喷流构外翼段的升力系数增加,大多数剖面的升力系数均高于无喷流构型。喷流主要影响机翼的内翼段(约为y<8m),发动机区域(y≈4.7m~7.5m)影响最大;弹性变形主要影响机翼的外翼段(约为y=8m~19m),机翼受影响的区域较大。
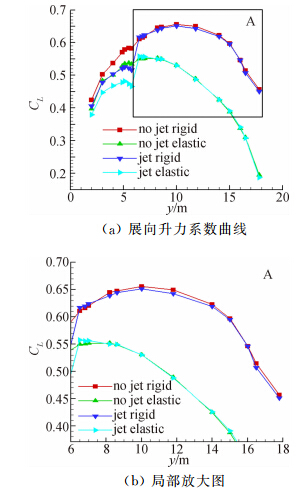 |
| 图 18 机翼剖面展向升力系数曲线对比Fig. 18 Comparison of lift coefficient distribution of wingspan |
由本算例可知,弹性变形对机翼的气动性能产生了重要影响,发动机喷流效应又会使气动性能进一步改变。表 1给出了弹性变形前后无喷流/有喷流构型的力系数对比。由表 1可知:无喷流影响时机翼的弹性变形使升力系数下降约16%,升阻比下降8.4%;计及喷流影响时,升力系数下降达到18%,升阻比下降36%。因此,对于大展弦比机翼考虑喷流影响的静气动弹性分析十分必要。
| CL | CD | CL/CD | |
| rigid wing(no jet) | 0.5621 | 0.02907 | 19.336 |
| rigid wing(jet) | 0.5480 | 0.03959 | 13.841 |
| elastic wing(no jet) | 0.4725 | 0.02668 | 17.710 |
| elastic wing(jet) | 0.4606 | 0.03724 | 12.368 |
(1) 采用的静气动弹性分析方法充分考虑了大展弦比机翼结构求解和气动求解的非线性问题,采用DLR F6翼身组合体构型进行了验证,计算值与试验值吻合良好,表明本文采用的静气动弹性分析方法是可信的。
(2) 对于刚性机翼,喷流会使上翼面发动机喷流区激波增强,压力峰值降低,并影响到外翼段。喷流后,下翼面发动机喷流区速度提高,压力峰值增高,升力损失。
(3) 对于弹性机翼,发动机喷流会给机翼带来一个正的扭转效应,抵消一部分机翼后掠效应的影响,使机翼前后缘挠度均会有所增大,弹性变形引起的多数剖面的附加扭转角减小。
(4) 考虑喷流的机翼静气动弹性变形是一个耦合效应,发动机喷流区主要受喷流影响,外翼段主要受弹性变形影响。无喷流影响时机翼的弹性变形使升力系数下降约16%,升阻比下降8.4%,计及喷流影响是,升力系数下降达到18%,升阻比下降36%。对于大展弦比机翼考虑喷流影响的静气动弹性分析十分必要。
| [1] | Dang T H. The engine installation of civil aircraft with wing mounted engine configuration[J].Civil Aircraft Design and Research, 2008, (2): 8-14. (in Chinese) 党铁红. 翼吊布局民用飞机发动机安装设计[J]. 民用飞机设计与研究, 2008, (2): 8-14. doi: 10.3969/j.issn.1674-9804.2008.02.003 |
| [2] | Fuxin H W. The principle of aeroelastic mechanics[M]. Shen K Y, Guan D, translated. Shanghai: Shanghai Science and Technology Document Aviation Industry Press, 1998: 24-27. (in Chinese) H W伏欣. 气动弹性力学原理[M]. 沈克扬, 管德, 译. 上海: 上海科学技术文献出版社, 1982: 24-27. [3] Chen G B, Zhou C Q, Yang C. Aeroelastic design basis[M]. Beijing: Beihang University Press, 2004. (in Chinese) 陈桂宾, 邹从青, 杨超. 气动弹性设计基础[M]. 北京: 北京航空航天大学出版社, 2004. |
| [4] | Ye Z Y, Zhang W W, Shi A M, et al. Fundamentals of fluid-structure coupling and its application[M]. Harbin: Harbin Institute of Technolody University Press, 2010. (in Chinese) 叶正寅, 张伟伟, 史爱明, 等. 流固耦合力学基础及其应用[M]. 哈尔滨: 哈尔滨工业大学出版社, 2010. |
| [5] | Hirose N, Asai K. 3-D Euler flow analysis of fanjet engine and turbine powered simulator with experimental comparison in transonic speed[R]. AIAA 89-1835, 1989. doi: 10.2514/6.1989-1835, 10.2514/MFDC89 |
| [6] | Deese J E, Agarwal R K. Calculation of axisymmetric inlet flow field using the Euler equations[R]. AIAA 83-1853, 1983. doi: 10. 2514/6.1983-1853, 10. 2514/MAAC83 |
| [7] | Zhang M H, Wang Z D. The application of CFD in powered aircraft aerodynamic design[J]. Civil Aircraft Design and Research, 2004, (4): 52-55. (in Chinese) 张美红, 王志栋. CFD技术在喷流飞机气动设计中的应用[J]. 民用飞机设计与研究, 2004, (4): 52-55. doi: 10.3969/j.issn.1674-9804.2004.04.011 |
| [8] | Tan Z G, Chen Y CH, Li J, et al, Numerical simulation method for the powered effectsin airframe/propulsion integration analysis[J]. Journal of Aerospace Power, 2009, 24(8): 1766-1772. (in Chinese) 谭兆光, 陈迎春, 李杰, 等. 机体/动力装置一体化分析中的动力影响效应数值模拟[J]. 航空动力学报, 2009, 24(8): 1766-1772. |
| [9] | Jia H Y, Deng Y Q, Ma M S, et al, Numerical investigation of the powered effects on civil aircraft[J]. Acta Aerodynamica Sinica, 2012, 30(6): 725-730. (in Chinese) 贾洪印, 邓有奇, 马明生, 等. 民用大飞机动力影响数值模拟研究[J]. 空气动力学学报, 2012, 30(6): 725-730. |
| [10] | Li Q, Wang M S. Numerical simulation of wing/nacelle/pylon aerodynamic characteristics and their changes under powered condition[J]. Journal of Aerospace Power, 2012, 27(7): 1588-1594. (in Chinese) 李强, 汪明生. 翼/短舱/吊架气动特性及其动力影响数值研究[J]. 航空动力学报, 2012, 27(7): 1588-1594. |
| [11] | Wright J R, Cooper J E. Introduction to aircraft aeroelasticity and loads[M]. Yao Y L, translated. Shanghai Jiao Tong University Press, 2010. (in Chinese) J R赖特, J E 库珀. 飞机气动弹性力学与载荷导论[M]. 姚一龙, 译. 上海交通大学出版社, 2010. |
| [12] | Liu D Y, Wan Z Q, Yang C, et al. Aeroelastic optimization design of global stiffness for high aspect ratio wing[J]. Acta Aeronoutica et Astronautica Sinica, 2011, 32(6): 1025-1031. (in Chinese) 刘东岳, 万志强, 杨超, 等. 大展弦比机翼总体刚度的气动弹性优化设计[J]. 航空学报, 2011, 32(6): 1025-1031. doi: 11-1929/V.20110106.1117.000 |
| [13] | Liu C Y, Huang G L, Wang L J. Computation of stiffness characteristic of a high aspect ratio wing[J]. Aircraft Project, 2006, (4): 21-24. (in Chinese) 刘成玉, 黄国宁, 王利京. 某大展弦比机翼的刚度特性计算[J]. 飞机工程, 2006, (4): 21-24. |
| [14] | Buhmann M. Radial Basis Functions[M], Cambridge: Cambridge University Press, 2005. |
| [15] | Allen C B, Rendall T C S. Unified approach to CFD-CSD interpolation and mesh motion using Radial Basis Functions[R]. AIAA 2007-3804. doi: 10.2514/6.2007-3804, 10.2514/MAAC07 |
| [16] | Ahrem R, Beckert A, Wendland H. A meshless spatial coupling schemefor large-scale fluid-structure-interaction[J]. Tech. Science Press, 2006, 12(2): 121-136. |
| [17] | Jakobsson S, Amoignon O. Mesh deformation using radial basis functions for gradient based aerodynamic shape optimization[R]. FOI-R-1784-SE, FOI, 2005. doi: S0045793006001320 |
| [18] | Alpheus W Burner, William K Goad, Edward A Massey. Wing deformation measurements of the DLR-F6 transport configuration in the National Transonic Facility[R]. AIAA 2008-6921, 2008. doi: 10.2514/6.2008-6921, 10.2514/MAAC08 |
| [19] | Stefan K, Ralf R. Aero-Elastic simulation of DLR's F6 transport aircraft configuration and comparison to experiment data[R]. AIAA 2009-580, 2009. doi: 10.2514/6.2009-580, 10.2514/MASM09 |
| [20] | John D Anderson. Computational fluid dynamics[M]. WU S P, Liu Z M, translated. Shanghai: China Machine Press, 2007. (in Chinese) 约翰 D 安德森. 计算流体力学基础及其应用[M]. 吴颂平, 刘赵淼, 译. 机械工业出版社, 2007. |