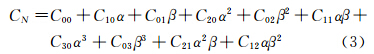0 引 言
风洞试验是飞行器空气动力特性研究的主要手段之一,在方案初选、设计优化和定型等研制阶段,需要进行大量的风洞试验,为总体、控制和结构等专业提供设计依据。随着我国航空航天事业的发展,各类飞行器设计的技术指标日益提高,对空气动力风洞试验技术也提出了更高的要求。如何提高试验数据精准度、降低成本和缩短试验周期成为重要的研究方向。
风洞试验通常通过改变某些自变量,对描述气动特性的响应变量进行测量,以定量的获取二者之间的规律。其中自变量是模型姿态角、舵偏角和来流条件等,响应变量是作用在模型上的气动力和力矩、表面压力或温度分布等。传统的试验方法通常为单变量试验法,即在一次试验中选择一个自变量(如攻角)进行改变,并保持其它自变量不变,通过测量响应变量(如六分量气动力和力矩)来得到自变量和响应变量的关系。单变量法简称为OFAT(One Factor at A Time)方法。这种方法容易受试验中自变量的“共变效应”的影响[1, 2, 3, 4],如在进行改变攻角的试验时,侧滑角随着攻角变化也在轻微的改变(由于气动载荷导致的天平和支杆弹性变形),侧滑角的改变会导致试验数据的误差增大,但由于对其进行修正的难度和工作量都很大,所以通常只采用尽可能减小侧滑角的变化量的方式,或给出这个“不希望”的变化量的量值以供参考,无法分离“混淆”在试验数据中的共变效应。
1997年,美国航空航天局(NASA)兰利研究中心开始倡导一种新的试验方法来替代OFAT方法,这就是现代实验设计方法[5]。现代试验设计方法是基于这么一个认识:对于先进航空航天飞行器设计的精准度要求而言,像风洞这样复杂试验系统保持所有潜在共变因素不发生变化是不可能的。所以,不同于OFAT方法从一个数据点到下一个新数据点只改变一个变量(或因素)的取值(或水平)的方法,MDOE方法一次要改变多个变量(或因素)的值(或水平)。由于现代试验设计采用的方法最早在1935年R A Fisher[6, 7, 8]所著的《The Design of Experiments》[6]第一次被介绍,而传统的OFAT方法的应用可以追溯到文艺复兴时期,所以被称为现代试验设计(Modern Design of Experiments,MDOE)方法。
兰利研究中心非常重视MDOE风洞试验方法的应用。1997年进行四个项目对比了OFAT方法和MDOE方法的收获和成本,验证了MDOE方法在提高数据精准度[9]、降低成本和缩短周期方面的潜力[1, 10]。2001年在兰利统一规划风洞(UPWT)的发展报告[11]中,提到三种“近期设备能力提高和加强”的技术,其中一种就是现代试验设计(MDOE)。该报告称:“MDOE试验设计方法在NASA兰利中心完成了演示,在耗费比常规试验方式更少费用和时间下,获得了更高质量的研究结果。这种试验方法和传统的单变量(OFAT)试验方式相比,具备显著降低风洞采集数据量的潜力,从而可以降低试验时间和成本”,“随着风洞再投资和设备的改造计划的实施(2001年春季开始),手动改变风洞运行模式的新增控制系统实现后,UPWT完整的MDOE试验功能将建设完成。”
经过十几年的发展,兰利研究中心已应用MDOE方法完成了100多项风洞试验[12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34],在如下方面的取得成果:1)减少试验周期和能耗[21, 35]。由于MODE试验不再以获得大量的试验数据为指导,而是以获得自变量与响应的规律(通过建模)为目的。在给定了响应模型的一定置信概率(如95%)下预测区间要求和风洞试验单点测量方差的条件下,可以计算出所需的最小数据量,而这个数据量通常要比传统的OFAT方法少一半左右;2)减小和量化数据不确定度[2, 10, 36, 37]。试验设备在使用中不可避免地会出现随时间的系统变化,如天平和支杆的杨氏模量随温度的改变、模型安装人员技能和疲劳程度、流场总温的改变以及测试设备的漂移等,这些变化对风洞数据系统误差的贡献往往很大,最终体现为不同风洞、同一风洞不同期和同一试验不同时间的系统误差。由于在传统的顺序试验方式中各点的误差是不具备统计独立性,所以在一次(期)试验中显现不完全,但其对于飞行器预测的误差贡献始终是存在的。MDOE试验执行过程采用了数据采集重复化、区块化和随机化的策略,使得测量误差具备统计独立性,能够减小和量化评估系统误差。
近年来国内在航空航天科研领域在气动布局研究、多目标优化方面逐渐开始应用现代试验设计[38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48],但国内风洞试验领域尚未见有关MDOE方法研究成果公开发表[49]。国内风洞鲜见采用MODE方法的主要原因有以下几点:1) 现有风洞设备是基于OFAT方法建设的,风洞设备开展MODE方法试验所需的改造较数值模拟研究领域更为复杂困难;2) OFAT方法的成熟性较高,试验人员掌握了丰富的基于OFAT方法的试验数据的处理和误差防范技能;3) 型号设计部门习惯进行单变量的任务提出和数据使用,而且具备处理可能出现误差的经验(如在进行攻角/侧滑角耦合试验中,对于弹性角导致的侧滑角偏离试验要求值的量,会要求风洞单位提供而不需修正);4) MDOE方法的复杂性和研究成果缺乏。相对于传统OFAT方法,MODE方法是基于多变量的试验技术进行的,涉及到了试验设计、回归建模、误差分析和风洞测控匹配等多个环节,其实现更为复杂,理论和实践研究比较欠缺。而风洞试验数据是型号制导控制气动性能数据库建立的基础,传统的OFAT方法研究充分,MDOE方法目前处于初步研究阶段,尚需进行研究和评估;5) 风洞试验人员对与MDOE方法熟悉和认可的程度较低,关注度不高。
2012年以来中国航天空气动力技术研究院开展了MDOE方法应用于风洞试验的研究。在FD-12亚跨超风洞中,分别用OFAT和MDOE两种方法对八号标模尾翼测力模型进行试验,比较研究两种方法的数据质量和成本消耗,本文将对研究方法和结果进行介绍。 1 研究对象
本文将MDOE方法应用于八号标模尾翼测力模型风洞试验。八号标模为小气动载荷导弹类外形标模,有国内外风洞的全弹和尾翼测力数据可供对比[50]。如图 1所示,该模型的具有四片尾翼,呈“X”字布局,其中尾翼1为被测量翼,安装在模型内部的专用天平上,测量其所受的空气动力和力矩载荷。试验马赫数Ma=0.6,侧滑角β= -5°、-3°、-2°、0°、2°、3°、5°,攻角α= -8°、-4°、0°、4°、6°、8°、10°、14°、18°、20°,舵偏角δ=-30°、-20°、-10°、0°、10°、20°、30°。
 |
| 图 1 风洞试验模型气动布局示意图(单位:mm)Fig. 1 Sketch of aerodynamic configuration of the wind tunnel model(unit:mm) |
FD-12风洞的试验段横截面尺寸为1.2m×1.2m,亚跨声速试验段的长度为3.8m,超声速试验段的长度为2.4m,试验马赫数范围为0.4~4.5。风洞的超扩段内有一套攻角机构,可实现攻角范围为-15°~25°,在攻角机构上配备有连续滚转角变化机构,滚转角变化范围为-180°~180°。 2 MDOE试验的设计
MDOE试验设计的输出是试验大纲,包括测量点的数量和自变量的取值。MDOE方法在同一次吹风试验中要同时对两个或两个以上的自变量进行改变。FD-12风洞具备同一次吹风连续改变攻角和滚转角的能力,利用风洞的滚转角/攻角耦合实现给定的攻角/侧滑角姿态,可以在同一次吹风中完成固定舵偏组合和马赫数下的所有侧滑角(-5°~5°)和攻角(-8°~20°)的组合姿态。所以,本试验中进行试验设计的自变量为攻角和侧滑角。 2.1 设计空间和响应模型
自变量的取值范围称为设计空间。试验中设计空间为攻角α= -8°~20°和侧滑角β=-5°~5°。MDOE试验方法通常采用响应面法(RSM,Response Surface Methods)进行建模。响应面模型是对自变量和响应之间变化规律的近似表示。通过建立响应面模型,飞行器设计人员不仅可以获得气动特性随单一自变量的变化规律,还可以得到多个自变量的耦合效应。
采用了基于多项式的响应面模型。在试验设计之初,根据已有的资料对该模型的气动特性进行了预估和分析。该模型在小攻角范围,气动力和力矩特性线性较好,而在大攻角范围,呈现出了较为明显的非线性特性。所以为了更好的建立模型,以攻角8°为界限将设计空间划分为两个子空间,分别称为小攻角子空间(α= -8°~8°;侧滑角β= -5°~5°)和大攻角子空间(α=8°~20°;侧滑角β= -5°~5°)。 2.2 测量点的数量和取值
测量点是吹风中要采集天平输出的攻角和侧滑角组合状态。测量点总数由响应面模型的阶次和试验的精准度要求决定。对于每个子空间,建立多项式响应面模型所需要的最小样本点数量等于这个多项式的项数,可以用下式(1)计算:
其中p为k元d次多项式的项数。本文用2元3次多项式响应面模型对子空间进行建模,即k=2,d=3,最小数据量为p=10。尽管p个数据点可以满足一个k元d次多项式响应面参数的确定,但要保证响应面模型的具备足够小的预测不确定度,还需增加一定量的重复点和校验点。在MDOE设计中增加一定量的重复点是很必要的,因为对于响应面模拟存在着一些对模型影响非常大的位置,这些位置的点会有杠杆效应,其误差会在整个模型中被放大。增加一定量的重复点可以消除杠杆效应,同时重复点也可以用于对试验精度的评估。要使得响应面预测值在平均95%置信概率水平下不与设计空间中任一点的测量结果出现显著差异,样本点总数n需要满足下式[13]:
对于本试验的一个子空间,数据空间只要达到17(n=1.625×10=16.25)就可以满足航空航天工程应用中通常能够接受的95%置信度约定。
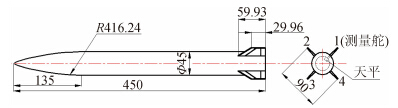
确定子空间数据点的数目后,需要选择合适的测量点取值,使拟合出的响应面模型有较好的预测准确性,这也就是取点的优化设计问题。本文采用了IV-最优化方法,这种方法是寻求设计空间的整体预测方差最小的设计,非常适合于精度要求较高的响应面模型的建立。小攻角子空间的设计结果如图 2所示,共有20个测点,其中包括5个重复点,点旁边的数字表示重复。
 |
| 图 2 攻角/侧滑角子空间的2元3阶IV-最优设计Fig. 2 α/β design space for two-factors three-order IV-optimal design |
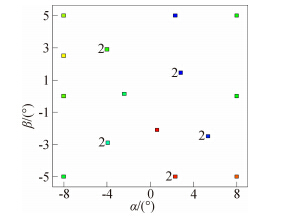
图 3对传统的OFAT方法和MDOE方法测量点在攻角-侧滑角设计空间中分布进行了比较。图 3(b)把大小攻角两个子空间进行了合并,由于在攻角α=8°的处有小攻角子空间有两点和大攻角子空间重复,所以对这四个点进行了合并。整个攻角-侧滑测量38个点。MDOE方法的测量点数量是OFAT方法的54.3%,而且还有可用于评估数据不确定度10个重复点(红色的点)。 角平面内,OFAT方法需要测量70个点,MDOE方法
 |
| 图 3 OFAT方法和MDOE方法测量点在攻角/ 侧滑角设计空间中分布对比图Fig. 3 Comparison of the points distribution of OFAT design and MDOE design |
MDOE试验设计完成的风洞运行大纲,是风洞执行过程的“输入”。风洞执行过程包括吹风、数据采集和处理,最终的输出是响应面模型。 3.1 风洞试验运行方式
MDOE试验中同一车次的攻角/侧滑角改变次序要遵循随机化原则。为了能够实现自变量改变次序的随机化,对风洞测控系统进行了一些修改。自变量非顺序改变使每个测量点的姿态角机构运行时间有所增加,但由于MDOE方法的测量点总数较少,最终其吹风的时间要比OFAT的少30%左右。 3.2 数据的获取
数据的采集方式和OFAT试验系统类似。当模型攻角和侧滑角到达给定位置,在气流稳定1s后,对气流参数和天平信号进行采集,采集到的数据保留至硬盘上。吹风停止后,通过计算天平公式,将天平电信号转换为载荷,然后对数据进行无量纲化处理,得到每个攻角-侧滑角状态下的气动力和力矩系数。对这些数据点采用最小二乘法进行拟合,完成响应面建模。
MODE试验中要对每次试验完成的数据的质量进行定量化评估,并据此决定是否获得本设计空间的充分信息并可进行下一个状态,最常用的就是对回归模型的方差分析(Analysis of Variance,ANOVA)。本试验采用F检验方法对响应面模型的拟合度进行检验。 4 试验数据分析 4.1 响应面模型的确定
每个设计子空间的任一个气动力系数都采用一个2元3次多项式表示。以舵面法向力系数为例,可表示为:
其中α、β分别为攻角和侧滑角,C00、C10、C01等为响应面方程的10个待定系数。MDOE方法和OFAT方法的一个重要差异是——MDOE方法能够使用方差分析等统计手段,评估和提高整个响应面模型的预测质量。图 4(a)给出了一个大攻角子空间的舵面法向力系数的初始响应曲面。表 1给出了响应面模型各项系数及其预测残差平方和判定系数R2。 初始响应面的R2是0.86468,失拟指标的F检验结果为显著。表 2给出方差分析结果,可以看出初始响应面的α3、α2β和αβ2等项的F统计量较小,可以去掉。对比几种不同的拟合结果后,最终选用了一个4阶响应面模型(如图 4(b)所示)。其系数在表 1中给出,预测判定系数R2 提高到了0.98473,失拟指标的F检验结果为不显 著。表 2中给出了最终响应面的F检验结果,可以看出各项系数的F统计量均较大。
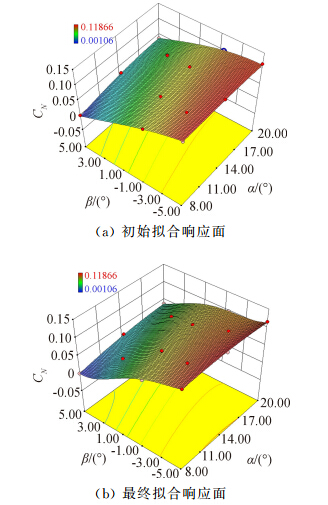 |
| 图 4 舵面法向力系数的响应曲面(Ma = 0.6,δ = 0°)Fig. 4 Response surface for the normal force coefficient of the vertical tail fin(Ma = 0.6,δ = 0°) |
| 初始响应面 | 最终响应面 | |
| 截距 | 2.9008×10-2 | 1.8067×10-2 |
| α | 5.1211×10-3 | 7.3775×10-3 |
| β | -1.8037×10-2 | -2.2153×10-2 |
| α β | 7.4635×10-4 | 8.3274×10-4 |
| α2 | -6.6143×10-5 | -1.7713×10-4 |
| β2 | -7.5194×10-5 | -8.5265×10-4 |
| α2β | -1.3042×10-5 | 0 |
| α β2 | -2.4208×10-5 | -3.5169×10-5 |
| α3 | -1.8111×10-6 | 0 |
| β3 | 4.0836×10-5 | 3.2763×10-4 |
| α β3 | 0 | -2.0504×10-5 |
| β4 | 0 | 3.3643×10-5 |
| 预测残差平方 | 1.9588×10-5 | 6.1346×10-6 |
| 预测判定系数R2 | 8.6468×10-1 | 9.8473×10-1 |
| 失拟是否显著 | 是 | 否 |
| F统计量(初始响应面) | F统计量(最终响应面) | |
| α | 11.4827 | 90.9730 |
| β | 162.9069 | 555.8944 |
| α β | 32.4445 | 42.1320 |
| α2 | 3.8098 | 17.6211 |
| β2 | 15.3698 | 20.3211 |
| α2β | 0.5132 | —— |
| α β2 | 0.7784 | 6.3115 |
| α3 | 0.0060 | —— |
| β3 | 1.1597 | 3.8971 |
| α β3 | —— | 13.4588 |
| β4 | —— | 10.1772 |
MDOE方法的优点是能够非常方便得到设计空间内任意攻角和侧滑角耦合的气动特性,即可以在自变量的设计空间内任意取值,而且还能够给出其置信区间,通过置信区间可以非常具体的掌握试验数据的分散度。图 5中的两条虚线之间的间隔是舵面法向力系数95%概率的置信区间,是对响应面模型截取剖面线得到的,单点给出了OFAT方式测量的对应数据。结果显示OFAT数据都在落在MDOE的预测区间之内。类似的,图 6和图 7给出了该测量舵的力矩系数Cm和Cl的比较曲线,对比结果与舵面法向力系数的类似。
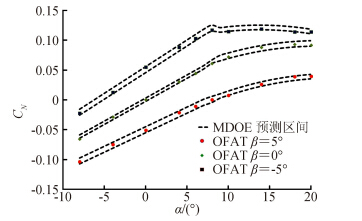 |
| 图 5 MDOE试验95%概率的预测区间和OFAT测量的 舵面法向力系数比较(Ma =0.6,δ=0°)Fig. 5 ResponseComparison of MDOE 95% prediction intervals and OFAT measured normal force coefficients of the vertical fin (Ma =0.6,δ=0°) |
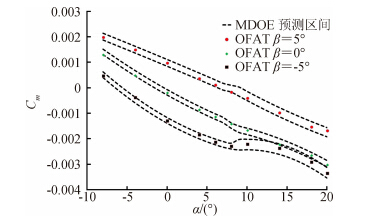 |
| 图 6 MDOE试验95%概率的预测区间和OFAT测量的 舵面铰链力矩系数比较(Ma =0.6,δ=0°)Fig. 6 Comparison of MDOE 95% prediction intervals and OFAT measured the hinge moment coefficients of the vertical fin (Ma =0.6,δ=0°) |
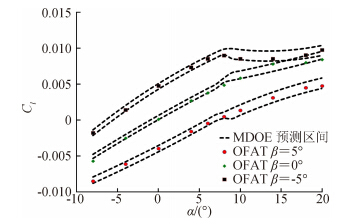 |
| 图 7 MDOE试验95%概率的预测区间和OFAT测量的 舵面滚转力矩系数比较(Ma =0.6,δ=0°)Fig. 7 Comparison of MDOE 95% prediction intervals and OFAT measured the rolling moment coefficients of the vertical fin (Ma =0.6,δ=0°) |
MDOE试验中重复点所占比重较大。如本试验的38个点中有10个重复点,重复率为36%。重复点可以提高响应面模型的预测精准度,也用于对试验不确定度的计算。在OFAT试验中,这样详尽的误差分析试验很难开展,通常一期试验中选择个别典型状态进行7次重复性试验,将计算出的均方根误差作为全部试验数据的误差,其准确性不高。为了从总体上评估试验不确定度,表 3给了该测量舵CN、Cm和Cl的6个响应面模型95%概率的置信区间半宽度,这是通过对残差平方的平均值取平方根再乘以2倍算得的。
| Residual mean square | 95%半区间 | |||
| 小攻角子空间 | 大攻角子空间 | 小攻角子空间 | 大攻角子空间 | |
| CN | 1.9657×10-5 | 6.13457×10-6 | 8.867317×10-3 | 4.953614×10-3 |
| Cm | 5.4108×10-9 | 1.88324×10-8 | 1.47116×10-4 | 2.74463×10-4 |
| Cl | 1.0388×10-7 | 2.42263×10-7 | 6.44593×10-4 | 9.84404×10-4 |
本文在FD-12风洞开展了MODE风洞试验方法的研究。以八号标模为研究对象,完成了MDOE舵面测力试验。研究内容包括MDOE设计、试验执行和数据分析处理等过程,对MDOE试验方法在获取试验信息、提高数据精准度、降低成本和缩短试验周期等方面进行了分析。主要结论如下:
(1) MDOE方法获得的数据和作为对比的OFAT 方法获得的数据规律一致,吻合很好。
(2) MDOE风洞对每个状态采集38个点,对应的OFAT需要70个,MDOE采集样点数减少了46%,吹风的时间比OFAT减少30%左右,提高了风洞试验效率,缩短了试验周期。
(3) 试验中每个状态的38个点中有10个是重复点,重复率为36%,能够给出设计空间内任意攻角/侧滑角耦合状态的气动参数的置信区间。
(4) MDOE试验结果通过响应面模型表达,能够直接获得设计空间内任意自变量组合的响应值,避免了数据使用时的插值误差。
风洞试验是一项高能耗的科研工作,MDOE风洞试验方法更能够推动风洞试验的低碳化发展,符合我国当今大力建设生态文明的精神。在国外MDOE方法正越来越多地应用于风洞试验领域的各个方面,包括风洞试验、气动布局研究、模型设计优化、数据库建设、天平校准、计算模拟等方面。人们对MDOE方法的认识逐步提高,用MDOE方法的理念处理空气动力试验研究领域问题正在被越来越多的人接受。MDOE方法是一种科学的方法,是风洞试验方法的一次革命,代表风洞试验方法发展方向,应开展更多的MDOE风洞试验方法的研究工作。
| [1] | DeLoach R, Micol J R. Analysis of wind tunnel polar replicates using the modern design of experiments (invited)[R]. AIAA 2010-4927. 27th AIAA Aerodynamic Measurement Technology and Ground Testing Conference. Chicago, I L, 2010. |
| [2] | DeLoach R. Tactical defenses against systematic variation in wind tunnel testing[R]. AIAA 2002-0540. 40th AIAA Aerospace Sciences Meeting and Exhibit. Reno, Nevada, 2002. |
| [3] | DeLoach R, Obara C J, Goodman W. A practical methodology for quantifying the random and systematic components of unexplained variance in wind tunnel data[R]. AIAA 2012-0764. 50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Nashville, Tennessee, 2012. |
| [4] | DeLoach R. Propagation of computational uncertainty using the modern design of experiments[R]. Hampton, Virginia: Langley Research Center, 2007. |
| [5] | DeLoach R. Applications of modern experiment design to wind tunnel testing at NASA Langley Research Center[R]. AIAA 98-0713. 36th AIAA Aerospace Sciences Meeting and Exhibit. Reno, NV, 1998. |
| [6] | Fisher R A. The design of experiments[M]. Oliver and Boyd, Edinburgh, 1935. |
| [7] | Fisher R A. Statistical methods for research workers[M]. Oliver and Boyd, Edinburgh, 1925. |
| [8] | Fisher R A. Statistical Methods and Scientific Inference[M]. Oliver and Boyd, Edinburgh, 1956. |
| [9] | DeLoach R. Analysis of variance in the modern design of experiments[R]. AIAA 2010-1111. 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Orlando, Florida, 2010. |
| [10] | DeLoach R. Improved quality in aerospace testing through the modern design of experiments[R]. AIAA 2000-0825. 38th AIAA Aerospace Sciences Meeting and Exhibit. Reno, Nevada, 2000. |
| [11] | John R, Micol J R. NASA Langley Langley Research Center's unitary plan wind tunnel: testing capabilities and recent modernization activities research center[R]. AIAA 2001-0456. 39th AIAA Aerospace Sciences Meeting and Exhibit, 2001. |
| [12] | DeLoach R, Marlowe J M, Yager T J. Uncertainty analysis for the evaluation of a passive runway arresting system[R]. AIAA 2009-1156. 47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Orlando, Florida, 2009. |
| [13] | DeLoach R, Micol J R. Comparison of resource requirements for a wind tunnel test designed with conventional vs. modern design of experiments methods[R]. AIAA 2011-1260. 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. Orlando, Florida, 2011. |
| [14] | DeLoach R. The modern design of experiments for configuration aerodynamics: a case study[R]. AIAA 2006-923. 44th AIAA Aerospace Sciences Meeting and Exhibit. Reno, NV, 2006. |
| [15] | DeLoach R, Rayos E M, Campbell C H, et al. Space shuttle debris impact tool assessment using the modern design of experiments[R]. AIAA 2007-550. 45th AIAA Aerospace Sciences Meeting and Exhibit. Reno, NV, 2007. |
| [16] | Erickson G E, DeLoach R. Estimation of supersonic stage separation aerodynamics of winged-body launch vehicles using response surface methods[R]. Hampton, Virginia: Langley Research Center, 2010. |
| [17] | Dowgwillo R M, DeLoach R. Using modern design of experiments to create a surface pressure database from a low speed wind tunnel test[R]. AIAA 2004-2200. 24th AIAA Aerodynamic Measurement Technology and Ground Testing Conference. Portland, Oregon, 2004. |
| [18] | Danehy P M, DeLoach R, Cutler A D. Application of modern design of experiments to CARS thermometry in a supersonic combustor[R]. AIAA 2002-2914. 22nd AIAA Aerodynamic Measurement Technology and Ground Testing Conference. St. Louis, Missouri, 2002. |
| [19] | Lo C F, Zhao J L, DcLoach R. Application of neural networks to wind tunnel data response surface methods[R]. AIAA 2000-2639. 21st AIAA Aerodynamic Measurement Technology and Ground Testing Conference. Denver, CO., 2000. |
| [20] | Dominguez K, Graham A B. Development of an MDOE compliant control system in the VIGYAN low-speed wind tunnel[R]. AIAA 2001-0169. 39th AIAA Aerospace Sciences Meeting and Exhibit. Reno, Nevada, 2001 |
| [21] | DeLoach R, Cler D L, Graham A B. Fractional factorial experiment designs to minimize configuration changes in wind tunnel testing[R]. AIAA 2002-0746. 40th AIAA Aerospace Sciences Meeting and Exhibit. Reno, Nevada, 2002. |
| [22] | DeLoach R. The modern design of experiments-a technical and marketing framework[R]. AIAA 2000-2691. 21st AIAA Advanced Measurement Technology and Ground Testing Conference. Denver, CO., 2000. |
| [23] | DeLoach R. The role of hierarchy in response surface modeling of wind tunnel data[R]. AIAA 2010-0931. 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Orlando, Florida, 2010. |
| [24] | DeLoach R, Ulbrich N. A comparison of two balance calibration model building methods[R]. AIAA 2007-0147. 45th AIAA Aerospace Sciences Meeting and Exhibit. Reno, NV, 2007. |
| [25] | DeLoach R. Assessment of response surface models using independent confirmation point analysis[R]. AIAA 2010-0741. 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Orlando, Florida, 2010. |
| [26] | DeLoach R. Bayesian inference in the modern design of experiments[R]. AIAA 2008-0847. 46th AIAA Aerospace Sciences Meeting and Exhibit. Reno, Nevada, 2008. |
| [27] | DeLoach R, Philipsen I. Stepwise regression analysis of MDOE balance calibration data acquired at DNW[R]. AIAA 2007-144. 45th AIAA Aerospace Sciences Meeting and Exhibit. Reno, NV, 2007. |
| [28] | Underwood P J. National transonic facility wall pressure calibration using modern design of experiments (Invited)[R]. AIAA 2001-0171. 39th AIAA Aerospace Sciences Meeting and Exhibit. Reno, Nevada, 2001. |
| [29] | Danehy P M, Dorrington A A, Cutler A D, DeLoach R. Response surface methods for spatially-Resolved optical measurement techniques(invited)[R]. AIAA 2003-0648. 41st AIAA Aerospace Sciences Meeting and Exhibit. Reno, Nevada, 2003. |
| [30] | Morelli E A, DeLoach R. Response surface modeling using multivariate orthogonal functions[R]. AIAA 2001-0168. 39th AIAA Aerospace Sciences Meeting and Exhibit. Reno, Nevada, 2001. |
| [31] | Parker P A, DeLoach R. Structural optimization of a force balance using a computational experiment design(invited)[R]. AIAA 2002-0540. 40th AIAA Aerospace Sciences Meeting and Exhibit. Reno, Nevada, 2002. |
| [32] | Burner A W, Tianshu Liu, DeLoach. R. Uncertainty of videogrammetric techniques used for aerodynamic testing[R]. AIAA 2002-2794. 22nd AIAA Aerodynamic Measurement Technology and Ground Testing Conference. St. Louis, Missouri, 2002. |
| [33] | Morelli E A, DeLoach R. Wind tunnel database development using modern experiment design and multivariate orthogonal functions[R]. AIAA 2003-0653. 41th AIAA Aerospace Sciences Meeting and Exhibit. Reno, Nevada, 2003. |
| [34] | Rhode M N, DeLoach R. Hypersonic wind tunnel calibration usingthe modern design of experiments[R]. AIAA 2005-4274. 41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit. Tucson, AZ, 2005. |
| [35] | DeLoach R. Tailoring wind tunnel data volume requirements through the formal design of experiments[R]. AIAA 1998-2884. 20th AIAA Advanced Measurement and Ground Testing Technology Conference. Albuquerque, N M, 1998. |
| [36] | DeLoach R, Hill J S, Tomek W G. Practical applications of response surface methods in the national transonic facility (invited)[R]. AIAA 2001-0167. 39th AIAA Aerospace Sciences Meeting and Exhibit. Reno, N V, 2001. |
| [37] | DeLoach R. Blocking: a defense against long-period unexplained variance in aerospace ground testing (invited)[R]. AIAA 2003-0650. 41st AIAA Aerospace Sciences Meeting & Exhibit. Reno, N V, 2003. |
| [38] | Gu Xingruo. The future of balance concluded from the first international conference on contingency balance[J]. Experiments and Measurements in Fluid Mechanics, 1997, 11(1): 24-26. (in Chinese) 顾兴若. 从“首届应变天平国际会议”看天平技术的发展动向[J]. 流体力学实验与测量, 1997, 11(1): 24-26. |
| [39] | Su Jianmin, Song Bifeng, Yin Qing,et al. Joined/tandem wing aircraft focus calculation study based on response surface method[J]. Journal of Nanchang Hangkong University(Natural Science), 2008, 22(1): 35-39. (in Chinese) 苏建民, 宋笔锋, 尹清, 等. 二次响应面联/排翼布局飞机焦点计算[J]. 南昌航空大学学报(自然科学版), 2008, 22(1): 35-39. |
| [40] | Xing Bida, Gong Guanghong, Li Ni,et al. Research of missile MDO methods based on multi-granularity model[J]. Journal of System Simulation, 2010, 22(11): 2639-2645. (in Chinese) 邢必达, 龚光红, 李妮, 等. 基于多粒度模型的导弹MDO方法研究[J]. 系统仿真学报, 2010, 22(11): 2639-2645. |
| [41] | Peng Jianglong. Radio network parameters adjustment based on DOE[J]. Telecom Engineering Technics and Standardization, 2012, (1): 16-21. (in Chinese) 彭江龙. 基于试验设计(DOE)方法的无线网络参数设置[J]. 电信工程技术与标准化, 2012, (1): 16-21. |
| [42] | Ma Ying, He Linshu, Duan Yong. Conceptual design of cruise missile based on technology of modern design of experiment[J]. Journal of Beijing University of Aeronautics and Astronautics, 2008, 34(10): 1121-1125. (in Chinese) 马英, 何麟书, 段勇. 基于现代实验设计技术的巡航导弹概念设计[J]. 北京航空航天大学学报, 2008, 34(10): 1121-1125. |
| [43] | Deng Lei, Qiao Zhide, Song Wenping,et al. Multi-objective aerodynamic optimization design of wind turbine blade based on response surface methodology[J]. Acta Aerodynamica Sinica, 2012, 30(3): 405-410. (in Chinese) 邓磊, 乔志德, 宋文萍, 等. 基于响应面方法的风力机叶片多目标优化设计研究[J]. 空气动力学学报, 2012, 30(3): 405-410. |
| [44] | Gao Guanglin, Song Bifeng, Wang Liguang,et al. Study of opening holes on the wing of flapping-wing MAV and its effect on aerodynamic characteristic[J]. Journal of Experiments in Fluid Mechanics, 2010, 24(5): 70-73. (in Chinese) 高广林, 宋笔锋, 王利光, 等. 扑翼飞行器机翼开孔对气动特性的影响研究[J]. 实验流体力学, 2010, 24(5): 70-73. |
| [45] | Yan Xiaodong, Han Bing. Application of experiment design method in performancesimulation validation for flight vehicle[J]. Flight Dynamics, 2012, 30(1): 79-82. (in Chinese) 闫晓东, 韩冰. 试验设计方法在飞行器性能仿真验证中的应用[J]. 飞行力学, 2012, 30(1): 79-82. |
| [46] | Zhang Zezhi, Han Chunliang, Li Chengwei. Application of response surface method in experimental design and optimization[J]. Journal of Henan Institute of Education(Natural Science Edition), 2011, 20(4): 34-37. (in Chinese) 张泽志, 韩春亮, 李成未. 响应面法在试验设计与优化中的应用[J]. 河南教育学院学报(自然科学版), 2011, 20(4): 34-37. |
| [47] | Cheng Xingqun, Yu Jingping. Application of orthogonal design method to aerodynamic character research on coach external flow field[J]. Bus & Coach Technology and Research, 2012, (4): 17-19. (in Chinese) 程兴群, 于敬平. 正交试验设计在客车外围流场空气动力学特性研究中的应用[J]. 客车技术与研究, 2012, (4): 17-19. |
| [48] | Zhan Peiguo. Study on wind tunnel balance calibration standard of AIAA[J]. Aeronautical Science & Technology, 2012, (3): 24-26. (in Chinese) 战培国. AIAA风洞天平校准标准研究[J]. 航空科学技术, 2012, (3): 24-26. |
| [49] | Zhan Peiguo. Review of modern design of experiment methods in wind tunnel test[J]. Aeronautical Science and Technology, 2011, (6): 11-14. (in Chinese) 战培国. MDOE风洞试验方法研究[J]. 航空科学技术, 2011, (6): 11-14. |
| [50] | Jimmie N Derrick, Donald J Spring, Gary C. Aerodynamic characteristics of a series of bodies with and without tails at Mach numbers from 0.8 to 3.0 and angles of attack from 0 to 45 degrees[R]. ADA 028324, 1976." |